CSOUND
RANDOM
This chapter is in three parts. Part I provides a general introduction to the concepts behind random numbers and how to work with them in Csound. Part II focusses on a more mathematical approach. Part III introduces a number of opcodes for generating random numbers, functions and distributions and demonstrates their use in musical examples.
I. GENERAL INTRODUCTION
Random is Different
The term random derives from the idea of a horse that is running so fast it becomes 'out of control' or 'beyond predictability'.1 Yet there are different ways in which to run fast and to be out of control; therefore there are different types of randomness.
We can divide types of randomness into two classes. The first contains random events that are independent of previous events. The most common example for this is throwing a die. Even if you have just thrown three '1's in a row, when thrown again, a '1' has the same probability as before (and as any other number). The second class of random number involves random events which depend in some way upon previous numbers or states. Examples here are Markov chains and random walks.
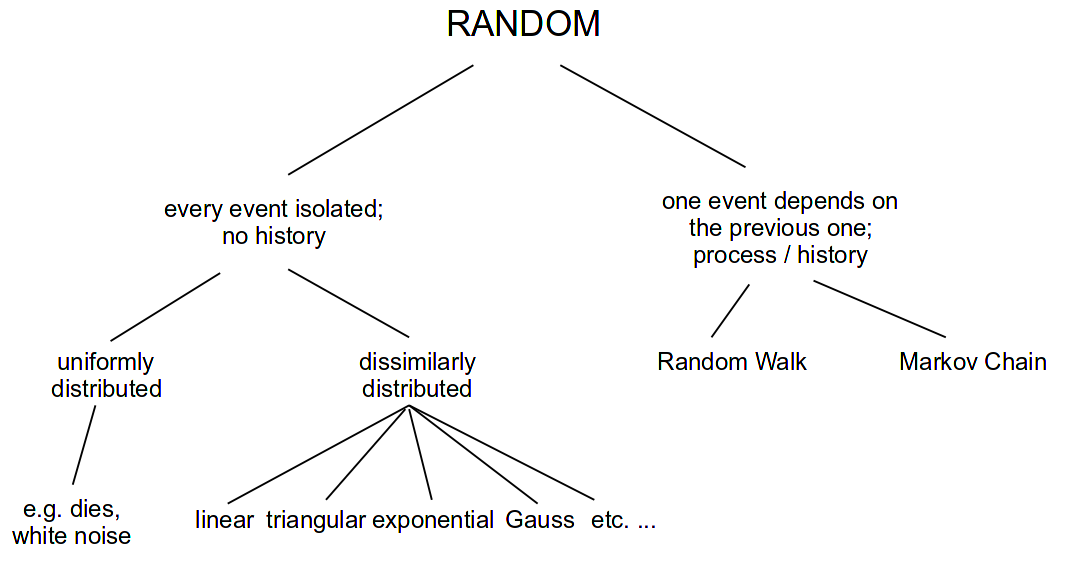
The use of randomness in electronic music is widespread. In this chapter, we shall try to explain how the different random horses are moving, and how you can create and modify them on your own. Moreover, there are many pre-built random opcodes in Csound which can be used out of the box (see the overview in the Csound Manual). The final section of this chapter introduces some musically interesting applications of them.
Random Without History
A computer is typically only capable of computation. Computations are deterministic processes: one input will always generate the same output, but a random event is not predictable. To generate something which looks like a random event, the computer uses a pseudo-random generator.
The pseudo-random generator takes one number as input, and generates another number as output. This output is then the input for the next generation. For a huge amount of numbers, they look as if they are randomly distributed, although everything depends on the first input: the seed. For one given seed, the next values can be predicted.
Uniform Distribution
The output of a classical pseudo-random generator is uniformly distributed: each value in a given range has the same likelihood of occurence. The first example shows the influence of a fixed seed (using the same chain of numbers and beginning from the same location in the chain each time) in contrast to a seed being taken from the system clock (the usual way of imitating unpredictability). The first three groups of four notes will always be the same because of the use of the same seed whereas the last three groups should always have a different pitch.
EXAMPLE 01D01_different_seed.csd
<CsoundSynthesizer>
<CsOptions>
-d -odac -m0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr generate
;get seed: 0 = seeding from system clock
; otherwise = fixed seed
seed p4
;generate four notes to be played from subinstrument
iNoteCount = 0
until iNoteCount == 4 do
iFreq random 400, 800
event_i "i", "play", iNoteCount, 2, iFreq
iNoteCount += 1 ;increase note count
enduntil
endin
instr play
iFreq = p4
print iFreq
aImp mpulse .5, p3
aMode mode aImp, iFreq, 1000
aEnv linen aMode, 0.01, p3, p3-0.01
outs aEnv, aEnv
endin
</CsInstruments>
<CsScore>
;repeat three times with fixed seed
r 3
i "generate" 0 2 1
;repeat three times with seed from the system clock
r 3
i "generate" 0 1 0
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Note that a pseudo-random generator will repeat its series of numbers after as many steps as are given by the size of the generator. If a 16-bit number is generated, the series will be repeated after 65536 steps. If you listen carefully to the following example, you will hear a repetition in the structure of the white noise (which is the result of uniformly distributed amplitudes) after about 1.5 seconds in the first note.2 In the second note, there is no perceivable repetition as the random generator now works with a 31-bit number.
EXAMPLE 01D02_white_noises.csd
<CsoundSynthesizer>
<CsOptions>
-d -odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr white_noise
iBit = p4 ;0 = 16 bit, 1 = 31 bit
;input of rand: amplitude, fixed seed (0.5), bit size
aNoise rand .1, 0.5, iBit
outs aNoise, aNoise
endin
</CsInstruments>
<CsScore>
i "white_noise" 0 10 0
i "white_noise" 11 10 1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Two more general notes about this:
- The way to set the seed differs from opcode to opcode. There are several opcodes such as rand featured above, which offer the choice of setting a seed as input parameter. For others, such as the frequently used random family, the seed can only be set globally via the seed statement. This is usually done in the header so a typical statement would be:
<CsInstruments> sr = 44100 ksmps = 32 nchnls = 2 0dbfs = 1 seed = 0 ;seeding from current time
...
- Random number generation in Csound can be done at any rate. The type of the output variable tells you whether you are generating random values at i-, k- or a-rate. Many random opcodes can work at all these rates, for instance random:
1) ires random imin, imax 2) kres random kmin, kmax 3) ares random kmin, kmax
In the first case, a random value is generated only once, when an instrument is called, at initialisation. The generated value is then stored in the variable ires. In the second case, a random value is generated at each k-cycle, and stored in kres. In the third case, in each k-cycle as many random values are stored as the audio vector has in size, and stored in the variable ares. Have a look at example 03A16_Random_at_ika.csd to see this at work. Chapter 03A tries to explain the background of the different rates in depth, and how to work with them.
Other Distributions
The uniform distribution is the one each computer can output via its pseudo-random generator. But there are many situations you will not want a uniformly distributed random, but any other shape. Some of these shapes are quite common, but you can actually build your own shapes quite easily in Csound. The next examples demonstrate how to do this. They are based on the chapter in Dodge/Jerse3 which also served as a model for many random number generator opcodes in Csound.4
Linear
A linear distribution means that either lower or higher values in a given range are more likely:
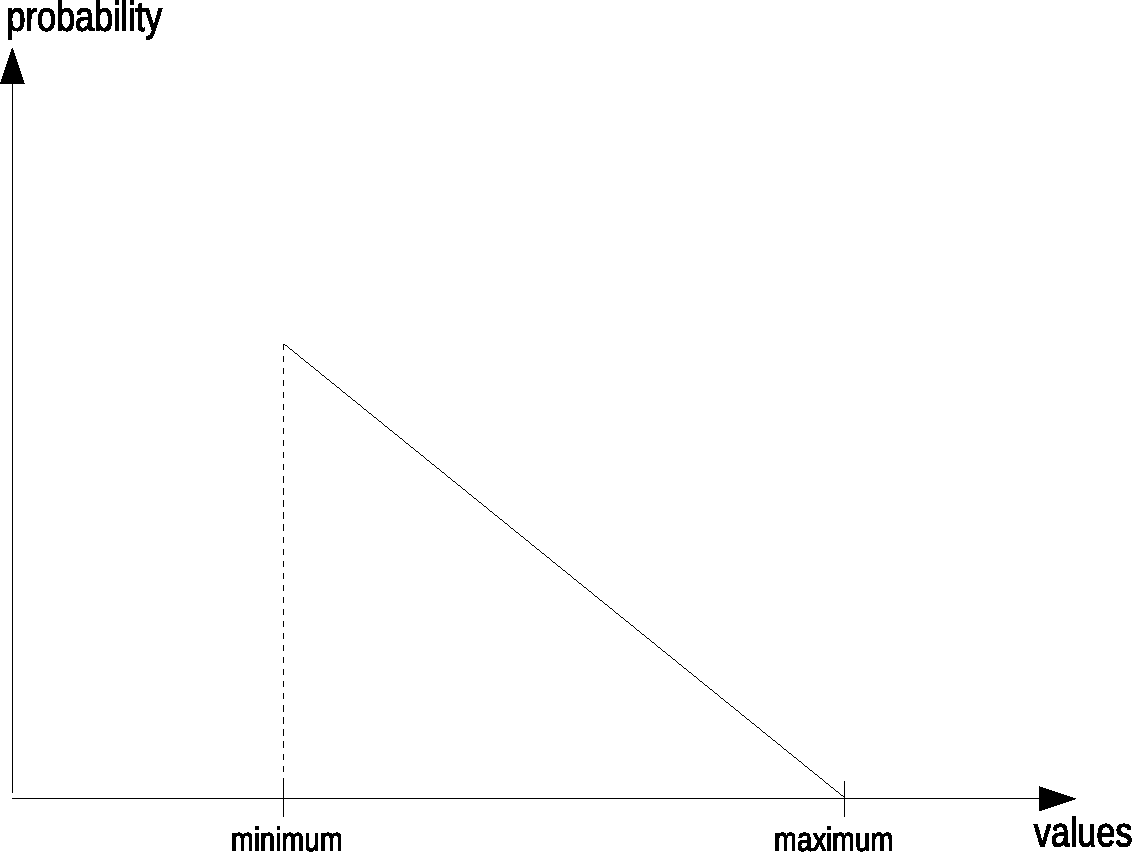
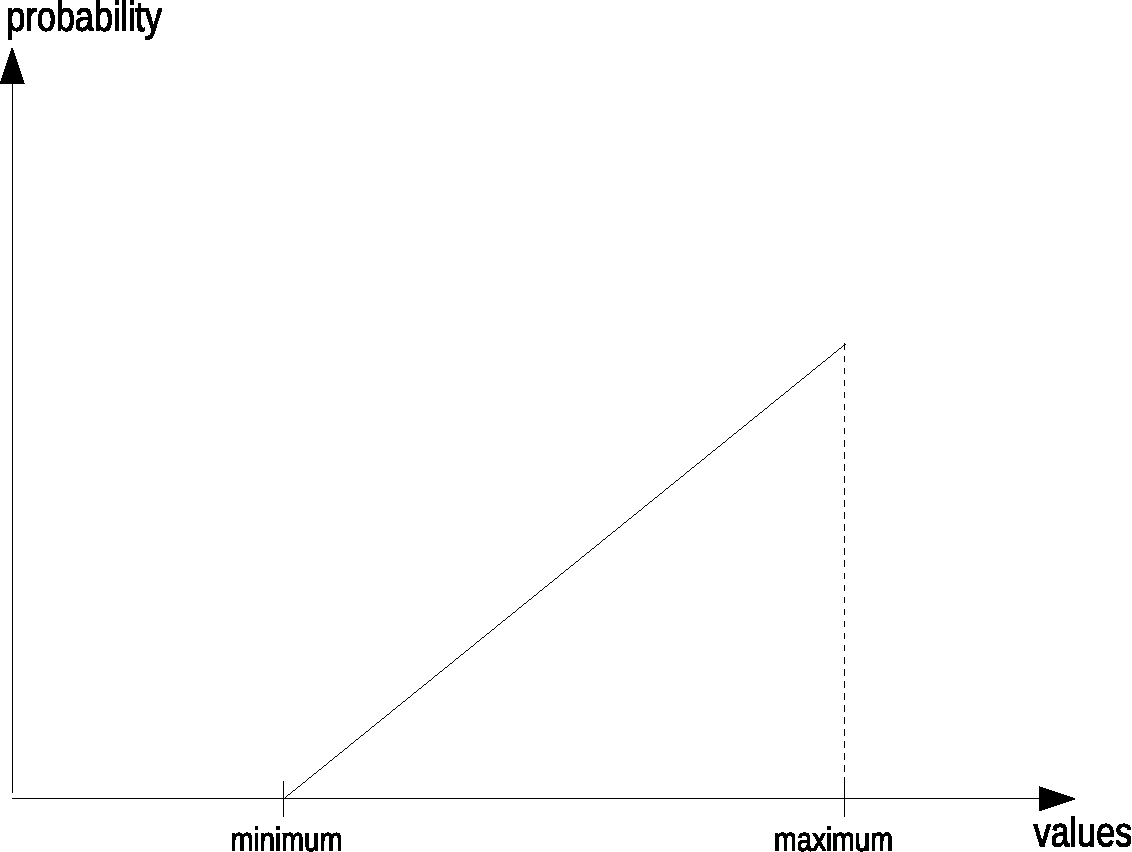
To get this behaviour, two uniform random numbers are generated, and the lower is taken for the first shape. If the second shape with the precedence of higher values is needed, the higher one of the two generated numbers is taken. The next example implements these random generators as User Defined Opcodes. First we hear a uniform distribution, then a linear distribution with precedence of lower pitches (but longer durations), at least a linear distribution with precedence of higher pitches (but shorter durations).
EXAMPLE 01D03_linrand.csd
<CsoundSynthesizer>
<CsOptions>
-d -odac -m0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0
;****DEFINE OPCODES FOR LINEAR DISTRIBUTION****
opcode linrnd_low, i, ii
;linear random with precedence of lower values
iMin, iMax xin
;generate two random values with the random opcode
iOne random iMin, iMax
iTwo random iMin, iMax
;compare and get the lower one
iRnd = iOne < iTwo ? iOne : iTwo
xout iRnd
endop
opcode linrnd_high, i, ii
;linear random with precedence of higher values
iMin, iMax xin
;generate two random values with the random opcode
iOne random iMin, iMax
iTwo random iMin, iMax
;compare and get the higher one
iRnd = iOne > iTwo ? iOne : iTwo
xout iRnd
endop
;****INSTRUMENTS FOR THE DIFFERENT DISTRIBUTIONS****
instr notes_uniform
prints "... instr notes_uniform playing:\n"
prints "EQUAL LIKELINESS OF ALL PITCHES AND DURATIONS\n"
;how many notes to be played
iHowMany = p4
;trigger as many instances of instr play as needed
iThisNote = 0
iStart = 0
until iThisNote == iHowMany do
iMidiPch random 36, 84 ;midi note
iDur random .5, 1 ;duration
event_i "i", "play", iStart, iDur, int(iMidiPch)
iStart += iDur ;increase start
iThisNote += 1 ;increase counter
enduntil
;reset the duration of this instr to make all events happen
p3 = iStart + 2
;trigger next instrument two seconds after the last note
event_i "i", "notes_linrnd_low", p3, 1, iHowMany
endin
instr notes_linrnd_low
prints "... instr notes_linrnd_low playing:\n"
prints "LOWER NOTES AND LONGER DURATIONS PREFERRED\n"
iHowMany = p4
iThisNote = 0
iStart = 0
until iThisNote == iHowMany do
iMidiPch linrnd_low 36, 84 ;lower pitches preferred
iDur linrnd_high .5, 1 ;longer durations preferred
event_i "i", "play", iStart, iDur, int(iMidiPch)
iStart += iDur
iThisNote += 1
enduntil
;reset the duration of this instr to make all events happen
p3 = iStart + 2
;trigger next instrument two seconds after the last note
event_i "i", "notes_linrnd_high", p3, 1, iHowMany
endin
instr notes_linrnd_high
prints "... instr notes_linrnd_high playing:\n"
prints "HIGHER NOTES AND SHORTER DURATIONS PREFERRED\n"
iHowMany = p4
iThisNote = 0
iStart = 0
until iThisNote == iHowMany do
iMidiPch linrnd_high 36, 84 ;higher pitches preferred
iDur linrnd_low .3, 1.2 ;shorter durations preferred
event_i "i", "play", iStart, iDur, int(iMidiPch)
iStart += iDur
iThisNote += 1
enduntil
;reset the duration of this instr to make all events happen
p3 = iStart + 2
;call instr to exit csound
event_i "i", "exit", p3+1, 1
endin
;****INSTRUMENTS TO PLAY THE SOUNDS AND TO EXIT CSOUND****
instr play
;increase duration in random range
iDur random p3, p3*1.5
p3 = iDur
;get midi note and convert to frequency
iMidiNote = p4
iFreq cpsmidinn iMidiNote
;generate note with karplus-strong algorithm
aPluck pluck .2, iFreq, iFreq, 0, 1
aPluck linen aPluck, 0, p3, p3
;filter
aFilter mode aPluck, iFreq, .1
;mix aPluck and aFilter according to MidiNote
;(high notes will be filtered more)
aMix ntrpol aPluck, aFilter, iMidiNote, 36, 84
;panning also according to MidiNote
;(low = left, high = right)
iPan = (iMidiNote-36) / 48
aL, aR pan2 aMix, iPan
outs aL, aR
endin
instr exit
exitnow
endin
</CsInstruments>
<CsScore>
i "notes_uniform" 0 1 23 ;set number of notes per instr here
;instruments linrnd_low and linrnd_high are triggered automatically
e 99999 ;make possible to perform long (exit will be automatically)
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Triangular
In a triangular distribution the values in the middle of the given range are more likely than those at the borders. The probability transition between the middle and the extrema are linear:

The algorithm for getting this distribution is very simple as well. Generate two uniform random numbers and take the mean of them. The next example shows the difference between uniform and triangular distribution in the same environment as the previous example.
EXAMPLE 01D04_trirand.csd
<CsoundSynthesizer>
<CsOptions>
-d -odac -m0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0
;****UDO FOR TRIANGULAR DISTRIBUTION****
opcode trirnd, i, ii
iMin, iMax xin
;generate two random values with the random opcode
iOne random iMin, iMax
iTwo random iMin, iMax
;get the mean and output
iRnd = (iOne+iTwo) / 2
xout iRnd
endop
;****INSTRUMENTS FOR UNIFORM AND TRIANGULAR DISTRIBUTION****
instr notes_uniform
prints "... instr notes_uniform playing:\n"
prints "EQUAL LIKELINESS OF ALL PITCHES AND DURATIONS\n"
;how many notes to be played
iHowMany = p4
;trigger as many instances of instr play as needed
iThisNote = 0
iStart = 0
until iThisNote == iHowMany do
iMidiPch random 36, 84 ;midi note
iDur random .25, 1.75 ;duration
event_i "i", "play", iStart, iDur, int(iMidiPch)
iStart += iDur ;increase start
iThisNote += 1 ;increase counter
enduntil
;reset the duration of this instr to make all events happen
p3 = iStart + 2
;trigger next instrument two seconds after the last note
event_i "i", "notes_trirnd", p3, 1, iHowMany
endin
instr notes_trirnd
prints "... instr notes_trirnd playing:\n"
prints "MEDIUM NOTES AND DURATIONS PREFERRED\n"
iHowMany = p4
iThisNote = 0
iStart = 0
until iThisNote == iHowMany do
iMidiPch trirnd 36, 84 ;medium pitches preferred
iDur trirnd .25, 1.75 ;medium durations preferred
event_i "i", "play", iStart, iDur, int(iMidiPch)
iStart += iDur
iThisNote += 1
enduntil
;reset the duration of this instr to make all events happen
p3 = iStart + 2
;call instr to exit csound
event_i "i", "exit", p3+1, 1
endin
;****INSTRUMENTS TO PLAY THE SOUNDS AND EXIT CSOUND****
instr play
;increase duration in random range
iDur random p3, p3*1.5
p3 = iDur
;get midi note and convert to frequency
iMidiNote = p4
iFreq cpsmidinn iMidiNote
;generate note with karplus-strong algorithm
aPluck pluck .2, iFreq, iFreq, 0, 1
aPluck linen aPluck, 0, p3, p3
;filter
aFilter mode aPluck, iFreq, .1
;mix aPluck and aFilter according to MidiNote
;(high notes will be filtered more)
aMix ntrpol aPluck, aFilter, iMidiNote, 36, 84
;panning also according to MidiNote
;(low = left, high = right)
iPan = (iMidiNote-36) / 48
aL, aR pan2 aMix, iPan
outs aL, aR
endin
instr exit
exitnow
endin
</CsInstruments>
<CsScore>
i "notes_uniform" 0 1 23 ;set number of notes per instr here
;instr trirnd will be triggered automatically
e 99999 ;make possible to perform long (exit will be automatically)
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
More Linear and Triangular
Having written this with some very simple UDOs, it is easy to emphasise the probability peaks of the distributions by generating more than two random numbers. If you generate three numbers and choose the smallest of them, you will get many more numbers near the minimum in total for the linear distribution. If you generate three random numbers and take the mean of them, you will end up with more numbers near the middle in total for the triangular distribution.
If we want to write UDOs with a flexible number of sub-generated numbers, we have to write the code in a slightly different way. Instead of having one line of code for each random generator, we will use a loop, which calls the generator as many times as we wish to have units. A variable will store the results of the accumulation. Re-writing the above code for the UDO trirnd would lead to this formulation:
opcode trirnd, i, ii
iMin, iMax xin
;set a counter and a maximum count
iCount = 0
iMaxCount = 2
;set the accumulator to zero as initial value
iAccum = 0
;perform loop and accumulate
until iCount == iMaxCount do
iUniRnd random iMin, iMax
iAccum += iUniRnd
iCount += 1
enduntil
;get the mean and output
iRnd = iAccum / 2
xout iRnd
endop
To get this completely flexible, you only have to get iMaxCount as input argument. The code for the linear distribution UDOs is quite similar. -- The next example shows these steps:
- Uniform distribution.
- Linear distribution with the precedence of lower pitches and longer durations, generated with two units.
- The same but with four units.
- Linear distribution with the precedence of higher pitches and shorter durations, generated with two units.
- The same but with four units.
- Triangular distribution with the precedence of both medium pitches and durations, generated with two units.
- The same but with six units.
Rather than using different instruments for the different distributions, the next example combines all possibilities in one single instrument. Inside the loop which generates as many notes as desired by the iHowMany argument, an if-branch calculates the pitch and duration of one note depending on the distribution type and the number of sub-units used. The whole sequence (which type first, which next, etc) is stored in the global array giSequence. Each instance of instrument "notes" increases the pointer giSeqIndx, so that for the next run the next element in the array is being read. If the pointer has reached the end of the array, the instrument which exits Csound is called instead of a new instance of "notes".
EXAMPLE 01D05_more_lin_tri_units.csd
<CsoundSynthesizer>
<CsOptions>
-d -odac -m0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0
;****SEQUENCE OF UNITS AS ARRAY****/
giSequence[] array 0, 1.2, 1.4, 2.2, 2.4, 3.2, 3.6
giSeqIndx = 0 ;startindex
;****UDO DEFINITIONS****
opcode linrnd_low, i, iii
;linear random with precedence of lower values
iMin, iMax, iMaxCount xin
;set counter and initial (absurd) result
iCount = 0
iRnd = iMax
;loop and reset iRnd
until iCount == iMaxCount do
iUniRnd random iMin, iMax
iRnd = iUniRnd < iRnd ? iUniRnd : iRnd
iCount += 1
enduntil
xout iRnd
endop
opcode linrnd_high, i, iii
;linear random with precedence of higher values
iMin, iMax, iMaxCount xin
;set counter and initial (absurd) result
iCount = 0
iRnd = iMin
;loop and reset iRnd
until iCount == iMaxCount do
iUniRnd random iMin, iMax
iRnd = iUniRnd > iRnd ? iUniRnd : iRnd
iCount += 1
enduntil
xout iRnd
endop
opcode trirnd, i, iii
iMin, iMax, iMaxCount xin
;set a counter and accumulator
iCount = 0
iAccum = 0
;perform loop and accumulate
until iCount == iMaxCount do
iUniRnd random iMin, iMax
iAccum += iUniRnd
iCount += 1
enduntil
;get the mean and output
iRnd = iAccum / iMaxCount
xout iRnd
endop
;****ONE INSTRUMENT TO PERFORM ALL DISTRIBUTIONS****
;0 = uniform, 1 = linrnd_low, 2 = linrnd_high, 3 = trirnd
;the fractional part denotes the number of units, e.g.
;3.4 = triangular distribution with four sub-units
instr notes
;how many notes to be played
iHowMany = p4
;by which distribution with how many units
iWhich = giSequence[giSeqIndx]
iDistrib = int(iWhich)
iUnits = round(frac(iWhich) * 10)
;set min and max duration
iMinDur = .1
iMaxDur = 2
;set min and max pitch
iMinPch = 36
iMaxPch = 84
;trigger as many instances of instr play as needed
iThisNote = 0
iStart = 0
iPrint = 1
;for each note to be played
until iThisNote == iHowMany do
;calculate iMidiPch and iDur depending on type
if iDistrib == 0 then
printf_i "%s", iPrint, "... uniform distribution:\n"
printf_i "%s", iPrint, "EQUAL LIKELIHOOD OF ALL PITCHES AND DURATIONS\n"
iMidiPch random iMinPch, iMaxPch ;midi note
iDur random iMinDur, iMaxDur ;duration
elseif iDistrib == 1 then
printf_i "... linear low distribution with %d units:\n", iPrint, iUnits
printf_i "%s", iPrint, "LOWER NOTES AND LONGER DURATIONS PREFERRED\n"
iMidiPch linrnd_low iMinPch, iMaxPch, iUnits
iDur linrnd_high iMinDur, iMaxDur, iUnits
elseif iDistrib == 2 then
printf_i "... linear high distribution with %d units:\n", iPrint, iUnits
printf_i "%s", iPrint, "HIGHER NOTES AND SHORTER DURATIONS PREFERRED\n"
iMidiPch linrnd_high iMinPch, iMaxPch, iUnits
iDur linrnd_low iMinDur, iMaxDur, iUnits
else
printf_i "... triangular distribution with %d units:\n", iPrint, iUnits
printf_i "%s", iPrint, "MEDIUM NOTES AND DURATIONS PREFERRED\n"
iMidiPch trirnd iMinPch, iMaxPch, iUnits
iDur trirnd iMinDur, iMaxDur, iUnits
endif
;call subinstrument to play note
event_i "i", "play", iStart, iDur, int(iMidiPch)
;increase start tim and counter
iStart += iDur
iThisNote += 1
;avoid continuous printing
iPrint = 0
enduntil
;reset the duration of this instr to make all events happen
p3 = iStart + 2
;increase index for sequence
giSeqIndx += 1
;call instr again if sequence has not been ended
if giSeqIndx < lenarray(giSequence) then
event_i "i", "notes", p3, 1, iHowMany
;or exit
else
event_i "i", "exit", p3, 1
endif
endin
;****INSTRUMENTS TO PLAY THE SOUNDS AND EXIT CSOUND****
instr play
;increase duration in random range
iDur random p3, p3*1.5
p3 = iDur
;get midi note and convert to frequency
iMidiNote = p4
iFreq cpsmidinn iMidiNote
;generate note with karplus-strong algorithm
aPluck pluck .2, iFreq, iFreq, 0, 1
aPluck linen aPluck, 0, p3, p3
;filter
aFilter mode aPluck, iFreq, .1
;mix aPluck and aFilter according to MidiNote
;(high notes will be filtered more)
aMix ntrpol aPluck, aFilter, iMidiNote, 36, 84
;panning also according to MidiNote
;(low = left, high = right)
iPan = (iMidiNote-36) / 48
aL, aR pan2 aMix, iPan
outs aL, aR
endin
instr exit
exitnow
endin
</CsInstruments>
<CsScore>
i "notes" 0 1 23 ;set number of notes per instr here
e 99999 ;make possible to perform long (exit will be automatically)
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
With this method we can build probability distributions which are very similar to exponential or gaussian distributions.5 Their shape can easily be formed by the number of sub-units used.
Scalings
Random is a complex and sensible context. There are so many ways to let the horse go, run, or dance -- the conditions you set for this 'way of moving' are much more important than the fact that one single move is not predictable. What are the conditions of this randomness?
- Which Way. This is what has already been described: random with or without history, which probability distribution, etc.
- Which Range. This is a decision which comes from the composer/programmer. In the example above I have chosen pitches from Midi Note 36 to 84 (C2 to C6), and durations between 0.1 and 2 seconds. Imagine how it would have been sounded with pitches from 60 to 67, and durations from 0.9 to 1.1 seconds, or from 0.1 to 0.2 seconds. There is no range which is 'correct', everything depends on the musical idea.
- Which Development. Usually the boundaries will change in the run of a piece. The pitch range may move from low to high, or from narrow to wide; the durations may become shorter, etc.
- Which Scalings. Let us think about this more in detail.
In the example above we used two implicit scalings. The pitches have been scaled to the keys of a piano or keyboard. Why? We do not play piano here obviously ... -- What other possibilities might have been instead? One would be: no scaling at all. This is the easiest way to go -- whether it is really the best, or simple laziness, can only be decided by the composer or the listener.
Instead of using the equal tempered chromatic scale, or no scale at all, you can use any other ways of selecting or quantising pitches. Be it any which has been, or is still, used in any part of the world, or be it your own invention, by whatever fantasy or invention or system.
As regards the durations, the example above has shown no scaling at all. This was definitely laziness...
The next example is essentially the same as the previous one, but it uses a pitch scale which represents the overtone scale, starting at the second partial extending upwards to the 32nd partial. This scale is written into an array by a statement in instrument 0. The durations have fixed possible values which are written into an array (from the longest to the shortest) by hand. The values in both arrays are then called according to their position in the array.
EXAMPLE 01D06_scalings.csd
<CsoundSynthesizer>
<CsOptions>
-d -odac -m0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0
;****POSSIBLE DURATIONS AS ARRAY****
giDurs[] array 3/2, 1, 2/3, 1/2, 1/3, 1/4
giLenDurs lenarray giDurs
;****POSSIBLE PITCHES AS ARRAY****
;initialize array with 31 steps
giScale[] init 31
giLenScale lenarray giScale
;iterate to fill from 65 hz onwards
iStart = 65
iDenom = 3 ;start with 3/2
iCnt = 0
until iCnt = giLenScale do
giScale[iCnt] = iStart
iStart = iStart * iDenom / (iDenom-1)
iDenom += 1 ;next proportion is 4/3 etc
iCnt += 1
enduntil
;****SEQUENCE OF UNITS AS ARRAY****
giSequence[] array 0, 1.2, 1.4, 2.2, 2.4, 3.2, 3.6
giSeqIndx = 0 ;startindex
;****UDO DEFINITIONS****
opcode linrnd_low, i, iii
;linear random with precedence of lower values
iMin, iMax, iMaxCount xin
;set counter and initial (absurd) result
iCount = 0
iRnd = iMax
;loop and reset iRnd
until iCount == iMaxCount do
iUniRnd random iMin, iMax
iRnd = iUniRnd < iRnd ? iUniRnd : iRnd
iCount += 1
enduntil
xout iRnd
endop
opcode linrnd_high, i, iii
;linear random with precedence of higher values
iMin, iMax, iMaxCount xin
;set counter and initial (absurd) result
iCount = 0
iRnd = iMin
;loop and reset iRnd
until iCount == iMaxCount do
iUniRnd random iMin, iMax
iRnd = iUniRnd > iRnd ? iUniRnd : iRnd
iCount += 1
enduntil
xout iRnd
endop
opcode trirnd, i, iii
iMin, iMax, iMaxCount xin
;set a counter and accumulator
iCount = 0
iAccum = 0
;perform loop and accumulate
until iCount == iMaxCount do
iUniRnd random iMin, iMax
iAccum += iUniRnd
iCount += 1
enduntil
;get the mean and output
iRnd = iAccum / iMaxCount
xout iRnd
endop
;****ONE INSTRUMENT TO PERFORM ALL DISTRIBUTIONS****
;0 = uniform, 1 = linrnd_low, 2 = linrnd_high, 3 = trirnd
;the fractional part denotes the number of units, e.g.
;3.4 = triangular distribution with four sub-units
instr notes
;how many notes to be played
iHowMany = p4
;by which distribution with how many units
iWhich = giSequence[giSeqIndx]
iDistrib = int(iWhich)
iUnits = round(frac(iWhich) * 10)
;trigger as many instances of instr play as needed
iThisNote = 0
iStart = 0
iPrint = 1
;for each note to be played
until iThisNote == iHowMany do
;calculate iMidiPch and iDur depending on type
if iDistrib == 0 then
printf_i "%s", iPrint, "... uniform distribution:\n"
printf_i "%s", iPrint, "EQUAL LIKELINESS OF ALL PITCHES AND DURATIONS\n"
iScaleIndx random 0, giLenScale-.0001 ;midi note
iDurIndx random 0, giLenDurs-.0001 ;duration
elseif iDistrib == 1 then
printf_i "... linear low distribution with %d units:\n", iPrint, iUnits
printf_i "%s", iPrint, "LOWER NOTES AND LONGER DURATIONS PREFERRED\n"
iScaleIndx linrnd_low 0, giLenScale-.0001, iUnits
iDurIndx linrnd_low 0, giLenDurs-.0001, iUnits
elseif iDistrib == 2 then
printf_i "... linear high distribution with %d units:\n", iPrint, iUnits
printf_i "%s", iPrint, "HIGHER NOTES AND SHORTER DURATIONS PREFERRED\n"
iScaleIndx linrnd_high 0, giLenScale-.0001, iUnits
iDurIndx linrnd_high 0, giLenDurs-.0001, iUnits
else
printf_i "... triangular distribution with %d units:\n", iPrint, iUnits
printf_i "%s", iPrint, "MEDIUM NOTES AND DURATIONS PREFERRED\n"
iScaleIndx trirnd 0, giLenScale-.0001, iUnits
iDurIndx trirnd 0, giLenDurs-.0001, iUnits
endif
;call subinstrument to play note
iDur = giDurs[int(iDurIndx)]
iPch = giScale[int(iScaleIndx)]
event_i "i", "play", iStart, iDur, iPch
;increase start time and counter
iStart += iDur
iThisNote += 1
;avoid continuous printing
iPrint = 0
enduntil
;reset the duration of this instr to make all events happen
p3 = iStart + 2
;increase index for sequence
giSeqIndx += 1
;call instr again if sequence has not been ended
if giSeqIndx < lenarray(giSequence) then
event_i "i", "notes", p3, 1, iHowMany
;or exit
else
event_i "i", "exit", p3, 1
endif
endin
;****INSTRUMENTS TO PLAY THE SOUNDS AND EXIT CSOUND****
instr play
;increase duration in random range
iDur random p3*2, p3*5
p3 = iDur
;get frequency
iFreq = p4
;generate note with karplus-strong algorithm
aPluck pluck .2, iFreq, iFreq, 0, 1
aPluck linen aPluck, 0, p3, p3
;filter
aFilter mode aPluck, iFreq, .1
;mix aPluck and aFilter according to freq
;(high notes will be filtered more)
aMix ntrpol aPluck, aFilter, iFreq, 65, 65*16
;panning also according to freq
;(low = left, high = right)
iPan = (iFreq-65) / (65*16)
aL, aR pan2 aMix, iPan
outs aL, aR
endin
instr exit
exitnow
endin
</CsInstruments>
<CsScore>
i "notes" 0 1 23 ;set number of notes per instr here
e 99999 ;make possible to perform long (exit will be automatically)
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Random With History
There are many ways a current value in a random number progression can influence the next. Two of them are used frequently. A Markov chain is based on a number of possible states, and defines a different probability for each of these states. A random walk looks at the last state as a position in a range or field, and allows only certain deviations from this position.
Markov Chains
A typical case for a Markov chain in music is a sequence of certain pitches or notes. For each note, the probability of the following note is written in a table like this:

This means: the probability that element a is repeated, is 0.2; the probability that b follows a is 0.5; the probability that c follows a is 0.3. The sum of all probabilities must, by convention, add up to 1. The following example shows the basic algorithm which evaluates the first line of the Markov table above, in the case, the previous element has been 'a'.
EXAMPLE 01D07_markov_basics.csd
<CsoundSynthesizer>
<CsOptions>
-ndm0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
0dbfs = 1
nchnls = 1
seed 0
instr 1
iLine[] array .2, .5, .3
iVal random 0, 1
iAccum = iLine[0]
iIndex = 0
until iAccum >= iVal do
iIndex += 1
iAccum += iLine[iIndex]
enduntil
printf_i "Random number = %.3f, next element = %c!\n", 1, iVal, iIndex+97
endin
</CsInstruments>
<CsScore>
r 10
i 1 0 0
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
The probabilities are 0.2 0.5 0.3. First a uniformly distributed random number between 0 and 1 is generated. An acculumator is set to the first element of the line (here 0.2). It is interrogated as to whether it is larger than the random number. If so then the index is returned, if not, the second element is added (0.2+0.5=0.7), and the process is repeated, until the accumulator is greater or equal the random value. The output of the example should show something like this:
Random number = 0.850, next element = c!
Random number = 0.010, next element = a!
Random number = 0.805, next element = c!
Random number = 0.696, next element = b!
Random number = 0.626, next element = b!
Random number = 0.476, next element = b!
Random number = 0.420, next element = b!
Random number = 0.627, next element = b!
Random number = 0.065, next element = a!
Random number = 0.782, next element = c!
The next example puts this algorithm in an User Defined Opcode. Its input is a Markov table as a two-dimensional array, and the previous line as index (starting with 0). Its output is the next element, also as index. -- There are two Markov chains in this example: seven pitches, and three durations. Both are defined in two-dimensional arrays: giProbNotes and giProbDurs. Both Markov chains are running independently from each other.
EXAMPLE 01D08_markov_music.csd
<CsoundSynthesizer>
<CsOptions>
-dnm128 -odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
0dbfs = 1
nchnls = 2
seed 0
;****USER DEFINED OPCODES FOR MARKOV CHAINS****
opcode Markov, i, i[][]i
iMarkovTable[][], iPrevEl xin
iRandom random 0, 1
iNextEl = 0
iAccum = iMarkovTable[iPrevEl][iNextEl]
until iAccum >= iRandom do
iNextEl += 1
iAccum += iMarkovTable[iPrevEl][iNextEl]
enduntil
xout iNextEl
endop
opcode Markovk, k, k[][]k
kMarkovTable[][], kPrevEl xin
kRandom random 0, 1
kNextEl = 0
kAccum = kMarkovTable[kPrevEl][kNextEl]
until kAccum >= kRandom do
kNextEl += 1
kAccum += kMarkovTable[kPrevEl][kNextEl]
enduntil
xout kNextEl
endop
;****DEFINITIONS FOR NOTES****
;notes as proportions and a base frequency
giNotes[] array 1, 9/8, 6/5, 5/4, 4/3, 3/2, 5/3
giBasFreq = 330
;probability of notes as markov matrix:
;first -> only to third and fourth
;second -> anywhere without self
;third -> strong probability for repetitions
;fourth -> idem
;fifth -> anywhere without third and fourth
;sixth -> mostly to seventh
;seventh -> mostly to sixth
giProbNotes[][] init 7, 7
giProbNotes array 0.0, 0.0, 0.5, 0.5, 0.0, 0.0, 0.0,
0.2, 0.0, 0.2, 0.2, 0.2, 0.1, 0.1,
0.1, 0.1, 0.5, 0.1, 0.1, 0.1, 0.0,
0.0, 0.1, 0.1, 0.5, 0.1, 0.1, 0.1,
0.2, 0.2, 0.0, 0.0, 0.2, 0.2, 0.2,
0.1, 0.1, 0.0, 0.0, 0.1, 0.1, 0.6,
0.1, 0.1, 0.0, 0.0, 0.1, 0.6, 0.1
;****DEFINITIONS FOR DURATIONS****
;possible durations
gkDurs[] array 1, 1/2, 1/3
;probability of durations as markov matrix:
;first -> anything
;second -> mostly self
;third -> mostly second
gkProbDurs[][] init 3, 3
gkProbDurs array 1/3, 1/3, 1/3,
0.2, 0.6, 0.3,
0.1, 0.5, 0.4
;****SET FIRST NOTE AND DURATION FOR MARKOV PROCESS****
giPrevNote init 1
gkPrevDur init 1
;****INSTRUMENT FOR DURATIONS****
instr trigger_note
kTrig metro 1/gkDurs[gkPrevDur]
if kTrig == 1 then
event "i", "select_note", 0, 1
gkPrevDur Markovk gkProbDurs, gkPrevDur
endif
endin
;****INSTRUMENT FOR PITCHES****
instr select_note
;choose next note according to markov matrix and previous note
;and write it to the global variable for (next) previous note
giPrevNote Markov giProbNotes, giPrevNote
;call instr to play this note
event_i "i", "play_note", 0, 2, giPrevNote
;turn off this instrument
turnoff
endin
;****INSTRUMENT TO PERFORM ONE NOTE****
instr play_note
;get note as index in ginotes array and calculate frequency
iNote = p4
iFreq = giBasFreq * giNotes[iNote]
;random choice for mode filter quality and panning
iQ random 10, 200
iPan random 0.1, .9
;generate tone and put out
aImp mpulse 1, p3
aOut mode aImp, iFreq, iQ
aL, aR pan2 aOut, iPan
outs aL, aR
endin
</CsInstruments>
<CsScore>
i "trigger_note" 0 100
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Random Walk
In the context of movement between random values, 'walk' can be thought of as the opposite of 'jump'. If you jump within the boundaries A and B, you can end up anywhere between these boundaries, but if you walk between A and B you will be limited by the extent of your step - each step applies a deviation to the previous one. If the deviation range is slightly more positive (say from -0.1 to +0.2), the general trajectory of your walk will be in the positive direction (but individual steps will not necessarily be in the positive direction). If the deviation range is weighted negative (say from -0.2 to 0.1), then the walk will express a generally negative trajectory.
One way of implementing a random walk will be to take the current state, derive a random deviation, and derive the next state by adding this deviation to the current state. The next example shows two ways of doing this.
The pitch random walk starts at pitch 8 in octave notation. The general pitch deviation gkPitchDev is set to 0.2, so that the next pitch could be between 7.8 and 8.2. But there is also a pitch direction gkPitchDir which is set to 0.1 as initial value. This means that the upper limit of the next random pitch is 8.3 instead of 8.2, so that the pitch will move upwards in a greater number of steps. When the upper limit giHighestPitch has been crossed, the gkPitchDir variable changes from +0.1 to -0.1, so after a number of steps, the pitch will have become lower. Whenever such a direction change happens, the console reports this with a message printed to the terminal.
The density of the notes is defined as notes per second, and is applied as frequency to the metro opcode in instrument 'walk'. The lowest possible density giLowestDens is set to 1, the highest to 8 notes per second, and the first density giStartDens is set to 3. The possible random deviation for the next density is defined in a range from zero to one: zero means no deviation at all, one means that the next density can alter the current density in a range from half the current value to twice the current value. For instance, if the current density is 4, for gkDensDev=1 you would get a density between 2 and 8. The direction of the densities gkDensDir in this random walk follows the same range 0..1. Assumed you have no deviation of densities at all (gkDensDev=0), gkDensDir=0 will produce ticks in always the same speed, whilst gkDensDir=1 will produce a very rapid increase in speed. Similar to the pitch walk, the direction parameter changes from plus to minus if the upper border has crossed, and vice versa.
EXAMPLE 01D09_random_walk.csd
<CsoundSynthesizer>
<CsOptions>
-dnm128 -odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
0dbfs = 1
nchnls = 2
seed 1 ;change to zero for always changing results
;****SETTINGS FOR PITCHES****
;define the pitch street in octave notation
giLowestPitch = 7
giHighestPitch = 9
;set pitch startpoint, deviation range and the first direction
giStartPitch = 8
gkPitchDev init 0.2 ;random range for next pitch
gkPitchDir init 0.1 ;positive = upwards
;****SETTINGS FOR DENSITY****
;define the maximum and minimum density (notes per second)
giLowestDens = 1
giHighestDens = 8
;set first density
giStartDens = 3
;set possible deviation in range 0..1
;0 = no deviation at all
;1 = possible deviation is between half and twice the current density
gkDensDev init 0.5
;set direction in the same range 0..1
;(positive = more dense, shorter notes)
gkDensDir init 0.1
;****INSTRUMENT FOR RANDOM WALK****
instr walk
;set initial values
kPitch init giStartPitch
kDens init giStartDens
;trigger impulses according to density
kTrig metro kDens
;if the metro ticks
if kTrig == 1 then
;1) play current note
event "i", "play", 0, 1.5/kDens, kPitch
;2) calculate next pitch
;define boundaries according to direction
kLowPchBound = gkPitchDir < 0 ? -gkPitchDev+gkPitchDir : -gkPitchDev
kHighPchBound = gkPitchDir > 0 ? gkPitchDev+gkPitchDir : gkPitchDev
;get random value in these boundaries
kPchRnd random kLowPchBound, kHighPchBound
;add to current pitch
kPitch += kPchRnd
;change direction if maxima are crossed, and report
if kPitch > giHighestPitch && gkPitchDir > 0 then
gkPitchDir = -gkPitchDir
printks " Pitch touched maximum - now moving down.\n", 0
elseif kPitch < giLowestPitch && gkPitchDir < 0 then
gkPitchDir = -gkPitchDir
printks "Pitch touched minimum - now moving up.\n", 0
endif
;3) calculate next density (= metro frequency)
;define boundaries according to direction
kLowDensBound = gkDensDir < 0 ? -gkDensDev+gkDensDir : -gkDensDev
kHighDensBound = gkDensDir > 0 ? gkDensDev+gkDensDir : gkDensDev
;get random value in these boundaries
kDensRnd random kLowDensBound, kHighDensBound
;get multiplier (so that kDensRnd=1 yields to 2, and kDens=-1 to 1/2)
kDensMult = 2 ^ kDensRnd
;multiply with current duration
kDens *= kDensMult
;avoid too high values and too low values
kDens = kDens > giHighestDens*1.5 ? giHighestDens*1.5 : kDens
kDens = kDens < giLowestDens/1.5 ? giLowestDens/1.5 : kDens
;change direction if maxima are crossed
if (kDens > giHighestDens && gkDensDir > 0) || (kDens < giLowestDens && gkDensDir < 0) then
gkDensDir = -gkDensDir
if kDens > giHighestDens then
printks " Density touched upper border - now becoming less dense.\n", 0
else
printks " Density touched lower border - now becoming more dense.\n", 0
endif
endif
endif
endin
;****INSTRUMENT TO PLAY ONE NOTE****
instr play
;get note as octave and calculate frequency and panning
iOct = p4
iFreq = cpsoct(iOct)
iPan ntrpol 0, 1, iOct, giLowestPitch, giHighestPitch
;calculate mode filter quality according to duration
iQ ntrpol 10, 400, p3, .15, 1.5
;generate tone and throw out
aImp mpulse 1, p3
aMode mode aImp, iFreq, iQ
aOut linen aMode, 0, p3, p3/4
aL, aR pan2 aOut, iPan
outs aL, aR
endin
</CsInstruments>
<CsScore>
i "walk" 0 999
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
II. SOME MATHS PERSPECTIVES ON RANDOM
Random Processes
The relative frequency of occurrence of a random variable can be described by a probability function (for discrete random variables) or by density functions (for continuous random variables).
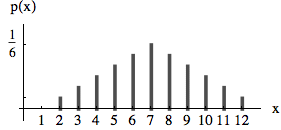
When two dice are thrown simultaneously, the sum x of their numbers can be 2, 3, ...12. The following figure shows the probability function p(x) of these possible outcomes. p(x) is always less than or equal to 1. The sum of the probabilities of all possible outcomes is 1.
For continuous random variables the probability of getting a specific value x is 0. But the probability of getting a value within a certain interval can be indicated by an area that corresponds to this probability. The function f(x) over these areas is called the density function. With the following density the chance of getting a number smaller than 0 is 0, to get a number between 0 and 0.5 is 0.5, to get a number between 0.5 and 1 is 0.5 etc. Density functions f(x) can reach values greater than 1 but the area under the function is 1.
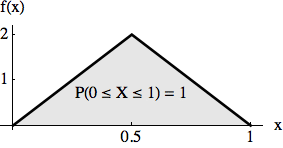
Generating Random Numbers With a Given Probability or Density
Csound provides opcodes for some specific densities but no means to produce random number with user defined probability or density functions. The opcodes rand_density and rand_probability (see below) generate random numbers with probabilities or densities given by tables. They are realized by using the so-called rejection sampling method.
Rejection Sampling:
The principle of rejection sampling is to first generate uniformly distributed random numbers in the range required and to then accept these values corresponding to a given density function (or otherwise reject them). Let us demonstrate this method using the density function shown in the next figure. (Since the rejection sampling method uses only the "shape" of the function, the area under the function need not be 1). We first generate uniformly distributed random numbers rnd1 over the interval [0, 1]. Of these we accept a proportion corresponding to f(rnd1). For example, the value 0.32 will only be accepted in the proportion of f(0.32) = 0.82. We do this by generating a new random number rand2 between 0 and 1 and accept rnd1 only if rand2 < f(rnd1); otherwise we reject it. (see Signals, Systems and Sound Synthesis6 chapter 10.1.4.4)

EXAMPLE 01D10_Rejection_Sampling.csd
<CsoundSynthesizer> <CsOptions> -odac </CsOptions> <CsInstruments> ;example by martin neukom sr = 44100 ksmps = 10 nchnls = 1 0dbfs = 1 ; random number generator to a given density function ; kout random number; k_minimum,k_maximum,i_fn for a density function opcode rand_density, k, kki kmin,kmax,ifn xin loop: krnd1 random 0,1 krnd2 random 0,1 k2 table krnd1,ifn,1 if krnd2 > k2 kgoto loop xout kmin+krnd1*(kmax-kmin) endop ; random number generator to a given probability function ; kout random number ; in: i_nr number of possible values ; i_fn1 function for random values ; i_fn2 probability functionExponential: Generate a uniformly distributed number between 0 and 1 and take its natural logarithm. opcode rand_probability, k, iii inr,ifn1,ifn2 xin loop: krnd1 random 0,inr krnd2 random 0,1 k2 table int(krnd1),ifn2,0 if krnd2 > k2 kgoto loop kout table krnd1,ifn1,0 xout kout endop instr 1 krnd rand_density 400,800,2 aout poscil .1,krnd,1 out aout endin instr 2 krnd rand_probability p4,p5,p6 aout poscil .1,krnd,1 out aout endin </CsInstruments> <CsScore> ;sine f1 0 32768 10 1 ;density function f2 0 1024 6 1 112 0 800 0 112 1 ;random values and their relative probability (two dice) f3 0 16 -2 2 3 4 5 6 7 8 9 10 11 12 f4 0 16 2 1 2 3 4 5 6 5 4 3 2 1 ;random values and their relative probability f5 0 8 -2 400 500 600 800 f6 0 8 2 .3 .8 .3 .1 i1 0 10 i2 0 10 4 5 6 </CsScore> </CsoundSynthesizer>
Random Walk
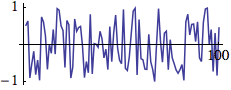
In a series of random numbers the single numbers are independent upon each other. Parameter (left figure) or paths in the room (two-dimensional trajectory in the right figure) created by random numbers wildly jump around.
Example 1
Table[RandomReal[{-1, 1}], {100}];

We get a smoother path, a so-called random walk, by adding at every time step a random number r to the actual position x (x += r).
Example 2
x = 0; walk = Table[x += RandomReal[{-.2, .2}], {300}];
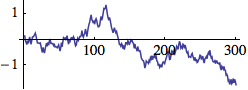

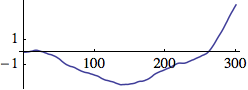
The path becomes even smoother by adding a random number r to the actual velocity v.
v += r
x += v
The path can be bounded to an area (figure to the right) by inverting the velocity if the path exceeds the limits (min, max):
vif(x < min || x > max) v *= -1
The movement can be damped by decreasing the velocity at every time step by a small factor d
v *= (1-d)
Example 3
x = 0; v = 0; walk = Table[x += v += RandomReal[{-.01, .01}], {300}];

The path becomes again smoother by adding a random number r to the actual acelleration a, the change of the aceleration, etc.
a += r
v += a
x += v
Example 4
x = 0; v = 0; a = 0;
Table[x += v += a += RandomReal[{-.0001, .0001}], {300}];
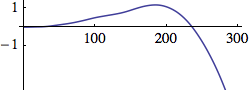

(see Martin Neukom, Signals, Systems and Sound Synthesis chapter 10.2.3.2)
EXAMPLE 01D11_Random_Walk2.csd
<CsoundSynthesizer> <CsOptions> -odac </CsOptions> <CsInstruments> ;example by martin neukom sr = 44100 ksmps = 128 nchnls = 1 0dbfs = 1 ; random frequency instr 1 kx random -p6, p6 kfreq = p5*2^kx aout oscil p4, kfreq, 1 out aout endin ; random change of frequency instr 2 kx init .5 kfreq = p5*2^kx kv random -p6, p6 kv = kv*(1 - p7) kx = kx + kv aout oscil p4, kfreq, 1 out aout endin ; random change of change of frequency instr 3 kv init 0 kx init .5 kfreq = p5*2^kx ka random -p7, p7 kv = kv + ka kv = kv*(1 - p8) kx = kx + kv kv = (kx < -p6 || kx > p6?-kv : kv) aout oscili p4, kfreq, 1 out aout endin </CsInstruments> <CsScore> f1 0 32768 10 1 ; i1 p4 p5 p6 ; i2 p4 p5 p6 p7 ; amp c_fr rand damp ; i2 0 20 .1 600 0.01 0.001 ; amp c_fr d_fr rand damp ; amp c_fr rand ; i1 0 20 .1 600 0.5 ; i3 p4 p5 p6 p7 p8 i3 0 20 .1 600 1 0.001 0.001 </CsScore> </CsoundSynthesizer>
III. MISCELLANEOUS EXAMPLES
Csound has a range of opcodes and GEN routine for the creation of various random functions and distributions. Perhaps the simplest of these is random which simply generates a random value within user defined minimum and maximum limit and at i-time, k-rate or a-rate accroding to the variable type of its output:
ires random imin, imax kres random kmin, kmax ares random kmin, kmax
Values are generated according to a uniform random distribution, meaning that any value within the limits has equal chance of occurence. Non-uniform distributions in which certain values have greater chance of occurence over others are often more useful and musical. For these purposes, Csound includes the betarand, bexprand, cauchy, exprand, gauss, linrand, pcauchy, poisson, trirand, unirand and weibull random number generator opcodes. The distributions generated by several of these opcodes are illustrated below.

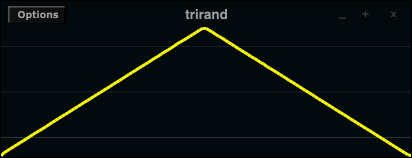

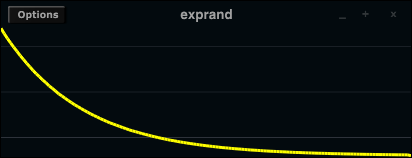
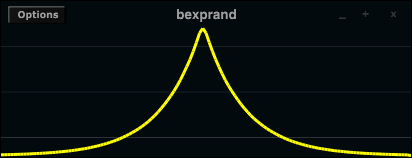
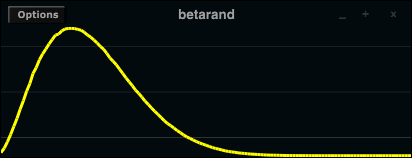
In addition to these so called 'x-class noise generators' Csound provides random function generators, providing values that change over time a various ways.
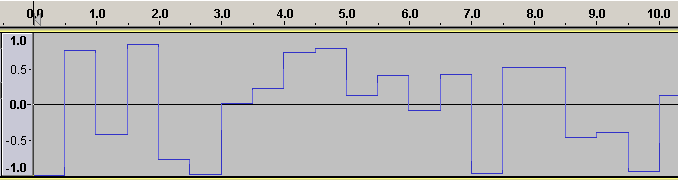
randomh generates new random numbers at a user defined rate. The previous value is held until a new value is generated, and then the output immediately assumes that value.
The instruction:
kmin = -1 kmax = 1 kfreq = 2 kout randomh kmin,kmax,kfreq
will produce and output something like:
randomi is an interpolating version of randomh. Rather than jump to new values when they are generated, randomi interpolates linearly to the new value, reaching it just as a new random value is generated. Replacing randomh with randomi in the above code snippet would result in the following output:
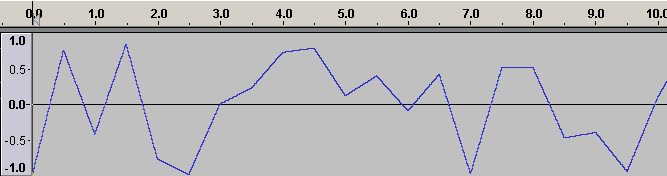
In practice randomi's angular changes in direction as new random values are generated might be audible depending on the how it is used. rsplsine (or the simpler jsplsine) allows us to specify not just a single frequency but a minimum and a maximum frequency, and the resulting function is a smooth spline between the minimum and maximum values and these minimum and maximum frequencies. The following input:
kmin = -0.95 kmax = 0.95 kminfrq = 1 kmaxfrq = 4 asig rspline kmin, kmax, kminfrq, kmaxfrq
would generate an output something like:
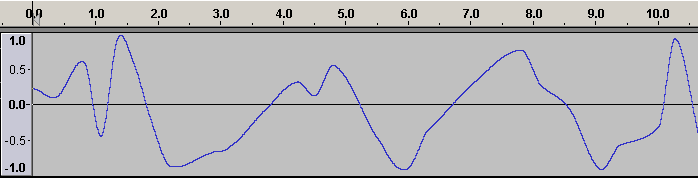
We need to be careful with what we do with rspline's output as it can exceed the limits set by kmin and kmax. Minimum and maximum values can be set conservatively or the limit opcode could be used to prevent out of range values that could cause problems.
The following example uses rspline to 'humanise' a simple synthesiser. A short melody is played, first without any humanising and then with humanising. rspline random variation is added to the amplitude and pitch of each note in addition to an i-time random offset.
EXAMPLE 01D12_humanising.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0
giWave ftgen 0, 0, 2^10, 10, 1,0,1/4,0,1/16,0,1/64,0,1/256,0,1/1024
instr 1 ; an instrument with no 'humanising'
inote = p4
aEnv linen 0.1,0.01,p3,0.01
aSig poscil aEnv,cpsmidinn(inote),giWave
outs aSig,aSig
endin
instr 2 ; an instrument with 'humanising'
inote = p4
; generate some i-time 'static' random paramters
iRndAmp random -3,3 ; amp. will be offset by a random number of decibels
iRndNte random -5,5 ; note will be offset by a random number of cents
; generate some k-rate random functions
kAmpWob rspline -1,1,1,10 ; amplitude 'wobble' (in decibels)
kNteWob rspline -5,5,0.3,10 ; note 'wobble' (in cents)
; calculate final note function (in CPS)
kcps = cpsmidinn(inote+(iRndNte*0.01)+(kNteWob*0.01))
; amplitude envelope (randomisation of attack time)
aEnv linen 0.1*ampdb(iRndAmp+kAmpWob),0.01+rnd(0.03),p3,0.01
aSig poscil aEnv,kcps,giWave
outs aSig,aSig
endin
</CsInstruments>
<CsScore>
t 0 80
#define SCORE(i) #
i $i 0 1 60
i . + 2.5 69
i . + 0.5 67
i . + 0.5 65
i . + 0.5 64
i . + 3 62
i . + 1 62
i . + 2.5 70
i . + 0.5 69
i . + 0.5 67
i . + 0.5 65
i . + 3 64 #
$SCORE(1) ; play melody without humanising
b 17
$SCORE(2) ; play melody with humanising
e
</CsScore>
</CsoundSynthesizer>
;example by Iain McCurdy
The final example implements a simple algorithmic note generator. It makes use of GEN17 to generate histograms which define the probabilities of certain notes and certain rhythmic gaps occuring.
EXAMPLE 01D13_simple_algorithmic_note_generator.csd
<CsoundSynthesizer>
<CsOptions>
-odac -dm0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giNotes ftgen 0,0,-100,-17,0,48, 15,53, 30,55, 40,60, 50,63, 60,65, 79,67, 85,70, 90,72, 96,75
giDurs ftgen 0,0,-100,-17,0,2, 30,0.5, 75,1, 90,1.5
instr 1
kDur init 0.5 ; initial rhythmic duration
kTrig metro 2/kDur ; metronome freq. 2 times inverse of duration
kNdx trandom kTrig,0,1 ; create a random index upon each metro 'click'
kDur table kNdx,giDurs,1 ; read a note duration value
schedkwhen kTrig,0,0,2,0,1 ; trigger a note!
endin
instr 2
iNote table rnd(1),giNotes,1 ; read a random value from the function table
aEnv linsegr 0, 0.005, 1, p3-0.105, 1, 0.1, 0 ; amplitude envelope
iPlk random 0.1, 0.3 ; point at which to pluck the string
iDtn random -0.05, 0.05 ; random detune
aSig wgpluck2 0.98, 0.2, cpsmidinn(iNote+iDtn), iPlk, 0.06
out aSig * aEnv
endin
</CsInstruments>
<CsScore>
i 1 0 300 ; start 3 long notes close after one another
i 1 0.01 300
i 1 0.02 300
e
</CsScore>
</CsoundSynthesizer>
;example by Iain McCurdy
- http://www.etymonline.com/index.php?term=random^
- Because the sample rate is 44100 samples per second. So a repetition after 65536 samples will lead to a repetition after 65536/44100 = 1.486 seconds.^
- Charles Dodge and Thomas A. Jerse, Computer Music, New York 1985, Chapter 8.1, in particular page 269-278.^
- Most of them have been written by Paris Smaragdis in 1995: betarnd, bexprnd, cauchy, exprnd, gauss, linrand, pcauchy, poisson, trirand, unirand and weibull.^
- According to Dodge/Jerse, the usual algorithms for exponential and gaussian are:
Exponential: Generate a uniformly distributed number between 0 and 1 and take its natural logarithm.
Gauss: Take the mean of uniformly distributed numbers and scale them by the standard deviation. ^ - Neukom, Martin. Signals, systems and sound synthesis. Bern: Peter Lang, 2013. Print. ^