CSOUND
Csound: AdditiveSynthesis
ADDITIVE SYNTHESIS
Jean Baptiste Joseph Fourier demonstrated in around 1800 that any continuous function can be described perfectly as a sum of sine waves. This means that you can create any sound, no matter how complex, if you know how many sine waves, and at what frequencies, to add together.
This concept really excited the early pioneers of electronic music, who imagined that sine waves would give them the power to create any sound imaginable and previously unimagined sounds. Unfortunately, they soon realised that while adding sine waves is easy, interesting sounds require a large number of sine waves that are varying constantly in frequency and amplitude and this turns out to be a hugely impractical task.
Nonetheless, additive synthesis can provide unusual and interesting sounds and the power of modern computers and their ability to manage data in a programming language offers new dimensions of working with this old technique. As with most things in Csound there are several ways to go about implementing additive synthesis. We shall endeavour to introduce some of them and to allude to how they relate to different programming paradigms.
What are the Main Parameters of Additive Synthesis?
Before examining various methods of implementing additive synthesis in Csound, we shall first consider what parameters might be required. As additive synthesis involves the addition of multiple sine generators, the parameters we use will operate on one of two different levels:
- For each sine, there will be a frequency and an amplitude with an envelope.
- The frequency will usually be a constant value, but it can be varied and in fact natural sounds typically exhibit slight modulations of partial frequencies.
- The amplitude must have at least a simple envelope such as the well-known ADSR but more complex methods of continuously altering the amplitude will result in a livelier sound.
- For the sound as an entirety, the relevant parameters are:
- The total number of sinusoids. A sound which consists of just three sinusoids will most likely sound poorer than one which employs 100.
- The frequency ratios of the sine generators. For a classic harmonic spectrum, the multipliers of the sinusoids are 1, 2, 3, ... (If your first sine is 100 Hz, the others will be 200, 300, 400, ... Hz.) An inharmonic or noisy spectrum will probably have no simple integer ratios. These frequency ratios are chiefly responsible for our perception of timbre.
- The base frequency is the frequency of the first partial. If the partials are exhibiting a harmonic ratio, this frequency (in the example given 100 Hz) is also the overall perceived pitch.
- The amplitude ratios of the sinusoids. This is also very important in determining the resulting timbre of a sound. If the higher partials are relatively strong, the sound will be perceived as being more 'brilliant'; if the higher partials are soft, then the sound will be perceived as being dark and soft.
- The duration ratios of the sinusoids. In simple additive synthesis, all single sines have the same duration, but it will be more interesting if they differ - this will usually relate to the durations of the envelopes: if the envelopes of different partials vary, some partials will die away faster than others.
It is not always the aim of additive synthesis to imitate natural sounds, but the task of first analysing and then attempting to imitate a sound can prove to be very useful when studying additive synthesis. This is what a guitar note looks like when spectrally analysed:
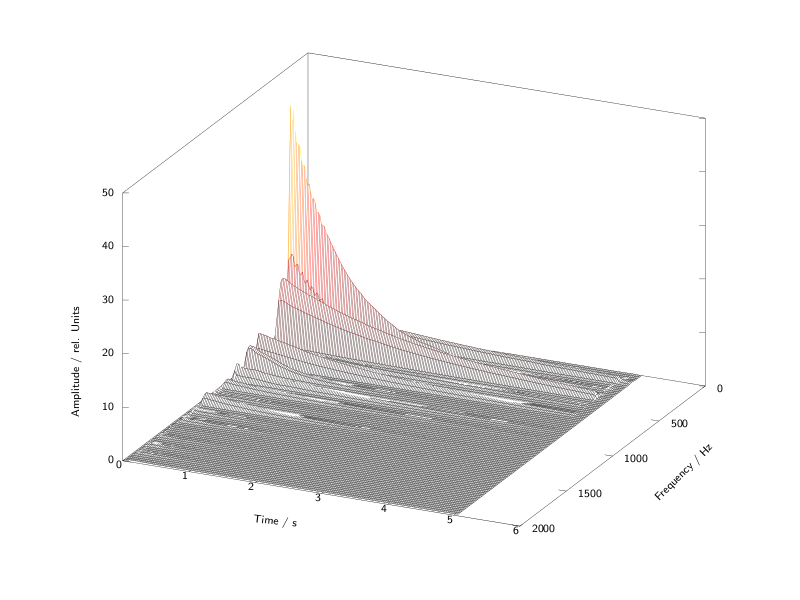
Spectral analysis of a guitar tone in time (courtesy of W. Fohl, Hamburg)
Each partial possesses its own frequency movement and duration. We may or may not be able to achieve this successfully using additive synthesis. Let us begin with some simple sounds and consider how to go about programming this in Csound. Later we will look at some more complex sounds and the more advanced techniques required to synthesize them.
Simple Additions of Sinusoids Inside an Instrument
If additive synthesis amounts to simply adding together sine generators, it is therefore straightforward to implement this by creating multiple oscillators in a single instrument and adding their outputs together. In the following example, instrument 1 demonstrates the creation of a harmonic spectrum, and instrument 2 an inharmonic one. Both instruments share the same amplitude multipliers: 1, 1/2, 1/3, 1/4, ... and receive the base frequency in Csound's pitch notation (octave.semitone) and the main amplitude in dB.
EXAMPLE 04A01_AddSynth_simple.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;example by Andrés Cabrera
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
instr 1 ;harmonic additive synthesis
;receive general pitch and volume from the score
ibasefrq = cpspch(p4) ;convert pitch values to frequency
ibaseamp = ampdbfs(p5) ;convert dB to amplitude
;create 8 harmonic partials
aOsc1 poscil ibaseamp, ibasefrq, giSine
aOsc2 poscil ibaseamp/2, ibasefrq*2, giSine
aOsc3 poscil ibaseamp/3, ibasefrq*3, giSine
aOsc4 poscil ibaseamp/4, ibasefrq*4, giSine
aOsc5 poscil ibaseamp/5, ibasefrq*5, giSine
aOsc6 poscil ibaseamp/6, ibasefrq*6, giSine
aOsc7 poscil ibaseamp/7, ibasefrq*7, giSine
aOsc8 poscil ibaseamp/8, ibasefrq*8, giSine
;apply simple envelope
kenv linen 1, p3/4, p3, p3/4
;add partials and write to output
aOut = aOsc1 + aOsc2 + aOsc3 + aOsc4 + aOsc5 + aOsc6 + aOsc7 + aOsc8
outs aOut*kenv, aOut*kenv
endin
instr 2 ;inharmonic additive synthesis
ibasefrq = cpspch(p4)
ibaseamp = ampdbfs(p5)
;create 8 inharmonic partials
aOsc1 poscil ibaseamp, ibasefrq, giSine
aOsc2 poscil ibaseamp/2, ibasefrq*1.02, giSine
aOsc3 poscil ibaseamp/3, ibasefrq*1.1, giSine
aOsc4 poscil ibaseamp/4, ibasefrq*1.23, giSine
aOsc5 poscil ibaseamp/5, ibasefrq*1.26, giSine
aOsc6 poscil ibaseamp/6, ibasefrq*1.31, giSine
aOsc7 poscil ibaseamp/7, ibasefrq*1.39, giSine
aOsc8 poscil ibaseamp/8, ibasefrq*1.41, giSine
kenv linen 1, p3/4, p3, p3/4
aOut = aOsc1 + aOsc2 + aOsc3 + aOsc4 + aOsc5 + aOsc6 + aOsc7 + aOsc8
outs aOut*kenv, aOut*kenv
endin
</CsInstruments>
<CsScore>
; pch amp
i 1 0 5 8.00 -13
i 1 3 5 9.00 -17
i 1 5 8 9.02 -15
i 1 6 9 7.01 -15
i 1 7 10 6.00 -13
s
i 2 0 5 8.00 -13
i 2 3 5 9.00 -17
i 2 5 8 9.02 -15
i 2 6 9 7.01 -15
i 2 7 10 6.00 -13
</CsScore>
</CsoundSynthesizer>
Simple Additions of Sinusoids via the Score
A typical paradigm in programming: if you are repeating lines of code with just minor variations, consider abstracting it in some way. In the Csound language this could mean moving parameter control to the score. In our case, the lines
aOsc1 poscil ibaseamp, ibasefrq, giSine aOsc2 poscil ibaseamp/2, ibasefrq*2, giSine aOsc3 poscil ibaseamp/3, ibasefrq*3, giSine aOsc4 poscil ibaseamp/4, ibasefrq*4, giSine aOsc5 poscil ibaseamp/5, ibasefrq*5, giSine aOsc6 poscil ibaseamp/6, ibasefrq*6, giSine aOsc7 poscil ibaseamp/7, ibasefrq*7, giSine aOsc8 poscil ibaseamp/8, ibasefrq*8, giSine
could be abstracted to the form
aOsc poscil ibaseamp*iampfactor, ibasefrq*ifreqfactor, giSine
with the parameters iampfactor (the relative amplitude of a partial) and ifreqfactor (the frequency multiplier) being transferred to the score as p-fields.
The next version of the previous instrument, simplifies the instrument code and defines the variable values as score parameters:
EXAMPLE 04A02_AddSynth_score.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;example by Andrés Cabrera and Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
instr 1
iBaseFreq = cpspch(p4)
iFreqMult = p5 ;frequency multiplier
iBaseAmp = ampdbfs(p6)
iAmpMult = p7 ;amplitude multiplier
iFreq = iBaseFreq * iFreqMult
iAmp = iBaseAmp * iAmpMult
kEnv linen iAmp, p3/4, p3, p3/4
aOsc poscil kEnv, iFreq, giSine
outs aOsc, aOsc
endin
</CsInstruments>
<CsScore>
; freq freqmult amp ampmult
i 1 0 7 8.09 1 -10 1
i . . 6 . 2 . [1/2]
i . . 5 . 3 . [1/3]
i . . 4 . 4 . [1/4]
i . . 3 . 5 . [1/5]
i . . 3 . 6 . [1/6]
i . . 3 . 7 . [1/7]
s
i 1 0 6 8.09 1.5 -10 1
i . . 4 . 3.1 . [1/3]
i . . 3 . 3.4 . [1/6]
i . . 4 . 4.2 . [1/9]
i . . 5 . 6.1 . [1/12]
i . . 6 . 6.3 . [1/15]
</CsScore>
</CsoundSynthesizer>
You might ask: "Okay, where is the simplification? There are even more lines than before!" This is true, but this still represents better coding practice. The main benefit now is flexibility. Now we are able to realise any number of partials using the same instrument, with any amplitude, frequency and duration ratios. Using the Csound score abbreviations (for instance a dot for repeating the previous value in the same p-field), you can make great use of copy-and-paste, and focus just on what is changing from line to line.
Note that you are now calling one instrument multiple times in the creation of a single additive synthesis note, in fact, each instance of the instrument contributes just one partial to the additive tone. Calling multiple instances of one instrument in this way also represents good practice in Csound coding. We will discuss later how this end can be achieved in a more elegant way.
Creating Function Tables for Additive Synthesis
Before we continue, let us return to the first example and discuss a classic and abbreviated method for playing a number of partials. As we mentioned at the beginning, Fourier stated that any periodic oscillation can be described using a sum of simple sinusoids. If the single sinusoids are static (with no individual envelopes, durations or frequency fluctuations), the resulting waveform will be similarly static.
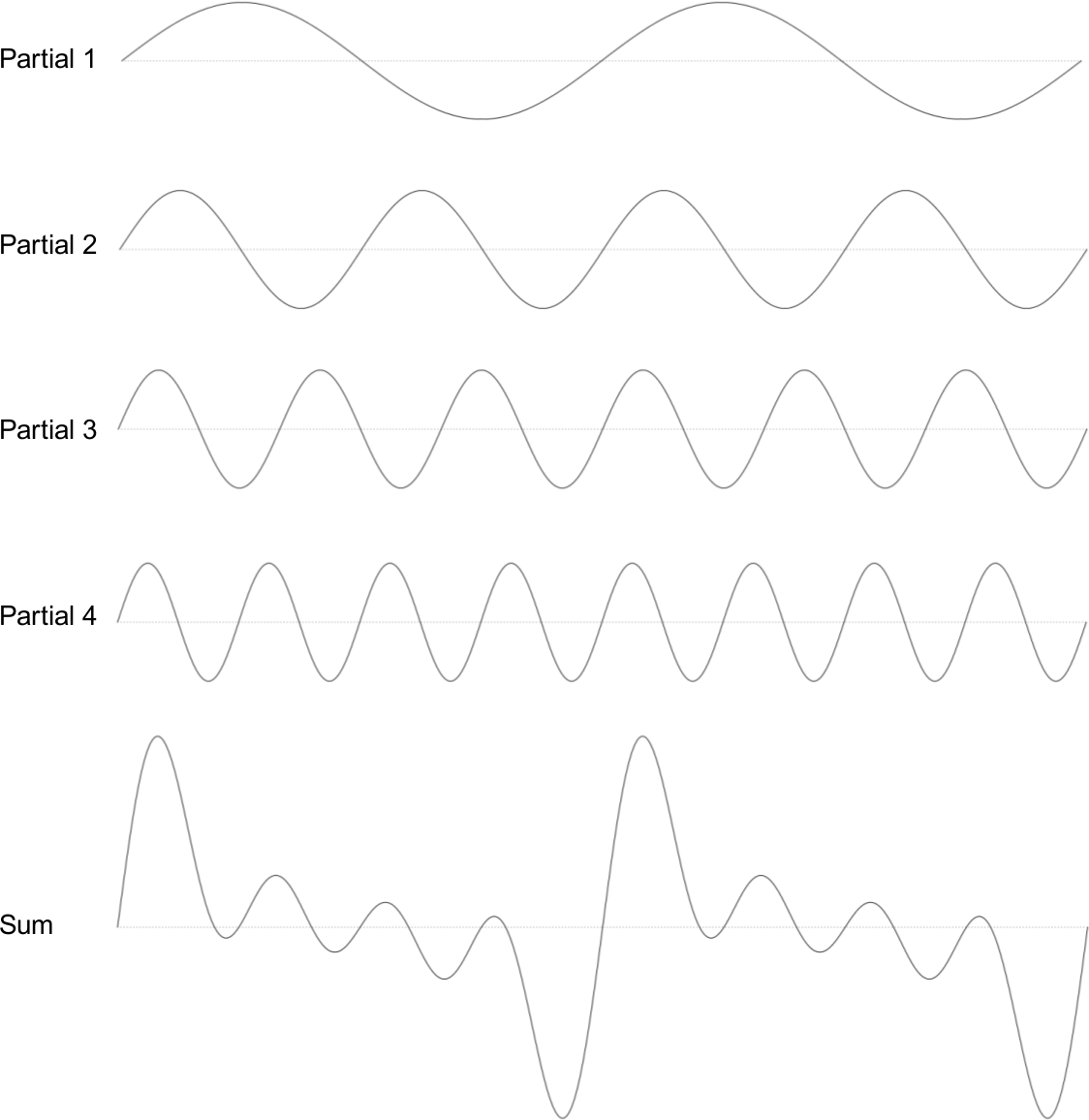
Above you see four sine waves, each with fixed frequency and amplitude relationships. These are then mixed together with the resulting waveform illustrated at the bottom (Sum). This then begs the question: why not simply calculate this composite waveform first, and then read it with just a single oscillator?
This is what some Csound GEN routines do. They compose the resulting shape of the periodic waveform, and store the values in a function table. GEN10 can be used for creating a waveform consisting of harmonically related partials. It form begins with the common GEN routine p-fields
<table number>, <creation time>, <size in points>, <GEN number>
following which you just have to define the relative strengths of the harmonics. GEN09 is more complex and allows you to also control the frequency multiplier and the phase (0-360°) of each partial. Thus we are able to reproduce the first example in a shorter (and computationally faster) form:
EXAMPLE 04A03_AddSynth_GEN.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;example by Andrés Cabrera and Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
giHarm ftgen 1, 0, 2^12, 10, 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8
giNois ftgen 2, 0, 2^12, 9, 100,1,0, 102,1/2,0, 110,1/3,0, \
123,1/4,0, 126,1/5,0, 131,1/6,0, 139,1/7,0, 141,1/8,0
instr 1
iBasFreq = cpspch(p4)
iTabFreq = p7 ;base frequency of the table
iBasFreq = iBasFreq / iTabFreq
iBaseAmp = ampdb(p5)
iFtNum = p6
aOsc poscil iBaseAmp, iBasFreq, iFtNum
aEnv linen aOsc, p3/4, p3, p3/4
outs aEnv, aEnv
endin
</CsInstruments>
<CsScore>
; pch amp table table base (Hz)
i 1 0 5 8.00 -10 1 1
i . 3 5 9.00 -14 . .
i . 5 8 9.02 -12 . .
i . 6 9 7.01 -12 . .
i . 7 10 6.00 -10 . .
s
i 1 0 5 8.00 -10 2 100
i . 3 5 9.00 -14 . .
i . 5 8 9.02 -12 . .
i . 6 9 7.01 -12 . .
i . 7 10 6.00 -10 . .
</CsScore>
</CsoundSynthesizer>
You maybe noticed that to store a waveform in which the partials are not harmonically related, the table must be constructed in a slightly special way (see table 'giNois'). If the frequency multipliers in our first example started with 1 and 1.02, the resulting period is actually very long. If the oscillator was playing at 100 Hz, the tone it would produce would actually contain partials at 100 Hz and 102 Hz. So you need 100 cycles from the 1.00 multiplier and 102 cycles from the 1.02 multiplier to complete one period of the composite waveform. In other words, we have to create a table which contains respectively 100 and 102 periods, instead of 1 and 1.02. Therefore the table frequencies will not be related to 1 as usual but instead to 100. This is the reason that we have to introduce a new parameter, iTabFreq, for this purpose. (N.B. In this simple example we could actually reduce the ratios to 50 and 51 as 100 and 102 share a common denominator of 2.)
This method of composing waveforms can also be used for generating four standard waveform shapes typically encountered in vintage synthesizers. An impulse wave can be created by adding a number of harmonics of the same strength. A sawtooth wave has the amplitude multipliers 1, 1/2, 1/3, ... for the harmonics. A square wave has the same multipliers, but just for the odd harmonics. A triangle can be calculated as 1 divided by the square of the odd partials, with swapping positive and negative values. The next example creates function tables with just the first ten partials for each of these waveforms.
EXAMPLE 04A04_Standard_waveforms.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giImp ftgen 1, 0, 4096, 10, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1
giSaw ftgen 2, 0, 4096, 10, 1,1/2,1/3,1/4,1/5,1/6,1/7,1/8,1/9,1/10
giSqu ftgen 3, 0, 4096, 10, 1, 0, 1/3, 0, 1/5, 0, 1/7, 0, 1/9, 0
giTri ftgen 4, 0, 4096, 10, 1, 0, -1/9, 0, 1/25, 0, -1/49, 0, 1/81, 0
instr 1
asig poscil .2, 457, p4
outs asig, asig
endin
</CsInstruments>
<CsScore>
i 1 0 3 1
i 1 4 3 2
i 1 8 3 3
i 1 12 3 4
</CsScore>
</CsoundSynthesizer>
Triggering Instrument Events for the Partials
Performing additive synthesis by designing partial strengths into function tables has the disadvantage that once a note has begun there is no way of varying the relative strengths of individual partials. There are various methods to circumvent the inflexibility of table-based additive synthesis such as morphing between several tables (for example by using the ftmorf opcode) or by filtering the result. Next we shall consider another approach: triggering one instance of a sub-instrument1 for each partial, and exploring the possibilities of creating a spectrally dynamic sound using this technique.
Let us return to the second instrument (04A02.csd) which had already made use of some abstractions and triggered one instrument instance for each partial. This was done in the score, but now we will trigger one complete note in one score line, not just one partial. The first step is to assign the desired number of partials via a score parameter. The next example triggers any number of partials using this one value:
EXAMPLE 04A05_Flexible_number_of_partials.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
instr 1 ;master instrument
inumparts = p4 ;number of partials
ibasfreq = 200 ;base frequency
ipart = 1 ;count variable for loop
;loop for inumparts over the ipart variable
;and trigger inumpartss instanes of the subinstrument
loop:
ifreq = ibasfreq * ipart
iamp = 1/ipart/inumparts
event_i "i", 10, 0, p3, ifreq, iamp
loop_le ipart, 1, inumparts, loop
endin
instr 10 ;subinstrument for playing one partial
ifreq = p4 ;frequency of this partial
iamp = p5 ;amplitude of this partial
aenv transeg 0, .01, 0, iamp, p3-0.1, -10, 0
apart poscil aenv, ifreq, giSine
outs apart, apart
endin
</CsInstruments>
<CsScore>
; number of partials
i 1 0 3 10
i 1 3 3 20
i 1 6 3 2
</CsScore>
</CsoundSynthesizer>
This instrument can easily be transformed to be played via a midi keyboard. In the next the midi key velocity will map to the number of synthesized partials played to implement a brightness control.
EXAMPLE 04A06_Play_it_with_Midi.csd
<CsoundSynthesizer>
<CsOptions>
-o dac -Ma
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
massign 0, 1 ;all midi channels to instr 1
instr 1 ;master instrument
ibasfreq cpsmidi ;base frequency
iampmid ampmidi 20 ;receive midi-velocity and scale 0-20
inparts = int(iampmid)+1 ;exclude zero
ipart = 1 ;count variable for loop
;loop for inparts over the ipart variable
;and trigger inparts instances of the sub-instrument
loop:
ifreq = ibasfreq * ipart
iamp = 1/ipart/inparts
event_i "i", 10, 0, 1, ifreq, iamp
loop_le ipart, 1, inparts, loop
endin
instr 10 ;subinstrument for playing one partial
ifreq = p4 ;frequency of this partial
iamp = p5 ;amplitude of this partial
aenv transeg 0, .01, 0, iamp, p3-.01, -3, 0
apart poscil aenv, ifreq, giSine
outs apart/3, apart/3
endin
</CsInstruments>
<CsScore>
f 0 3600
</CsScore>
</CsoundSynthesizer>
Although this instrument is rather primitive it is useful to be able to control the timbre in this way using key velocity. Let us continue to explore some other methods of creating parameter variation in additive synthesis.
User-controlled Random Variations in Additive Synthesis
Natural sounds exhibit constant movement and change in the parameters we have so far discussed. Even the best player or singer will not be able to play a note in the exact same way twice and within a tone, the partials will have some unsteadiness: slight waverings in the amplitudes and slight frequency fluctuations. In an audio programming environment like Csound, we can imitate these movements by employing random deviations. The boundaries of random deviations must be adjusted as carefully. Exaggerate them and the result will be unnatural or like a bad player. The rates or speeds of these fluctuations will also need to be chosen carefully and sometimes we need to modulate the rate of modulation in order to achieve naturalness.
Let us start with some random deviations in our subinstrument. The following parameters can be affected:
- The frequency of each partial can be slightly detuned. The range of this possible maximum detuning can be set in cents (100 cent = 1 semitone).
- The amplitude of each partial can be altered relative to its default value. This alteration can be measured in decibels (dB).
- The duration of each partial can be made to be longer or shorter than the default value. Let us define this deviation as a percentage. If the expected duration is five seconds, a maximum deviation of 100% will mean a resultant value of between half the duration (2.5 sec) and double the duration (10 sec).
The following example demonstrates the effect of these variations. As a base - and as a reference to its author - we take as our starting point, the 'bell-like' sound created by Jean-Claude Risset in his 'Sound Catalogue'.2
EXAMPLE 04A07_Risset_variations.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
;frequency and amplitude multipliers for 11 partials of Risset's bell
giFqs ftgen 0, 0, -11,-2,.56,.563,.92, .923,1.19,1.7,2,2.74, \
3,3.74,4.07
giAmps ftgen 0, 0, -11, -2, 1, 2/3, 1, 1.8, 8/3, 1.46, 4/3, 4/3, 1, 4/3
giSine ftgen 0, 0, 2^10, 10, 1
seed 0
instr 1 ;master instrument
ibasfreq = 400
ifqdev = p4 ;maximum freq deviation in cents
iampdev = p5 ;maximum amp deviation in dB
idurdev = p6 ;maximum duration deviation in %
indx = 0 ;count variable for loop
loop:
ifqmult tab_i indx, giFqs ;get frequency multiplier from table
ifreq = ibasfreq * ifqmult
iampmult tab_i indx, giAmps ;get amp multiplier
iamp = iampmult / 20 ;scale
event_i "i", 10, 0, p3, ifreq, iamp, ifqdev, iampdev, idurdev
loop_lt indx, 1, 11, loop
endin
instr 10 ;subinstrument for playing one partial
;receive the parameters from the master instrument
ifreqnorm = p4 ;standard frequency of this partial
iampnorm = p5 ;standard amplitude of this partial
ifqdev = p6 ;maximum freq deviation in cents
iampdev = p7 ;maximum amp deviation in dB
idurdev = p8 ;maximum duration deviation in %
;calculate frequency
icent random -ifqdev, ifqdev ;cent deviation
ifreq = ifreqnorm * cent(icent)
;calculate amplitude
idb random -iampdev, iampdev ;dB deviation
iamp = iampnorm * ampdb(idb)
;calculate duration
idurperc random -idurdev, idurdev ;duration deviation (%)
iptdur = p3 * 2^(idurperc/100)
p3 = iptdur ;set p3 to the calculated value
;play partial
aenv transeg 0, .01, 0, iamp, p3-.01, -10, 0
apart poscil aenv, ifreq, giSine
outs apart, apart
endin
</CsInstruments>
<CsScore>
; frequency amplitude duration
; deviation deviation deviation
; in cent in dB in %
;;unchanged sound (twice)
r 2
i 1 0 5 0 0 0
s
;;slight variations in frequency
r 4
i 1 0 5 25 0 0
;;slight variations in amplitude
r 4
i 1 0 5 0 6 0
;;slight variations in duration
r 4
i 1 0 5 0 0 30
;;slight variations combined
r 6
i 1 0 5 25 6 30
;;heavy variations
r 6
i 1 0 5 50 9 100
</CsScore>
</CsoundSynthesizer>
In midi-triggered descendant of this instrument, we could - as one of many possible options - vary the amount of possible random variation according to the key velocity so that a key pressed softly plays the bell-like sound as described by Risset but as a key is struck with increasing force the sound produced will be increasingly altered.
EXAMPLE 04A08_Risset_played_by_Midi.csd
<CsoundSynthesizer>
<CsOptions>
-o dac -Ma
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
;frequency and amplitude multipliers for 11 partials of Risset's bell
giFqs ftgen 0, 0, -11, -2, .56,.563,.92,.923,1.19,1.7,2,2.74,3,\
3.74,4.07
giAmps ftgen 0, 0, -11, -2, 1, 2/3, 1, 1.8, 8/3, 1.46, 4/3, 4/3, 1,\
4/3
giSine ftgen 0, 0, 2^10, 10, 1
seed 0
massign 0, 1 ;all midi channels to instr 1
instr 1 ;master instrument
;;scale desired deviations for maximum velocity
;frequency (cent)
imxfqdv = 100
;amplitude (dB)
imxampdv = 12
;duration (%)
imxdurdv = 100
;;get midi values
ibasfreq cpsmidi ;base frequency
iampmid ampmidi 1 ;receive midi-velocity and scale 0-1
;;calculate maximum deviations depending on midi-velocity
ifqdev = imxfqdv * iampmid
iampdev = imxampdv * iampmid
idurdev = imxdurdv * iampmid
;;trigger subinstruments
indx = 0 ;count variable for loop
loop:
ifqmult tab_i indx, giFqs ;get frequency multiplier from table
ifreq = ibasfreq * ifqmult
iampmult tab_i indx, giAmps ;get amp multiplier
iamp = iampmult / 20 ;scale
event_i "i", 10, 0, 3, ifreq, iamp, ifqdev, iampdev, idurdev
loop_lt indx, 1, 11, loop
endin
instr 10 ;subinstrument for playing one partial
;receive the parameters from the master instrument
ifreqnorm = p4 ;standard frequency of this partial
iampnorm = p5 ;standard amplitude of this partial
ifqdev = p6 ;maximum freq deviation in cents
iampdev = p7 ;maximum amp deviation in dB
idurdev = p8 ;maximum duration deviation in %
;calculate frequency
icent random -ifqdev, ifqdev ;cent deviation
ifreq = ifreqnorm * cent(icent)
;calculate amplitude
idb random -iampdev, iampdev ;dB deviation
iamp = iampnorm * ampdb(idb)
;calculate duration
idurperc random -idurdev, idurdev ;duration deviation (%)
iptdur = p3 * 2^(idurperc/100)
p3 = iptdur ;set p3 to the calculated value
;play partial
aenv transeg 0, .01, 0, iamp, p3-.01, -10, 0
apart poscil aenv, ifreq, giSine
outs apart, apart
endin
</CsInstruments>
<CsScore>
f 0 3600
</CsScore>
</CsoundSynthesizer>
Whether you can play examples like this in realtime will depend on the power of your computer. Have a look at chapter 2D (Live Audio) for tips on getting the best possible performance from your Csound orchestra.
In the next example we shall use additive synthesis to make a kind of a wobble bass. It starts as a bass sound, then evolves into something else, and then returns to being a bass sound again. We will first generate all the inharmonic partials with a loop. Harmonic partials are arithmetic, we add the same value to one partial to get the next. In this example we will instead use geometric partials, we will multiply one partial with a certain number (kfreqmult) to derive the next partial frequency and so on. This number will not be constant, but will be generated by a sine oscillator. This is frequency modulation. Finally some randomness is added to create a more interesting sound, and a chorus effect is also added to make the sound more 'fat'. The exponential function, exp, is used when deriving frequencies because if we move upwards in common musical scales, then the frequencies grow exponentially.
EXAMPLE 04A09_Wobble_bass.csd
<CsoundSynthesizer> ; Wobble bass made using additive synthesis
<CsOptions> ; and frequency modulation
-odac
</CsOptions>
<CsInstruments>
; Example by Bjørn Houdorf, March 2013
sr = 44100
ksmps = 1
nchnls = 2
0dbfs = 1
instr 1
kamp = 24 ; Amplitude
kfreq expseg p4, p3/2, 50*p4, p3/2, p4 ; Base frequency
iloopnum = p5 ; Number of all partials generated
alyd1 init 0
alyd2 init 0
seed 0
kfreqmult oscili 1, 2, 1
kosc oscili 1, 2.1, 1
ktone randomh 0.5, 2, 0.2 ; A random input
icount = 1
loop: ; Loop to generate partials to additive synthesis
kfreq = kfreqmult * kfreq
atal oscili 1, 0.5, 1
apart oscili 1, icount*exp(atal*ktone) , 1 ; Modulate each partials
anum = apart*kfreq*kosc
asig1 oscili kamp, anum, 1
asig2 oscili kamp, 1.5*anum, 1 ; Chorus effect to make the sound more "fat"
asig3 oscili kamp, 2*anum, 1
asig4 oscili kamp, 2.5*anum, 1
alyd1 = (alyd1 + asig1+asig4)/icount ;Sum of partials
alyd2 = (alyd2 + asig2+asig3)/icount
loop_lt icount, 1, iloopnum, loop ; End of loop
outs alyd1, alyd2 ; Output generated sound
endin
</CsInstruments>
<CsScore>
f1 0 128 10 1
i1 0 60 110 50
e
</CsScore>
</CsoundSynthesizer>
gbuzz, buzz and GEN11
gbuzz is useful for creating additive tones made of harmonically related cosine waves. Rather than define attributes for every partial individually, gbuzz allows us to define parameters that describe the entire additive tone in a more general way: specifically the number of partials in the tone, the partial number of the lowest partial present and an amplitude coefficient multipler, which shifts the peak of spectral energy in the tone. Although number of harmonics (knh) and lowest hamonic (klh) are k-rate arguments, they are only interpreted as integers by the opcode; therefore changes from integer to integer will result in discontinuities in the output signal. The amplitude coefficient multiplier allows for smooth spectral modulations however. Although we lose some control of individual partials using gbuzz, we gain by being able to nimbly sculpt the spectrum of the tone it produces.
In the following example a 100Hz tone is created, in which the number of partials it contains rises from 1 to 20 across its 8 second duration. A spectrogram/sonogram displays how this manifests spectrally. A linear frequency scale is employed in the spectrogram so that harmonic partials appear equally spaced.
EXAMPLE 04A10_gbuzz.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
; a cosine wave
gicos ftgen 0, 0, 2^10, 11, 1
instr 1
knh line 1, p3, 20 ; number of harmonics
klh = 1 ; lowest harmonic
kmul = 1 ; amplitude coefficient multiplier
asig gbuzz 1, 100, knh, klh, kmul, gicos
outs asig, asig
endin
</CsInstruments>
<CsScore>
i 1 0 8
e
</CsScore>
</CsoundSynthesizer>

The total number of partials only reaches 19 because the line function only reaches 20 at the very conclusion of the note.
In the next example the number of partials contained within the tone remains constant but the partial number of the lowest partial rises from 1 to 20.
EXAMPLE 04A11_gbuzz_partials_rise.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
; a cosine wave
gicos ftgen 0, 0, 2^10, 11, 1
instr 1
knh = 20
klh line 1, p3, 20
kmul = 1
asig gbuzz 1, 100, knh, klh, kmul, gicos
outs asig, asig
endin
</CsInstruments>
<CsScore>
i 1 0 8
e
</CsScore>
</CsoundSynthesizer>
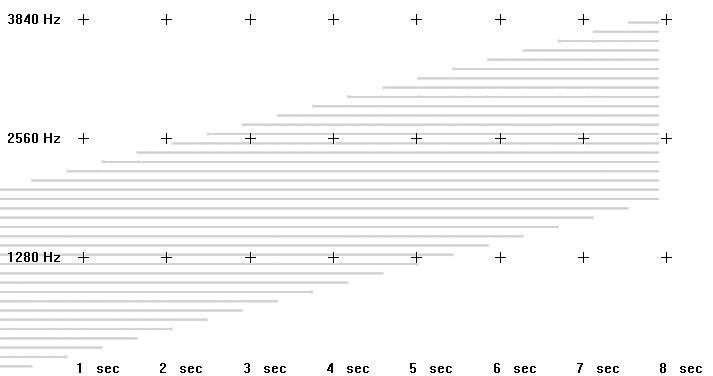
In the spectrogram it can be seen how, as lowermost partials are removed, additional partials are added at the top of the spectrum. This is because the total number of partials remains constant at 20.
In the final gbuzz example the amplitude coefficient multiplier rises from 0 to 2. It can be heard (and seen in the spectrogram) how, when this value is zero, emphasis is on the lowermost partial and when this value is 2, emphasis is on the uppermost partial.
EXAMPLE 04A12_gbuzz_amp_coeff_rise.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
; a cosine wave
gicos ftgen 0, 0, 2^10, 11, 1
instr 1
knh = 20
klh = 1
kmul line 0, p3, 2
asig gbuzz 1, 100, knh, klh, kmul, gicos
outs asig, asig
endin
</CsInstruments>
<CsScore>
i 1 0 8
e
</CsScore>
</CsoundSynthesizer>
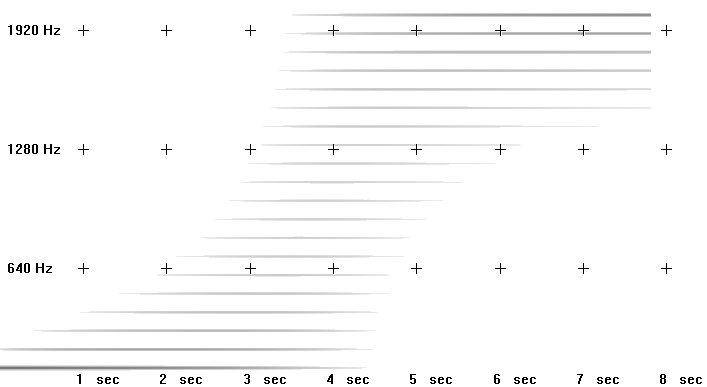
buzz is a simplified version of gbuzz with fewer parameters – it does not provide for modulation of the lowest partial number and amplitude coefficient multiplier.
GEN11 creates a function table waveform using the same parameters as gbuzz. If a gbuzz tone is required but no performance time modulation of its parameters is needed, GEN11 may provide a more efficient option. GEN11 also opens the possibility of using its waveforms in a variety of other opcodes. gbuzz, buzz and GEN11 may also prove useful as a source for subtractive synthesis.
Additional Interesting Opcodes for Additive Synthesis
hsboscil
The opcode hsboscil offers an interesting method of additive synthesis in which all partials are spaced an octave apart. Whilst this may at first seems limiting, it does offer simple means for morphing the precise make up of its spectrum. It can be thought of as producing a sound spectrum that extends infinitely above and below the base frequency. Rather than sounding all of the resultant partials simultaneously, a window (typically a Hanning window) is placed over the spectrum, masking it so that only one or several of these partials sound at any one time. The user can shift the position of this window up or down the spectrum at k-rate and this introduces the possibility of spectral morphing. hsbosil refers to this control as 'kbrite'. The width of the window can be specified (but only at i-time) using its 'iOctCnt' parameter. The entire spectrum can also be shifted up or down, independent of the location of the masking window using the 'ktone' parameter, which can be used to create a 'Risset glissando'-type effect. The sense of the interval of an octave between partials tends to dominate but this can be undermined through the use of frequency shifting or by using a waveform other than a sine wave as the source waveform for each partial.
In the next example, instrument 1 demonstrates the basic sound produced by hsboscil whilst randomly modulating the location of the masking window (kbrite) and the transposition control (ktone). Instrument 2 introduces frequency shifting (through the use of the hilbert opcode) which adds a frequency value to all partials thereby warping the interval between partials. Instrument 3 employs a more complex waveform (pseudo-inharmonic) as the source waveform for the partials.
EXAMPLE 04A13_hsboscil.csd
<CsoundSynthesizer>
<CsOptions>
--env:SSDIR+=../SourceMaterials -odac
</CsOptions>
<CsInstruments>
;example by iain mccurdy
sr = 44100
ksmps = 32
0dbfs = 1
nchnls = 2
giSine ftgen 0, 0, 2^10, 10, 1
; hanning window
giWindow ftgen 0, 0, 1024, -19, 1, 0.5, 270, 0.5
; a complex pseudo inharmonic waveform (partials scaled up X 100)
giWave ftgen 0, 0, 262144, 9, 100,1.000,0, 278,0.500,0, 518,0.250,0,
816,0.125,0, 1166,0.062,0, 1564,0.031,0, 1910,0.016,0
instr 1 ; demonstration of hsboscil
kAmp = 0.3
kTone rspline -1,1,0.05,0.2 ; randomly shift spectrum up and down
kBrite rspline -1,3,0.4,2 ; randomly shift masking window up and down
iBasFreq = 200 ; base frequency
iOctCnt = 3 ; width of masking window
aSig hsboscil kAmp, kTone, kBrite, iBasFreq, giSine, giWindow, iOctCnt
out aSig, aSig
endin
instr 2 ; frequency shifting added
kAmp = 0.3
kTone = 0 ; spectrum remains static this time
kBrite rspline -2,5,0.4,2 ; randomly shift masking window up and down
iBasFreq = 75 ; base frequency
iOctCnt = 6 ; width of masking window
aSig hsboscil kAmp, kTone, kBrite, iBasFreq, giSine, giWindow, iOctCnt
; frequency shift the sound
kfshift = -357 ; amount to shift the frequency
areal,aimag hilbert aSig ; hilbert filtering
asin poscil 1, kfshift, giSine, 0 ; modulating signals
acos poscil 1, kfshift, giSine, 0.25
aSig = (areal*acos) - (aimag*asin) ; frequency shifted signal
out aSig, aSig
endin
instr 3 ; hsboscil using a complex waveform
kAmp = 0.3
kTone rspline -1,1,0.05,0.2 ; randomly shift spectrum up and down
kBrite rspline -3,3,0.1,1 ; randomly shift masking window
iBasFreq = 200
aSig hsboscil kAmp, kTone, kBrite, iBasFreq/100, giWave, giWindow
aSig2 hsboscil kAmp,kTone, kBrite, (iBasFreq*1.001)/100, giWave, giWindow
out aSig+aSig2, aSig+aSig2 ; mix signal with 'detuned' version
endin
</CsInstruments>
<CsScore>
i 1 0 14
i 2 15 14
i 3 30 14
e
</CsScore>
</CsoundSynthesizer>
Additive synthesis can still be an exciting way of producing sounds. It offers the user a level of control that other methods of synthesis simply cannot match. It also provides an essential workbench for learning about acoustics and spectral theory as related to sound.