CSOUND
INTRODUCTION
LEASE READ THE NEW VERSION OF THE CSOUND FLOSS MANUAL HERE:
https://flossmanual.csound.com/
THIS VERSION HAS REVISED TEXT AND ALL EXAMPLES CAN BE EXECUTED IN THE BROWSER!

| Read the Online Version |
Read the EPUB Version |
| Read the PDF Version |
Read in Open Office |
Csound is one of the best known and longest established programs in the field of audio programming. It was developed in the mid-1980s at the Massachusetts Institute of Technology (MIT) by Barry Vercoe but Csound's history lies even deeper within the roots of computer music: it is a direct descendant of the oldest computer program for sound synthesis, 'MusicN', by Max Mathews. Csound is free and open source, distributed under the LGPL licence, and it is maintained and expanded by a core of developers with support from a wider global community.
Csound has been growing for 30 years. There is rarely anything related to audio that you cannot do with Csound. You can work by rendering offline, or in real-time by processing live audio and synthesizing sound on the fly. You can control Csound via MIDI, OSC, through a network, within a browser or via the Csound API (Application Programming Interface). Csound will run on all major platforms, on phones, tablets and tinyware computers. In Csound you will find the widest collection of tools for sound synthesis and sound modification, arguably offering a superset of features offered by similar software and with an unrivaled audio precision.
Csound is simultaneously both 'old school' and 'new school'.
Is Csound difficult to learn? Generally speaking, graphical audio programming languages like Pure Data,1 Max or Reaktor are easier to learn than text-coded audio programming languages such as Csound or SuperCollider. In Pd, Max or Reaktor you cannot make a typo which produces an error that you do not understand. You program without being aware that you are programming. The user experience mirrors that of patching together various devices in a studio. This is a fantastically intuitive approach but when you deal with more complex projects, a text-based programming language is often easier to use and debug, and many people prefer to program by typing words and sentences rather than by wiring symbols together using the mouse.
Yet Csound can straddle both approaches: it is also very easy to use Csound as an audio engine inside Pd or Max. Have a look at the chapter Csound in Other Applications for further information.
Amongst text-based audio programming languages, Csound is arguably the simplest. You do not need to know any specific programming techniques or to be a computer scientist. The basics of the Csound language are a straightforward transfer of the signal flow paradigm to text.
For example, to create a 400 Hz sine oscillator with an amplitude of 0.2, this is the signal flow:
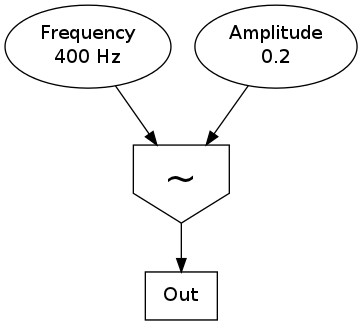
Here is a possible transformation of the signal graph into Csound code:
instr Sine
aSig poscil 0.2, 400
out aSig
endin
The oscillator is represented by the opcode poscil and receives its input arguments on the right-hand side. These are amplitude (0.2) and frequency (400). It produces an audio signal called aSig at the left side which is in turn the input of the second opcode out. The first and last lines encase these connections inside an instrument called Sine.
With the release of Csound version 6, it is possible to write the same code in an even more condensed fashion using so-called "functional syntax", as shown below:2
instr Sine
out poscil(0.2, 400)
endin
It is often difficult to find up to date resources that show and explain what is possible with Csound. Documentation and tutorials produced by developers and experienced users tend to be scattered across many different locations. This issue was one of the main motivations for producing this manual; to facilitate a flow between the knowledge of contemporary Csound users and those wishing to learn more about Csound.
More than 15 years after the milestone of Richard Boulanger's Csound Book, the Csound FLOSS Manual is intended to offer an easy-to-understand introduction and to provide a centre of up to date information about the many features of Csound, not as detailed and as in depth as the Csound Book, but including new information and sharing this knowledge with the wider Csound community.
Throughout this manual we will attempt to maintain a balance between providing users with knowledge of most of the important aspects of Csound whilst also remaining concise and simple enough to avoid overwhelming the reader through the shear number of possibilities offered by Csound. Frequently this manual will link to other more detailed resources such as the Canonical Csound Reference Manual, the main support documentation provided by the Csound developers and associated community over the years, and the Csound Journal (edited by James Hearon and Iain McCurdy), a roughly quarterly online publication with many great Csound-related articles.
We hope you enjoy reading this textbook and wish you happy Csounding!
- more commonly known as Pd - see the Pure Data FLOSS Manual for further information^
- See chapter 03I about Functional Syntax^
HOW TO USE THIS MANUAL
The goal of this manual is to provide a readable introduction to Csound. In no way is it meant as a replacement for the Canonical Csound Reference Manual. It is intended as an introduction-tutorial-reference hybrid, gathering together the most important information you will need to work with Csound in a variety of situations. In many places links are provided to other resources such as The Canonical Csound Reference Manual, the Csound Journal, example collections and more.
It is not necessary to read each chapter in sequence, feel free to jump to any chapter that interests you, although bear in mind that occasionally a chapter may make reference to a previous one.
If you are new to Csound, the QUICK START chapter will be the best place to go to help you get started. BASICS provides a general introduction to key concepts about digital sound, vital to understanding how Csound deals with audio. The CSOUND LANGUAGE chapter provides greater detail about how Csound works and how to work with Csound.
SOUND SYNTHESIS introduces various methods of creating sound from scratch and SOUND MODIFICATION describes various methods of transforming sounds that already exist. SAMPLES outlines various ways you can record and playback audio samples in Csound; an area that might be of particular interest to those intent on using Csound as a real-time performance instrument. The MIDI and OPEN SOUND CONTROL chapters focus on different methods of controlling Csound using external software or hardware. The final chapters introduce various front-ends that can be used to interface with the Csound engine and Csound's communication with other applications.
If you would like to know more about a topic, and in particular about the use of any opcode, please refer first to the Canonical Csound Reference Manual.
All files - examples and audio files - can be downloaded at www.csound-tutorial.net. If you use CsoundQt, you can find all the examples in CsoundQt's examples menu under "Floss Manual Examples". When learning Csound (or any other programming language), you may find it beneficial to type the examples out by hand as it will help you to memorise Csound's syntax as well as how to use its opcodes. The more familiar you become with typing out Csound code, the more proficient you will become at implementing your own ideas from low level principles; your focus will shift from the code itself to the musical idea behind the code.
Like other audio tools, Csound can produce an extreme dynamic range (before considering Csound's ability to implement compression and limiting). Be careful when you run the examples! Set the volume on your amplifier low to start with and take special care when using headphones.
You can help to improve this manual either by reporting bugs or by sending requests for new topics or by joining as a writer. Just contact one of the maintainers (see ON THIS RELEASE).
Some issues of this textbook can be ordered as a print-on-demand hard copy at www.lulu.com. Just use Lulu's search utility and look for "Csound".
ON THIS (6th) RELEASE
A year on from the 5th release, this release adds some exciting new sections as well as a number of chapter augmentations and necessary updates. Notable are Michael Gogins' Chapter on running Csound within a browser using HTML5 technology, Victor Lazarrini's and Ed Costello's explanations about Web based Csound, and a new chapter describing the pairing of Csound with the Haskell programming language.
Thanks to all contributors to this release.
What's new in this Release
- Added a section about the necessity of explicit initialization of k-variables for multiple calls of an instrument or UDO in chapter 03A Initialization and Performance Pass (examples 8-10).
- Added a section about the while/until loop in chapter 03C Control Structures.
- Expanded chapter 03D Function Tables, adding descriptions of GEN 08, 16, 19 and 30.
- Small additions in chapter 03E Arrays.
- Some additions and a new section to help using the different opcodes (schedule, event, scoreline etc) in 03F Live Events.
- Added a chapter 03I about Functional Syntax.
- Added examples and descriptions for the powershape and distort opcodes in the chapter 04 Sound Synthesis: Waveshaping.
- Expanded chapter 05A Envelopes, principally to incorporate descriptions of transeg and cosseg.
- Added chapter 05L about methods of amplitude and pitch tracking in Csound.
- Added example to illustrate the recording of controller data to the chapter 07C Working with Controllers at the request of Menno Knevel.
- Chapter 10B Cabbage has been updated and attention drawn to some of its newest features.
- Chapter 10F Web Based Csound has now a description about how to use Csound via UDP and about pNaCl Csound (written by Victor Lazzarini). The section about Csound as a Javascript Library (using Emscripten) in the same chapter has been updated by Ed Costello.
- Refactored chapter 12A about The Csound API for Csound6 and added a section about the use of Foreign Function Interfaces (FFI) (written by François Pinot).
- Added chapter 12G about Csound and Haskell (written by Anton Kholomiov).
- Added chapter 12H about Csound and HMTL, also explaining the usage of HTML5 Widgets (written by Michael Gogins).
The examples in this book are included in CsoundQt (Examples > FLOSS Manual Examples). Even the examples which require external files should now work out of the box.
If you would like to refer to previous releases, you can find them at http://files.csound-tutorial.net/floss_manual. Also here are all the current csd files and audio samples.
Berlin, March 2015
Iain McCurdy and Joachim Heintz

License
All chapters are copyright of the authors (see below). Unless otherwise stated all chapters in this manual are licensed with GNU General Public License version 2.
This documentation is free documentation; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation; either version 2 of the License, or (at your option) any later version.
This documentation is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
You should have received a copy of the GNU General Public License along with this documentation; if not, write to the Free Software Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA 02110-1301, USA.
Authors
Note that this book is a collective effort, so some of the contributors may not have been quoted correctly. If you are one of them, please contact us, or simply add your name for credit in the appropriate place.
INTRODUCTION
PREFACE
Joachim Heintz, Andres Cabrera, Alex Hofmann, Iain McCurdy, Alexandre Abrioux
HOW TO USE THIS MANUAL
Joachim Heintz, Andres Cabrera, Iain McCurdy, Alexandre Abrioux
01 BASICS
A. DIGITAL AUDIO
Alex Hofmann, Rory Walsh, Iain McCurdy, Joachim Heintz
B. PITCH AND FREQUENCY
Rory Walsh, Iain McCurdy, Joachim Heintz
C. INTENSITIES
Joachim Heintz
D. RANDOM
Joachim Heintz, Martin Neukom, Iain McCurdy
02 QUICK START
A. MAKE CSOUND RUN
Alex Hofmann, Joachim Heintz, Andres Cabrera, Iain McCurdy, Jim Aikin, Jacques Laplat, Alexandre Abrioux, Menno Knevel
B. CSOUND SYNTAX
Alex Hofmann, Joachim Heintz, Andres Cabrera, Iain McCurdy
C. CONFIGURING MIDI
Andres Cabrera, Joachim Heintz, Iain McCurdy
D. LIVE AUDIO
Alex Hofmann, Andres Cabrera, Iain McCurdy, Joachim Heintz
E. RENDERING TO FILE
Joachim Heintz, Alex Hofmann, Andres Cabrera, Iain McCurdy
03 CSOUND LANGUAGE
A. INITIALIZATION AND PERFORMANCE PASS
Joachim Heintz
B. LOCAL AND GLOBAL VARIABLES
Joachim Heintz, Andres Cabrera, Iain McCurdy
C. CONTROL STRUCTURES
Joachim Heintz
D. FUNCTION TABLES
Joachim Heintz, Iain McCurdy
E. ARRAYS
Joachim Heintz
F. LIVE CSOUND
Joachim Heintz, Iain McCurdy
G. USER DEFINED OPCODES
Joachim Heintz
H. MACROS
Iain McCurdy
I. FUNCTIONAL SYNTAX
Joachim Heintz
04 SOUND SYNTHESIS
A. ADDITIVE SYNTHESIS
Andres Cabrera, Joachim Heintz, Bjorn Houdorf
B. SUBTRACTIVE SYNTHESIS
Iain McCurdy
C. AMPLITUDE AND RINGMODULATION
Alex Hofman
D. FREQUENCY MODULATION
Alex Hofmann, Bjorn Houdorf
E. WAVESHAPING
Joachim Heintz, Iain McCurdy
F. GRANULAR SYNTHESIS
Iain McCurdy
G. PHYSICAL MODELLING
Joachim Heintz, Iain McCurdy, Martin Neukom
H. SCANNED SYNTHESIS
Christopher Saunders
05 SOUND MODIFICATION
A. ENVELOPES
Iain McCurdy
B. PANNING AND SPATIALIZATION
Iain McCurdy, Joachim Heintz
C. FILTERS
Iain McCurdy
D. DELAY AND FEEDBACK
Iain McCurdy
E. REVERBERATION
Iain McCurdy
F. AM / RM / WAVESHAPING
Alex Hofmann, Joachim Heintz
G. GRANULAR SYNTHESIS
Iain McCurdy, Oeyvind Brandtsegg, Bjorn Houdorf
H. CONVOLUTION
Iain McCurdy
I. FOURIER ANALYSIS / SPECTRAL PROCESSING
Joachim Heintz
K. ANALYSIS TRANSFORMATION SYNTHESIS
Oscar Pablo di Liscia
L. AMPLITUDE AND PITCH TRACKING
Iain McCurdy
06 SAMPLES
A. RECORD AND PLAY SOUNDFILES
Iain McCurdy, Joachim Heintz
B. RECORD AND PLAY BUFFERS
Iain McCurdy, Joachim Heintz, Andres Cabrera
07 MIDI
A. RECEIVING EVENTS BY MIDIIN
Iain McCurdy
B. TRIGGERING INSTRUMENT INSTANCES
Joachim Heintz, Iain McCurdy
C. WORKING WITH CONTROLLERS
Iain McCurdy
D. READING MIDI FILES
Iain McCurdy
E. MIDI OUTPUT
Iain McCurdy
08 OTHER COMMUNICATION
A. OPEN SOUND CONTROL
Alex Hofmann
B. CSOUND AND ARDUINO
Iain McCurdy
09 CSOUND IN OTHER APPLICATIONS
A. CSOUND IN PD
Joachim Heintz, Jim Aikin
B. CSOUND IN MAXMSP
Davis Pyon
C. CSOUND IN ABLETON LIVE
Rory Walsh
D. CSOUND AS A VST PLUGIN
Rory Walsh
10 CSOUND FRONTENDS
CSOUNDQT
Andrés Cabrera, Joachim Heintz, Peiman Khosravi
CABBAGE
Rory Walsh, Menno Knevel, Iain McCurdy
BLUE
Steven Yi, Jan Jacob Hofmann
WINXOUND
Stefano Bonetti, Menno Knevel
CSOUND VIA TERMINAL
Iain McCurdy
WEB BASED CSOUND
Victor Lazzarini, Iain McCurdy, Ed Costello
11 CSOUND UTILITIES
CSOUND UTILITIES
Iain McCurdy
12 CSOUND AND OTHER PROGRAMMING LANGUAGES
A. THE CSOUND API
François Pinot, Rory Walsh
B. PYTHON INSIDE CSOUND
Andrés Cabrera, Joachim Heintz, Jim Aikin
C. PYTHON IN CSOUNDQT
Tarmo Johannes, Joachim Heintz
D. LUA IN CSOUND
E. CSOUND IN IOS
Nicholas Arner, Nikhil Singh, Richard Boulanger
F. CSOUND ON ANDROID
Michael Gogins
G. CSOUND AND HASKELL
Anton Kholomiov
H. CSOUND AND HTML
Michael Gogins
13 EXTENDING CSOUND
EXTENDING CSOUND
Victor Lazzarini
OPCODE GUIDE
OVERVIEW
Joachim Heintz, Iain McCurdy
SIGNAL PROCESSING I
Joachim Heintz, Iain McCurdy
SIGNAL PROCESSING II
Joachim Heintz, Iain McCurdy
DATA
Joachim Heintz, Iain McCurdy
REALTIME INTERACTION
Joachim Heintz, Iain McCurdy
INSTRUMENT CONTROL
Joachim Heintz, Iain McCurdy
MATH, PYTHON/SYSTEM, PLUGINS
Joachim Heintz, Iain McCurdy
APPENDIX
GLOSSARY
Joachim Heintz, Iain McCurdy
LINKS
Joachim Heintz, Stefano Bonetti
METHODS OF WRITING CSOUND SCORES
Iain McCurdy, Joachim Heintz, Jacob Joaquin, Menno Knevel
V.1 - Final Editing Team in March 2011:
Joachim Heintz, Alex Hofmann, Iain McCurdy
V.2 - Final Editing Team in March 2012:
Joachim Heintz, Iain McCurdy
V.3 - Final Editing Team in March 2013:
Joachim Heintz, Iain McCurdy
V.4 - Final Editing Team in September 2013:
Joachim Heintz, Alexandre Abrioux
V.5 - Final Editing Team in March 2014:
Joachim Heintz, Iain McCurdy
V.6 - Final Editing Team March-June 2015:
Joachim Heintz, Iain McCurdy
Free manuals for free software
01 BASICS
DIGITAL AUDIO
At a purely physical level, sound is simply a mechanical disturbance of a medium. The medium in question may be air, solid, liquid, gas or a combination of several of these. This disturbance in the medium causes molecules to move back and forth in a spring-like manner. As one molecule hits the next, the disturbance moves through the medium causing sound to travel. These so called compressions and rarefactions in the medium can be described as sound waves. The simplest type of waveform, describing what is referred to as 'simple harmonic motion', is a sine wave.
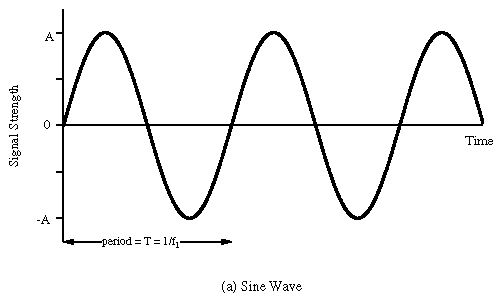
Each time the waveform signal goes above 0 the molecules are in a state of compression meaning that each molecule within the waveform disturbance is pushing into its neighbour. Each time the waveform signal drops below 0 the molecules are in a state of rarefaction meaning the molecules are pulling away from thier neighbours. When a waveform shows a clear repeating pattern, as in the case above, it is said to be periodic. Periodic sounds give rise to the sensation of pitch.
Elements of a Sound Wave
Periodic waves have four common parameters, and each of the four parameters affects the way we perceive sound.
-
Period: This is the length of time it takes for a waveform to complete one cycle. This amount of time is referred to as t
-
Wavelength: the distance it takes for a wave to complete one full period. This is usually measured in meters.
-
Frequency: the number of cycles or periods per second. Frequency is measured in Hertz. If a sound has a frequency of 440Hz it completes 440 cycles every second. Given a frequency, one can easily calculate the period of any sound. Mathematically, the period is the reciprocal of the frequency (and vice versa). In equation form this is expressed as follows.
Frequency = 1/Period Period = 1/Frequency
Therefore the frequency is the inverse of the period, so a wave of 100 Hz frequency has a period of 1/100 or 0.01 secs, likewise a frequency of 256Hz has a period of 1/256, or 0.004 secs. To calculate the wavelength of a sound in any given medium we can use the following equation:
Wavelength = Velocity/Frequency
Humans can hear frequencies from 20Hz to 20000Hz (although this can differ dramatically from individual to individual and the upper limit will decay with age). You can read more about frequency in the next chapter.
-
Phase: This is the starting point of a waveform. The starting point along the Y-axis of our plotted waveform is not always zero. This can be expressed in degrees or in radians. A complete cycle of a waveform will cover 360 degrees or (2 x pi) radians.
-
Amplitude: Amplitude is represented by the y-axis of a plotted pressure wave. The strength at which the molecules pull or push away from each other, which will also depend upon the resistance offered by the medium, will determine how far above and below zero - the point of equilibrium - the wave fluctuates. The greater the y-value the greater the amplitude of our wave. The greater the compressions and rarefactions, the greater the amplitude.
Transduction
The analogue sound waves we hear in the world around us need to be converted into an electrical signal in order to be amplified or sent to a soundcard for recording. The process of converting acoustical energy in the form of pressure waves into an electrical signal is carried out by a device known as a a transducer.
A transducer, which is usually found in microphones, produces a changing electrical voltage that mirrors the changing compression and rarefaction of the air molecules caused by the sound wave. The continuous variation of pressure is therefore 'transduced' into continuous variation of voltage. The greater the variation of pressure the greater the variation of voltage that is sent to the computer.
Ideally the transduction process should be as transparent as possible: whatever goes in should come out as a perfect analogue in a voltage representation. In reality however this will not be the case, noise and distortion are always incorporated into the signal. Every time sound passes through a transducer or is transmitted electrically a change in signal quality will result. When we talk of 'noise' we are talking specifically about any unwanted signal captured during the transduction process. This normally manifests itself as an unwanted 'hiss'.
Sampling
The analogue voltage that corresponds to an acoustic signal changes continuously so that at each instant in time it will have a different value. It is not possible for a computer to receive the value of the voltage for every instant because of the physical limitations of both the computer and the data converters (remember also that there are an infinite number of instances between every two instances!).
What the soundcard can do, however, is to measure the power of the analogue voltage at intervals of equal duration. This is how all digital recording works and this is known as 'sampling'. The result of this sampling process is a discrete, or digital, signal which is no more than a sequence of numbers corresponding to the voltage at each successive moment of sampling.
Below left is a diagram showing a sinusoidal waveform. The vertical lines that run through the diagram represents the points in time when a snapshot is taken of the signal. After the sampling has taken place we are left with what is known as a discrete signal consisting of a collection of audio samples, as illustrated in the diagram on the right hand side below. If one is recording using a typical audio editor the incoming samples will be stored in the computer's RAM (Random Access Memory). In Csound one can process the incoming audio samples in real time and output a new stream of samples or write them to disk in the form of a sound file.
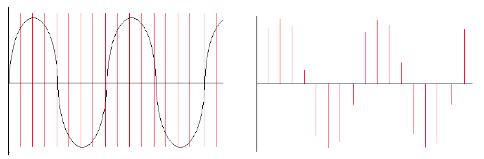
It is important to remember that each sample represents the amount of voltage, positive or negative, that was present in the signal at the point in time at which the sample or snapshot was taken.
The same principle applies to recording of live video: a video camera takes a sequence of pictures of motion and most video cameras will take between 30 and 60 still pictures a second. Each picture is called a frame and when these frames are played in sequence at a rate corresponding to that at which they were taken we no longer perceive them as individual pictures, we perceive them instead as a continuous moving image.
Analogue versus Digital
In general, analogue systems can be quite unreliable when it comes to noise and distortion. Each time something is copied or transmitted some noise and distortion is introduced into the process. If this is repeated many times, the cumulative effect can deteriorate a signal quite considerably. It is for this reason that the music industry has almost entirely turned to digital technology. One particular advantage of storing a signal digitally is that once the changing signal has been converted to a discrete series of values, it can effectively be 'cloned' an clones can be made of that clone with no loss or distortion of data. Mathematical routines can be applied to prevent errors in transmission, which could otherwise introduce noise into the signal.
Sample Rate and the Sampling Theorem
The sample rate describes the number of samples (pictures/snapshots) taken each second. To sample an audio signal correctly it is important to pay attention to the sampling theorem:
"To represent digitally a signal containing frequencies up to X Hz, it is necessary to use a sampling rate of at least 2X samples per second"
According to this theorem, a soundcard or any other digital recording device will not be able to represent any frequency above 1/2 the sampling rate. Half the sampling rate is also referred to as the Nyquist frequency, after the Swedish physicist Harry Nyquist who formalized the theory in the 1920s. What it all means is that any signal with frequencies above the Nyquist frequency will be misrepresented and will actually produce a frequency lower than the one being sampled. When this happens it results in what is known as 'aliasing' or 'foldover'.
Aliasing
Here is a graphical representation of aliasing.
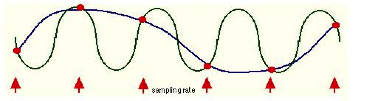
The sinusoidal waveform in blue is being sampled where arrows are indicated along the timeline. The line that joins the red circles together is the captured waveform. As you can see, the captured waveform and the original waveform express different frequencies.
Here is another example:

We can see that if the sample rate is 40,000 there is no problem with sampling a signal that is 10KHz. On the other hand, in the second example it can be seen that a 30kHz waveform is not going to be correctly sampled. In fact we end up with a waveform that is 10kHz, rather than 30kHz. This may seem like an academic proposition in that we will never be able to hear a 30KHz waveform anyway but some synthesis and DSP techniques procedures will produce these frequencies as unavoidable by-products and we need to ensure that they do not result in unwanted artifacts.
The following Csound instrument plays a 1000 Hz tone first directly, and then because the frequency is 1000 Hz lower than the sample rate of 44100 Hz:
EXAMPLE 01A01_Aliasing.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1
asig oscils .2, p4, 0
outs asig, asig
endin
</CsInstruments>
<CsScore>
i 1 0 2 1000 ;1000 Hz tone
i 1 3 2 43100 ;43100 Hz tone sounds like 1000 Hz because of aliasing
</CsScore>
</CsoundSynthesizer>
The same phenomenon takes places in film and video too. You may recall having seen wagon wheels apparently turn at the wrong speed in old Westerns. Let us say for example that a camera is taking 60 frames per second of a wheel moving. In one example, if the wheel is completing one rotation in exactly 1/60th of a second, then every picture looks the same and as a result the wheel appears to be motionless. If the wheel speeds up, i.e. it increases its rotational frequency, it will appear as if the wheel is slowly turning backwards. This is because the wheel will complete more than a full rotation between each snapshot.
As an aside, it is worth observing that a lot of modern 'glitch' music intentionally makes a feature of the spectral distortion that aliasing induces in digital audio. Csound is perfectly capable of imitating the effects of aliasing while being run at any sample rate - if that is what you desire.
Audio-CD Quality uses a sample rate of 44100Kz (44.1 kHz). This means that CD quality can only represent frequencies up to 22050Hz. Humans typically have an absolute upper limit of hearing of about 20Khz thus making 44.1KHz a reasonable standard sampling rate.
Bits, Bytes and Words. Understanding Binary.
All digital computers represent data as a collection of bits (short for binary digit). A bit is the smallest possible unit of information. One bit can only be in one of two states - off or on, 0 or 1. The meaning of the bit - which can represent almost anything - is unimportant at this point, the thing to remember is that all computer data - a text file on disk, a program in memory, a packet on a network - is ultimately a collection of bits.
Bits in groups of eight are called bytes, and one byte usually represents a single character of data in the computer. It's a little used term, but you might be interested in knowing that a nibble is half a byte (usually 4 bits).
The Binary System
All digital computers work in a environment that has only two variables, 0 and 1. All numbers in our decimal system therefore must be translated into 0's and 1's in the binary system. If you think of binary numbers in terms of switches. With one switch you can represent up to two different numbers.
0 (OFF) = Decimal 0
1 (ON) = Decimal 1
Thus, a single bit represents 2 numbers, two bits can represent 4 numbers, three bits represent 8 numbers, four bits represent 16 numbers, and so on up to a byte, or eight bits, which represents 256 numbers. Therefore each added bit doubles the amount of possible numbers that can be represented. Put simply, the more bits you have at your disposal the more information you can store.
Bit-depth Resolution
Apart from the sample rate, another important attribute that can affect the fidelity of a digital signal is the accuracy with which each sample is known, its resolution or granularity. Every sample obtained is set to a specific amplitude (the measure of strength for each voltage) level. Each voltage measurement will probably have to be rounded up or down to the nearest digital value available. The number of levels available depends on the precision of the measurement in bits, i.e. how many binary digits are used to store the samples. The number of bits that a system can use is normally referred to as the bit-depth resolution.
If the bit-depth resolution is 3 then there are 8 possible levels of amplitude that we can use for each sample. We can see this in the diagram below. At each sampling period the soundcard plots an amplitude. As we are only using a 3-bit system the resolution is not good enough to plot the correct amplitude of each sample. We can see in the diagram that some vertical lines stop above or below the real signal. This is because our bit-depth is not high enough to plot the amplitude levels with sufficient accuracy at each sampling period.
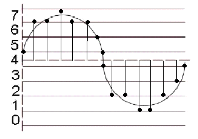
The standard resolution for CDs is 16 bit, which allows for 65536 different possible amplitude levels, 32767 either side of the zero axis. Using bit rates lower than 16 is not a good idea as it will result in noise being added to the signal. This is referred to as quantization noise and is a result of amplitude values being excessively rounded up or down when being digitized. Quantization noise becomes most apparent when trying to represent low amplitude (quiet) sounds. Frequently a tiny amount of noise, known as a dither signal, will be added to digital audio before conversion back into an analogue signal. Adding this dither signal will actually reduce the more noticeable noise created by quantization. As higher bit depth resolutions are employed in the digitizing process the need for dithering is reduced. A general rule is to use the highest bit rate available.
Many electronic musicians make use of deliberately low bit depth quantization in order to add noise to a signal. The effect is commonly known as 'bit-crunching' and is relatively easy to implement in Csound.
ADC / DAC
The entire process, as described above, of taking an analogue signal and converting it to a digital signal is referred to as analogue to digital conversion, or ADC. Of course digital to analogue conversion, DAC, is also possible. This is how we get to hear our music through our PC's headphones or speakers. For example, if one plays a sound from Media Player or iTunes the software will send a series of numbers to the computer soundcard. In fact it will most likely send 44100 numbers a second. If the audio that is playing is 16 bit then these numbers will range from -32768 to +32767.
When the sound card receives these numbers from the audio stream it will output corresponding voltages to a loudspeaker. When the voltages reach the loudspeaker they cause the loudspeaker's magnet to move inwards and outwards. This causes a disturbance in the air around the speaker - the compressions and rarefactions introduced at the beginning of this chapter - resulting in what we perceive as sound.
FREQUENCIES
As mentioned in the previous section, frequency is defined as the number of cycles or periods per second. Frequency is measured in Hertz. If a tone has a frequency of 440Hz it completes 440 cycles every second. Given a tone's frequency, one can easily calculate the period of any sound. Mathematically, the period is the reciprocal of the frequency and vice versa. In equation form, this is expressed as follows.
Frequency = 1/Period Period = 1/Frequency
Therefore the frequency is the inverse of the period, so a wave of 100Hz frequency has a period of 1/100 or 0.01 seconds, likewise a frequency of 256Hz has a period of 1/256, or 0.004 seconds. To calculate the wavelength of a sound in any given medium we can use the following equation:
λ = Velocity/Frequency
For instance, a wave of 1000 Hz in air (velocity of diffusion about 340 m/s) has a length of approximately 340/1000 m = 34 cm.
Upper and Lower Limits of Hearing
It is generally stated that the human ear can hear sounds in the range 20Hz to 20,000Hz (20kHz). This upper limit tends to decrease with age due to a condition known as presbyacusis, or age related hearing loss. Most adults can hear to about 16 kHz while most children can hear beyond this. At the lower end of the spectrum the human ear does not respond to frequencies below 20 Hz, with 40 of 50 Hz being the lowest most people can perceive.
So, in the following example, you will not hear the first (10 Hz) tone, and probably not the last (20 kHz) one, but hopefully the other ones (100 Hz, 1000 Hz, 10000 Hz):
EXAMPLE 01B01_LimitsOfHearing.csd
<CsoundSynthesizer>
<CsOptions>
-odac -m0
</CsOptions>
<CsInstruments>
;example by joachim heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1
prints "Playing %d Hertz!\n", p4
asig oscils .2, p4, 0
outs asig, asig
endin
</CsInstruments>
<CsScore>
i 1 0 2 10
i . + . 100
i . + . 1000
i . + . 10000
i . + . 20000
</CsScore>
</CsoundSynthesizer>
Logarithms, Frequency Ratios and Intervals
A lot of basic maths is about simplification of complex equations. Shortcuts are taken all the time to make things easier to read and equate. Multiplication can be seen as a shorthand for repeated additions, for example, 5x10 = 5+5+5+5+5+5+5+5+5+5. Exponents are shorthand for repeated multiplications, 35 = 3x3x3x3x3. Logarithms are shorthand for exponents and are used in many areas of science and engineering in which quantities vary over a large range. Examples of logarithmic scales include the decibel scale, the Richter scale for measuring earthquake magnitudes and the astronomical scale of stellar brightnesses. Musical frequencies also work on a logarithmic scale; more on this later.
Intervals in music describe the distance between two notes. When dealing with standard musical notation it is easy to determine an interval between two adjacent notes. For example a perfect 5th is always made up of 7 semitones. When dealing with Hz values things are different. A difference of say 100Hz does not always equate to the same musical interval. This is because musical intervals as we hear them are represented in Hz as frequency ratios. An octave for example is always 2:1. That is to say every time you double a Hz value you will jump up by a musical interval of an octave.
Consider the following. A flute can play the note A at 440Hz. If the player plays another A an octave above it at 880 Hz the difference in Hz is 440. Now consider the piccolo, the highest pitched instrument of the orchestra. It can play a frequency of 2000Hz but it can also play an octave above this at 4000Hz (2 x 2000Hz). While the difference in Hertz between the two notes on the flute is only 440Hz, the difference between the two high pitched notes on a piccolo is 1000Hz yet they are both only playing notes one octave apart.
What all this demonstrates is that the higher two pitches become, the greater the difference in Hertz required for us to recognize the spacing as the same musical interval. We can use simple ratios to represent a number of familiar intervals; for example the unison: (1:1), the octave: (2:1), the perfect fifth (3:2), the perfect fourth (4:3), the major third (5:4) and the minor third (6:5); but it should be noted that most of these intervals are only represented with absolute precision when using just intonation. In equal temperament, the dominant method used in the tuning of many instruments, only unison and the octave are represented with these precise ratios.
The following example shows the difference between adding a certain frequency and applying a ratio. First, the frequencies of 100, 400 and 800 Hz all get an addition of 100 Hz. This sounds very different, though the added frequency is the same. Second, the ratio 3/2 (perfect fifth) is applied to the same frequencies. This spacing sounds constant, although the frequency displacement is different each time.
EXAMPLE 01B02_Adding_vs_ratio.csd
<CsoundSynthesizer>
<CsOptions>
--env:SSDIR+=../SourceMaterials -odac -m0
</CsOptions>
<CsInstruments>
;example by joachim heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1
prints "Playing %d Hertz!\n", p4
asig oscils .2, p4, 0
outs asig, asig
endin
instr 2
prints "Adding %d Hertz to %d Hertz!\n", p5, p4
asig oscils .2, p4+p5, 0
outs asig, asig
endin
instr 3
prints "Applying the ratio of %f (adding %d Hertz) to %d Hertz!\n", p5, p4*p5, p4
asig oscils .2, p4*p5, 0
outs asig, asig
endin
</CsInstruments>
<CsScore>
;adding a certain frequency (instr 2)
i 1 0 1 100
i 2 1 1 100 100
i 1 3 1 400
i 2 4 1 400 100
i 1 6 1 800
i 2 7 1 800 100
;applying a certain ratio (instr 3)
i 1 10 1 100
i 3 11 1 100 [3/2]
i 1 13 1 400
i 3 14 1 400 [3/2]
i 1 16 1 800
i 3 17 1 800 [3/2]
</CsScore>
</CsoundSynthesizer>
So what of the algorithms mentioned above. As some readers will know the current preferred method of tuning western instruments is based on equal temperament. Essentially this means that all octaves are split into 12 equal intervals. Therefore a semitone has a ratio of 2(1/12), which is approximately 1.059463.
So what about the reference to logarithms in the heading above? As stated previously, logarithms are shorthand for exponents. 2(1/12)= 1.059463 can also be written as log2(1.059463)= 1/12. Therefore musical frequency works on a logarithmic scale.
MIDI Notes
Csound can easily deal with MIDI notes and comes with functions that will convert MIDI notes to Hertz values and back again. In MIDI speak A440 is equal to A4 and is MIDI note 69. You can think of A4 as being the fourth A from the lowest A we can hear; well, almost hear.
Caution: like many 'standards' there is occasional disagreement about the mapping between frequency and octave number. You may occasionally encounter A440 being described as A3.
INTENSITIES
Real World Intensities and Amplitudes
There are many ways to describe a sound physically. One of the most common is the sound intensity level (SIL). It describes the amount of power on a certain surface, so its unit is Watts per square meter (). The range of human hearing is about
at the threshold of hearing to
at the threshold of pain. For ordering this immense range, and to facilitate the measurement of one sound intensity based upon its ratio with another, a logarithmic scale is used. The unit Bel describes the relation of one intensity I to a reference intensity I0 as follows:
Sound Intensity Level in Bel
If, for example, the ratio is 10, this is 1 Bel. If the ratio is 100, this is 2 Bel.
For real world sounds, it makes sense to set the reference value to the threshold of hearing which has been fixed as
at 1000 Hertz. So the range of human hearing covers about 12 Bel. Usually 1 Bel is divided into 10 decibel, so the common formula for measuring a sound intensity is:
sound intensity level (SIL) in decibel (dB) with
While the sound intensity level is useful in describing the way in which human hearing works, the measurement of sound is more closely related to the sound pressure deviations. Sound waves compress and expand the air particles and by this they increase and decrease the localized air pressure. These deviations are measured and transformed by a microphone. The question arises: what is the relationship between the sound pressure deviations and the sound intensity? The answer is: sound intensity changes are proportional to the square of the sound pressure changes
. As a formula:
Relation between Sound Intensity and Sound Pressure
Let us take an example to see what this means. The sound pressure at the threshold of hearing can be fixed at . This value is the reference value of the Sound Pressure Level (SPL). If we now have a value of
, the corresponding sound intensity relationship can be calculated as:
Therefore a factor of 10 in a pressure relationship yields a factor of 100 in the intensity relationship. In general, the dB scale for the pressure P related to the pressure P0 is:
Sound pressure level (SPL) in decibels (dB) with
Working with digital audio means working with amplitudes. Any audio file is a sequence of amplitudes. What you generate in Csound and write either to the DAC in realtime or to a sound file, are again nothing but a sequence of amplitudes. As amplitudes are directly related to the sound pressure deviations, all the relationships between sound intensity and sound pressure can be transferred to relationships between sound intensity and amplitudes:
Relationship between intensity and amplitudes
Decibel (dB) scale of amplitudes with any amplitude
related to another amplitude
If you drive an oscillator with an amplitude of 1, and another oscillator with an amplitude of 0.5 and you want to know the difference in dB, you can calculate this as follows:
The most useful thing to bear in mind is that when you double an amplitude this will provide a change of +6 dB, or when you have halve an amplitude this will provide a change in of -6 dB.
What is 0 dB?
As described in the last section, any dB scale - for intensities, pressures or amplitudes - is just a way to describe a relationship. To have any sort of quantitative measurement you will need to know the reference value referred to as "0 dB". For real world sounds, it makes sense to set this level to the threshold of hearing. This is done, as we saw, by setting the SIL to and the SPL to
.
When working with digital sound within a computer, this method for defining 0dB will not make any sense. The loudness of the sound produced in the computer will ultimately depend on the amplification and the speakers, and the amplitude level set in your audio editor or in Csound will only apply an additional, and not an absolute, sound level control. Nevertheless, there is a rational reference level for the amplitudes. In a digital system, there is a strict limit for the maximum number you can store as amplitude. This maximum possible level is normally used as the reference point for 0 dB.
Each program connects this maximum possible amplitude with a number. Usually it is '1' which is a good choice, because you know that everything above 1 is clipping, and you have a handy relation for lower values. But actually this value is nothing but a setting, and in Csound you are free to set it to any value you like via the 0dbfs opcode. Usually you should use this statement in the orchestra header:
0dbfs = 1
This means: "Set the level for zero dB as full scale to 1 as reference value." Note that for historical reasons the default value in Csound is not 1 but 32768. So you must have this 0dbfs=1 statement in your header if you want to use the amplitude convention used by most modern audio programming environments.
dB Scale Versus Linear Amplitude
Now we will consider some practical consequences of what we have discussed so far. One major point is that for achieving perceivably smooth changes across intensity levels you must not use a simple linear transition of the amplitudes, but a linear transition of the dB equivalent. The following example shows a linear rise of the amplitudes from 0 to 1, and then a linear rise of the dB's from -80 to 0 dB, both over 10 seconds.
EXAMPLE 01C01_db_vs_linear.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;example by joachim heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1 ;linear amplitude rise
kamp line 0, p3, 1 ;amp rise 0->1
asig oscils 1, 1000, 0 ;1000 Hz sine
aout = asig * kamp
outs aout, aout
endin
instr 2 ;linear rise of dB
kdb line -80, p3, 0 ;dB rise -80 -> 0
asig oscils 1, 1000, 0 ;1000 Hz sine
kamp = ampdb(kdb) ;transformation db -> amp
aout = asig * kamp
outs aout, aout
endin
</CsInstruments>
<CsScore>
i 1 0 10
i 2 11 10
</CsScore>
</CsoundSynthesizer>
The first note, which employs a linear rise in amplitude, is perceived as rising quickly in intensity with the rate of increase slowing quickly. The second note, which employs a linear rise in decibels, is perceived as a more constant rise in intensity.
RMS Measurement
Sound intensity depends on many factors. One of the most important is the effective mean of the amplitudes in a certain time span. This is called the Root Mean Square (RMS) value. To calculate it, you have (1) to calculate the squared amplitudes of number N samples. Then you (2) divide the result by N to calculate the mean of it. Finally (3) take the square root.
Let us consider a simple example and then look how to derive rms values within Csound. Assuming we have a sine wave which consists of 16 samples, we get these amplitudes:
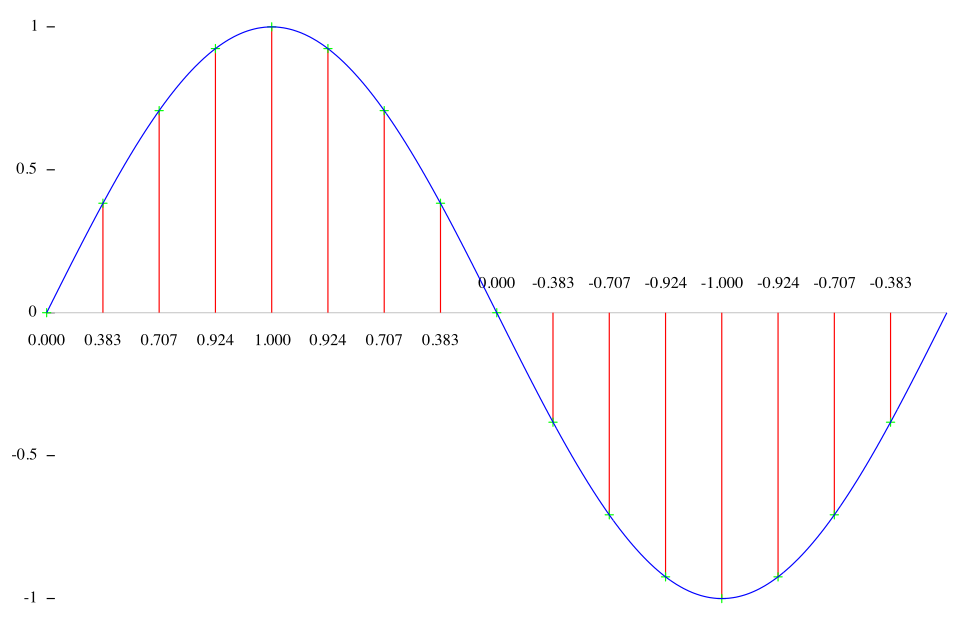
These are the squared amplitudes:
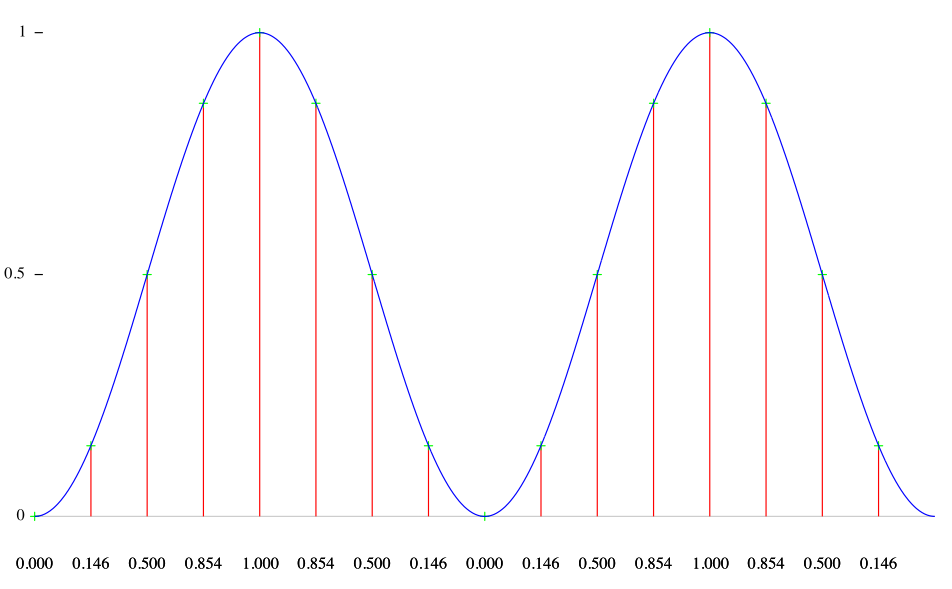
The mean of these values is:
(0+0.146+0.5+0.854+1+0.854+0.5+0.146+0+0.146+0.5+0.854+1+0.854+0.5+0.146)/16=8/16=0.5
And the resulting RMS value is sqrt(0.5) = 0.707 .
The rms opcode in Csound calculates the RMS power in a certain time span, and smoothes the values in time according to the ihp parameter: the higher this value is (the default is 10 Hz), the quicker this measurement will respond to changes, and vice versa. This opcode can be used to implement a self-regulating system, in which the rms opcode prevents the system from exploding. Each time the rms value exceeds a certain value, the amount of feedback is reduced. This is an example1 :
EXAMPLE 01C02_rms_feedback_system.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;example by Martin Neukom, adapted by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1 ;table with a sine wave
instr 1
a3 init 0
kamp linseg 0, 1.5, 0.2, 1.5, 0 ;envelope for initial input
asnd poscil kamp, 440, giSine ;initial input
if p4 == 1 then ;choose between two sines ...
adel1 poscil 0.0523, 0.023, giSine
adel2 poscil 0.073, 0.023, giSine,.5
else ;or a random movement for the delay lines
adel1 randi 0.05, 0.1, 2
adel2 randi 0.08, 0.2, 2
endif
a0 delayr 1 ;delay line of 1 second
a1 deltapi adel1 + 0.1 ;first reading
a2 deltapi adel2 + 0.1 ;second reading
krms rms a3 ;rms measurement
delayw asnd + exp(-krms) * a3 ;feedback depending on rms
a3 reson -(a1+a2), 3000, 7000, 2 ;calculate a3
aout linen a1/3, 1, p3, 1 ;apply fade in and fade out
outs aout, aout
endin
</CsInstruments>
<CsScore>
i 1 0 60 1 ;two sine movements of delay with feedback
i 1 61 . 2 ;two random movements of delay with feedback
</CsScore>
</CsoundSynthesizer>
Fletcher-Munson Curves
The range of human hearing is roughly from 20 to 20000 Hz, but within this range, the hearing is not equally sensitive to intensity. The most sensitive region is around 3000 Hz. If a sound is operating in the upper or lower limits of this range, it will need greater intensity in order to be perceived as equally loud.
These curves of equal loudness are mostly called "Fletcher-Munson Curves" because of the paper of H. Fletcher and W. A. Munson in 1933. They look like this:
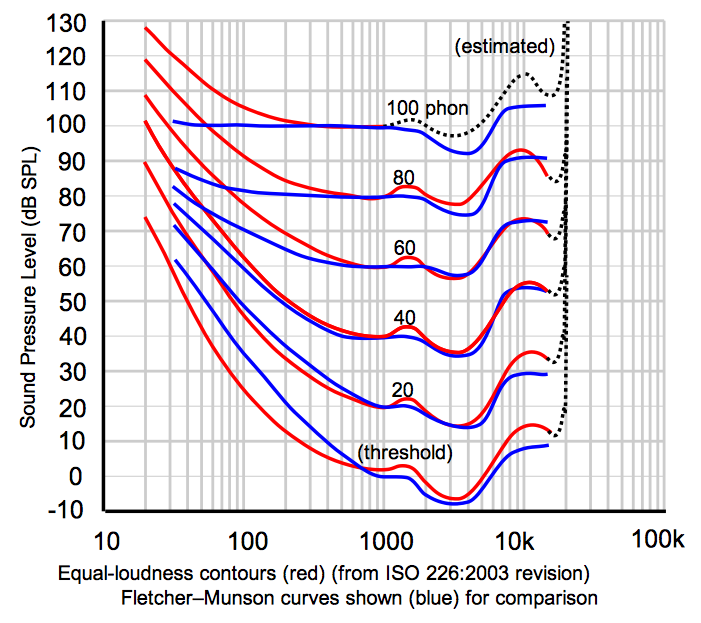
Try the following test. During the first 5 seconds you will hear a tone of 3000 Hz. Adjust the level of your amplifier to the lowest possible level at which you still can hear the tone. Next you hear a tone whose frequency starts at 20 Hertz and ends at 20000 Hertz, over 20 seconds. Try to move the fader or knob of your amplification exactly in a way that you still can hear anything, but as soft as possible. The movement of your fader should roughly be similar to the lowest Fletcher-Munson-Curve: starting relatively high, going down and down until 3000 Hertz, and then up again. Of course, this effectiveness of this test will also depend upon the quality of your speaker hardware. If your speakers do not provide adequate low frequency response, you will not hear anything in the bass region.
EXAMPLE 01C03_FletcherMunson.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1 ;table with a sine wave
instr 1
kfreq expseg p4, p3, p5
printk 1, kfreq ;prints the frequencies once a second
asin poscil .2, kfreq, giSine
aout linen asin, .01, p3, .01
outs aout, aout
endin
</CsInstruments>
<CsScore>
i 1 0 5 1000 1000
i 1 6 20 20 20000
</CsScore>
</CsoundSynthesizer>
It is very important to bear in mind when designing instruments that the perceived loudness of a sound will depend upon its frequency content. You must remain aware that projecting a 30 Hz sine at a certain amplitude will be perceived differently to a 3000 Hz sine at the same amplitude; the latter will sound much louder.
- cf Martin Neukom, Signale Systeme Klangsynthese, Zürich 2003, p. 383^
RANDOM
This chapter is in three parts. Part I provides a general introduction to the concepts behind random numbers and how to work with them in Csound. Part II focusses on a more mathematical approach. Part III introduces a number of opcodes for generating random numbers, functions and distributions and demonstrates their use in musical examples.
I. GENERAL INTRODUCTION
Random is Different
The term random derives from the idea of a horse that is running so fast it becomes 'out of control' or 'beyond predictability'.1 Yet there are different ways in which to run fast and to be out of control; therefore there are different types of randomness.
We can divide types of randomness into two classes. The first contains random events that are independent of previous events. The most common example for this is throwing a die. Even if you have just thrown three '1's in a row, when thrown again, a '1' has the same probability as before (and as any other number). The second class of random number involves random events which depend in some way upon previous numbers or states. Examples here are Markov chains and random walks.
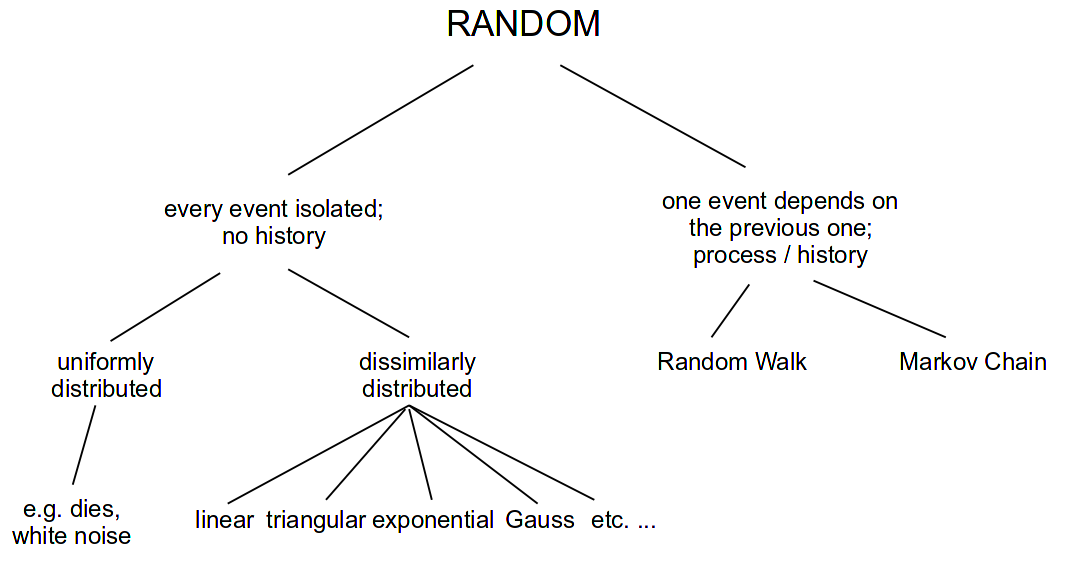
The use of randomness in electronic music is widespread. In this chapter, we shall try to explain how the different random horses are moving, and how you can create and modify them on your own. Moreover, there are many pre-built random opcodes in Csound which can be used out of the box (see the overview in the Csound Manual). The final section of this chapter introduces some musically interesting applications of them.
Random Without History
A computer is typically only capable of computation. Computations are deterministic processes: one input will always generate the same output, but a random event is not predictable. To generate something which looks like a random event, the computer uses a pseudo-random generator.
The pseudo-random generator takes one number as input, and generates another number as output. This output is then the input for the next generation. For a huge amount of numbers, they look as if they are randomly distributed, although everything depends on the first input: the seed. For one given seed, the next values can be predicted.
Uniform Distribution
The output of a classical pseudo-random generator is uniformly distributed: each value in a given range has the same likelihood of occurence. The first example shows the influence of a fixed seed (using the same chain of numbers and beginning from the same location in the chain each time) in contrast to a seed being taken from the system clock (the usual way of imitating unpredictability). The first three groups of four notes will always be the same because of the use of the same seed whereas the last three groups should always have a different pitch.
EXAMPLE 01D01_different_seed.csd
<CsoundSynthesizer>
<CsOptions>
-d -odac -m0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr generate
;get seed: 0 = seeding from system clock
; otherwise = fixed seed
seed p4
;generate four notes to be played from subinstrument
iNoteCount = 0
until iNoteCount == 4 do
iFreq random 400, 800
event_i "i", "play", iNoteCount, 2, iFreq
iNoteCount += 1 ;increase note count
enduntil
endin
instr play
iFreq = p4
print iFreq
aImp mpulse .5, p3
aMode mode aImp, iFreq, 1000
aEnv linen aMode, 0.01, p3, p3-0.01
outs aEnv, aEnv
endin
</CsInstruments>
<CsScore>
;repeat three times with fixed seed
r 3
i "generate" 0 2 1
;repeat three times with seed from the system clock
r 3
i "generate" 0 1 0
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Note that a pseudo-random generator will repeat its series of numbers after as many steps as are given by the size of the generator. If a 16-bit number is generated, the series will be repeated after 65536 steps. If you listen carefully to the following example, you will hear a repetition in the structure of the white noise (which is the result of uniformly distributed amplitudes) after about 1.5 seconds in the first note.2 In the second note, there is no perceivable repetition as the random generator now works with a 31-bit number.
EXAMPLE 01D02_white_noises.csd
<CsoundSynthesizer>
<CsOptions>
-d -odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr white_noise
iBit = p4 ;0 = 16 bit, 1 = 31 bit
;input of rand: amplitude, fixed seed (0.5), bit size
aNoise rand .1, 0.5, iBit
outs aNoise, aNoise
endin
</CsInstruments>
<CsScore>
i "white_noise" 0 10 0
i "white_noise" 11 10 1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Two more general notes about this:
- The way to set the seed differs from opcode to opcode. There are several opcodes such as rand featured above, which offer the choice of setting a seed as input parameter. For others, such as the frequently used random family, the seed can only be set globally via the seed statement. This is usually done in the header so a typical statement would be:
<CsInstruments> sr = 44100 ksmps = 32 nchnls = 2 0dbfs = 1 seed = 0 ;seeding from current time
...
- Random number generation in Csound can be done at any rate. The type of the output variable tells you whether you are generating random values at i-, k- or a-rate. Many random opcodes can work at all these rates, for instance random:
1) ires random imin, imax 2) kres random kmin, kmax 3) ares random kmin, kmax
In the first case, a random value is generated only once, when an instrument is called, at initialisation. The generated value is then stored in the variable ires. In the second case, a random value is generated at each k-cycle, and stored in kres. In the third case, in each k-cycle as many random values are stored as the audio vector has in size, and stored in the variable ares. Have a look at example 03A16_Random_at_ika.csd to see this at work. Chapter 03A tries to explain the background of the different rates in depth, and how to work with them.
Other Distributions
The uniform distribution is the one each computer can output via its pseudo-random generator. But there are many situations you will not want a uniformly distributed random, but any other shape. Some of these shapes are quite common, but you can actually build your own shapes quite easily in Csound. The next examples demonstrate how to do this. They are based on the chapter in Dodge/Jerse3 which also served as a model for many random number generator opcodes in Csound.4
Linear
A linear distribution means that either lower or higher values in a given range are more likely:
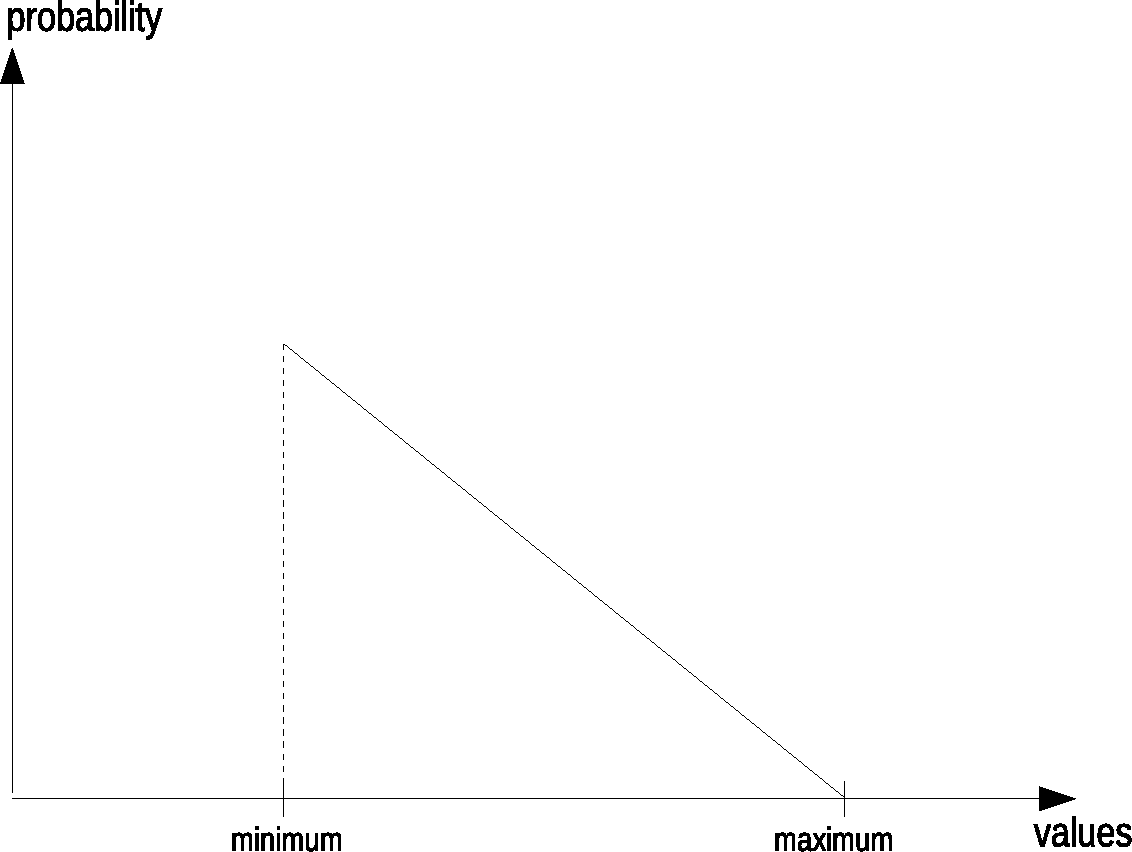
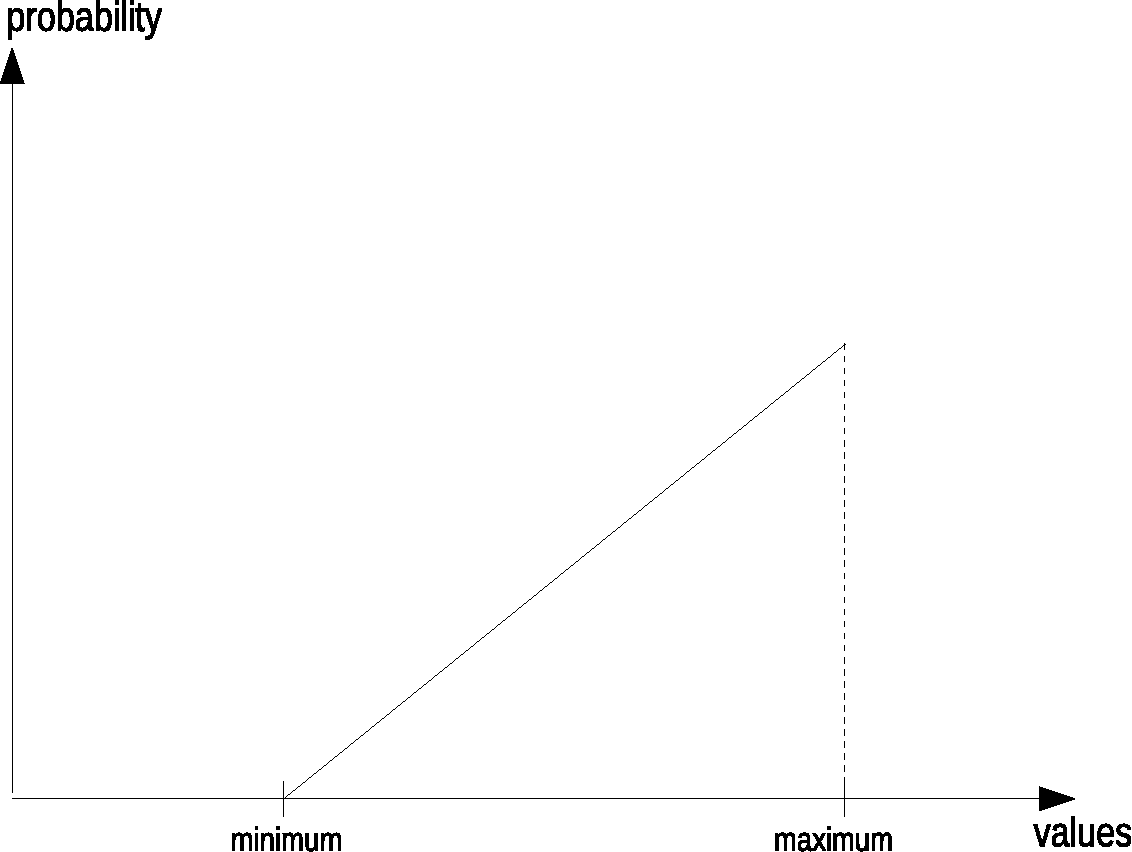
To get this behaviour, two uniform random numbers are generated, and the lower is taken for the first shape. If the second shape with the precedence of higher values is needed, the higher one of the two generated numbers is taken. The next example implements these random generators as User Defined Opcodes. First we hear a uniform distribution, then a linear distribution with precedence of lower pitches (but longer durations), at least a linear distribution with precedence of higher pitches (but shorter durations).
EXAMPLE 01D03_linrand.csd
<CsoundSynthesizer>
<CsOptions>
-d -odac -m0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0
;****DEFINE OPCODES FOR LINEAR DISTRIBUTION****
opcode linrnd_low, i, ii
;linear random with precedence of lower values
iMin, iMax xin
;generate two random values with the random opcode
iOne random iMin, iMax
iTwo random iMin, iMax
;compare and get the lower one
iRnd = iOne < iTwo ? iOne : iTwo
xout iRnd
endop
opcode linrnd_high, i, ii
;linear random with precedence of higher values
iMin, iMax xin
;generate two random values with the random opcode
iOne random iMin, iMax
iTwo random iMin, iMax
;compare and get the higher one
iRnd = iOne > iTwo ? iOne : iTwo
xout iRnd
endop
;****INSTRUMENTS FOR THE DIFFERENT DISTRIBUTIONS****
instr notes_uniform
prints "... instr notes_uniform playing:\n"
prints "EQUAL LIKELINESS OF ALL PITCHES AND DURATIONS\n"
;how many notes to be played
iHowMany = p4
;trigger as many instances of instr play as needed
iThisNote = 0
iStart = 0
until iThisNote == iHowMany do
iMidiPch random 36, 84 ;midi note
iDur random .5, 1 ;duration
event_i "i", "play", iStart, iDur, int(iMidiPch)
iStart += iDur ;increase start
iThisNote += 1 ;increase counter
enduntil
;reset the duration of this instr to make all events happen
p3 = iStart + 2
;trigger next instrument two seconds after the last note
event_i "i", "notes_linrnd_low", p3, 1, iHowMany
endin
instr notes_linrnd_low
prints "... instr notes_linrnd_low playing:\n"
prints "LOWER NOTES AND LONGER DURATIONS PREFERRED\n"
iHowMany = p4
iThisNote = 0
iStart = 0
until iThisNote == iHowMany do
iMidiPch linrnd_low 36, 84 ;lower pitches preferred
iDur linrnd_high .5, 1 ;longer durations preferred
event_i "i", "play", iStart, iDur, int(iMidiPch)
iStart += iDur
iThisNote += 1
enduntil
;reset the duration of this instr to make all events happen
p3 = iStart + 2
;trigger next instrument two seconds after the last note
event_i "i", "notes_linrnd_high", p3, 1, iHowMany
endin
instr notes_linrnd_high
prints "... instr notes_linrnd_high playing:\n"
prints "HIGHER NOTES AND SHORTER DURATIONS PREFERRED\n"
iHowMany = p4
iThisNote = 0
iStart = 0
until iThisNote == iHowMany do
iMidiPch linrnd_high 36, 84 ;higher pitches preferred
iDur linrnd_low .3, 1.2 ;shorter durations preferred
event_i "i", "play", iStart, iDur, int(iMidiPch)
iStart += iDur
iThisNote += 1
enduntil
;reset the duration of this instr to make all events happen
p3 = iStart + 2
;call instr to exit csound
event_i "i", "exit", p3+1, 1
endin
;****INSTRUMENTS TO PLAY THE SOUNDS AND TO EXIT CSOUND****
instr play
;increase duration in random range
iDur random p3, p3*1.5
p3 = iDur
;get midi note and convert to frequency
iMidiNote = p4
iFreq cpsmidinn iMidiNote
;generate note with karplus-strong algorithm
aPluck pluck .2, iFreq, iFreq, 0, 1
aPluck linen aPluck, 0, p3, p3
;filter
aFilter mode aPluck, iFreq, .1
;mix aPluck and aFilter according to MidiNote
;(high notes will be filtered more)
aMix ntrpol aPluck, aFilter, iMidiNote, 36, 84
;panning also according to MidiNote
;(low = left, high = right)
iPan = (iMidiNote-36) / 48
aL, aR pan2 aMix, iPan
outs aL, aR
endin
instr exit
exitnow
endin
</CsInstruments>
<CsScore>
i "notes_uniform" 0 1 23 ;set number of notes per instr here
;instruments linrnd_low and linrnd_high are triggered automatically
e 99999 ;make possible to perform long (exit will be automatically)
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Triangular
In a triangular distribution the values in the middle of the given range are more likely than those at the borders. The probability transition between the middle and the extrema are linear:

The algorithm for getting this distribution is very simple as well. Generate two uniform random numbers and take the mean of them. The next example shows the difference between uniform and triangular distribution in the same environment as the previous example.
EXAMPLE 01D04_trirand.csd
<CsoundSynthesizer>
<CsOptions>
-d -odac -m0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0
;****UDO FOR TRIANGULAR DISTRIBUTION****
opcode trirnd, i, ii
iMin, iMax xin
;generate two random values with the random opcode
iOne random iMin, iMax
iTwo random iMin, iMax
;get the mean and output
iRnd = (iOne+iTwo) / 2
xout iRnd
endop
;****INSTRUMENTS FOR UNIFORM AND TRIANGULAR DISTRIBUTION****
instr notes_uniform
prints "... instr notes_uniform playing:\n"
prints "EQUAL LIKELINESS OF ALL PITCHES AND DURATIONS\n"
;how many notes to be played
iHowMany = p4
;trigger as many instances of instr play as needed
iThisNote = 0
iStart = 0
until iThisNote == iHowMany do
iMidiPch random 36, 84 ;midi note
iDur random .25, 1.75 ;duration
event_i "i", "play", iStart, iDur, int(iMidiPch)
iStart += iDur ;increase start
iThisNote += 1 ;increase counter
enduntil
;reset the duration of this instr to make all events happen
p3 = iStart + 2
;trigger next instrument two seconds after the last note
event_i "i", "notes_trirnd", p3, 1, iHowMany
endin
instr notes_trirnd
prints "... instr notes_trirnd playing:\n"
prints "MEDIUM NOTES AND DURATIONS PREFERRED\n"
iHowMany = p4
iThisNote = 0
iStart = 0
until iThisNote == iHowMany do
iMidiPch trirnd 36, 84 ;medium pitches preferred
iDur trirnd .25, 1.75 ;medium durations preferred
event_i "i", "play", iStart, iDur, int(iMidiPch)
iStart += iDur
iThisNote += 1
enduntil
;reset the duration of this instr to make all events happen
p3 = iStart + 2
;call instr to exit csound
event_i "i", "exit", p3+1, 1
endin
;****INSTRUMENTS TO PLAY THE SOUNDS AND EXIT CSOUND****
instr play
;increase duration in random range
iDur random p3, p3*1.5
p3 = iDur
;get midi note and convert to frequency
iMidiNote = p4
iFreq cpsmidinn iMidiNote
;generate note with karplus-strong algorithm
aPluck pluck .2, iFreq, iFreq, 0, 1
aPluck linen aPluck, 0, p3, p3
;filter
aFilter mode aPluck, iFreq, .1
;mix aPluck and aFilter according to MidiNote
;(high notes will be filtered more)
aMix ntrpol aPluck, aFilter, iMidiNote, 36, 84
;panning also according to MidiNote
;(low = left, high = right)
iPan = (iMidiNote-36) / 48
aL, aR pan2 aMix, iPan
outs aL, aR
endin
instr exit
exitnow
endin
</CsInstruments>
<CsScore>
i "notes_uniform" 0 1 23 ;set number of notes per instr here
;instr trirnd will be triggered automatically
e 99999 ;make possible to perform long (exit will be automatically)
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
More Linear and Triangular
Having written this with some very simple UDOs, it is easy to emphasise the probability peaks of the distributions by generating more than two random numbers. If you generate three numbers and choose the smallest of them, you will get many more numbers near the minimum in total for the linear distribution. If you generate three random numbers and take the mean of them, you will end up with more numbers near the middle in total for the triangular distribution.
If we want to write UDOs with a flexible number of sub-generated numbers, we have to write the code in a slightly different way. Instead of having one line of code for each random generator, we will use a loop, which calls the generator as many times as we wish to have units. A variable will store the results of the accumulation. Re-writing the above code for the UDO trirnd would lead to this formulation:
opcode trirnd, i, ii
iMin, iMax xin
;set a counter and a maximum count
iCount = 0
iMaxCount = 2
;set the accumulator to zero as initial value
iAccum = 0
;perform loop and accumulate
until iCount == iMaxCount do
iUniRnd random iMin, iMax
iAccum += iUniRnd
iCount += 1
enduntil
;get the mean and output
iRnd = iAccum / 2
xout iRnd
endop
To get this completely flexible, you only have to get iMaxCount as input argument. The code for the linear distribution UDOs is quite similar. -- The next example shows these steps:
- Uniform distribution.
- Linear distribution with the precedence of lower pitches and longer durations, generated with two units.
- The same but with four units.
- Linear distribution with the precedence of higher pitches and shorter durations, generated with two units.
- The same but with four units.
- Triangular distribution with the precedence of both medium pitches and durations, generated with two units.
- The same but with six units.
Rather than using different instruments for the different distributions, the next example combines all possibilities in one single instrument. Inside the loop which generates as many notes as desired by the iHowMany argument, an if-branch calculates the pitch and duration of one note depending on the distribution type and the number of sub-units used. The whole sequence (which type first, which next, etc) is stored in the global array giSequence. Each instance of instrument "notes" increases the pointer giSeqIndx, so that for the next run the next element in the array is being read. If the pointer has reached the end of the array, the instrument which exits Csound is called instead of a new instance of "notes".
EXAMPLE 01D05_more_lin_tri_units.csd
<CsoundSynthesizer>
<CsOptions>
-d -odac -m0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0
;****SEQUENCE OF UNITS AS ARRAY****/
giSequence[] array 0, 1.2, 1.4, 2.2, 2.4, 3.2, 3.6
giSeqIndx = 0 ;startindex
;****UDO DEFINITIONS****
opcode linrnd_low, i, iii
;linear random with precedence of lower values
iMin, iMax, iMaxCount xin
;set counter and initial (absurd) result
iCount = 0
iRnd = iMax
;loop and reset iRnd
until iCount == iMaxCount do
iUniRnd random iMin, iMax
iRnd = iUniRnd < iRnd ? iUniRnd : iRnd
iCount += 1
enduntil
xout iRnd
endop
opcode linrnd_high, i, iii
;linear random with precedence of higher values
iMin, iMax, iMaxCount xin
;set counter and initial (absurd) result
iCount = 0
iRnd = iMin
;loop and reset iRnd
until iCount == iMaxCount do
iUniRnd random iMin, iMax
iRnd = iUniRnd > iRnd ? iUniRnd : iRnd
iCount += 1
enduntil
xout iRnd
endop
opcode trirnd, i, iii
iMin, iMax, iMaxCount xin
;set a counter and accumulator
iCount = 0
iAccum = 0
;perform loop and accumulate
until iCount == iMaxCount do
iUniRnd random iMin, iMax
iAccum += iUniRnd
iCount += 1
enduntil
;get the mean and output
iRnd = iAccum / iMaxCount
xout iRnd
endop
;****ONE INSTRUMENT TO PERFORM ALL DISTRIBUTIONS****
;0 = uniform, 1 = linrnd_low, 2 = linrnd_high, 3 = trirnd
;the fractional part denotes the number of units, e.g.
;3.4 = triangular distribution with four sub-units
instr notes
;how many notes to be played
iHowMany = p4
;by which distribution with how many units
iWhich = giSequence[giSeqIndx]
iDistrib = int(iWhich)
iUnits = round(frac(iWhich) * 10)
;set min and max duration
iMinDur = .1
iMaxDur = 2
;set min and max pitch
iMinPch = 36
iMaxPch = 84
;trigger as many instances of instr play as needed
iThisNote = 0
iStart = 0
iPrint = 1
;for each note to be played
until iThisNote == iHowMany do
;calculate iMidiPch and iDur depending on type
if iDistrib == 0 then
printf_i "%s", iPrint, "... uniform distribution:\n"
printf_i "%s", iPrint, "EQUAL LIKELIHOOD OF ALL PITCHES AND DURATIONS\n"
iMidiPch random iMinPch, iMaxPch ;midi note
iDur random iMinDur, iMaxDur ;duration
elseif iDistrib == 1 then
printf_i "... linear low distribution with %d units:\n", iPrint, iUnits
printf_i "%s", iPrint, "LOWER NOTES AND LONGER DURATIONS PREFERRED\n"
iMidiPch linrnd_low iMinPch, iMaxPch, iUnits
iDur linrnd_high iMinDur, iMaxDur, iUnits
elseif iDistrib == 2 then
printf_i "... linear high distribution with %d units:\n", iPrint, iUnits
printf_i "%s", iPrint, "HIGHER NOTES AND SHORTER DURATIONS PREFERRED\n"
iMidiPch linrnd_high iMinPch, iMaxPch, iUnits
iDur linrnd_low iMinDur, iMaxDur, iUnits
else
printf_i "... triangular distribution with %d units:\n", iPrint, iUnits
printf_i "%s", iPrint, "MEDIUM NOTES AND DURATIONS PREFERRED\n"
iMidiPch trirnd iMinPch, iMaxPch, iUnits
iDur trirnd iMinDur, iMaxDur, iUnits
endif
;call subinstrument to play note
event_i "i", "play", iStart, iDur, int(iMidiPch)
;increase start tim and counter
iStart += iDur
iThisNote += 1
;avoid continuous printing
iPrint = 0
enduntil
;reset the duration of this instr to make all events happen
p3 = iStart + 2
;increase index for sequence
giSeqIndx += 1
;call instr again if sequence has not been ended
if giSeqIndx < lenarray(giSequence) then
event_i "i", "notes", p3, 1, iHowMany
;or exit
else
event_i "i", "exit", p3, 1
endif
endin
;****INSTRUMENTS TO PLAY THE SOUNDS AND EXIT CSOUND****
instr play
;increase duration in random range
iDur random p3, p3*1.5
p3 = iDur
;get midi note and convert to frequency
iMidiNote = p4
iFreq cpsmidinn iMidiNote
;generate note with karplus-strong algorithm
aPluck pluck .2, iFreq, iFreq, 0, 1
aPluck linen aPluck, 0, p3, p3
;filter
aFilter mode aPluck, iFreq, .1
;mix aPluck and aFilter according to MidiNote
;(high notes will be filtered more)
aMix ntrpol aPluck, aFilter, iMidiNote, 36, 84
;panning also according to MidiNote
;(low = left, high = right)
iPan = (iMidiNote-36) / 48
aL, aR pan2 aMix, iPan
outs aL, aR
endin
instr exit
exitnow
endin
</CsInstruments>
<CsScore>
i "notes" 0 1 23 ;set number of notes per instr here
e 99999 ;make possible to perform long (exit will be automatically)
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
With this method we can build probability distributions which are very similar to exponential or gaussian distributions.5 Their shape can easily be formed by the number of sub-units used.
Scalings
Random is a complex and sensible context. There are so many ways to let the horse go, run, or dance -- the conditions you set for this 'way of moving' are much more important than the fact that one single move is not predictable. What are the conditions of this randomness?
- Which Way. This is what has already been described: random with or without history, which probability distribution, etc.
- Which Range. This is a decision which comes from the composer/programmer. In the example above I have chosen pitches from Midi Note 36 to 84 (C2 to C6), and durations between 0.1 and 2 seconds. Imagine how it would have been sounded with pitches from 60 to 67, and durations from 0.9 to 1.1 seconds, or from 0.1 to 0.2 seconds. There is no range which is 'correct', everything depends on the musical idea.
- Which Development. Usually the boundaries will change in the run of a piece. The pitch range may move from low to high, or from narrow to wide; the durations may become shorter, etc.
- Which Scalings. Let us think about this more in detail.
In the example above we used two implicit scalings. The pitches have been scaled to the keys of a piano or keyboard. Why? We do not play piano here obviously ... -- What other possibilities might have been instead? One would be: no scaling at all. This is the easiest way to go -- whether it is really the best, or simple laziness, can only be decided by the composer or the listener.
Instead of using the equal tempered chromatic scale, or no scale at all, you can use any other ways of selecting or quantising pitches. Be it any which has been, or is still, used in any part of the world, or be it your own invention, by whatever fantasy or invention or system.
As regards the durations, the example above has shown no scaling at all. This was definitely laziness...
The next example is essentially the same as the previous one, but it uses a pitch scale which represents the overtone scale, starting at the second partial extending upwards to the 32nd partial. This scale is written into an array by a statement in instrument 0. The durations have fixed possible values which are written into an array (from the longest to the shortest) by hand. The values in both arrays are then called according to their position in the array.
EXAMPLE 01D06_scalings.csd
<CsoundSynthesizer>
<CsOptions>
-d -odac -m0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0
;****POSSIBLE DURATIONS AS ARRAY****
giDurs[] array 3/2, 1, 2/3, 1/2, 1/3, 1/4
giLenDurs lenarray giDurs
;****POSSIBLE PITCHES AS ARRAY****
;initialize array with 31 steps
giScale[] init 31
giLenScale lenarray giScale
;iterate to fill from 65 hz onwards
iStart = 65
iDenom = 3 ;start with 3/2
iCnt = 0
until iCnt = giLenScale do
giScale[iCnt] = iStart
iStart = iStart * iDenom / (iDenom-1)
iDenom += 1 ;next proportion is 4/3 etc
iCnt += 1
enduntil
;****SEQUENCE OF UNITS AS ARRAY****
giSequence[] array 0, 1.2, 1.4, 2.2, 2.4, 3.2, 3.6
giSeqIndx = 0 ;startindex
;****UDO DEFINITIONS****
opcode linrnd_low, i, iii
;linear random with precedence of lower values
iMin, iMax, iMaxCount xin
;set counter and initial (absurd) result
iCount = 0
iRnd = iMax
;loop and reset iRnd
until iCount == iMaxCount do
iUniRnd random iMin, iMax
iRnd = iUniRnd < iRnd ? iUniRnd : iRnd
iCount += 1
enduntil
xout iRnd
endop
opcode linrnd_high, i, iii
;linear random with precedence of higher values
iMin, iMax, iMaxCount xin
;set counter and initial (absurd) result
iCount = 0
iRnd = iMin
;loop and reset iRnd
until iCount == iMaxCount do
iUniRnd random iMin, iMax
iRnd = iUniRnd > iRnd ? iUniRnd : iRnd
iCount += 1
enduntil
xout iRnd
endop
opcode trirnd, i, iii
iMin, iMax, iMaxCount xin
;set a counter and accumulator
iCount = 0
iAccum = 0
;perform loop and accumulate
until iCount == iMaxCount do
iUniRnd random iMin, iMax
iAccum += iUniRnd
iCount += 1
enduntil
;get the mean and output
iRnd = iAccum / iMaxCount
xout iRnd
endop
;****ONE INSTRUMENT TO PERFORM ALL DISTRIBUTIONS****
;0 = uniform, 1 = linrnd_low, 2 = linrnd_high, 3 = trirnd
;the fractional part denotes the number of units, e.g.
;3.4 = triangular distribution with four sub-units
instr notes
;how many notes to be played
iHowMany = p4
;by which distribution with how many units
iWhich = giSequence[giSeqIndx]
iDistrib = int(iWhich)
iUnits = round(frac(iWhich) * 10)
;trigger as many instances of instr play as needed
iThisNote = 0
iStart = 0
iPrint = 1
;for each note to be played
until iThisNote == iHowMany do
;calculate iMidiPch and iDur depending on type
if iDistrib == 0 then
printf_i "%s", iPrint, "... uniform distribution:\n"
printf_i "%s", iPrint, "EQUAL LIKELINESS OF ALL PITCHES AND DURATIONS\n"
iScaleIndx random 0, giLenScale-.0001 ;midi note
iDurIndx random 0, giLenDurs-.0001 ;duration
elseif iDistrib == 1 then
printf_i "... linear low distribution with %d units:\n", iPrint, iUnits
printf_i "%s", iPrint, "LOWER NOTES AND LONGER DURATIONS PREFERRED\n"
iScaleIndx linrnd_low 0, giLenScale-.0001, iUnits
iDurIndx linrnd_low 0, giLenDurs-.0001, iUnits
elseif iDistrib == 2 then
printf_i "... linear high distribution with %d units:\n", iPrint, iUnits
printf_i "%s", iPrint, "HIGHER NOTES AND SHORTER DURATIONS PREFERRED\n"
iScaleIndx linrnd_high 0, giLenScale-.0001, iUnits
iDurIndx linrnd_high 0, giLenDurs-.0001, iUnits
else
printf_i "... triangular distribution with %d units:\n", iPrint, iUnits
printf_i "%s", iPrint, "MEDIUM NOTES AND DURATIONS PREFERRED\n"
iScaleIndx trirnd 0, giLenScale-.0001, iUnits
iDurIndx trirnd 0, giLenDurs-.0001, iUnits
endif
;call subinstrument to play note
iDur = giDurs[int(iDurIndx)]
iPch = giScale[int(iScaleIndx)]
event_i "i", "play", iStart, iDur, iPch
;increase start time and counter
iStart += iDur
iThisNote += 1
;avoid continuous printing
iPrint = 0
enduntil
;reset the duration of this instr to make all events happen
p3 = iStart + 2
;increase index for sequence
giSeqIndx += 1
;call instr again if sequence has not been ended
if giSeqIndx < lenarray(giSequence) then
event_i "i", "notes", p3, 1, iHowMany
;or exit
else
event_i "i", "exit", p3, 1
endif
endin
;****INSTRUMENTS TO PLAY THE SOUNDS AND EXIT CSOUND****
instr play
;increase duration in random range
iDur random p3*2, p3*5
p3 = iDur
;get frequency
iFreq = p4
;generate note with karplus-strong algorithm
aPluck pluck .2, iFreq, iFreq, 0, 1
aPluck linen aPluck, 0, p3, p3
;filter
aFilter mode aPluck, iFreq, .1
;mix aPluck and aFilter according to freq
;(high notes will be filtered more)
aMix ntrpol aPluck, aFilter, iFreq, 65, 65*16
;panning also according to freq
;(low = left, high = right)
iPan = (iFreq-65) / (65*16)
aL, aR pan2 aMix, iPan
outs aL, aR
endin
instr exit
exitnow
endin
</CsInstruments>
<CsScore>
i "notes" 0 1 23 ;set number of notes per instr here
e 99999 ;make possible to perform long (exit will be automatically)
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Random With History
There are many ways a current value in a random number progression can influence the next. Two of them are used frequently. A Markov chain is based on a number of possible states, and defines a different probability for each of these states. A random walk looks at the last state as a position in a range or field, and allows only certain deviations from this position.
Markov Chains
A typical case for a Markov chain in music is a sequence of certain pitches or notes. For each note, the probability of the following note is written in a table like this:

This means: the probability that element a is repeated, is 0.2; the probability that b follows a is 0.5; the probability that c follows a is 0.3. The sum of all probabilities must, by convention, add up to 1. The following example shows the basic algorithm which evaluates the first line of the Markov table above, in the case, the previous element has been 'a'.
EXAMPLE 01D07_markov_basics.csd
<CsoundSynthesizer>
<CsOptions>
-ndm0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
0dbfs = 1
nchnls = 1
seed 0
instr 1
iLine[] array .2, .5, .3
iVal random 0, 1
iAccum = iLine[0]
iIndex = 0
until iAccum >= iVal do
iIndex += 1
iAccum += iLine[iIndex]
enduntil
printf_i "Random number = %.3f, next element = %c!\n", 1, iVal, iIndex+97
endin
</CsInstruments>
<CsScore>
r 10
i 1 0 0
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
The probabilities are 0.2 0.5 0.3. First a uniformly distributed random number between 0 and 1 is generated. An acculumator is set to the first element of the line (here 0.2). It is interrogated as to whether it is larger than the random number. If so then the index is returned, if not, the second element is added (0.2+0.5=0.7), and the process is repeated, until the accumulator is greater or equal the random value. The output of the example should show something like this:
Random number = 0.850, next element = c!
Random number = 0.010, next element = a!
Random number = 0.805, next element = c!
Random number = 0.696, next element = b!
Random number = 0.626, next element = b!
Random number = 0.476, next element = b!
Random number = 0.420, next element = b!
Random number = 0.627, next element = b!
Random number = 0.065, next element = a!
Random number = 0.782, next element = c!
The next example puts this algorithm in an User Defined Opcode. Its input is a Markov table as a two-dimensional array, and the previous line as index (starting with 0). Its output is the next element, also as index. -- There are two Markov chains in this example: seven pitches, and three durations. Both are defined in two-dimensional arrays: giProbNotes and giProbDurs. Both Markov chains are running independently from each other.
EXAMPLE 01D08_markov_music.csd
<CsoundSynthesizer>
<CsOptions>
-dnm128 -odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
0dbfs = 1
nchnls = 2
seed 0
;****USER DEFINED OPCODES FOR MARKOV CHAINS****
opcode Markov, i, i[][]i
iMarkovTable[][], iPrevEl xin
iRandom random 0, 1
iNextEl = 0
iAccum = iMarkovTable[iPrevEl][iNextEl]
until iAccum >= iRandom do
iNextEl += 1
iAccum += iMarkovTable[iPrevEl][iNextEl]
enduntil
xout iNextEl
endop
opcode Markovk, k, k[][]k
kMarkovTable[][], kPrevEl xin
kRandom random 0, 1
kNextEl = 0
kAccum = kMarkovTable[kPrevEl][kNextEl]
until kAccum >= kRandom do
kNextEl += 1
kAccum += kMarkovTable[kPrevEl][kNextEl]
enduntil
xout kNextEl
endop
;****DEFINITIONS FOR NOTES****
;notes as proportions and a base frequency
giNotes[] array 1, 9/8, 6/5, 5/4, 4/3, 3/2, 5/3
giBasFreq = 330
;probability of notes as markov matrix:
;first -> only to third and fourth
;second -> anywhere without self
;third -> strong probability for repetitions
;fourth -> idem
;fifth -> anywhere without third and fourth
;sixth -> mostly to seventh
;seventh -> mostly to sixth
giProbNotes[][] init 7, 7
giProbNotes array 0.0, 0.0, 0.5, 0.5, 0.0, 0.0, 0.0,
0.2, 0.0, 0.2, 0.2, 0.2, 0.1, 0.1,
0.1, 0.1, 0.5, 0.1, 0.1, 0.1, 0.0,
0.0, 0.1, 0.1, 0.5, 0.1, 0.1, 0.1,
0.2, 0.2, 0.0, 0.0, 0.2, 0.2, 0.2,
0.1, 0.1, 0.0, 0.0, 0.1, 0.1, 0.6,
0.1, 0.1, 0.0, 0.0, 0.1, 0.6, 0.1
;****DEFINITIONS FOR DURATIONS****
;possible durations
gkDurs[] array 1, 1/2, 1/3
;probability of durations as markov matrix:
;first -> anything
;second -> mostly self
;third -> mostly second
gkProbDurs[][] init 3, 3
gkProbDurs array 1/3, 1/3, 1/3,
0.2, 0.6, 0.3,
0.1, 0.5, 0.4
;****SET FIRST NOTE AND DURATION FOR MARKOV PROCESS****
giPrevNote init 1
gkPrevDur init 1
;****INSTRUMENT FOR DURATIONS****
instr trigger_note
kTrig metro 1/gkDurs[gkPrevDur]
if kTrig == 1 then
event "i", "select_note", 0, 1
gkPrevDur Markovk gkProbDurs, gkPrevDur
endif
endin
;****INSTRUMENT FOR PITCHES****
instr select_note
;choose next note according to markov matrix and previous note
;and write it to the global variable for (next) previous note
giPrevNote Markov giProbNotes, giPrevNote
;call instr to play this note
event_i "i", "play_note", 0, 2, giPrevNote
;turn off this instrument
turnoff
endin
;****INSTRUMENT TO PERFORM ONE NOTE****
instr play_note
;get note as index in ginotes array and calculate frequency
iNote = p4
iFreq = giBasFreq * giNotes[iNote]
;random choice for mode filter quality and panning
iQ random 10, 200
iPan random 0.1, .9
;generate tone and put out
aImp mpulse 1, p3
aOut mode aImp, iFreq, iQ
aL, aR pan2 aOut, iPan
outs aL, aR
endin
</CsInstruments>
<CsScore>
i "trigger_note" 0 100
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Random Walk
In the context of movement between random values, 'walk' can be thought of as the opposite of 'jump'. If you jump within the boundaries A and B, you can end up anywhere between these boundaries, but if you walk between A and B you will be limited by the extent of your step - each step applies a deviation to the previous one. If the deviation range is slightly more positive (say from -0.1 to +0.2), the general trajectory of your walk will be in the positive direction (but individual steps will not necessarily be in the positive direction). If the deviation range is weighted negative (say from -0.2 to 0.1), then the walk will express a generally negative trajectory.
One way of implementing a random walk will be to take the current state, derive a random deviation, and derive the next state by adding this deviation to the current state. The next example shows two ways of doing this.
The pitch random walk starts at pitch 8 in octave notation. The general pitch deviation gkPitchDev is set to 0.2, so that the next pitch could be between 7.8 and 8.2. But there is also a pitch direction gkPitchDir which is set to 0.1 as initial value. This means that the upper limit of the next random pitch is 8.3 instead of 8.2, so that the pitch will move upwards in a greater number of steps. When the upper limit giHighestPitch has been crossed, the gkPitchDir variable changes from +0.1 to -0.1, so after a number of steps, the pitch will have become lower. Whenever such a direction change happens, the console reports this with a message printed to the terminal.
The density of the notes is defined as notes per second, and is applied as frequency to the metro opcode in instrument 'walk'. The lowest possible density giLowestDens is set to 1, the highest to 8 notes per second, and the first density giStartDens is set to 3. The possible random deviation for the next density is defined in a range from zero to one: zero means no deviation at all, one means that the next density can alter the current density in a range from half the current value to twice the current value. For instance, if the current density is 4, for gkDensDev=1 you would get a density between 2 and 8. The direction of the densities gkDensDir in this random walk follows the same range 0..1. Assumed you have no deviation of densities at all (gkDensDev=0), gkDensDir=0 will produce ticks in always the same speed, whilst gkDensDir=1 will produce a very rapid increase in speed. Similar to the pitch walk, the direction parameter changes from plus to minus if the upper border has crossed, and vice versa.
EXAMPLE 01D09_random_walk.csd
<CsoundSynthesizer>
<CsOptions>
-dnm128 -odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
0dbfs = 1
nchnls = 2
seed 1 ;change to zero for always changing results
;****SETTINGS FOR PITCHES****
;define the pitch street in octave notation
giLowestPitch = 7
giHighestPitch = 9
;set pitch startpoint, deviation range and the first direction
giStartPitch = 8
gkPitchDev init 0.2 ;random range for next pitch
gkPitchDir init 0.1 ;positive = upwards
;****SETTINGS FOR DENSITY****
;define the maximum and minimum density (notes per second)
giLowestDens = 1
giHighestDens = 8
;set first density
giStartDens = 3
;set possible deviation in range 0..1
;0 = no deviation at all
;1 = possible deviation is between half and twice the current density
gkDensDev init 0.5
;set direction in the same range 0..1
;(positive = more dense, shorter notes)
gkDensDir init 0.1
;****INSTRUMENT FOR RANDOM WALK****
instr walk
;set initial values
kPitch init giStartPitch
kDens init giStartDens
;trigger impulses according to density
kTrig metro kDens
;if the metro ticks
if kTrig == 1 then
;1) play current note
event "i", "play", 0, 1.5/kDens, kPitch
;2) calculate next pitch
;define boundaries according to direction
kLowPchBound = gkPitchDir < 0 ? -gkPitchDev+gkPitchDir : -gkPitchDev
kHighPchBound = gkPitchDir > 0 ? gkPitchDev+gkPitchDir : gkPitchDev
;get random value in these boundaries
kPchRnd random kLowPchBound, kHighPchBound
;add to current pitch
kPitch += kPchRnd
;change direction if maxima are crossed, and report
if kPitch > giHighestPitch && gkPitchDir > 0 then
gkPitchDir = -gkPitchDir
printks " Pitch touched maximum - now moving down.\n", 0
elseif kPitch < giLowestPitch && gkPitchDir < 0 then
gkPitchDir = -gkPitchDir
printks "Pitch touched minimum - now moving up.\n", 0
endif
;3) calculate next density (= metro frequency)
;define boundaries according to direction
kLowDensBound = gkDensDir < 0 ? -gkDensDev+gkDensDir : -gkDensDev
kHighDensBound = gkDensDir > 0 ? gkDensDev+gkDensDir : gkDensDev
;get random value in these boundaries
kDensRnd random kLowDensBound, kHighDensBound
;get multiplier (so that kDensRnd=1 yields to 2, and kDens=-1 to 1/2)
kDensMult = 2 ^ kDensRnd
;multiply with current duration
kDens *= kDensMult
;avoid too high values and too low values
kDens = kDens > giHighestDens*1.5 ? giHighestDens*1.5 : kDens
kDens = kDens < giLowestDens/1.5 ? giLowestDens/1.5 : kDens
;change direction if maxima are crossed
if (kDens > giHighestDens && gkDensDir > 0) || (kDens < giLowestDens && gkDensDir < 0) then
gkDensDir = -gkDensDir
if kDens > giHighestDens then
printks " Density touched upper border - now becoming less dense.\n", 0
else
printks " Density touched lower border - now becoming more dense.\n", 0
endif
endif
endif
endin
;****INSTRUMENT TO PLAY ONE NOTE****
instr play
;get note as octave and calculate frequency and panning
iOct = p4
iFreq = cpsoct(iOct)
iPan ntrpol 0, 1, iOct, giLowestPitch, giHighestPitch
;calculate mode filter quality according to duration
iQ ntrpol 10, 400, p3, .15, 1.5
;generate tone and throw out
aImp mpulse 1, p3
aMode mode aImp, iFreq, iQ
aOut linen aMode, 0, p3, p3/4
aL, aR pan2 aOut, iPan
outs aL, aR
endin
</CsInstruments>
<CsScore>
i "walk" 0 999
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
II. SOME MATHS PERSPECTIVES ON RANDOM
Random Processes
The relative frequency of occurrence of a random variable can be described by a probability function (for discrete random variables) or by density functions (for continuous random variables).
When two dice are thrown simultaneously, the sum x of their numbers can be 2, 3, ...12. The following figure shows the probability function p(x) of these possible outcomes. p(x) is always less than or equal to 1. The sum of the probabilities of all possible outcomes is 1.

For continuous random variables the probability of getting a specific value x is 0. But the probability of getting a value within a certain interval can be indicated by an area that corresponds to this probability. The function f(x) over these areas is called the density function. With the following density the chance of getting a number smaller than 0 is 0, to get a number between 0 and 0.5 is 0.5, to get a number between 0.5 and 1 is 0.5 etc. Density functions f(x) can reach values greater than 1 but the area under the function is 1.
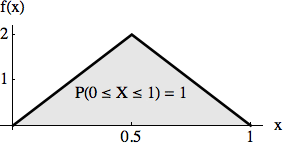
Generating Random Numbers With a Given Probability or Density
Csound provides opcodes for some specific densities but no means to produce random number with user defined probability or density functions. The opcodes rand_density and rand_probability (see below) generate random numbers with probabilities or densities given by tables. They are realized by using the so-called rejection sampling method.
Rejection Sampling:
The principle of rejection sampling is to first generate uniformly distributed random numbers in the range required and to then accept these values corresponding to a given density function (or otherwise reject them). Let us demonstrate this method using the density function shown in the next figure. (Since the rejection sampling method uses only the "shape" of the function, the area under the function need not be 1). We first generate uniformly distributed random numbers rnd1 over the interval [0, 1]. Of these we accept a proportion corresponding to f(rnd1). For example, the value 0.32 will only be accepted in the proportion of f(0.32) = 0.82. We do this by generating a new random number rand2 between 0 and 1 and accept rnd1 only if rand2 < f(rnd1); otherwise we reject it. (see Signals, Systems and Sound Synthesis6 chapter 10.1.4.4)
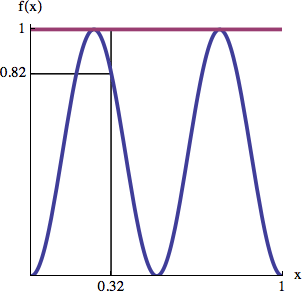
EXAMPLE 01D10_Rejection_Sampling.csd
<CsoundSynthesizer> <CsOptions> -odac </CsOptions> <CsInstruments> ;example by martin neukom sr = 44100 ksmps = 10 nchnls = 1 0dbfs = 1 ; random number generator to a given density function ; kout random number; k_minimum,k_maximum,i_fn for a density function opcode rand_density, k, kki kmin,kmax,ifn xin loop: krnd1 random 0,1 krnd2 random 0,1 k2 table krnd1,ifn,1 if krnd2 > k2 kgoto loop xout kmin+krnd1*(kmax-kmin) endop ; random number generator to a given probability function ; kout random number ; in: i_nr number of possible values ; i_fn1 function for random values ; i_fn2 probability functionExponential: Generate a uniformly distributed number between 0 and 1 and take its natural logarithm. opcode rand_probability, k, iii inr,ifn1,ifn2 xin loop: krnd1 random 0,inr krnd2 random 0,1 k2 table int(krnd1),ifn2,0 if krnd2 > k2 kgoto loop kout table krnd1,ifn1,0 xout kout endop instr 1 krnd rand_density 400,800,2 aout poscil .1,krnd,1 out aout endin instr 2 krnd rand_probability p4,p5,p6 aout poscil .1,krnd,1 out aout endin </CsInstruments> <CsScore> ;sine f1 0 32768 10 1 ;density function f2 0 1024 6 1 112 0 800 0 112 1 ;random values and their relative probability (two dice) f3 0 16 -2 2 3 4 5 6 7 8 9 10 11 12 f4 0 16 2 1 2 3 4 5 6 5 4 3 2 1 ;random values and their relative probability f5 0 8 -2 400 500 600 800 f6 0 8 2 .3 .8 .3 .1 i1 0 10 i2 0 10 4 5 6 </CsScore> </CsoundSynthesizer>
Random Walk
In a series of random numbers the single numbers are independent upon each other. Parameter (left figure) or paths in the room (two-dimensional trajectory in the right figure) created by random numbers wildly jump around.
Example 1
Table[RandomReal[{-1, 1}], {100}];
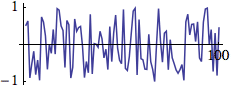
We get a smoother path, a so-called random walk, by adding at every time step a random number r to the actual position x (x += r).
Example 2
x = 0; walk = Table[x += RandomReal[{-.2, .2}], {300}];

The path becomes even smoother by adding a random number r to the actual velocity v.
v += r
x += v
The path can be bounded to an area (figure to the right) by inverting the velocity if the path exceeds the limits (min, max):
vif(x < min || x > max) v *= -1
The movement can be damped by decreasing the velocity at every time step by a small factor d
v *= (1-d)
Example 3
x = 0; v = 0; walk = Table[x += v += RandomReal[{-.01, .01}], {300}];

The path becomes again smoother by adding a random number r to the actual acelleration a, the change of the aceleration, etc.
a += r
v += a
x += v
Example 4
x = 0; v = 0; a = 0;
Table[x += v += a += RandomReal[{-.0001, .0001}], {300}];

(see Martin Neukom, Signals, Systems and Sound Synthesis chapter 10.2.3.2)
EXAMPLE 01D11_Random_Walk2.csd
<CsoundSynthesizer> <CsOptions> -odac </CsOptions> <CsInstruments> ;example by martin neukom sr = 44100 ksmps = 128 nchnls = 1 0dbfs = 1 ; random frequency instr 1 kx random -p6, p6 kfreq = p5*2^kx aout oscil p4, kfreq, 1 out aout endin ; random change of frequency instr 2 kx init .5 kfreq = p5*2^kx kv random -p6, p6 kv = kv*(1 - p7) kx = kx + kv aout oscil p4, kfreq, 1 out aout endin ; random change of change of frequency instr 3 kv init 0 kx init .5 kfreq = p5*2^kx ka random -p7, p7 kv = kv + ka kv = kv*(1 - p8) kx = kx + kv kv = (kx < -p6 || kx > p6?-kv : kv) aout oscili p4, kfreq, 1 out aout endin </CsInstruments> <CsScore> f1 0 32768 10 1 ; i1 p4 p5 p6 ; i2 p4 p5 p6 p7 ; amp c_fr rand damp ; i2 0 20 .1 600 0.01 0.001 ; amp c_fr d_fr rand damp ; amp c_fr rand ; i1 0 20 .1 600 0.5 ; i3 p4 p5 p6 p7 p8 i3 0 20 .1 600 1 0.001 0.001 </CsScore> </CsoundSynthesizer>
III. MISCELLANEOUS EXAMPLES
Csound has a range of opcodes and GEN routine for the creation of various random functions and distributions. Perhaps the simplest of these is random which simply generates a random value within user defined minimum and maximum limit and at i-time, k-rate or a-rate accroding to the variable type of its output:
ires random imin, imax kres random kmin, kmax ares random kmin, kmax
Values are generated according to a uniform random distribution, meaning that any value within the limits has equal chance of occurence. Non-uniform distributions in which certain values have greater chance of occurence over others are often more useful and musical. For these purposes, Csound includes the betarand, bexprand, cauchy, exprand, gauss, linrand, pcauchy, poisson, trirand, unirand and weibull random number generator opcodes. The distributions generated by several of these opcodes are illustrated below.

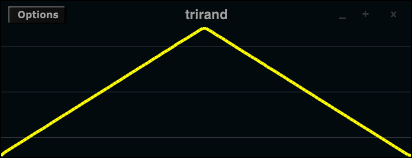
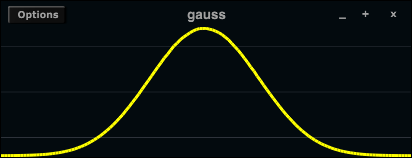
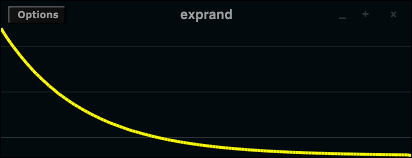
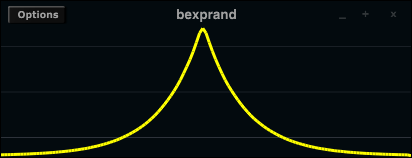

In addition to these so called 'x-class noise generators' Csound provides random function generators, providing values that change over time a various ways.
randomh generates new random numbers at a user defined rate. The previous value is held until a new value is generated, and then the output immediately assumes that value.
The instruction:
kmin = -1 kmax = 1 kfreq = 2 kout randomh kmin,kmax,kfreq
will produce and output something like:
randomi is an interpolating version of randomh. Rather than jump to new values when they are generated, randomi interpolates linearly to the new value, reaching it just as a new random value is generated. Replacing randomh with randomi in the above code snippet would result in the following output:
In practice randomi's angular changes in direction as new random values are generated might be audible depending on the how it is used. rsplsine (or the simpler jsplsine) allows us to specify not just a single frequency but a minimum and a maximum frequency, and the resulting function is a smooth spline between the minimum and maximum values and these minimum and maximum frequencies. The following input:
kmin = -0.95 kmax = 0.95 kminfrq = 1 kmaxfrq = 4 asig rspline kmin, kmax, kminfrq, kmaxfrq
would generate an output something like:
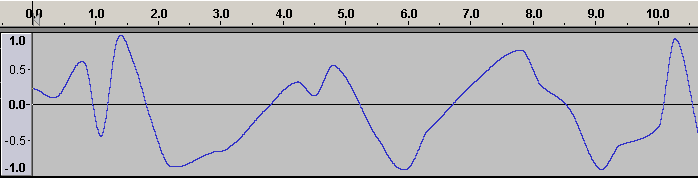
We need to be careful with what we do with rspline's output as it can exceed the limits set by kmin and kmax. Minimum and maximum values can be set conservatively or the limit opcode could be used to prevent out of range values that could cause problems.
The following example uses rspline to 'humanise' a simple synthesiser. A short melody is played, first without any humanising and then with humanising. rspline random variation is added to the amplitude and pitch of each note in addition to an i-time random offset.
EXAMPLE 01D12_humanising.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0
giWave ftgen 0, 0, 2^10, 10, 1,0,1/4,0,1/16,0,1/64,0,1/256,0,1/1024
instr 1 ; an instrument with no 'humanising'
inote = p4
aEnv linen 0.1,0.01,p3,0.01
aSig poscil aEnv,cpsmidinn(inote),giWave
outs aSig,aSig
endin
instr 2 ; an instrument with 'humanising'
inote = p4
; generate some i-time 'static' random paramters
iRndAmp random -3,3 ; amp. will be offset by a random number of decibels
iRndNte random -5,5 ; note will be offset by a random number of cents
; generate some k-rate random functions
kAmpWob rspline -1,1,1,10 ; amplitude 'wobble' (in decibels)
kNteWob rspline -5,5,0.3,10 ; note 'wobble' (in cents)
; calculate final note function (in CPS)
kcps = cpsmidinn(inote+(iRndNte*0.01)+(kNteWob*0.01))
; amplitude envelope (randomisation of attack time)
aEnv linen 0.1*ampdb(iRndAmp+kAmpWob),0.01+rnd(0.03),p3,0.01
aSig poscil aEnv,kcps,giWave
outs aSig,aSig
endin
</CsInstruments>
<CsScore>
t 0 80
#define SCORE(i) #
i $i 0 1 60
i . + 2.5 69
i . + 0.5 67
i . + 0.5 65
i . + 0.5 64
i . + 3 62
i . + 1 62
i . + 2.5 70
i . + 0.5 69
i . + 0.5 67
i . + 0.5 65
i . + 3 64 #
$SCORE(1) ; play melody without humanising
b 17
$SCORE(2) ; play melody with humanising
e
</CsScore>
</CsoundSynthesizer>
;example by Iain McCurdy
The final example implements a simple algorithmic note generator. It makes use of GEN17 to generate histograms which define the probabilities of certain notes and certain rhythmic gaps occuring.
EXAMPLE 01D13_simple_algorithmic_note_generator.csd
<CsoundSynthesizer>
<CsOptions>
-odac -dm0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giNotes ftgen 0,0,-100,-17,0,48, 15,53, 30,55, 40,60, 50,63, 60,65, 79,67, 85,70, 90,72, 96,75
giDurs ftgen 0,0,-100,-17,0,2, 30,0.5, 75,1, 90,1.5
instr 1
kDur init 0.5 ; initial rhythmic duration
kTrig metro 2/kDur ; metronome freq. 2 times inverse of duration
kNdx trandom kTrig,0,1 ; create a random index upon each metro 'click'
kDur table kNdx,giDurs,1 ; read a note duration value
schedkwhen kTrig,0,0,2,0,1 ; trigger a note!
endin
instr 2
iNote table rnd(1),giNotes,1 ; read a random value from the function table
aEnv linsegr 0, 0.005, 1, p3-0.105, 1, 0.1, 0 ; amplitude envelope
iPlk random 0.1, 0.3 ; point at which to pluck the string
iDtn random -0.05, 0.05 ; random detune
aSig wgpluck2 0.98, 0.2, cpsmidinn(iNote+iDtn), iPlk, 0.06
out aSig * aEnv
endin
</CsInstruments>
<CsScore>
i 1 0 300 ; start 3 long notes close after one another
i 1 0.01 300
i 1 0.02 300
e
</CsScore>
</CsoundSynthesizer>
;example by Iain McCurdy
- http://www.etymonline.com/index.php?term=random^
- Because the sample rate is 44100 samples per second. So a repetition after 65536 samples will lead to a repetition after 65536/44100 = 1.486 seconds.^
- Charles Dodge and Thomas A. Jerse, Computer Music, New York 1985, Chapter 8.1, in particular page 269-278.^
- Most of them have been written by Paris Smaragdis in 1995: betarnd, bexprnd, cauchy, exprnd, gauss, linrand, pcauchy, poisson, trirand, unirand and weibull.^
- According to Dodge/Jerse, the usual algorithms for exponential and gaussian are:
Exponential: Generate a uniformly distributed number between 0 and 1 and take its natural logarithm.
Gauss: Take the mean of uniformly distributed numbers and scale them by the standard deviation. ^ - Neukom, Martin. Signals, systems and sound synthesis. Bern: Peter Lang, 2013. Print. ^
02 QUICK START
MAKE CSOUND RUN
Csound and Frontends
The core element of Csound is an audio engine for the Csound language. It has no graphical interface and it is designed to take Csound text files (called ".csd" files) and produce audio, either in realtime, or by writing to a file. It can still be used in this way but most users nowadays prefer to use Csound via a frontend. A frontend is an application which assists you in writing code and running Csound. Beyond the functions of a simple text editor, a frontend environment will offer colour coded highlighting of language specific keywords and quick access to an integrated help system. A frontend can also expand possibilities by providing tools to build interactive interfaces (GUI widgets) as well, sometimes, as advanced compositional tools.
In 2009 the Csound developers decided to include CsoundQt as the standard frontend to be included with the Csound distribution, so you will already have this frontend if you have installed any of the pre-built versions of Csound. Conversely if you install a frontend you will usually require a separate installation of Csound in order for it to function. If you experience any problems with CsoundQt, or simply prefer another frontend design, try Cabbage, WinXound or Blue as alternatives. Section 10 of this manual provides more information about the frontends.
How to Download and Install Csound
To get Csound you first need to download the package for your system from the Download page of the Csound project on Github: http://csound.github.io/download.html
There are many files here, so here are some guidelines to help you choose the appropriate version.
Windows
Windows installers are the ones ending in .exe. Look for the latest version of Csound and find a file which should be called something like: Setup_Csound6_6.07.0beta.exe.
After you have downloaded the installer simply double-click it start the installation process. This will invoke 8 simple steps:
- A welcome screen advises you to close other programs.
- After reading and accepting the licence agreement click 'Next'.
- Select the destination for the Csound program files. The default is C:\Program Files (x86)\Csound6.
- Choose the components to be installed. Currently (ver. 6.07) there are only 3 items: Core Csound is obligatory. Python features are optional but will be required if you intend to use CsoundQt as a frontend for Csound. You will also need to install Python 2.7. Pure data Csound~ object will allow you to run Csound from within Pure Data. To do this will require installing Pure Data.
- Select Start Menu Folder allows you to define a folder name other than the default 'Csound 6' for the folder containing the various Csound components. Alternatively you can choose not to create a start menu folder.
- Next there is an option to add the Csoound application directory to your PATH variable. Adding this will allow you to run Csound from the command line from any directory location.
- Next a window reminds you of what will be installed and what changes will be made to your system.
- Upon clicking install the installation takes place.
- A window informs you that installation is complete. You can click 'Finish'.
This installer will also automatically install CsoundQt which can be used as a frontend for your work with Csound (Csound is not run by double-clicking Csound.exe).
You can create addional shorcuts to the CsoundQt executable by locating it in its default location, C:\Program Files (x86)\Csound6\bin, and right-clicking it and selecting 'Pin to Start' or 'Pin to Taskbar' as desired. You can create a desktop shortcut by right-clicking and dragging the CsoundQt executable onto the desktop and selecting 'Create Shortcuts Here' from the menu that pops up.
Other frontends for Csound, such as Cabbage and WinXound, need to be downloaded and installed separately.
Mac OS X
The Mac OS X installers are the files ending in .dmg. Look for the latest version of Csound for your particular system, for example a Universal binary for 10.9 will be called something like: csound6.06-OSX-universal.dmg. When you double click the downloaded file, you will have a disk image on your desktop, with the Csound installer, CsoundQt and a readme file. Double-click the installer and follow the instructions. Csound and the basic Csound utilities will be installed. To install the CsoundQt frontend, you only need to move it to your Applications folder.
Linux and others
Csound is available from the official package repositories for many distributions like OpenSuse, Debian, Ubuntu, Fedora, Archlinux and Gentoo. If there are no binary packages for your platform, or you need a more recent version, you can get the sources from the Github page and build from source. You will find the most recent build instructions in the Build.md file in the Csound sources or in the Github Csound Wiki.
iOS
If you would just like to run Csound on your iPad, there is an app for iOS called CsoundPad:
http://itunes.apple.com/app/csoundpad/id861008380?mt=8#
If you are a developer, Csound can be run in an iOS app that you are programming by including the Csound-for-iOS files in your Xcode project. For example for version 6.09 of Csound, the files are in this archive:
http://github.com/csound/csound/releases/download/6.09.1/csound-iOS-6.09.1.zip
The "csound-iOS-6.09.1.zip" file contains an archive of an example project and PDF manual.
Some sample projects:
- AudioKit (http://audiokit.io) is an Objective-C and Swift framework for building iOS and OSX apps using Csound as the audio engine.
- csGrain, developed by the Boulanger Labs (http://www.boulangerlabs.com), is a complex audio effects app that works with audio files or live audio input.
- Portable Dandy, an innovative sampler synthesiser for iOS (see http://www.barefoot-coders.com).
- iPulsaret, an impressive synthesizer app (see http://www.densitytigs.com).
Android
If you want to play your .csd files on your Android smartphone or tablet, follow the "Android App" link on Csound's Download page. This leads you to Google's Play Store from which you can install it for free. Chapter 12F in this manual describes how to use Csound on Android.
If you are a developer, download the Android SDK, for instance:
http://github.com/csound/csound/releases/download/6.09.1/csound-android-6.09.1.zip
On Google's Play Store there are some apps that use Csound. Below is a small sample of such apps:
- DIY Sound Salad, developed by Zatchu (http://zatchu.com/category/story/), is a multi sample record and playback app. Quite enjoyable to use.
- Chime Pad, developed by Arthur B. Hunkins (http://www.arthunkins.com), is a soothing chime player app.
- Psycho Flute developed by Brian Redfern (source code available at http://github.com/bredfern/PsychoFlute), it is a "physical modelling flute synth". Both fun and interesting.
Install Problems?
If, for any reason, you can't find the CsoundQt frontend on your system after install, or if you want to install the most recent version of CsoundQt, or if you prefer another frontend altogether: see the CSOUND FRONTENDS section of this manual for further information. If you have any install problems, consider joining the Csound Mailing List to report your issues, or write a mail to one of the maintainers (see ON THIS RELEASE).
The Csound Reference Manual
The Csound Reference Manual is an indispensable companion to Csound. It is available in various formats from the same place as the Csound installers, and it is installed with the packages for OS X and Windows. It can also be browsed online at http://csound.github.io/docs/manual/index.html. Many frontends will provide you with direct and easy access to it.
How to Execute a Simple Example
Using CsoundQt
Launch CsoundQt. Go into the CsoundQt menubar and choose: Examples->Getting started...-> Basics-> HelloWorld
You will see a very basic Csound file (.csd) with a lot of comments in green.
Click on the "RUN" icon in the CsoundQt control bar to start the realtime Csound engine. You should hear a 440 Hz sine wave.
You can also run the Csound engine in the terminal from within CsoundQt. Just click on "Run in Term". A console will pop up and Csound will be executed as an independent process. The result should be the same - the 440 Hz "beep".
Using the Terminal / Console
1. Save the following code in any plain text editor as HelloWorld.csd.
EXAMPLE 02A01_HelloWorld.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Alex Hofmann
instr 1
aSin poscil 0dbfs/4, 440
out aSin
endin
</CsInstruments>
<CsScore>
i 1 0 1
</CsScore>
</CsoundSynthesizer>
2. Open the Terminal / Prompt / Console
3. Type: csound /full/path/HelloWorld.csd
where /full/path/HelloWorld.csd is the complete path to your file. You also execute this file by just typing csound then dragging the file into the terminal window and then hitting return.
You should hear a 440 Hz tone.
Using Cabbage
Cabbage is an alternative frontend for working with Csound. It is most similar to CsoundQt but its main differences with CsoundQt are that graphical user interface (GUI) can be created either by drawing (click and drag) or by typing code. In CsoundQt the GUI code is 'hidden' from us in the editor so that we only create GUI using the mouse. Cabbage can also export instruments and effects as VST and AU plugins, and even includes its own host, Cabbage Studio, for graphically connecting multiple instruments and effect in a manner similar to Pure Data. Cabbage is a less comprehensive frontend that CsoundQt but some users prefer this simplicity.
To get started with Cabbage you will need to first download Cabbage. Cabbage will normally come bundled with its own version of Csound and will not require a separate installation of Csound. Any currently installed versions of Csound will be ignored by Cabbage.
Once installed, launch Cabbage and then go to Options->New Cabbage...->Instrument to create a new patch (called a Cabbage patch). Cabbage will start you off with a simple functional instrument with a virtual keyboard but you can also use the one listed below which features a virtual keyboard and a volume control. To open Cabbage's integrated code editor go to Options->View Source Editor. You can then paste in the code shown below, or just make modifications to the default instrument code. If you want to make changes to what external hardware devices Cabbage uses, such as audio and MIDI hardware, go to Options->Audio Settings. The options available will vary depending on your specific system, so will not be discussed any further here.
When creating a realtime instrument, there is no necessity to include any Csound score events (or any <score> tags). With earlier versions of Csound it used to be that we needed to include a 'dummy' score event to keep realtime performance going but with more recent versions of Csound this is no longer the case.
The key element that differentiates Cabbage from standard Csound is the inclusion of Cabbage specific code, mainly used for creating a graphical user interface, held within the start and end tags: <Cabbage> and </Cabbage>. Communication from the Cabbage GUI to Csound is either transparent, as in the case of the 'keyboard' widget, or via named channels and the chnget opcode in the Csound orchestra when using most other Cabbage widgets such as 'rslider' (a rotary slider). For additional information on Cabbage please consult the chapter on Cabbage.
EXAMPLE 02A02_HelloCabbage.csd
<Cabbage>
form size(420,100)
keyboard bounds(10,10,300,80)
rslider bounds(325,15,80,80), channel("level"), text("Level"), range(0,1,0.3)
</Cabbage>
<CsoundSynthesizer>
<CsOptions>
-dm0 -n -+rtmidi=null -M0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1
icps cpsmidi
klev chnget "level"
a1 poscil klev*0.2,icps
outs a1,a1
endin
</CsInstruments>
</CsoundSynthesizer>
CSOUND SYNTAX
Orchestra and Score
In Csound, you must define "instruments", which are units which "do things", for instance creating a sine wave as audio signal and play it (= output it to the audio card). These instruments must be called or "turned on" by a "score". The Csound "score" is a list of events which describe how the instruments are to be played in time. It can be thought of as a timeline in text.
A Csound instrument is contained within an Instrument Block, which starts with the keyword instr and ends with the keyword endin. All instruments are given a number (or a name) to identify them.
instr 1 ... instrument instructions come here... endin
Score events in Csound are individual text lines, which can turn on instruments for a certain time. For example, to turn on instrument 1, at time 0, for 2 seconds you will use:
i 1 0 2
Note that orchestra and score are two completely different types of code. The orchestra contains the actual Csound code.1 The instruments are written in the Csound Programming Language. The score is mainly a list of events. The Score Language is poor and offers only some very basic tools.
In modern Csound code, the score often remains empty. The events derive from orchestra code,2 or from real-time interaction, like MIDI, OSC, mouse clicks or any other live input.
The Csound Document Structure
A Csound document is structured into three main sections:
- CsOptions: Contains the configuration options for Csound. For example using "-o dac" in this section will make Csound run in real-time instead of writing a sound file.
- CsInstruments: Contains the instrument definitions and optionally some global settings and definitions like sample rate, etc.
- CsScore: Contains the score events which trigger the instruments.
Each of these sections is opened with a <xyz> tag and closed with a </xyz> tag. Every Csound file starts with the <CsoundSynthesizer> tag, and ends with </CsoundSynthesizer>. Only the text in-between will be used by Csound.
EXAMPLE 02B01_DocStruct.csd
<CsoundSynthesizer>; START OF A CSOUND FILE
<CsOptions> ; CSOUND CONFIGURATION
-odac
</CsOptions>
<CsInstruments> ; INSTRUMENT DEFINITIONS GO HERE
; Set the audio sample rate to 44100 Hz
sr = 44100
instr 1
; a 440 Hz Sine Wave
aSin poscil 0dbfs/4, 440
out aSin
endin
</CsInstruments>
<CsScore> ; SCORE EVENTS GO HERE
i 1 0 1
</CsScore>
</CsoundSynthesizer> ; END OF THE CSOUND FILE
; Anything after a semicolon is ignored by Csound
Comments, which are lines of text that Csound will ignore, are started with the ";" character. Multi-line comments can be made by encasing them between "/*" and "*/".
Opcodes
"Opcodes" or "Unit generators" are the basic building blocks of Csound. Opcodes can do many things like produce oscillating signals, filter signals, perform mathematical functions or even turn on and off instruments. Opcodes, depending on their function, will take inputs and outputs. Each input or output is called, in programming terms, an "argument". Opcodes always take input arguments on the right and output their results on the left, like this:
output OPCODE input1, input2, input3, .., inputN
For example the poscil opcode has two mandatory inputs:3 amplitude and frequency, and produces a sine wave signal:
aSin poscil 0dbfs/4, 440
In this case, a 440 Hertz oscillation with an amplitude of 0dbfs/4 (a quarter of 0 dB as full scale) will be created and its output will be stored in a container called aSin. The order of the arguments is important: the first input to poscil will always be amplitude and the second input will always be read by Csound as frequency.
Since Csound6, the code can be written in a way which is knows from many other programming languages:3
aSin = poscil(0dbfs/4,440)
Many opcodes include optional input arguments and occasionally optional output arguments. These will always be placed after the essential arguments. In the Csound Manual documentation they are indicated using square brackets "[]". If optional input arguments are omitted they are replaced with the default values indicated in the Csound Manual. The addition of optional output arguments normally initiates a different mode of that opcode: for example, a stereo as opposed to mono version of the opcode.
Variables
A "variable" is a named container. It is a place to store things like signals or values from where they can be recalled by using their name. In Csound there are various types of variables. The easiest way to deal with variables when getting to know Csound is to imagine them as cables.
If you want to patch this together:
Sound Generator -> Filter -> Output,
you need two cables, one going out from the generator into the filter and one from the filter to the output. The cables carry audio signals, which are variables beginning with the letter "a".
aSource buzz 0.8, 200, 10, 1
aFiltered moogladder aSource, 400, 0.8
out aFiltered
In the example above, the buzz opcode produces a complex waveform as signal aSource. This signal is fed into the moogladder opcode, which in turn produces the signal aFiltered. The out opcode takes this signal, and sends it to the output whether that be to the speakers or to a rendered file.
Other common variable types are "k" variables which store control signals, which are updated less frequently than audio signals, and "i" variables which are constants within each instrument note.
You can find more information about variable types here in this manual, or here in the Csound Journal.
Using the Manual
The Csound Reference Manual is a comprehensive source regarding Csound's syntax and opcodes. All opcodes have their own manual entry describing their syntax and behavior, and the manual contains a detailed reference on the Csound language and options.
In CsoundQt you can find the Csound Manual in the Help Menu. You can quickly go to a particular opcode entry in the manual by putting the cursor on the opcode and pressing Shift+F1. WinXsound , Cabbage and Blue also provide easy access to the manual.
- Its characteristics are described in detail in section 03 CSOUND LANGUAGE. ^
- For instance using the schedule or event opcode. ^
- For details, see chapter 03I about Functional Syntax. ^
CONFIGURING MIDI
Csound can receive MIDI events (like MIDI notes and MIDI control changes) from an external MIDI interface or from another program via a virtual MIDI cable. This information can be used to control any aspect of synthesis or performance.
Most frontends are using their own MIDI handler. See the chapters about CsoundQt, Cabbage and Blue in this manual, or have a look at the built-in documentation of these environments. The following description is only relevant when you use Csound's own MIDI handlers, for instance when running Csound via Command Line.
Csound receives MIDI data through MIDI Realtime Modules. These are special Csound plugins which enable MIDI input using different methods according to a specific platform. They are enabled using the -+rtmidi command line flag in the <CsOptions> section of your .csd file.
There is the universal "portmidi" module. PortMidi is a cross-platform module for MIDI I/O and should be available on all platforms. To enable the "portmidi" module, use the flag (option):
-+rtmidi=portmidi
After selecting the RT MIDI module from a front-end or the command line, you need to select the MIDI devices for input and output. These are set using the flags -M and -Q respectively followed by the number of the interface. You can usually use:
-M999
To get a performance error with a listing of available interfaces.
For the PortMidi module (and others like ALSA), you can specify no number to use the default MIDI interface or the 'a' character to use all devices (which is actually the most common case). This will even work when no MIDI devices are present.
-Ma
So if you want MIDI input using the portmidi module, using device 2 for input and device 1 for output, your <CsOptions> section should contain:
-+rtmidi=portmidi -M2 -Q1
There is a special "virtual" RT MIDI module which enables MIDI input from a virtual keyboard. To enable it, you can use:
-+rtmidi=virtual -M0
Platform Specific Modules
If the "portmidi" module is not working properly for some reason, you can try other platform specific modules.
Linux
On Linux systems, you might also have an "alsa" module to use the alsa raw MIDI interface. This is different from the more common alsa sequencer interface and will typically require the snd-virmidi module to be loaded.
OS X
On OS X you may have a "coremidi" module available.
Windows
On Windows, you may have a "winmme" MIDI module.
How to Use a MIDI Keyboard
Once you've set up the hardware, you are ready to receive MIDI information and interpret it in Csound. By default, when a MIDI note is received, it turns on the Csound instrument corresponding to its channel number, so if a note is received on channel 3, it will turn on instrument 3, if it is received on channel 10, it will turn on instrument 10 and so on.
If you want to change this routing of MIDI channels to instruments, you can use the massign opcode. For instance, this statement lets you route your MIDI channel 1 to instrument 10:
massign 1, 10
On the following example, a simple instrument, which plays a sine wave, is defined in instrument 1. There are no score note events, so no sound will be produced unless a MIDI note is received on channel 1.
EXAMPLE 02C01_Midi_Keybd_in.csd
<CsoundSynthesizer>
<CsOptions>
-+rtmidi=portmidi -Ma -odac
</CsOptions>
<CsInstruments>
;Example by Andrés Cabrera
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
massign 0, 1 ;assign all MIDI channels to instrument 1
instr 1
iCps cpsmidi ;get the frequency from the key pressed
iAmp ampmidi 0dbfs * 0.3 ;get the amplitude
aOut poscil iAmp, iCps ;generate a sine tone
outs aOut, aOut ;write it to the output
endin
</CsInstruments>
<CsScore>
</CsScore>
</CsoundSynthesizer>
Note that Csound has an unlimited polyphony in this way: each key pressed starts a new instance of instrument 1, and you can have any number of instrument instances at the same time.
How to Use a MIDI Controller
To receive MIDI controller events, opcodes like ctrl7 can be used. In the following example instrument 1 is turned on for 60 seconds. It will receive controller #1 (modulation wheel) on channel 1 and convert MIDI range (0-127) to a range between 220 and 440. This value is used to set the frequency of a simple sine oscillator.
EXAMPLE 02C02_Midi_Ctl_in.csd
<CsoundSynthesizer>
<CsOptions>
-+rtmidi=virtual -M1 -odac
</CsOptions>
<CsInstruments>
;Example by Andrés Cabrera
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1
; --- receive controller number 1 on channel 1 and scale from 220 to 440
kFreq ctrl7 1, 1, 220, 440
; --- use this value as varying frequency for a sine wave
aOut poscil 0.2, kFreq
outs aOut, aOut
endin
</CsInstruments>
<CsScore>
i 1 0 60
</CsScore>
</CsoundSynthesizer>
Other Type of MIDI Data
Csound can receive other type of MIDI, like pitch bend, and aftertouch through the usage of specific opcodes. Generic MIDI Data can be received using the midiin opcode. The example below prints to the console the data received via MIDI.
EXAMPLE 02C03_Midi_all_in.csd
<CsoundSynthesizer>
<CsOptions>
-+rtmidi=portmidi -Ma -odac
</CsOptions>
<CsInstruments>
;Example by Andrés Cabrera
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1
kStatus, kChan, kData1, kData2 midiin
if kStatus != 0 then ;print if any new MIDI message has been received
printk 0, kStatus
printk 0, kChan
printk 0, kData1
printk 0, kData2
endif
endin
</CsInstruments>
<CsScore>
i1 0 3600
</CsScore>
</CsoundSynthesizer>
LIVE AUDIO
Similar to the MIDI configuration, the standard Csound frontends CsoundQt, Cabbage and Blue all provide their own way how to configure audio. The following description is useful to understand what happens behind the curtains, and must be regarded if you use Csound via Command Line.
Select the Audio Device
Csound relates to the various inputs and outputs of sound devices installed on your computer as a numbered list. If you wish to send or receive audio to or from a specific audio connection you will need to know the number by which Csound knows it. If you are not sure of what that is you can trick Csound into providing you with a list of available devices by trying to run Csound using an obviously out of range device number, like this:
EXAMPLE 02D01_GetDeviceList.csd
<CsoundSynthesizer> <CsOptions> -iadc999 -odac999 </CsOptions> <CsInstruments> ;Example by Andrés Cabrera instr 1 endin </CsInstruments> <CsScore> </CsScore> </CsoundSynthesizer>
The input (-i) and output (-o) devices will be listed seperately.1 Specify your input device with the -iadc flag and the number of your input device, and your output device with the -odac flag and the number of your output device. For instance, if you select one of the devices from the list above both, for input and output, you may include something like
-iadc2 -odac3
in the <CsOptions> section of your .csd file.
If you do not specify any device number, the default device of your system configuration will be used by Csound. So usually it is sufficient to write:
-iadc -odac
If you have no real-time (microphone) input, you only need to declare -odac. Without this option, Csound will not produce real-time audio output, but write to an audio file as output instead.
Select the Audio Driver
The RT (= real-time) output module can be set with the -+rtaudio flag. If you don't use this flag, the PortAudio driver will be used. Other possible drivers are jack and alsa (Linux), mme (Windows) or CoreAudio (Mac). So, this sets your audio driver to mme instead of Port Audio:
-+rtaudio=mme
Tuning Performance and Latency
Live performance and latency depend mainly on the sizes of the software and the hardware buffers. They can be set in the <CsOptions> using the -B flag for the hardware buffer, and the -b flag for the software buffer.2 For instance, this statement sets the hardware buffer size to 512 samples and the software buffer size to 128 sample:
-B512 -b128
The other factor which affects Csound's live performance is the ksmps value which is set in the header of the <CsInstruments> section. By this value, you define how many samples are processed every Csound control cycle.
Try your realtime performance with -B512, -b128 and ksmps=32.3 With a software buffer of 128 samples, a hardware buffer of 512 and a sample rate of 44100 you will have around 12ms latency, which is usable for live keyboard playing. If you have problems with either the latency or the performance, tweak the values as described here.
The "--realtime" Option
When you have instruments that have substantial sections that could block out execution, for instance with code that loads buffers from files or creates big tables, you can try the option --realtime.
This option will give your audio processing the priority over other tasks to be done. It places all initialisation code on a separate thread, and does not block the audio thread. Instruments start performing only after all the initialisation is done. That can have a side-effect on scheduling if your audio input and output buffers are not small enough, because the audio processing thread may “run ahead” of the initialisation one, taking advantage of any slack in the buffering.
Given that this option is intrinsically linked to low-latency, realtime audio performance, and also to reduce the effect on scheduling these other tasks, it is recommended that small ksmps and buffer sizes, for example ksmps=16, 32, or 64, -b32 or 64, and -B256 or 512.
Csound Can Produce Extreme Dynamic Range!
Csound can produce extreme dynamic range, so keep an eye on the level you are sending to your output. The number which describes the level of 0 dB, can be set in Csound by the 0dbfs assignment in the <CsInstruments> header. There is no limitation, if you set 0dbfs = 1 and send a value of 32000, this can damage your ears and speakers!
Using Live Audio Input and Output
To process audio from an external source (for example a microphone), use the inch opcode to access any of the inputs of your audio input device. For the output, outch gives you all necessary flexibility. The following example takes a live audio input and transforms its sound using ring modulation. The Csound Console should output five times per second the input amplitude level.
EXAMPLE 02D02_LiveInput.csd
<CsoundSynthesizer>
<CsOptions>
;CHANGE YOUR INPUT AND OUTPUT DEVICE NUMBER HERE IF NECESSARY!
-iadc -odac -B512 -b128
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100 ;set sample rate to 44100 Hz
ksmps = 32 ;number of samples per control cycle
nchnls = 2 ;use two audio channels
0dbfs = 1 ;set maximum level as 1
instr 1
aIn inch 1 ;take input from channel 1
kInLev downsamp aIn ;convert audio input to control signal
printk .2, abs(kInLev)
;make modulator frequency oscillate 200 to 1000 Hz
kModFreq poscil 400, 1/2
kModFreq = kModFreq+600
aMod poscil 1, kModFreq ;modulator signal
aRM = aIn * aMod ;ring modulation
outch 1, aRM, 2, aRM ;output to channel 1 and 2
endin
</CsInstruments>
<CsScore>
i 1 0 3600
</CsScore>
</CsoundSynthesizer>
Live Audio is frequently used with live devices like widgets or MIDI. You will find various examples in the example collections of your preferred frontend.
- You may have to run -iadc999 and -odac999 seperately.^
- As Victor Lazzarini explains (mail to Joachim Heintz, 19 march 2013), the role of -b and -B varies between the Audio Modules:
"1. For portaudio, -B is only used to suggest a latency to the backend, whereas -b is used to set the actual buffersize.
2. For coreaudio, -B is used as the size of the internal circular buffer, and -b is used for the actual IO buffer size.
3. For jack, -B is used to determine the number of buffers used in conjunction with -b , num = (N + M + 1) / M. -b is the size of each buffer.
4. For alsa, -B is the size of the buffer size, -b is the period size (a buffer is divided into periods).
5. For pulse, -b is the actual buffersize passed to the device, -B is not used.
In other words, -B is not too significant in 1), not used in 5), but has a part to play in 2), 3) and 4), which is functionally similar." ^ - It is always preferable to use power-of-two values for ksmps (which is the same as "block size" in PureData or "vector size" in Max). Just with ksmps = 1, 2, 4, 8, 16 ... you will take advantage of the "full duplex" audio, which provides best real time audio. Make sure your ksmps divides your buffer size with no remainder. So, for -b 128, you can use ksmps = 128, 64, 32, 16, 8, 4, 2 or 1.^
RENDERING TO FILE
When to Render to File
Csound can also render audio straight to a sound file stored on your hard drive instead of as live audio sent to the audio hardware. This gives you the possibility to hear the results of very complex processes which your computer can't produce in realtime. Or you want to render something in Csound to import it in an audio editor, or as the final result of a 'tape' piece.1
Csound can render to formats like wav, aiff or ogg (and other less popular ones), but not mp3 due to its patent and licencing problems.
Rendering to File
Save the following code as Render.csd:
EXAMPLE 02E01_Render.csd
<CsoundSynthesizer>
<CsOptions>
-o Render.wav
</CsOptions>
<CsInstruments>
;Example by Alex Hofmann
instr 1
aSin poscil 0dbfs/4, 440
out aSin
endin
</CsInstruments>
<CsScore>
i 1 0 1
</CsScore>
</CsoundSynthesizer>
Open the Terminal / Prompt / Console and type:
csound /path/to/Render.csd
Now, because you changed the -o flag in the <CsOptions> from "-o dac" to "-o filename", the audio output is no longer written in realtime to your audio device, but instead to a file. The file will be rendered to the default directory (usually the user home directory). This file can be opened and played in any audio player or editor, e.g. Audacity.
The -o flag can also be used to write the output file to a certain directory. Something like this for Windows ...
<CsOptions> -o c:/music/samples/Render.wav </CsOptions>
... and this for Linux or Mac OSX:
<CsOptions> -o /Users/JSB/organ/tatata.wav </CsOptions>
Rendering Options
The internal rendering of audio data in Csound is done with 64-bit floating point numbers. Depending on your needs, you should decide the precision of your rendered output file:
- If you want to render 32-bit floats, use the option flag -f.
- If you want to render 24-bit, use the flag -3 (= 3 bytes).
- If you want to render 16-bit, use the flag -s (or nothing, because this is also the default in Csound).
For making sure that the header of your soundfile will be written correctly, you should use the -W flag for a WAV file, or the -A flag for a AIFF file. So these options will render the file "Wow.wav" as WAV file with 24-bit accuracy:
<CsOptions> -o Wow.wav -W -3 </CsOptions>
Realtime and Render-To-File at the Same Time
Sometimes you may want to simultaneously have realtime output and file rendering to disk, like recording your live performance. This can be achieved by using the fout opcode. You just have to specify your output file name. File type and format are given by a number, for instance 18 specifies "wav 24 bit" (see the manual page for more information). The following example creates a random frequency and panning movement of a sine wave, and writes it to the file "live_record.wav" (in the same directory as your .csd file):
EXAMPLE 02E02_RecordRT.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0 ;each time different seed for random
instr 1
kFreq randomi 400, 800, 1 ;random sliding frequency
aSig poscil .2, kFreq ;sine with this frequency
kPan randomi 0, 1, 1 ;random panning
aL, aR pan2 aSig, kPan ;stereo output signal
outs aL, aR ;live output
fout "live_record.wav", 18, aL, aR ;write to soundfile
endin
</CsInstruments>
<CsScore>
i 1 0 10
</CsScore>
</CsoundSynthesizer>
03 CSOUND LANGUAGE
INITIALIZATION AND PERFORMANCE PASS
Not only for beginners, but also for experienced Csound users, many problems result from the misunderstanding of the so-called i-rate and k-rate. You want Csound to do something just once, but Csound does it continuously. You want Csound to do something continuously, but Csound does it just once. If you experience such a case, you will most probably have confused i- and k-rate-variables.
The concept behind this is actually not complicated. But it is something which is more implicitly mentioned when we think of a program flow, whereas Csound wants to know it explicitely. So we tend to forget it when we use Csound, and we do not notice that we ordered a stone to become a wave, and a wave to become a stone. This chapter tries to explicate very carefully the difference between stones and waves, and how you can profit from them, after you understood and accepted both qualities.
The Init Pass
Whenever a Csound instrument is called, all variables are set to initial values. This is called the initialization pass.
There are certain variables, which stay in the state in which they have been put by the init-pass. These variables start with an i if they are local (= only considered inside an instrument), or with a gi if they are global (= considered overall in the orchestra). This is a simple example:
EXAMPLE 03A01_Init-pass.csd
<CsoundSynthesizer>
<CsInstruments>
giGlobal = 1/2
instr 1
iLocal = 1/4
print giGlobal, iLocal
endin
instr 2
iLocal = 1/5
print giGlobal, iLocal
endin
</CsInstruments>
<CsScore>
i 1 0 0
i 2 0 0
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
The output should include these lines:
SECTION 1:
new alloc for instr 1:
instr 1: giGlobal = 0.500 iLocal = 0.250
new alloc for instr 2:
instr 2: giGlobal = 0.500 iLocal = 0.200
As you see, the local variables iLocal do have different meanings in the context of their instrument, whereas giGlobal is known everywhere and in the same way. It is also worth mentioning that the performance time of the instruments (p3) is zero. This makes sense, as the instruments are called, but only the init-pass is performed.1
The Performance Pass
After having assigned initial values to all variables, Csound starts the actual performance. As music is a variation of values in time,2 audio signals are producing values which vary in time. In all digital audio, the time unit is given by the sample rate, and one sample is the smallest possible time atom. For a sample rate of 44100 Hz,3 one sample comes up to the duration of 1/44100 = 0.0000227 seconds.
So, performance for an audio application means basically: calculate all the samples which are finally being written to the output. You can imagine this as the cooperation of a clock and a calculator. For each sample, the clock ticks, and for each tick, the next sample is calculated.
Most audio applications do not perform this calculation sample by sample. It is much more efficient to collect some amount of samples in a "block" or "vector", and calculate them all together. This means in fact, to introduce another internal clock in your application; a clock which ticks less frequently than the sample clock. For instance, if (always assumed your sample rate is 44100 Hz) your block size consists of 10 samples, your internal calculation time clock ticks every 1/4410 (0.000227) seconds. If your block size consists of 441 samples, the clock ticks every 1/100 (0.01) seconds.
The following illustration shows an example for a block size of 10 samples. The samples are shown at the bottom line. Above are the control ticks, one for each ten samples. The top two lines show the times for both clocks in seconds. In the upmost line you see that the first control cycle has been finished at 0.000227 seconds, the second one at 0.000454 seconds, and so on.4 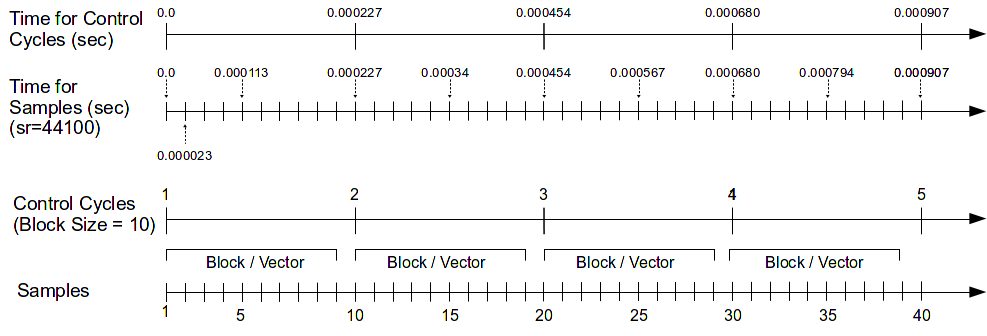
The rate (frequency) of these ticks is called the control rate in Csound. By historical reason,5 it is called "kontrol rate" instead of control rate, and abbreviated as "kr" instead of cr. Each of the calculation cycles is called a "k-cycle". The block size or vector size is given by the ksmps parameter, which means: how many samples (smps) are collected for one k-cycle.6
Let us see some code examples to illustrate these basic contexts.
Implicit Incrementation
EXAMPLE 03A02_Perf-pass_incr.csd
<CsoundSynthesizer> <CsInstruments> sr = 44100 ksmps = 4410 instr 1 kCount init 0; set kcount to 0 first kCount = kCount + 1; increase at each k-pass printk 0, kCount; print the value endin </CsInstruments> <CsScore> i 1 0 1 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
Your output should contain the lines:
i 1 time 0.10000: 1.00000
i 1 time 0.20000: 2.00000
i 1 time 0.30000: 3.00000
i 1 time 0.40000: 4.00000
i 1 time 0.50000: 5.00000
i 1 time 0.60000: 6.00000
i 1 time 0.70000: 7.00000
i 1 time 0.80000: 8.00000
i 1 time 0.90000: 9.00000
i 1 time 1.00000: 10.00000
A counter (kCount) is set here to zero as initial value. Then, in each control cycle, the counter is increased by one. What we see here, is the typical behaviour of a loop. The loop has not been set explicitely, but works implicitely because of the continuous recalculation of all k-variables. So we can also speak about the k-cycles as an implicit (and time-triggered) k-loop.7 Try changing the ksmps value from 4410 to 8820 and to 2205 and observe the difference.
The next example reads the incrementation of kCount as rising frequency. The first instrument, called Rise, sets the k-rate frequency kFreq to the initial value of 100 Hz, and then adds 10 Hz in every new k-cycle. As ksmps=441, one k-cycle takes 1/100 second to perform. So in 3 seconds, the frequency rises from 100 to 3100 Hz. At the last k-cycle, the final frequency value is printed out.8 - The second instrument, Partials, increments the counter by one for each k-cycle, but only sets this as new frequency for every 100 steps. So the frequency stays at 100 Hz for one second, then at 200 Hz for one second, and so on. As the resulting frequencies are in the ratio 1 : 2 : 3 ..., we hear partials based on a 100 Hz fundamental, from the first partial up to the 31st. The opcode printk2 prints out the frequency value whenever it has changed.
EXAMPLE 03A03_Perf-pass_incr_listen.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr = 44100 ksmps = 441 0dbfs = 1 nchnls = 2 ;build a table containing a sine wave giSine ftgen 0, 0, 2^10, 10, 1 instr Rise kFreq init 100 aSine poscil .2, kFreq, giSine outs aSine, aSine ;increment frequency by 10 Hz for each k-cycle kFreq = kFreq + 10 ;print out the frequency for the last k-cycle kLast release if kLast == 1 then printk 0, kFreq endif endin instr Partials ;initialize kCount kCount init 100 ;get new frequency if kCount equals 100, 200, ... if kCount % 100 == 0 then kFreq = kCount endif aSine poscil .2, kFreq, giSine outs aSine, aSine ;increment kCount kCount = kCount + 1 ;print out kFreq whenever it has changed printk2 kFreq endin </CsInstruments> <CsScore> i "Rise" 0 3 i "Partials" 4 31 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
Init versus Equals
A frequently occuring error is that instead of setting the k-variable as kCount init 0, it is set as kCount = 0. The meaning of both statements has one significant difference. kCount init 0 sets the value for kCount to zero only in the init pass, without affecting it during the performance pass. kCount = 1 sets the value for kCount to zero again and again, in each performance cycle. So the increment always starts from the same point, and nothing really happens:
EXAMPLE 03A04_Perf-pass_no_incr.csd
<CsoundSynthesizer> <CsInstruments> sr = 44100 ksmps = 4410 instr 1 kcount = 0; sets kcount to 0 at each k-cycle kcount = kcount + 1; does not really increase ... printk 0, kcount; print the value endin </CsInstruments> <CsScore> i 1 0 1 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
Outputs:
i 1 time 0.10000: 1.00000
i 1 time 0.20000: 1.00000
i 1 time 0.30000: 1.00000
i 1 time 0.40000: 1.00000
i 1 time 0.50000: 1.00000
i 1 time 0.60000: 1.00000
i 1 time 0.70000: 1.00000
i 1 time 0.80000: 1.00000
i 1 time 0.90000: 1.00000
i 1 time 1.00000: 1.00000
A Look at the Audio Vector
There are different opcodes to print out k-variables.9 There is no opcode in Csound to print out the audio vector directly, but you can use the vaget opcode to see what is happening inside one control cycle with the audio samples.
EXAMPLE 03A05_Audio_vector.csd
<CsoundSynthesizer> <CsInstruments> sr = 44100 ksmps = 5 0dbfs = 1 instr 1 aSine oscils 1, 2205, 0 kVec1 vaget 0, aSine kVec2 vaget 1, aSine kVec3 vaget 2, aSine kVec4 vaget 3, aSine kVec5 vaget 4, aSine printks "kVec1 = % f, kVec2 = % f, kVec3 = % f, kVec4 = % f, kVec5 = % f\n",\ 0, kVec1, kVec2, kVec3, kVec4, kVec5 endin </CsInstruments> <CsScore> i 1 0 [1/2205] </CsScore> </CsoundSynthesizer> ;example by joachim heintz
The output shows these lines:
kVec1 = 0.000000, kVec2 = 0.309017, kVec3 = 0.587785, kVec4 = 0.809017, kVec5 = 0.951057
kVec1 = 1.000000, kVec2 = 0.951057, kVec3 = 0.809017, kVec4 = 0.587785, kVec5 = 0.309017
kVec1 = -0.000000, kVec2 = -0.309017, kVec3 = -0.587785, kVec4 = -0.809017, kVec5 = -0.951057
kVec1 = -1.000000, kVec2 = -0.951057, kVec3 = -0.809017, kVec4 = -0.587785, kVec5 = -0.309017
In this example, the number of audio samples in one k-cycle is set to five by the statement ksmps=5. The first argument to vaget specifies which sample of the block you get. For instance,
kVec1 vaget 0, aSine
gets the first value of the audio vector and writes it into the variable kVec1. For a frequency of 2205 Hz at a sample rate of 44100 Hz, you need 20 samples to write one complete cycle of the sine. So we call the instrument for 1/2205 seconds, and we get 4 k-cycles. The printout shows exactly one period of the sine wave.
At the end of this chapter we will show another and more advances method to access the audio vector and modify its samples.
A Summarizing Example
After having put so much attention to the different single aspects of initialization, performance and audio vectors, the next example tries to summarize and illustrate all the aspects in their practical mixture.
EXAMPLE 03A06_Init_perf_audio.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 441
nchnls = 2
0dbfs = 1
instr 1
iAmp = p4 ;amplitude taken from the 4th parameter of the score line
iFreq = p5 ;frequency taken from the 5th parameter
; --- move from 0 to 1 in the duration of this instrument call (p3)
kPan line 0, p3, 1
aNote oscils iAmp, iFreq, 0 ;create an audio signal
aL, aR pan2 aNote, kPan ;let the signal move from left to right
outs aL, aR ;write it to the output
endin
</CsInstruments>
<CsScore>
i 1 0 3 0.2 443
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
As ksmps=441, each control cycle is 0.01 seconds long (441/44100). So this happens when the instrument call is performed:

Accessing the Initialization Value of a k-Variable
It has been said that the init pass sets initial values to all variables. It must be emphasized that this indeed concerns all variables, not only the i-variables. It is only the matter that i-variables are not affected by anything which happens later, in the performance. But also k- and a-variables get their initial values.
As we saw, the init opcode is used to set initial values for k- or a-variables explicitely. On the other hand, you can get the initial value of a k-variable which has not been set explicitely, by the i() facility. This is a simple example:
EXAMPLE 03A07_Init-values_of_k-variables.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> instr 1 gkLine line 0, p3, 1 endin instr 2 iInstr2LineValue = i(gkLine) print iInstr2LineValue endin instr 3 iInstr3LineValue = i(gkLine) print iInstr3LineValue endin </CsInstruments> <CsScore> i 1 0 5 i 2 2 0 i 3 4 0 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
Outputs:
new alloc for instr 1:
B 0.000 .. 2.000 T 2.000 TT 2.000 M: 0.0
new alloc for instr 2:
instr 2: iInstr2LineValue = 0.400
B 2.000 .. 4.000 T 4.000 TT 4.000 M: 0.0
new alloc for instr 3:
instr 3: iInstr3LineValue = 0.800
B 4.000 .. 5.000 T 5.000 TT 5.000 M: 0.0
Instrument 1 produces a rising k-signal, starting at zero and ending at one, over a time of five seconds. The values of this line rise are written to the global variable gkLine. After two seconds, instrument 2 is called, and examines the value of gkLine at its init-pass via i(gkLine). The value at this time (0.4), is printed out at init-time as iInstr2LineValue. The same happens for instrument 3, which prints out iInstr3LineValue = 0.800, as it has been started at 4 seconds.
The i() feature is particularily useful if you need to examine the value of any control signal from a widget or from midi, at the time when an instrument starts.
For getting the init value of an element in a k-time array, see the section "More on Array Rates" in the Arrays chapter of this book.
k-Values and Initialization in Multiple Triggered Instruments
What happens on a k-variable if an instrument is called multiple times? What is the initialization value of this variable on the first call, and on the subsequent calls?
If this variable is not set explicitely, the init value in the first call of an instrument is zero, as usual. But, for the next calls, the k-variable is initialized to the value which was left when the previous instance of the same instrument turned off.
The following example shows this behaviour. Instrument "Call" simply calls the instrument "Called" once a second, and sends the number of the call to it. Instrument "Called" generates the variable kRndVal by a random generator, and reports both:
- the value of kRndVal at initialization, and
- the value of kRndVal at performance time, i.e. the first control cycle.
(After the first k-cycle, the instrument is turned off immediately.)
EXAMPLE 03A08_k-inits_in_multiple_calls_1.csd
<CsoundSynthesizer> <CsOptions> -nm0 </CsOptions> <CsInstruments> ksmps = 32 instr Call kNumCall init 1 kTrig metro 1 if kTrig == 1 then event "i", "Called", 0, 1, kNumCall kNumCall += 1 endif endin instr Called iNumCall = p4 kRndVal random 0, 10 prints "Initialization value of kRnd in call %d = %.3f\n", iNumCall, i(kRndVal) printks " New random value of kRnd generated in call %d = %.3f\n", 0, iNumCall, kRndVal turnoff endin </CsInstruments> <CsScore> i "Call" 0 3 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
The output should show this:
Initialization value of kRnd in call 1 = 0.000
New random value of kRnd generated in call 1 = 8.829
Initialization value of kRnd in call 2 = 8.829
New random value of kRnd generated in call 2 = 2.913
Initialization value of kRnd in call 3 = 2.913
New random value of kRnd generated in call 3 = 9.257
The printout shows what was stated before: If there is no previous value of a k-variable, this variable is initialized to zero. If there is a previous value, it serves as initialization value.
But is this init-value of a k-variable of any relevance? Actually, we choose a k-value because we want to use it at performance-time, not at init-time. — Well, the problem is that Csound *will* perform the init-pass for all k- (and a-) variables, unless you prevent it from doing this explicitely. And if you, for example, generate an array index in the previous instance of the same instrument, which is out of range at initialization, Csound will report an error, or even crash:
EXAMPLE 03A09_k-inits_in_multiple_calls_2.csd
<CsoundSynthesizer> <CsOptions> -nm0 </CsOptions> <CsInstruments> ksmps = 32 gkArray[] fillarray 1, 2, 3, 5, 8 instr Call kNumCall init 1 kTrig metro 1 if kTrig == 1 then event "i", "Called", 0, 1, kNumCall kNumCall += 1 endif endin instr Called ;get the number of the instrument instance iNumCall = p4 ;set the start index for the while-loop kIndex = 0 ;get the init value of kIndex prints "Initialization value of kIndx in call %d = %d\n", iNumCall, i(kIndex) ;perform the while-loop until kIndex equals five while kIndex < lenarray(gkArray) do printf "Index %d of gkArray has value %d\n", kIndex+1, kIndex, gkArray[kIndex] kIndex += 1 od ;last value of kIndex is 5 because of increment printks " Last value of kIndex in call %d = %d\n", 0, iNumCall, kIndex ;turn this instance off after first k-cycle turnoff endin </CsInstruments> <CsScore> i "Call" 0 1 ;change performance time to 2 to get an error! </CsScore> </CsoundSynthesizer> ;example by joachim heintz
When you change the performance time to 2 instead of 1, you will get an error, because the array will be asked for index=5. (But, as the length of this array is 5, the last index is 4.) This will be the output in this case:
Initialization value of kIndx in call 1 = 0
Index 0 of gkArray has value 1
Index 1 of gkArray has value 2
Index 2 of gkArray has value 3
Index 3 of gkArray has value 5
Index 4 of gkArray has value 8
Last value of kIndex in call 1 = 5
Initialization value of kIndx in call 2 = 5
PERF ERROR in instr 2: Array index 5 out of range (0,4) for dimension 1
note aborted
The problem is that the expression gkArray[kIndex] is performed *at init-time*. And, that the expression kIndex=0 has no effect at all to the value of kIndex *at init-time*. If we want to be sure that kIndex is zero also at init-time, we must write this explicitely by
kIndex init 0
Note that this is *exactly* the same for User-Defined Opcodes! If you call a UDO twice, it will have the current value of a k-Variable of the first call as init-value of the second call, unless you initialize the k-variable explicitely by an init statement.
The final example shows both possibilities, using explicit initialization or not, and the resulting effect.
EXAMPLE 03A10_k-inits_in_multiple_calls_3.csd
<CsoundSynthesizer> <CsOptions> -nm0 </CsOptions> <CsInstruments> ksmps = 32 instr without_init prints "instr without_init, call %d:\n", p4 kVal = 1 prints " Value of kVal at initialization = %d\n", i(kVal) printks " Value of kVal at first k-cycle = %d\n", 0, kVal kVal = 2 turnoff endin instr with_init prints "instr with_init, call %d:\n", p4 kVal init 1 kVal = 1 prints " Value of kVal at initialization = %d\n", i(kVal) printks " Value of kVal at first k-cycle = %d\n", 0, kVal kVal = 2 turnoff endin </CsInstruments> <CsScore> i "without_init" 0 .1 1 i "without_init" + .1 2 i "with_init" 1 .1 1 i "with_init" + .1 2 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
This is the output:
instr without_init, call 1:
Value of kVal at initialization = 0
Value of kVal at first k-cycle = 1
instr without_init, call 2:
Value of kVal at initialization = 2
Value of kVal at first k-cycle = 1
instr with_init, call 1:
Value of kVal at initialization = 1
Value of kVal at first k-cycle = 1
instr with_init, call 2:
Value of kVal at initialization = 1
Value of kVal at first k-cycle = 1
Note that this characteristics of using "leftovers" from previous instances which may lead to undesired effects, does also occur for audio variables. Similar to k-variables, an audio vector is initalized for the first instance to zero, or to the value which is explcitely set by an init statement. In case a previous instance can be re-used, its last state will be the init state of the new instance.
The next example shows an undesired side effect in instrument 1. In the third call (start=2), the previous values for the a1 audio vector will be used, because this variable is not set explicitely. This means, though, that 32 amplitudes are repeated in a frequency of sr/ksmps, in this case 44100/32 = 1378.125 Hz. The same happens at start=4 with audio variable a2. Instrument 2 initializes a1 and a2 in the cases they need to be, so that the inadvertend tone disappears.
EXAMPLE 03A11_a_inits_in_multiple_calls.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32 ;try 64 or other values
nchnls = 2
0dbfs = 1
instr 1 ;without explicit init
i1 = p4
if i1 == 0 then
a1 poscil 0.5, 500
endif
if i1 == 1 then
a2 poscil 0.5, 600
endif
outs a1, a2
endin
instr 2 ;with explicit init
i1 = p4
if i1 == 0 then
a1 poscil 0.5, 500
a2 init 0
endif
if i1 == 1 then
a2 poscil 0.5, 600
a1 init 0
endif
outs a1, a2
endin
</CsInstruments>
<CsScore>
i 1 0 .5 0
i . 1 . 0
i . 2 . 1
i . 3 . 1
i . 4 . 0
i . 5 . 0
i . 6 . 1
i . 7 . 1
b 9
i 2 0 .5 0
i . 1 . 0
i . 2 . 1
i . 3 . 1
i . 4 . 0
i . 5 . 0
i . 6 . 1
i . 7 . 1
</CsScore>
</CsoundSynthesizer>
;example by oeyvind brandtsegg and joachim heintz
Reinitialization
As we saw above, an i-value is not affected by the performance loop. So you cannot expect this to work as an incrementation:
EXAMPLE 03A12_Init_no_incr.csd
<CsoundSynthesizer> <CsInstruments> sr = 44100 ksmps = 4410 instr 1 iCount init 0 ;set iCount to 0 first iCount = iCount + 1 ;increase print iCount ;print the value endin </CsInstruments> <CsScore> i 1 0 1 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
The output is nothing but:
instr 1: iCount = 1.000
But you can advise Csound to repeat the initialization of an i-variable. This is done with the reinit opcode. You must mark a section by a label (any name followed by a colon). Then the reinit statement will cause the i-variable to refresh. Use rireturn to end the reinit section.
EXAMPLE 03A13_Re-init.csd
<CsoundSynthesizer> <CsInstruments> sr = 44100 ksmps = 4410 instr 1 iCount init 0 ; set icount to 0 first reinit new ; reinit the section each k-pass new: iCount = iCount + 1 ; increase print iCount ; print the value rireturn endin </CsInstruments> <CsScore> i 1 0 1 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
Outputs:
instr 1: iCount = 1.000
instr 1: iCount = 2.000
instr 1: iCount = 3.000
instr 1: iCount = 4.000
instr 1: iCount = 5.000
instr 1: iCount = 6.000
instr 1: iCount = 7.000
instr 1: iCount = 8.000
instr 1: iCount = 9.000
instr 1: iCount = 10.000
instr 1: iCount = 11.000
What happens here more in detail, is the following. In the actual init-pass, iCount is set to zero via iCount init 0. Still in this init-pass, it is incremented by one (iCount = iCount+1) and the value is printed out as iCount = 1.000. Now starts the first performance pass. The statement reinit new advices Csound to initialise again the section labeled as "new". So the statement iCount = iCount + 1 is executed again. As the current value of iCount at this time is 1, the result is 2. So the printout at this first performance pass is iCount = 2.000. The same happens in the next nine performance cycles, so the final count is 11.
Order Of Calculation
In this context, it can be very important to observe the order in which the instruments of a Csound orchestra are evaluated. This order is determined by the instrument numbers. So, if you want to use during the same performance pass a value in instrument 10 which is generated by another instrument, you must not give this instrument the number 11 or higher. In the following example, first instrument 10 uses a value of instrument 1, then a value of instrument 100.
EXAMPLE 03A14_Order_of_calc.csd
<CsoundSynthesizer> <CsInstruments> sr = 44100 ksmps = 4410 instr 1 gkcount init 0 ;set gkcount to 0 first gkcount = gkcount + 1 ;increase endin instr 10 printk 0, gkcount ;print the value endin instr 100 gkcount init 0 ;set gkcount to 0 first gkcount = gkcount + 1 ;increase endin </CsInstruments> <CsScore> ;first i1 and i10 i 1 0 1 i 10 0 1 ;then i100 and i10 i 100 1 1 i 10 1 1 </CsScore> </CsoundSynthesizer> ;Example by Joachim Heintz
The output shows the difference:
new alloc for instr 1:
new alloc for instr 10:
i 10 time 0.10000: 1.00000
i 10 time 0.20000: 2.00000
i 10 time 0.30000: 3.00000
i 10 time 0.40000: 4.00000
i 10 time 0.50000: 5.00000
i 10 time 0.60000: 6.00000
i 10 time 0.70000: 7.00000
i 10 time 0.80000: 8.00000
i 10 time 0.90000: 9.00000
i 10 time 1.00000: 10.00000
B 0.000 .. 1.000 T 1.000 TT 1.000 M: 0.0
new alloc for instr 100:
i 10 time 1.10000: 0.00000
i 10 time 1.20000: 1.00000
i 10 time 1.30000: 2.00000
i 10 time 1.40000: 3.00000
i 10 time 1.50000: 4.00000
i 10 time 1.60000: 5.00000
i 10 time 1.70000: 6.00000
i 10 time 1.80000: 7.00000
i 10 time 1.90000: 8.00000
i 10 time 2.00000: 9.00000
B 1.000 .. 2.000 T 2.000 TT 2.000 M: 0.0
Instrument 10 can use the values which instrument 1 has produced in the same control cycle, but it can only refer to values of instrument 100 which are produced in the previous control cycle. By this reason, the printout shows values which are one less in the latter case.
Named Instruments
It has been said in chapter 02B (Quick Start) that instead of a number you can also use a name for an instrument. This is mostly preferable, because you can give meaningful names, leading to a better readable code. But what about the order of calculation in named instruments?
The answer is simple: Csound calculates them in the same order as they are written in the orchestra. So if your instrument collection is like this ...
EXAMPLE 03A15_Order_of_calc_named.csd
<CsoundSynthesizer> <CsOptions> -nd </CsOptions> <CsInstruments> instr Grain_machine prints " Grain_machine\n" endin instr Fantastic_FM prints " Fantastic_FM\n" endin instr Random_Filter prints " Random_Filter\n" endin instr Final_Reverb prints " Final_Reverb\n" endin </CsInstruments> <CsScore> i "Final_Reverb" 0 1 i "Random_Filter" 0 1 i "Grain_machine" 0 1 i "Fantastic_FM" 0 1 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
... you can count on this output:
new alloc for instr Grain_machine:
Grain_machine
new alloc for instr Fantastic_FM:
Fantastic_FM
new alloc for instr Random_Filter:
Random_Filter
new alloc for instr Final_Reverb:
Final_Reverb
Note that the score has not the same order. But internally, Csound transforms all names to numbers, in the order they are written from top to bottom. The numbers are reported on the top of Csound's output:10
instr Grain_machine uses instrument number 1
instr Fantastic_FM uses instrument number 2
instr Random_Filter uses instrument number 3
instr Final_Reverb uses instrument number 4
About "i-time" And "k-rate" Opcodes
It is often confusing for the beginner that there are some opcodes which only work at "i-time" or "i-rate", and others which only work at "k-rate" or "k-time". For instance, if the user wants to print the value of any variable, (s)he thinks: "OK - print it out." But Csound replies: "Please, tell me first if you want to print an i- or a k-variable".11
The print opcode just prints variables which are updated at each initialization pass ("i-time" or "i-rate"). If you want to print a variable which is updated at each control cycle ("k-rate" or "k-time"), you need its counterpart printk. (As the performance pass is usually updated some thousands times per second, you have an additional parameter in printk, telling Csound how often you want to print out the k-values.)
So, some opcodes are just for i-rate variables, like filelen or ftgen. Others are just for k-rate variables like metro or max_k. Many opcodes have variants for either i-rate-variables or k-rate-variables, like printf_i and printf, sprintf and sprintfk, strindex and strindexk.
Most of the Csound opcodes are able to work either at i-time or at k-time or at audio-rate, but you have to think carefully what you need, as the behaviour will be very different if you choose the i-, k- or a-variante of an opcode. For example, the random opcode can work at all three rates:
ires random imin, imax : works at "i-time" kres random kmin, kmax : works at "k-rate" ares random kmin, kmax : works at "audio-rate"
If you use the i-rate random generator, you will get one value for each note. For instance, if you want to have a different pitch for each note you are generating, you will use this one.
If you use the k-rate random generator, you will get one new value on every control cycle. If your sample rate is 44100 and your ksmps=10, you will get 4410 new values per second! If you take this as pitch value for a note, you will hear nothing but a noisy jumping. If you want to have a moving pitch, you can use the randomi variant of the k-rate random generator, which can reduce the number of new values per second, and interpolate between them.
If you use the a-rate random generator, you will get as many new values per second as your sample rate is. If you use it in the range of your 0 dB amplitude, you produce white noise.
EXAMPLE 03A16_Random_at_ika.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
0dbfs = 1
nchnls = 2
seed 0 ;each time different seed
giSine ftgen 0, 0, 2^10, 10, 1 ;sine table
instr 1 ;i-rate random
iPch random 300, 600
aAmp linseg .5, p3, 0
aSine poscil aAmp, iPch, giSine
outs aSine, aSine
endin
instr 2 ;k-rate random: noisy
kPch random 300, 600
aAmp linseg .5, p3, 0
aSine poscil aAmp, kPch, giSine
outs aSine, aSine
endin
instr 3 ;k-rate random with interpolation: sliding pitch
kPch randomi 300, 600, 3
aAmp linseg .5, p3, 0
aSine poscil aAmp, kPch, giSine
outs aSine, aSine
endin
instr 4 ;a-rate random: white noise
aNoise random -.1, .1
outs aNoise, aNoise
endin
</CsInstruments>
<CsScore>
i 1 0 .5
i 1 .25 .5
i 1 .5 .5
i 1 .75 .5
i 2 2 1
i 3 4 2
i 3 5 2
i 3 6 2
i 4 9 1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Possible Problems with k-Rate Tick Size
It has been said that usually the k-rate clock ticks much slower than the sample (a-rate) clock. For a common size of ksmps=32, one k-value remains the same for 32 samples. This can lead to problems, for instance if you use k-rate envelopes. Let us assume that you want to produce a very short fade-in of 3 milliseconds, and you do it with the following line of code:
kFadeIn linseg 0, .003, 1
Your envelope will look like this:

Such a "staircase-envelope" is what you hear in the next example as zipper noise. The transeg opcode produces a non-linear envelope with a sharp peak:
The rise and the decay are each 1/100 seconds long. If this envelope is produced at k-rate with a blocksize of 128 (instr 1), the noise is clearly audible. Try changing ksmps to 64, 32 or 16 and compare the amount of zipper noise. - Instrument 2 uses an envelope at audio-rate instead. Regardless the blocksize, each sample is calculated seperately, so the envelope will always be smooth.
EXAMPLE 03A17_Zipper.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
;--- increase or decrease to hear the difference more or less evident
ksmps = 128
nchnls = 2
0dbfs = 1
instr 1 ;envelope at k-time
aSine oscils .5, 800, 0
kEnv transeg 0, .1, 5, 1, .1, -5, 0
aOut = aSine * kEnv
outs aOut, aOut
endin
instr 2 ;envelope at a-time
aSine oscils .5, 800, 0
aEnv transeg 0, .1, 5, 1, .1, -5, 0
aOut = aSine * aEnv
outs aOut, aOut
endin
</CsInstruments>
<CsScore>
r 5 ;repeat the following line 5 times
i 1 0 1
s ;end of section
r 5
i 2 0 1
e
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Time Impossible
There are two internal clocks in Csound. The sample rate (sr) determines the audio-rate, whereas the control rate (kr) determines the rate, in which a new control cycle can be started and a new block of samples can be performed. In general, Csound can not start any event in between two control cycles, nor end.
The next example chooses an extreme small control rate (only 10 k-cycles per second) to illustrate this.
EXAMPLE 03A18_Time_Impossible.csd
<CsoundSynthesizer> <CsOptions> -o test.wav -d </CsOptions> <CsInstruments> sr = 44100 ksmps = 4410 nchnls = 1 0dbfs = 1 instr 1 aPink oscils .5, 430, 0 out aPink endin </CsInstruments> <CsScore> i 1 0.05 0.1 i 1 0.4 0.15 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
The first call advices instrument 1 to start performance at time 0.05. But this is impossible as it lies between two control cycles. The second call starts at a possible time, but the duration of 0.15 again does not coincident with the control rate. So the result starts the first call at time 0.1 and extends the second call to 0.2 seconds:
With Csound6, the possibilities of these "in between" are enlarged via the --sample-accurate option. The next image shows how a 0.01 second envelope which is generated by the code
a1 init 1 a2 linen a1, p3/3, p3, p3/3 out a2
(and a call of 0.01 seconds at sr=44100) shows up in the following cases:
- ksmps=128
- ksmps=32
- ksmps=1
- ksmps=128 and --sample-accurate enabled

This is the effect:
- At ksmps=128, the last section of the envelope is missing. The reason is that, at sr=44100 Hz, 0.01 seconds contain 441 samples. 441 samples divided by the block size (ksmps) of 128 samples yield to 3.4453125 blocks. This is rounded to 3. So only 3 * 128 = 384 Samples are performed. As you see, the envelope itself is calculated correctly in its shape. It would end exactly at 0.01 seconds .. but it does not, because the ksmps block ends too early. So this envelope might introduce a click at the end of this note.
- At ksmps=32, the number of samples (441) divided by ksmps yield to a value of 13.78125. This is rounded to 14, so the rendered audio is slightly longer than 0.01 seconds (448 samples).
- At ksmps=1, the envelope is as expected.
- At ksmps=128 and --sample-accurate enabled, the envelope is correct, too. Note that the section is now 4*128=512 samples long, but the envelope is more accurate than at ksmps=32.
So, in case you experience clicks at very short envelopes although you use a-rate envelopes, it might be necessary to set either ksmps=1, or to enable the --sample-accurate option.
Yet another Look at the Audio Vector
In Csound 6 it is actually possible to access each sample of the audio vector directly, without setting ksmps=1. This feature, however, requires some knowledge about arrays and loops, so beginners should skip this paragraph.
The direct access uses the a...[] syntax which is common in most programming languages for arrays or lists. As an audio vector is of ksmps length, we must iterate in each k-cycle over it. By this, we can both, get and modify the values of the single samples directly. Moreover, we can use control structures which are usually k-rate only also at a-rate, for instance any condition depending on the value of a single sample.
The next example demonstrates three different usages of the sample-by-sample processing. In the "SimpleTest" instrument, every single sample is multiplied by a value (1, 3 and -1). Then the result is added to the previous sample value. This leads to amplification for iFac=3 and to silence for iFac=-1 because in this case every sample cancels itself. In the "PrintSampleIf" instrument, each sample which is between 0.99 and 1.00 is printed to the console. Also in the "PlaySampleIf" instrument an if-condition is applied on each sample, but here not for printing rather than playing out only the samples whichs values are between 0 and 1/10000. They are then multiplied by 10000 so that not only rhythm is irregular but also volume.
EXAMPLE 03A19_Sample_by_sample_processing.csd
<CsoundSynthesizer>
<CsOptions>
-odac -m128
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr SimpleTest
iFac = p4 ;multiplier for each audio sample
aSinus poscil 0.1, 500
kIndx = 0
while kIndx < ksmps do
aSinus[kIndx] = aSinus[kIndx] * iFac + aSinus[kIndx]
kIndx += 1
od
out aSinus, aSinus
endin
instr PrintSampleIf
aRnd rnd31 1, 0, 1
kBlkCnt init 0
kSmpCnt init 0
kIndx = 0
while kIndx < ksmps do
if aRnd[kIndx] > 0.99 then
printf "Block = %2d, Sample = %4d, Value = %f\n", kSmpCnt, kBlkCnt, kSmpCnt, aRnd[kIndx]
endif
kIndx += 1
kSmpCnt += 1
od
kBlkCnt += 1
endin
instr PlaySampleIf
aRnd rnd31 1, 0, 1
aOut init 0
kBlkCnt init 0
kSmpCnt init 0
kIndx = 0
while kIndx < ksmps do
if aRnd[kIndx] > 0 && aRnd[kIndx] < 1/10000 then
aOut[kIndx] = aRnd[kIndx] * 10000
else
aOut[kIndx] = 0
endif
kIndx += 1
od
out aOut, aOut
endin
</CsInstruments>
<CsScore>
i "SimpleTest" 0 1 1
i "SimpleTest" 2 1 3
i "SimpleTest" 4 1 -1
i "PrintSampleIf" 6 .033
i "PlaySampleIf" 8 10
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
The output should contain these lines, generated by the "PrintSampleIf" instrument, showing that in block 40 there were two subsequent samples which fell under the condition:
Block = 2, Sample = 86, Value = 0.998916
Block = 7, Sample = 244, Value = 0.998233
Block = 19, Sample = 638, Value = 0.995197
Block = 27, Sample = 883, Value = 0.990801
Block = 34, Sample = 1106, Value = 0.997471
Block = 40, Sample = 1308, Value = 1.000000
Block = 40, Sample = 1309, Value = 0.998184
Block = 43, Sample = 1382, Value = 0.994353
At the end of chapter 03G an example is shown for a more practical use of sample-by-sample processing in Csound: to implement a digital filter as user defined opcode.
Hidden Initialization of k- and S-Variables
Any k-variable can be explicitly initialized by the init opcode, as has been shown above. But internally any variable, it be control rate (k), audio rate (a) or string (S), has an initial value. As this initialization can be hidden from the user, it can lead to unexpexted behaviour.
Explicit and implicit initialization
The first case is easy to understand, although some results may be unexpected. Any k-variable which is not explicitly initialized is set to zero as initial value.
EXAMPLE 03A20_Init_explcit_implicit.csd
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1
;explicit initialization
k_Exp init 10
S_Exp init "goodbye"
;implicit initialization
k_Imp linseg 10, 1, 0
S_Imp strcpyk "world"
;print out at init-time
prints "k_Exp -> %d\n", k_Exp
printf_i "S_Exp -> %s\n", 1, S_Exp
prints "k_Imp -> %d\n", k_Imp
printf_i "S_Imp -> %s\n", 1, S_Imp
endin
</CsInstruments>
<CsScore>
i 1 0 1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
This is the console output:
k_Exp -> 10
S_Exp -> goodbye
k_Imp -> 0
S_Imp -> world
The implicit output may be of some surprise. The variable k_Imp is not initilalized to 10, although 10 will be the first value during performance. And S_Imp carries the "world" already at initialization although the opcode name strcpyk may suggest something else. But as the manual page states: "strcpyk does the assignment both at initialization and performance time."
Order of initialization statements
What happens if there are two init statements, following each other? Usually the second one overwrites the first. But if a k-value is explicitely set via the init opcode, the implicit initialization will not take place.
EXAMPLE 03A21_Init_overwrite.csd
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1
;k-variables
k_var init 20
k_var linseg 10, 1, 0
;string variables
S_var init "goodbye"
S_var strcpyk "world"
;print out at init-time
prints "k_var -> %d\n", k_var
printf_i "S_var -> %s\n", 1, S_var
endin
</CsInstruments>
<CsScore>
i 1 0 1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
The output is:
k_var -> 20
S_var -> world
Both pairs of lines in the code look similar, but do something quite different. For k_var the line k_var linseg 10, 1, 0 will not initialize k_var to zero, as this happens only if no init value is assigned. The line S_var strcpyk "world" instead does an explicit initialization, and this initialization will overwrite the preceding one. If the lines were swapped, the result would be "goodbye" rather than "world".
Hidden initialization in k-rate if-clause
If-clauses can be either i-rate or k-rate. A k-rate if-clause initializes nevertheless. Reading the next example may suggest that the variable String is only initalized to "yes", because the if-condition will never become true. But regardless it is true or false, any k-rate if-clause initializes its expressions, in this case the String variable.
EXAMPLE 03A22_Init_hidden_in_if.csd
<CsoundSynthesizer>
<CsOptions>
-m128
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1
;a string to be copied at init- and performance-time
String strcpyk "yes!\n"
;print it at init-time
printf_i "INIT 1: %s", 1, String
;a copy assignment that will never become true during performance
kBla = 0
if kBla == 1 then
String strcpyk "no!\n"
endif
;nevertheless the string variable is initialized by it
printf_i "INIT 2: %s", 1, String
;during performance only "yes!" remains
printf "PERF %d: %s", timeinstk(), timeinstk(), String
;turn off after three k-cycles
if timeinstk() == 3 then
turnoff
endif
endin
</CsInstruments>
<CsScore>
i 1 0 1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Returns:
INIT 1: yes!
INIT 2: no!
PERF 1: yes!
PERF 2: yes!
PERF 3: yes!
If you want to skip the initialization at this point, you can use an igoto statement:
if kBla == 1 then
igoto skip
String strcpyk "no!\n"
skip:
endif
Hidden initialization via UDOs
A user may expect that a UDO will behave identical to a csound native opcode, but in terms of implicit initialization it is not the case. In the following example, we may expect that instrument 2 has the same output as instrument 1.
EXAMPLE 03A23_Init_hidden_in_udo.csd
<CsoundSynthesizer>
<CsOptions>
-m128
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
opcode RndInt, k, kk
kMin, kMax xin
kRnd random kMin, kMax+.999999
kRnd = int(kRnd)
xout kRnd
endop
instr 1 ;opcode
kBla init 10
kBla random 1, 2
prints "instr 1: kBla initialized to %d\n", i(kBla)
turnoff
endin
instr 2 ;udo has different effect at i-time
kBla init 10
kBla RndInt 1, 2
prints "instr 2: kBla initialized to %d\n", i(kBla)
turnoff
endin
instr 3 ;but the functional syntax makes it different
kBla init 10
kBla = RndInt(1, 2)
prints "instr 3: kBla initialized to %d\n", i(kBla)
turnoff
endin
</CsInstruments>
<CsScore>
i 1 0 .1
i 2 + .
i 3 + .
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
But the output is:
instr 1: kBla initialized to 10
instr 2: kBla initialized to 0
instr 3: kBla initialized to 10
The reason that instrument 2 does implicit initialization of kBla is written in the manual page for xin / xout: "These opcodes actually run only at i-time." In this case, kBla is initialized to zero, because the kRnd variable inside the UDO is implicitly zero at init-time.
Instrument 3, on the other hand, uses the '=' operator. It works as other native opcodes: if a k-variable has an explicit init value, it does not initialize again.
The examples about hidden (implicit) initialization may look somehow sophisticated and far from normal usage. But this is not the case. As users we may think: "I perform a line from 10 to 0 in 1 second, and i write this in the variable kLine. So i(kLine) is 10." It is not, and if you send this value at init-time to another instrument, your program will give wrong output.
When to Use i- or k- Rate
When you code on your Csound instrument, you may sometimes wonder whether you shall use an i-rate or a k-rate opcode. From what is said, the general answer is clear: Use i-rate if something has to be done only once, or in a somehow punctual manner. Use k-rate if something has to be done continuously, or if you must regard what happens during the performance.
- You would not get any other result if you set p3 to 1 or any other value, as nothing is done here except initialization.^
- For the physical result which comes out of the loudspeakers or headphones, the variation is the variation of air pressure.^
- 44100 samples per second^
- These are by the way the times which Csound reports if you ask for the control cycles. The first control cycle in this example (sr=44100, ksmps=10) would be reported as 0.00027 seconds, not as 0.00000 seconds.^
- As Richard Boulanger explains, in early Csound a line starting with 'c' was a comment line. So it was not possible to abbreviate control variables as cAnything (http://csound.1045644.n5.nabble.com/OT-why-is-control-rate-called-kontrol-rate-td5720858.html#a5720866). ^
- As the k-rate is directly depending on sample rate (sr) and ksmps (kr = sr/ksmps), it is probably the best style to specify sr and ksmps in the header, but not kr. ^
- This must not be confused with a 'real' k-loop where inside one single k-cycle a loop is performed. See chapter 03C (section Loops) for examples.^
- The value is 3110 instead of 3100 because it has already been incremented by 10.^
- See the manual page for printk, printk2, printks, printf to know more about the differences.^
- If you want to know the number in an instrument, use the nstrnum opcode. ^
- See the following section 03B about the variable types for more on this subject.^
LOCAL AND GLOBAL VARIABLES
Variable Types
In Csound, there are several types of variables. It is important to understand the differences between these types. There are
- initialization variables, which are updated at each initialization pass, i.e. at the beginning of each note or score event. They start with the character i. To this group count also the score parameter fields, which always starts with a p, followed by any number: p1 refers to the first parameter field in the score, p2 to the second one, and so on.
- control variables, which are updated at each control cycle during the performance of an instrument. They start with the character k.
- audio variables, which are also updated at each control cycle, but instead of a single number (like control variables) they consist of a vector (a collection of numbers), having in this way one number for each sample. They start with the character a.
- string variables, which are updated either at i-time or at k-time (depending on the opcode which produces a string). They start with the character S.
Except these four standard types, there are two other variable types which are used for spectral processing:
- f-variables are used for the streaming phase vocoder opcodes (all starting with the characters pvs), which are very important for doing realtime FFT (Fast Fourier Transform) in Csound. They are updated at k-time, but their values depend also on the FFT parameters like frame size and overlap.
- w-variables are used in some older spectral processing opcodes.
The following example exemplifies all the variable types (except the w-type):
EXAMPLE 03B01_Variable_types.csd
<CsoundSynthesizer>
<CsOptions>
--env:SSDIR+=../SourceMaterials -o dac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
0dbfs = 1
nchnls = 2
seed 0; random seed each time different
instr 1; i-time variables
iVar1 = p2; second parameter in the score
iVar2 random 0, 10; random value between 0 and 10
iVar = iVar1 + iVar2; do any math at i-rate
print iVar1, iVar2, iVar
endin
instr 2; k-time variables
kVar1 line 0, p3, 10; moves from 0 to 10 in p3
kVar2 random 0, 10; new random value each control-cycle
kVar = kVar1 + kVar2; do any math at k-rate
; --- print each 0.1 seconds
printks "kVar1 = %.3f, kVar2 = %.3f, kVar = %.3f%n", 0.1, kVar1, kVar2, kVar
endin
instr 3; a-variables
aVar1 poscil .2, 400; first audio signal: sine
aVar2 rand 1; second audio signal: noise
aVar3 butbp aVar2, 1200, 12; third audio signal: noise filtered
aVar = aVar1 + aVar3; audio variables can also be added
outs aVar, aVar; write to sound card
endin
instr 4; S-variables
iMyVar random 0, 10; one random value per note
kMyVar random 0, 10; one random value per each control-cycle
;S-variable updated just at init-time
SMyVar1 sprintf "This string is updated just at init-time: kMyVar = %d\n", iMyVar
printf_i "%s", 1, SMyVar1
;S-variable updates at each control-cycle
printks "This string is updated at k-time: kMyVar = %.3f\n", .1, kMyVar
endin
instr 5; f-variables
aSig rand .2; audio signal (noise)
; f-signal by FFT-analyzing the audio-signal
fSig1 pvsanal aSig, 1024, 256, 1024, 1
; second f-signal (spectral bandpass filter)
fSig2 pvsbandp fSig1, 350, 400, 400, 450
aOut pvsynth fSig2; change back to audio signal
outs aOut*20, aOut*20
endin
</CsInstruments>
<CsScore>
; p1 p2 p3
i 1 0 0.1
i 1 0.1 0.1
i 2 1 1
i 3 2 1
i 4 3 1
i 5 4 1
</CsScore>
</CsoundSynthesizer>
You can think of variables as named connectors between opcodes. You can connect the output from an opcode to the input of another. The type of connector (audio, control, etc.) is determined by the first letter of its name.
For a more detailed discussion, see the article An overview Of Csound Variable Types by Andrés Cabrera in the Csound Journal, and the page about Types, Constants and Variables in the Canonical Csound Manual.
Local Scope
The scope of these variables is usually the instrument in which they are defined. They are local variables. In the following example, the variables in instrument 1 and instrument 2 have the same names, but different values.
EXAMPLE 03B02_Local_scope.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 4410; very high because of printing
nchnls = 2
0dbfs = 1
instr 1
;i-variable
iMyVar init 0
iMyVar = iMyVar + 1
print iMyVar
;k-variable
kMyVar init 0
kMyVar = kMyVar + 1
printk 0, kMyVar
;a-variable
aMyVar oscils .2, 400, 0
outs aMyVar, aMyVar
;S-variable updated just at init-time
SMyVar1 sprintf "This string is updated just at init-time:
kMyVar = %d\n", i(kMyVar)
printf "%s", kMyVar, SMyVar1
;S-variable updated at each control-cycle
SMyVar2 sprintfk "This string is updated at k-time:
kMyVar = %d\n", kMyVar
printf "%s", kMyVar, SMyVar2
endin
instr 2
;i-variable
iMyVar init 100
iMyVar = iMyVar + 1
print iMyVar
;k-variable
kMyVar init 100
kMyVar = kMyVar + 1
printk 0, kMyVar
;a-variable
aMyVar oscils .3, 600, 0
outs aMyVar, aMyVar
;S-variable updated just at init-time
SMyVar1 sprintf "This string is updated just at init-time:
kMyVar = %d\n", i(kMyVar)
printf "%s", kMyVar, SMyVar1
;S-variable updated at each control-cycle
SMyVar2 sprintfk "This string is updated at k-time:
kMyVar = %d\n", kMyVar
printf "%s", kMyVar, SMyVar2
endin
</CsInstruments>
<CsScore>
i 1 0 .3
i 2 1 .3
</CsScore>
</CsoundSynthesizer>
This is the output (first the output at init-time by the print opcode, then at each k-cycle the output of printk and the two printf opcodes):
new alloc for instr 1:
instr 1: iMyVar = 1.000
i 1 time 0.10000: 1.00000
This string is updated just at init-time: kMyVar = 0
This string is updated at k-time: kMyVar = 1
i 1 time 0.20000: 2.00000
This string is updated just at init-time: kMyVar = 0
This string is updated at k-time: kMyVar = 2
i 1 time 0.30000: 3.00000
This string is updated just at init-time: kMyVar = 0
This string is updated at k-time: kMyVar = 3
B 0.000 .. 1.000 T 1.000 TT 1.000 M: 0.20000 0.20000
new alloc for instr 2:
instr 2: iMyVar = 101.000
i 2 time 1.10000: 101.00000
This string is updated just at init-time: kMyVar = 100
This string is updated at k-time: kMyVar = 101
i 2 time 1.20000: 102.00000
This string is updated just at init-time: kMyVar = 100
This string is updated at k-time: kMyVar = 102
i 2 time 1.30000: 103.00000
This string is updated just at init-time: kMyVar = 100
This string is updated at k-time: kMyVar = 103
B 1.000 .. 1.300 T 1.300 TT 1.300 M: 0.29998 0.29998
Global Scope
If you need variables which are recognized beyond the scope of an instrument, you must define them as global. This is done by prefixing the character g before the types i, k, a or S. See the following example:
EXAMPLE 03B03_Global_scope.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 4410; very high because of printing
nchnls = 2
0dbfs = 1
;global scalar variables should be inititalized in the header
giMyVar init 0
gkMyVar init 0
instr 1
;global i-variable
giMyVar = giMyVar + 1
print giMyVar
;global k-variable
gkMyVar = gkMyVar + 1
printk 0, gkMyVar
;global S-variable updated just at init-time
gSMyVar1 sprintf "This string is updated just at init-time:
gkMyVar = %d\n", i(gkMyVar)
printf "%s", gkMyVar, gSMyVar1
;global S-variable updated at each control-cycle
gSMyVar2 sprintfk "This string is updated at k-time:
gkMyVar = %d\n", gkMyVar
printf "%s", gkMyVar, gSMyVar2
endin
instr 2
;global i-variable, gets value from instr 1
giMyVar = giMyVar + 1
print giMyVar
;global k-variable, gets value from instr 1
gkMyVar = gkMyVar + 1
printk 0, gkMyVar
;global S-variable updated just at init-time, gets value from instr 1
printf "Instr 1 tells: '%s'\n", gkMyVar, gSMyVar1
;global S-variable updated at each control-cycle, gets value from instr 1
printf "Instr 1 tells: '%s'\n\n", gkMyVar, gSMyVar2
endin
</CsInstruments>
<CsScore>
i 1 0 .3
i 2 0 .3
</CsScore>
</CsoundSynthesizer>
The output shows the global scope, as instrument 2 uses the values which have been changed by instrument 1 in the same control cycle:new alloc for instr 1:
instr 1: giMyVar = 1.000
new alloc for instr 2:
instr 2: giMyVar = 2.000
i 1 time 0.10000: 1.00000
This string is updated just at init-time: gkMyVar = 0
This string is updated at k-time: gkMyVar = 1
i 2 time 0.10000: 2.00000
Instr 1 tells: 'This string is updated just at init-time: gkMyVar = 0'
Instr 1 tells: 'This string is updated at k-time: gkMyVar = 1'
i 1 time 0.20000: 3.00000
This string is updated just at init-time: gkMyVar = 0
This string is updated at k-time: gkMyVar = 3
i 2 time 0.20000: 4.00000
Instr 1 tells: 'This string is updated just at init-time: gkMyVar = 0'
Instr 1 tells: 'This string is updated at k-time: gkMyVar = 3'
i 1 time 0.30000: 5.00000
This string is updated just at init-time: gkMyVar = 0
This string is updated at k-time: gkMyVar = 5
i 2 time 0.30000: 6.00000
Instr 1 tells: 'This string is updated just at init-time: gkMyVar = 0'
Instr 1 tells: 'This string is updated at k-time: gkMyVar = 5'
How To Work With Global Audio Variables
Some special considerations must be taken if you work with global audio variables. Actually, Csound behaves basically the same whether you work with a local or a global audio variable. But usually you work with global audio variables if you want to add several audio signals to a global signal, and that makes a difference.
The next few examples are going into a bit more detail. If you just want to see the result (= global audio usually must be cleared), you can skip the next examples and just go to the last one of this section.
It should be understood first that a global audio variable is treated the same by Csound if it is applied like a local audio signal:
EXAMPLE 03B04_Global_audio_intro.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1; produces a 400 Hz sine
gaSig oscils .1, 400, 0
endin
instr 2; outputs gaSig
outs gaSig, gaSig
endin
</CsInstruments>
<CsScore>
i 1 0 3
i 2 0 3
</CsScore>
</CsoundSynthesizer>
Of course there is no need to use a global variable in this case. If you do it, you risk your audio will be overwritten by an instrument with a higher number using the same variable name. In the following example, you will just hear a 600 Hz sine tone, because the 400 Hz sine of instrument 1 is overwritten by the 600 Hz sine of instrument 2:
EXAMPLE 03B05_Global_audio_overwritten.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1; produces a 400 Hz sine
gaSig oscils .1, 400, 0
endin
instr 2; overwrites gaSig with 600 Hz sine
gaSig oscils .1, 600, 0
endin
instr 3; outputs gaSig
outs gaSig, gaSig
endin
</CsInstruments>
<CsScore>
i 1 0 3
i 2 0 3
i 3 0 3
</CsScore>
</CsoundSynthesizer>
In general, you will use a global audio variable like a bus to which several local audio signal can be added. It's this addition of a global audio signal to its previous state which can cause some trouble. Let's first see a simple example of a control signal to understand what is happening:
EXAMPLE 03B06_Global_audio_added.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 4410; very high because of printing
nchnls = 2
0dbfs = 1
instr 1
kSum init 0; sum is zero at init pass
kAdd = 1; control signal to add
kSum = kSum + kAdd; new sum in each k-cycle
printk 0, kSum; print the sum
endin
</CsInstruments>
<CsScore>
i 1 0 1
</CsScore>
</CsoundSynthesizer>
In this case, the "sum bus" kSum increases at each control cycle by 1, because it adds the kAdd signal (which is always 1) in each k-pass to its previous state. It is no different if this is done by a local k-signal, like here, or by a global k-signal, like in the next example:
EXAMPLE 03B07_Global_control_added.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 4410; very high because of printing
nchnls = 2
0dbfs = 1
gkSum init 0; sum is zero at init
instr 1
gkAdd = 1; control signal to add
endin
instr 2
gkSum = gkSum + gkAdd; new sum in each k-cycle
printk 0, gkSum; print the sum
endin
</CsInstruments>
<CsScore>
i 1 0 1
i 2 0 1
</CsScore>
</CsoundSynthesizer>
What happens when working with audio signals instead of control signals in this way, repeatedly adding a signal to its previous state? Audio signals in Csound are a collection of numbers (a vector). The size of this vector is given by the ksmps constant. If your sample rate is 44100, and ksmps=100, you will calculate 441 times in one second a vector which consists of 100 numbers, indicating the amplitude of each sample.
So, if you add an audio signal to its previous state, different things can happen, depending on the vector's present and previous states. If both previous and present states (with ksmps=9) are [0 0.1 0.2 0.1 0 -0.1 -0.2 -0.1 0] you will get a signal which is twice as strong: [0 0.2 0.4 0.2 0 -0.2 -0.4 -0.2 0]. But if the present state is opposite [0 -0.1 -0.2 -0.1 0 0.1 0.2 0.1 0], you will only get zeros when you add them. This is shown in the next example with a local audio variable, and then in the following example with a global audio variable.
EXAMPLE 03B08_Local_audio_add.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 4410; very high because of printing
;(change to 441 to see the difference)
nchnls = 2
0dbfs = 1
instr 1
;initialize a general audio variable
aSum init 0
;produce a sine signal (change frequency to 401 to see the difference)
aAdd oscils .1, 400, 0
;add it to the general audio (= the previous vector)
aSum = aSum + aAdd
kmax max_k aSum, 1, 1; calculate maximum
printk 0, kmax; print it out
outs aSum, aSum
endin
</CsInstruments>
<CsScore>
i 1 0 1
</CsScore>
</CsoundSynthesizer>
prints:
i 1 time 0.10000: 0.10000
i 1 time 0.20000: 0.20000
i 1 time 0.30000: 0.30000
i 1 time 0.40000: 0.40000
i 1 time 0.50000: 0.50000
i 1 time 0.60000: 0.60000
i 1 time 0.70000: 0.70000
i 1 time 0.80000: 0.79999
i 1 time 0.90000: 0.89999
i 1 time 1.00000: 0.99999
EXAMPLE 03B09_Global_audio_add.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 4410; very high because of printing
;(change to 441 to see the difference)
nchnls = 2
0dbfs = 1
;initialize a general audio variable
gaSum init 0
instr 1
;produce a sine signal (change frequency to 401 to see the difference)
aAdd oscils .1, 400, 0
;add it to the general audio (= the previous vector)
gaSum = gaSum + aAdd
endin
instr 2
kmax max_k gaSum, 1, 1; calculate maximum
printk 0, kmax; print it out
outs gaSum, gaSum
endin
</CsInstruments>
<CsScore>
i 1 0 1
i 2 0 1
</CsScore>
</CsoundSynthesizer>
In both cases, you get a signal which increases each 1/10 second, because you have 10 control cycles per second (ksmps=4410), and the frequency of 400 Hz can be evenly divided by this. If you change the ksmps value to 441, you will get a signal which increases much faster and is out of range after 1/10 second. If you change the frequency to 401 Hz, you will get a signal which increases first, and then decreases, because each audio vector has 40.1 cycles of the sine wave. So the phases are shifting; first getting stronger and then weaker. If you change the frequency to 10 Hz, and then to 15 Hz (at ksmps=44100), you cannot hear anything, but if you render to file, you can see the whole process of either enforcing or erasing quite clear:
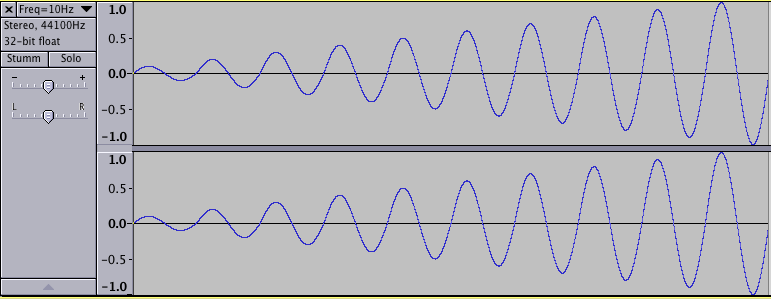
Self-reinforcing global audio signal on account of its state in one control cycle being the same as in the previous one

So the result of all is: If you work with global audio variables in a way that you add several local audio signals to a global audio variable (which works like a bus), you must clear this global bus at each control cycle. As in Csound all the instruments are calculated in ascending order, it should be done either at the beginning of the first, or at the end of the last instrument. Perhaps it is the best idea to declare all global audio variables in the orchestra header first, and then clear them in an "always on" instrument with the highest number of all the instruments used. This is an example of a typical situation:
EXAMPLE 03B10_Global_with_clear.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
;initialize the global audio variables
gaBusL init 0
gaBusR init 0
;make the seed for random values each time different
seed 0
instr 1; produces short signals
loop:
iDur random .3, 1.5
timout 0, iDur, makenote
reinit loop
makenote:
iFreq random 300, 1000
iVol random -12, -3; dB
iPan random 0, 1; random panning for each signal
aSin oscil3 ampdb(iVol), iFreq, 1
aEnv transeg 1, iDur, -10, 0; env in a-rate is cleaner
aAdd = aSin * aEnv
aL, aR pan2 aAdd, iPan
gaBusL = gaBusL + aL; add to the global audio signals
gaBusR = gaBusR + aR
endin
instr 2; produces short filtered noise signals (4 partials)
loop:
iDur random .1, .7
timout 0, iDur, makenote
reinit loop
makenote:
iFreq random 100, 500
iVol random -24, -12; dB
iPan random 0, 1
aNois rand ampdb(iVol)
aFilt reson aNois, iFreq, iFreq/10
aRes balance aFilt, aNois
aEnv transeg 1, iDur, -10, 0
aAdd = aRes * aEnv
aL, aR pan2 aAdd, iPan
gaBusL = gaBusL + aL; add to the global audio signals
gaBusR = gaBusR + aR
endin
instr 3; reverb of gaBus and output
aL, aR freeverb gaBusL, gaBusR, .8, .5
outs aL, aR
endin
instr 100; clear global audios at the end
clear gaBusL, gaBusR
endin
</CsInstruments>
<CsScore>
f 1 0 1024 10 1 .5 .3 .1
i 1 0 20
i 2 0 20
i 3 0 20
i 100 0 20
</CsScore>
</CsoundSynthesizer>
The chn Opcodes For Global Variables
Instead of using the traditional g-variables for any values or signals which are to transfer between several instruments, it is also possible to use the chn opcodes. An i-, k-, a- or S-value or signal can be set by chnset and received by chnget. One advantage is to have strings as names, so that you can choose intuitive names.
For audio variables, instead of performing an addition, you can use the chnmix opcode. For clearing an audio variable, the chnclear opcode can be used.
EXAMPLE 03B11_Chn_demo.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1; send i-values
chnset 1, "sio"
chnset -1, "non"
endin
instr 2; send k-values
kfreq randomi 100, 300, 1
chnset kfreq, "cntrfreq"
kbw = kfreq/10
chnset kbw, "bandw"
endin
instr 3; send a-values
anois rand .1
chnset anois, "noise"
loop:
idur random .3, 1.5
timout 0, idur, do
reinit loop
do:
ifreq random 400, 1200
iamp random .1, .3
asig oscils iamp, ifreq, 0
aenv transeg 1, idur, -10, 0
asine = asig * aenv
chnset asine, "sine"
endin
instr 11; receive some chn values and send again
ival1 chnget "sio"
ival2 chnget "non"
print ival1, ival2
kcntfreq chnget "cntrfreq"
kbandw chnget "bandw"
anoise chnget "noise"
afilt reson anoise, kcntfreq, kbandw
afilt balance afilt, anoise
chnset afilt, "filtered"
endin
instr 12; mix the two audio signals
amix1 chnget "sine"
amix2 chnget "filtered"
chnmix amix1, "mix"
chnmix amix2, "mix"
endin
instr 20; receive and reverb
amix chnget "mix"
aL, aR freeverb amix, amix, .8, .5
outs aL, aR
endin
instr 100; clear
chnclear "mix"
endin
</CsInstruments>
<CsScore>
i 1 0 20
i 2 0 20
i 3 0 20
i 11 0 20
i 12 0 20
i 20 0 20
i 100 0 20
</CsScore>
</CsoundSynthesizer>
Csound: CONTROLSTRUCTURES
CONTROL STRUCTURES
In a way, control structures are the core of a programming language. The fundamental element in each language is the conditional if branch. Actually all other control structures like for-, until- or while-loops can be traced back to if-statements.
So, Csound provides mainly the if-statement; either in the usual if-then-else form, or in the older way of an if-goto statement. These will be covered first. Though all necessary loops can be built just by if-statements, Csound's while, until and loop facility offer a more comfortable way of performing loops. They will be introduced later, in the Loop and the While / Until section of this chapter. Finally, time loops are shown, which are particulary important in audio programming languages.
If i-Time Then Not k-Time!
The fundamental difference in Csound between i-time and k-time which has been explained in chapter 03A, must be regarded very carefully when you work with control structures. If you make a conditional branch at i-time, the condition will be tested just once for each note, at the initialization pass. If you make a conditional branch at k-time, the condition will be tested again and again in each control-cycle.
For instance, if you test a soundfile whether it is mono or stereo, this is done at init-time. If you test an amplitude value to be below a certain threshold, it is done at performance time (k-time). If you get user-input by a scroll number, this is also a k-value, so you need a k-condition.
Thus, all if and loop opcodes have an "i" and a "k" descendant. In the next few sections, a general introduction into the different control tools is given, followed by examples both at i-time and at k-time for each tool.
If - then - [elseif - then -] else
The use of the if-then-else statement is very similar to other programming languages. Note that in Csound, "then" must be written in the same line as "if" and the expression to be tested, and that you must close the if-block with an "endif" statement on a new line:
if <condition> then ... else ... endif
It is also possible to have no "else" statement:
if <condition> then ... endif
Or you can have one or more "elseif-then" statements in between:
if <condition1> then ... elseif <condition2> then ... else ... endif
If statements can also be nested. Each level must be closed with an "endif". This is an example with three levels:
if <condition1> then; first condition opened if <condition2> then; second condition openend if <condition3> then; third condition openend ... else ... endif; third condition closed elseif <condition2a> then ... endif; second condition closed else ... endif; first condition closed
i-Rate Examples
A typical problem in Csound: You have either mono or stereo files, and want to read both with a stereo output. For the real stereo ones that means: use soundin (diskin / diskin2) with two output arguments. For the mono ones it means: use soundin / diskin / diskin2 with one output argument, and throw it to both output channels:
EXAMPLE 03C01_IfThen_i.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1
Sfile = "/my/file.wav" ;your soundfile path here
ifilchnls filenchnls Sfile
if ifilchnls == 1 then ;mono
aL soundin Sfile
aR = aL
else ;stereo
aL, aR soundin Sfile
endif
outs aL, aR
endin
</CsInstruments>
<CsScore>
i 1 0 5
</CsScore>
</CsoundSynthesizer>
If you use CsoundQt, you can browse in the widget panel for the soundfile. See the corresponding example in the CsoundQt Example menu.
k-Rate Examples
The following example establishes a moving gate between 0 and 1. If the gate is above 0.5, the gate opens and you hear a tone. If the gate is equal or below 0.5, the gate closes, and you hear nothing.
EXAMPLE 03C02_IfThen_k.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0; random values each time different
giTone ftgen 0, 0, 2^10, 10, 1, .5, .3, .1
instr 1
; move between 0 and 1 (3 new values per second)
kGate randomi 0, 1, 3
; move between 300 and 800 hz (1 new value per sec)
kFreq randomi 300, 800, 1
; move between -12 and 0 dB (5 new values per sec)
kdB randomi -12, 0, 5
aSig oscil3 1, kFreq, giTone
kVol init 0
if kGate > 0.5 then; if kGate is larger than 0.5
kVol = ampdb(kdB); open gate
else
kVol = 0; otherwise close gate
endif
kVol port kVol, .02; smooth volume curve to avoid clicks
aOut = aSig * kVol
outs aOut, aOut
endin
</CsInstruments>
<CsScore>
i 1 0 30
</CsScore>
</CsoundSynthesizer>
Short Form: (a v b ? x : y)
If you need an if-statement to give a value to an (i- or k-) variable, you can also use a traditional short form in parentheses: (a v b ? x : y).1 It asks whether the condition a or b is true. If a, the value is set to x; if b, to y. For instance, the last example could be written in this way:
EXAMPLE 03C03_IfThen_short_form.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0
giTone ftgen 0, 0, 2^10, 10, 1, .5, .3, .1
instr 1
kGate randomi 0, 1, 3; moves between 0 and 1 (3 new values per second)
kFreq randomi 300, 800, 1; moves between 300 and 800 hz
;(1 new value per sec)
kdB randomi -12, 0, 5; moves between -12 and 0 dB
;(5 new values per sec)
aSig oscil3 1, kFreq, giTone
kVol init 0
kVol = (kGate > 0.5 ? ampdb(kdB) : 0); short form of condition
kVol port kVol, .02; smooth volume curve to avoid clicks
aOut = aSig * kVol
outs aOut, aOut
endin
</CsInstruments>
<CsScore>
i 1 0 20
</CsScore>
</CsoundSynthesizer>
If - goto
An older way of performing a conditional branch - but still useful in certain cases - is an "if" statement which is not followed by a "then", but by a label name. The "else" construction follows (or doesn't follow) in the next line. Like the if-then-else statement, the if-goto works either at i-time or at k-time. You should declare the type by either using igoto or kgoto. Usually you need an additional igoto/kgoto statement for omitting the "else" block if the first condition is true. This is the general syntax:
i-time
if <condition> igoto this; same as if-then igoto that; same as else this: ;the label "this" ... ... igoto continue ;skip the "that" block that: ; ... and the label "that" must be found ... continue: ;go on after the conditional branch ...
k-time
if <condition> kgoto this; same as if-then kgoto that; same as else this: ;the label "this" ... ... kgoto continue ;skip the "that" block that: ; ... and the label "that" must be found ... continue: ;go on after the conditional branch ...
i-Rate Examples
This is the same example as above in the if-then-else syntax for a branch depending on a mono or stereo file. If you just want to know whether a file is mono or stereo, you can use the "pure" if-igoto statement:
EXAMPLE 03C04_IfGoto_i.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1
Sfile = "/Joachim/Materialien/SamplesKlangbearbeitung/Kontrabass.aif"
ifilchnls filenchnls Sfile
if ifilchnls == 1 igoto mono; condition if true
igoto stereo; else condition
mono:
prints "The file is mono!%n"
igoto continue
stereo:
prints "The file is stereo!%n"
continue:
endin
</CsInstruments>
<CsScore>
i 1 0 0
</CsScore>
</CsoundSynthesizer>
But if you want to play the file, you must also use a k-rate if-kgoto, because, not only do you have an event at i-time (initializing the soundin opcode) but also at k-time (producing an audio signal). So the code in this case is much more cumbersome, or obfuscated, than the previous if-then-else example.
EXAMPLE 03C05_IfGoto_ik.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1
Sfile = "my/file.wav"
ifilchnls filenchnls Sfile
if ifilchnls == 1 kgoto mono
kgoto stereo
if ifilchnls == 1 igoto mono; condition if true
igoto stereo; else condition
mono:
aL soundin Sfile
aR = aL
igoto continue
kgoto continue
stereo:
aL, aR soundin Sfile
continue:
outs aL, aR
endin
</CsInstruments>
<CsScore>
i 1 0 5
</CsScore>
</CsoundSynthesizer>
k-Rate Examples
This is the same example as above (03C02) in the if-then-else syntax for a moving gate between 0 and 1:
EXAMPLE 03C06_IfGoto_k.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0
giTone ftgen 0, 0, 2^10, 10, 1, .5, .3, .1
instr 1
kGate randomi 0, 1, 3; moves between 0 and 1 (3 new values per second)
kFreq randomi 300, 800, 1; moves between 300 and 800 hz
;(1 new value per sec)
kdB randomi -12, 0, 5; moves between -12 and 0 dB
;(5 new values per sec)
aSig oscil3 1, kFreq, giTone
kVol init 0
if kGate > 0.5 kgoto open; if condition is true
kgoto close; "else" condition
open:
kVol = ampdb(kdB)
kgoto continue
close:
kVol = 0
continue:
kVol port kVol, .02; smooth volume curve to avoid clicks
aOut = aSig * kVol
outs aOut, aOut
endin
</CsInstruments>
<CsScore>
i 1 0 30
</CsScore>
</CsoundSynthesizer>
Loops
Loops can be built either at i-time or at k-time just with the "if" facility. The following example shows an i-rate and a k-rate loop created using the if-i/kgoto facility:
EXAMPLE 03C07_Loops_with_if.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Joachim Heintz
instr 1 ;i-time loop: counts from 1 until 10 has been reached
icount = 1
count:
print icount
icount = icount + 1
if icount < 11 igoto count
prints "i-END!%n"
endin
instr 2 ;k-rate loop: counts in the 100th k-cycle from 1 to 11
kcount init 0
ktimek timeinstk ;counts k-cycle from the start of this instrument
if ktimek == 100 kgoto loop
kgoto noloop
loop:
printks "k-cycle %d reached!%n", 0, ktimek
kcount = kcount + 1
printk2 kcount
if kcount < 11 kgoto loop
printks "k-END!%n", 0
noloop:
endin
</CsInstruments>
<CsScore>
i 1 0 0
i 2 0 1
</CsScore>
</CsoundSynthesizer>
But Csound offers a slightly simpler syntax for this kind of i-rate or k-rate loops. There are four variants of the loop opcode. All four refer to a label as the starting point of the loop, an index variable as a counter, an increment or decrement, and finally a reference value (maximum or minimum) as comparision:
- loop_lt counts upwards and looks if the index variable is lower than the reference value;
- loop_le also counts upwards and looks if the index is lower than or equal to the reference value;
- loop_gt counts downwards and looks if the index is greater than the reference value;
- loop_ge also counts downwards and looks if the index is greater than or equal to the reference value.
As always, all four opcodes can be applied either at i-time or at k-time. Here are some examples, first for i-time loops, and then for k-time loops.
i-Rate Examples
The following .csd provides a simple example for all four loop opcodes:
EXAMPLE 03C08_Loop_opcodes_i.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Joachim Heintz
instr 1 ;loop_lt: counts from 1 upwards and checks if < 10
icount = 1
loop:
print icount
loop_lt icount, 1, 10, loop
prints "Instr 1 terminated!%n"
endin
instr 2 ;loop_le: counts from 1 upwards and checks if <= 10
icount = 1
loop:
print icount
loop_le icount, 1, 10, loop
prints "Instr 2 terminated!%n"
endin
instr 3 ;loop_gt: counts from 10 downwards and checks if > 0
icount = 10
loop:
print icount
loop_gt icount, 1, 0, loop
prints "Instr 3 terminated!%n"
endin
instr 4 ;loop_ge: counts from 10 downwards and checks if >= 0
icount = 10
loop:
print icount
loop_ge icount, 1, 0, loop
prints "Instr 4 terminated!%n"
endin
</CsInstruments>
<CsScore>
i 1 0 0
i 2 0 0
i 3 0 0
i 4 0 0
</CsScore>
</CsoundSynthesizer>
The next example produces a random string of 10 characters and prints it out:
EXAMPLE 03C09_Random_string.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Joachim Heintz
instr 1
icount = 0
Sname = ""; starts with an empty string
loop:
ichar random 65, 90.999
Schar sprintf "%c", int(ichar); new character
Sname strcat Sname, Schar; append to Sname
loop_lt icount, 1, 10, loop; loop construction
printf_i "My name is '%s'!\n", 1, Sname; print result
endin
</CsInstruments>
<CsScore>
; call instr 1 ten times
r 10
i 1 0 0
</CsScore>
</CsoundSynthesizer>
You can also use an i-rate loop to fill a function table (= buffer) with any kind of values. This table can then be read, or manipulated and then be read again. In the next example, a function table with 20 positions (indices) is filled with random integers between 0 and 10 by instrument 1. Nearly the same loop construction is used afterwards to read these values by instrument 2.
EXAMPLE 03C10_Random_ftable_fill.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Joachim Heintz
giTable ftgen 0, 0, -20, -2, 0; empty function table with 20 points
seed 0; each time different seed
instr 1 ; writes in the table
icount = 0
loop:
ival random 0, 10.999 ;random value
; --- write in giTable at first, second, third ... position
tableiw int(ival), icount, giTable
loop_lt icount, 1, 20, loop; loop construction
endin
instr 2; reads from the table
icount = 0
loop:
; --- read from giTable at first, second, third ... position
ival tablei icount, giTable
print ival; prints the content
loop_lt icount, 1, 20, loop; loop construction
endin
</CsInstruments>
<CsScore>
i 1 0 0
i 2 0 0
</CsScore>
</CsoundSynthesizer>
k-Rate Examples
The next example performs a loop at k-time. Once per second, every value of an existing function table is changed by a random deviation of 10%. Though there are some vectorial opcodes for this task (and in Csound 6 probably array), it can also be done by a k-rate loop like the one shown here:
EXAMPLE 03C11_Table_random_dev.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 441
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 256, 10, 1; sine wave
seed 0; each time different seed
instr 1
ktiminstk timeinstk ;time in control-cycles
kcount init 1
if ktiminstk == kcount * kr then; once per second table values manipulation:
kndx = 0
loop:
krand random -.1, .1;random factor for deviations
kval table kndx, giSine; read old value
knewval = kval + (kval * krand); calculate new value
tablew knewval, kndx, giSine; write new value
loop_lt kndx, 1, 256, loop; loop construction
kcount = kcount + 1; increase counter
endif
asig poscil .2, 400, giSine
outs asig, asig
endin
</CsInstruments>
<CsScore>
i 1 0 10
</CsScore>
</CsoundSynthesizer>
While / Until
Since the release of Csound 6, it has been possible to write loops in a manner similar to that used by many other programming languages, using the keywords while or until. The general syntax is:2
while <condition> do ... od until <condition> do ... od
The body of the while loop will be performed again and again, as long as <condition> is true. The body of the until loop will be performed, as long as <condition> is false (not true). This is a simple example at i-rate:
EXAMPLE 03C12_while_until_i-rate.csd
<CsoundSynthesizer> <CsOptions> -nm0 </CsOptions> <CsInstruments> ksmps = 32 instr 1 iCounter = 0 while iCounter < 5 do print iCounter iCounter += 1 od prints "\n" endin instr 2 iCounter = 0 until iCounter >= 5 do print iCounter iCounter += 1 od endin </CsInstruments> <CsScore> i 1 0 .1 i 2 .1 .1 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
Prints:
instr 1: iprint = 0.000
instr 1: iprint = 1.000
instr 1: iprint = 2.000
instr 1: iprint = 3.000
instr 1: iprint = 4.000
instr 2: iprint = 0.000
instr 2: iprint = 1.000
instr 2: iprint = 2.000
instr 2: iprint = 3.000
instr 2: iprint = 4.000
The most important thing in using the while/until loop is to increment the variable you are using in the loop (here: iCounter). This is done by the statement
iCounter += 1
which is equivalent to the "old" way of writing as
iCounter = iCounter + 1
If you miss this increment, Csound will perform an endless loop, and you will have to terminate it by the operating system.
The next example shows a similar process at k-rate. It uses a while loop to print the values of an array, and also set new values. As this procedure is repeated in each control cycle, the instrument is being turned off after the third cycle.
EXAMPLE 03C13_while_until_k-rate.csd
<CsoundSynthesizer>
<CsOptions>
-nm0
</CsOptions>
<CsInstruments>
ksmps = 32
;create and fill an array
gkArray[] fillarray 1, 2, 3, 4, 5
instr 1
;count performance cycles and print it
kCycle timeinstk
printks "kCycle = %d\n", 0, kCycle
;set index to zero
kIndex = 0
;perform the loop
while kIndex < lenarray(gkArray) do
;print array value
printf " gkArray[%d] = %d\n", kIndex+1, kIndex, gkArray[kIndex]
;square array value
gkArray[kIndex] = gkArray[kIndex] * gkArray[kIndex]
;increment index
kIndex += 1
od
;stop after third control cycle
if kCycle == 3 then
turnoff
endif
endin
</CsInstruments>
<CsScore>
i 1 0 1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Prints:
kCycle = 1
gkArray[0] = 1
gkArray[1] = 2
gkArray[2] = 3
gkArray[3] = 4
gkArray[4] = 5
kCycle = 2
gkArray[0] = 1
gkArray[1] = 4
gkArray[2] = 9
gkArray[3] = 16
gkArray[4] = 25
kCycle = 3
gkArray[0] = 1
gkArray[1] = 16
gkArray[2] = 81
gkArray[3] = 256
gkArray[4] = 625
Time Loops
Until now, we have just discussed loops which are executed "as fast as possible", either at i-time or at k-time. But, in an audio programming language, time loops are of particular interest and importance. A time loop means, repeating any action after a certain amount of time. This amount of time can be equal to or different to the previous time loop. The action can be, for instance: playing a tone, or triggering an instrument, or calculating a new value for the movement of an envelope.
In Csound, the usual way of performing time loops, is the timout facility. The use of timout is a bit intricate, so some examples are given, starting from very simple to more complex ones.
Another way of performing time loops is by using a measurement of time or k-cycles. This method is also discussed and similar examples to those used for the timout opcode are given so that both methods can be compared.
timout Basics
The timout opcode refers to the fact that in the traditional way of working with Csound, each "note" (an "i" score event) has its own time. This is the duration of the note, given in the score by the duration parameter, abbreviated as "p3". A timout statement says: "I am now jumping out of this p3 duration and establishing my own time." This time will be repeated as long as the duration of the note allows it.
Let's see an example. This is a sine tone with a moving frequency, starting at 400 Hz and ending at 600 Hz. The duration of this movement is 3 seconds for the first note, and 5 seconds for the second note:
EXAMPLE 03C14_Timout_pre.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
instr 1
kFreq expseg 400, p3, 600
aTone poscil .2, kFreq, giSine
outs aTone, aTone
endin
</CsInstruments>
<CsScore>
i 1 0 3
i 1 4 5
</CsScore>
</CsoundSynthesizer>
Now we perform a time loop with timout which is 1 second long. So, for the first note, it will be repeated three times, and five times for the second note:
EXAMPLE 03C15_Timout_basics.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
instr 1
loop:
timout 0, 1, play
reinit loop
play:
kFreq expseg 400, 1, 600
aTone poscil .2, kFreq, giSine
outs aTone, aTone
endin
</CsInstruments>
<CsScore>
i 1 0 3
i 1 4 5
</CsScore>
</CsoundSynthesizer>
This is the general syntax of timout:
first_label:
timout istart, idur, second_label
reinit first_label
second_label:
... <any action you want to have here>
The first_label is an arbitrary word (followed by a colon) to mark the beginning of the time loop section. The istart argument for timout tells Csound, when the second_label section is to be executed. Usually istart is zero, telling Csound: execute the second_label section immediately, without any delay. The idur argument for timout defines for how many seconds the second_label section is to be executed before the time loop begins again. Note that the reinit first_label is necessary to start the second loop after idur seconds with a resetting of all the values. (See the explanations about reinitialization in the chapter Initialization And Performance Pass section 03A.)
As usual when you work with the reinit opcode, you can use a rireturn statement to constrain the reinit-pass. In this way you can have both, the timeloop section and the non-timeloop section in the body of an instrument:
EXAMPLE 03C16_Timeloop_and_not.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
instr 1
loop:
timout 0, 1, play
reinit loop
play:
kFreq1 expseg 400, 1, 600
aTone1 oscil3 .2, kFreq1, giSine
rireturn ;end of the time loop
kFreq2 expseg 400, p3, 600
aTone2 poscil .2, kFreq2, giSine
outs aTone1+aTone2, aTone1+aTone2
endin
</CsInstruments>
<CsScore>
i 1 0 3
i 1 4 5
</CsScore>
</CsoundSynthesizer>
timout Applications
In a time loop, it is very important to change the duration of the loop. This can be done either by referring to the duration of this note (p3) ...
EXAMPLE 03C17_Timout_different_durations.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
instr 1
loop:
timout 0, p3/5, play
reinit loop
play:
kFreq expseg 400, p3/5, 600
aTone poscil .2, kFreq, giSine
outs aTone, aTone
endin
</CsInstruments>
<CsScore>
i 1 0 3
i 1 4 5
</CsScore>
</CsoundSynthesizer>
... or by calculating new values for the loop duration on each reinit pass, for instance by random values:
EXAMPLE 03C18_Timout_random_durations.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
instr 1
loop:
idur random .5, 3 ;new value between 0.5 and 3 seconds each time
timout 0, idur, play
reinit loop
play:
kFreq expseg 400, idur, 600
aTone poscil .2, kFreq, giSine
outs aTone, aTone
endin
</CsInstruments>
<CsScore>
i 1 0 20
</CsScore>
</CsoundSynthesizer>
The applications discussed so far have the disadvantage that all the signals inside the time loop must definitely be finished or interrupted, when the next loop begins. In this way it is not possible to have any overlapping of events. To achieve this, the time loop can be used to simply trigger an event. This can be done with event_i or scoreline_i. In the following example, the time loop in instrument 1 triggers a new instance of instrument 2 with a duration of 1 to 5 seconds, every 0.5 to 2 seconds. So in most cases, the previous instance of instrument 2 will still be playing when the new instance is triggered. Random calculations are executed in instrument 2 so that each note will have a different pitch,creating a glissando effect:
EXAMPLE 03C19_Timout_trigger_events.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
instr 1
loop:
idurloop random .5, 2 ;duration of each loop
timout 0, idurloop, play
reinit loop
play:
idurins random 1, 5 ;duration of the triggered instrument
event_i "i", 2, 0, idurins ;triggers instrument 2
endin
instr 2
ifreq1 random 600, 1000 ;starting frequency
idiff random 100, 300 ;difference to final frequency
ifreq2 = ifreq1 - idiff ;final frequency
kFreq expseg ifreq1, p3, ifreq2 ;glissando
iMaxdb random -12, 0 ;peak randomly between -12 and 0 dB
kAmp transeg ampdb(iMaxdb), p3, -10, 0 ;envelope
aTone poscil kAmp, kFreq, giSine
outs aTone, aTone
endin
</CsInstruments>
<CsScore>
i 1 0 30
</CsScore>
</CsoundSynthesizer>
The last application of a time loop with the timout opcode which is shown here, is a randomly moving envelope. If you want to create an envelope in Csound which moves between a lower and an upper limit, and has one new random value in a certain time span (for instance, once a second), the time loop with timout is one way to achieve it. A line movement must be performed in each time loop, from a given starting value to a new evaluated final value. Then, in the next loop, the previous final value must be set as the new starting value, and so on. Here is a possible solution:
EXAMPLE 03C20_Timout_random_envelope.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
seed 0
instr 1
iupper = 0; upper and ...
ilower = -24; ... lower limit in dB
ival1 random ilower, iupper; starting value
loop:
idurloop random .5, 2; duration of each loop
timout 0, idurloop, play
reinit loop
play:
ival2 random ilower, iupper; final value
kdb linseg ival1, idurloop, ival2
ival1 = ival2; let ival2 be ival1 for next loop
rireturn ;end reinit section
aTone poscil ampdb(kdb), 400, giSine
outs aTone, aTone
endin
</CsInstruments>
<CsScore>
i 1 0 30
</CsScore>
</CsoundSynthesizer>
Note that in this case the oscillator has been put after the time loop section (which is terminated by the rireturn statement. Otherwise the oscillator would start afresh with zero phase in each time loop, thus producing clicks.
Time Loops by using the metro Opcode
The metro opcode outputs a "1" at distinct times, otherwise it outputs a "0". The frequency of this "banging" (which is in some way similar to the metro objects in PD or Max) is given by the kfreq input argument. So the output of metro offers a simple and intuitive method for controlling time loops, if you use it to trigger a separate instrument which then carries out another job. Below is a simple example for calling a subinstrument twice per second:
EXAMPLE 03C21_Timeloop_metro.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1; triggering instrument
kTrig metro 2; outputs "1" twice a second
if kTrig == 1 then
event "i", 2, 0, 1
endif
endin
instr 2; triggered instrument
aSig oscils .2, 400, 0
aEnv transeg 1, p3, -10, 0
outs aSig*aEnv, aSig*aEnv
endin
</CsInstruments>
<CsScore>
i 1 0 10
</CsScore>
</CsoundSynthesizer>
The example which is given above (03C19_Timout_trigger_events.csd) as a flexible time loop by timout, can be done with the metro opcode in this way:
EXAMPLE 03C22_Metro_trigger_events.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
seed 0
instr 1
kfreq init 1; give a start value for the trigger frequency
kTrig metro kfreq
if kTrig == 1 then ;if trigger impulse:
kdur random 1, 5; random duration for instr 2
event "i", 2, 0, kdur; call instr 2
kfreq random .5, 2; set new value for trigger frequency
endif
endin
instr 2
ifreq1 random 600, 1000; starting frequency
idiff random 100, 300; difference to final frequency
ifreq2 = ifreq1 - idiff; final frequency
kFreq expseg ifreq1, p3, ifreq2; glissando
iMaxdb random -12, 0; peak randomly between -12 and 0 dB
kAmp transeg ampdb(iMaxdb), p3, -10, 0; envelope
aTone poscil kAmp, kFreq, giSine
outs aTone, aTone
endin
</CsInstruments>
<CsScore>
i 1 0 30
</CsScore>
</CsoundSynthesizer>
Note the differences in working with the metro opcode compared to the timout feature:
- As metro works at k-time, you must use the k-variants of event or scoreline to call the subinstrument. With timout you must use the i-variants of event or scoreline (event_i and scoreline_i), because it uses reinitialization for performing the time loops.
- You must select the one k-cycle where the metro opcode sends a "1". This is done with an if-statement. The rest of the instrument is not affected. If you use timout, you usually must seperate the reinitialized from the not reinitialized section by a rireturn statement.
Links
Steven Yi: Control Flow (Part I = Csound Journal Spring 2006, Part 2 = Csound Journal Summer 2006)
- Since the release of the new parser (Csound 5.14), you can also write without parentheses.^
- Instead of using "od" you can also use "enduntil" in the until loop.^
Csound: FUNCTIONTABLES
FUNCTION TABLES
Note: This chapter was written before arrays had been introduced into Csound. Now the usage of arrays is in some situations preferable to using function tables. Have a look in chapter 03E to see how you can use arrays.
A function table is essentially the same as what other audio programming languages might call a buffer, a table, a list or an array. It is a place where data can be stored in an ordered way. Each function table has a size: how much data (in Csound, just numbers) it can store. Each value in the table can be accessed by an index, counting from 0 to size-1. For instance, if you have a function table with a size of 10, and the numbers [1.1 2.2 3.3 5.5 8.8 13.13 21.21 34.34 55.55 89.89] in it, this is the relation of value and index:
| VALUE | 1.1 | 2.2 | 3.3 | 5.5 | 8.8 | 13.13 | 21.21 | 34.34 | 55.55 | 89.89 |
| INDEX | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
So, if you want to retrieve the value 13.13, you must point to the value stored under index 5.
The use of function tables is manifold. A function table can contain pitch values to which you may refer using the input of a MIDI keyboard. A function table can contain a model of a waveform which is read periodically by an oscillator. You can record live audio input in a function table, and then play it back. There are many more applications, all using the fast access (because function tables are stored in RAM) and flexible use of function tables.
How to Generate a Function Table
Each function table must be created before it can be used. Even if you want to write values later, you must first create an empty table, because you must initially reserve some space in memory for it.
Each creation of a function table in Csound is performed by one of the GEN Routines. Each GEN Routine generates a function table in a particular way: GEN01 transfers audio samples from a soundfile into a table, GEN02 stores values we define explicitly one by one, GEN10 calculates a waveform using user-defined weightings of harmonically related sinusoids, GEN20 generates window functions typically used for granular synthesis, and so on. There is a good overview in the Csound Manual of all existing GEN Routines. Here we will explain their general use and provide some simple examples using commonly used GEN routines.
GEN02 and General Parameters for GEN Routines
Let's start with our example described above and write the 10 numbers into a function table with 10 storage locations. For this task use of a GEN02 function table is required. A short description of GEN02 from the manual reads as follows:
f # time size 2 v1 v2 v3 ...
This is the traditional way of creating a function table by use of an "f statement" or an "f score event" (in a manner similar to the use of "i score events" to call instrument instances). The input parameters after the "f" are as follows:
- #: a number (as positive integer) for this function table;
- time: at what time, in relation to the passage of the score, the function table is created (usually 0: from the beginning);
- size: the size of the function table. A little care is required: in the early days of Csound only power-of-two sizes were possible for function tables (2, 4, 8, 16, ...); nowadays almost all GEN Routines accepts other sizes, but these non-power-of-two sizes must be declared as negative numbers!
- 2: the number of the GEN Routine which is used to generate the table, and here is another important point which must be borne in mind: by default, Csound normalizes the table values. This means that the maximum is scaled to +1 if positive, and to -1 if negative. All other values in the table are then scaled by the same factor that was required to scale the maximum to +1 or -1. To prevent Csound from normalizing, a negative number can be given as GEN number (in this example, the GEN routine number will be given as -2 instead of 2).
- v1 v2 v3 ...: the values which are written into the function table.
The example below demonstrates how the values [1.1 2.2 3.3 5.5 8.8 13.13 21.21 34.34 55.55 89.89] can be stored in a function table using an f-statement in the score. Two versions are created: an unnormalised version (table number 1) and an normalised version (table number 2). The difference in their contents will be demonstrated.
EXAMPLE 03D01_Table_norm_notNorm.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Joachim Heintz
instr 1 ;prints the values of table 1 or 2
prints "%nFunction Table %d:%n", p4
indx init 0
loop:
ival table indx, p4
prints "Index %d = %f%n", indx, ival
loop_lt indx, 1, 10, loop
endin
</CsInstruments>
<CsScore>
f 1 0 -10 -2 1.1 2.2 3.3 5.5 8.8 13.13 21.21 34.34 55.55 89.89; not normalized
f 2 0 -10 2 1.1 2.2 3.3 5.5 8.8 13.13 21.21 34.34 55.55 89.89; normalized
i 1 0 0 1; prints function table 1
i 1 0 0 2; prints function table 2
</CsScore>
</CsoundSynthesizer>
Instrument 1 simply reads and prints (to the terminal) the values of the table. Notice the difference in values read, whether the table is normalized (positive GEN number) or not normalized (negative GEN number).
Using the ftgen opcode is a more modern way of creating a function table, which is generally preferable to the old way of writing an f-statement in the score.1 The syntax is explained below:
giVar ftgen ifn, itime, isize, igen, iarg1 [, iarg2 [, ...]]
- giVar: a variable name. Each function is stored in an i-variable. Usually you want to have access to it from every instrument, so a gi-variable (global initialization variable) is given.
- ifn: a number for the function table. If you type in 0, you give Csound the job to choose a number, which is mostly preferable.
The other parameters (size, GEN number, individual arguments) are the same as in the f-statement in the score. As this GEN call is now a part of the orchestra, each argument is separated from the next by a comma (not by a space or tab like in the score).
So this is the same example as above, but now with the function tables being generated in the orchestra header:
EXAMPLE 03D02_Table_ftgen.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Joachim Heintz
giFt1 ftgen 1, 0, -10, -2, 1.1, 2.2, 3.3, 5.5, 8.8, 13.13, 21.21, 34.34, 55.55, 89.89
giFt2 ftgen 2, 0, -10, 2, 1.1, 2.2, 3.3, 5.5, 8.8, 13.13, 21.21, 34.34, 55.55, 89.89
instr 1; prints the values of table 1 or 2
prints "%nFunction Table %d:%n", p4
indx init 0
loop:
ival table indx, p4
prints "Index %d = %f%n", indx, ival
loop_lt indx, 1, 10, loop
endin
</CsInstruments>
<CsScore>
i 1 0 0 1; prints function table 1
i 1 0 0 2; prints function table 2
</CsScore>
</CsoundSynthesizer>
GEN01: Importing a Soundfile
GEN01 is used for importing soundfiles stored on disk into the computer's RAM, ready for for use by a number of Csound's opcodes in the orchestra. A typical ftgen statement for this import might be the following:
varname ifn itime isize igen Sfilnam iskip iformat ichn giFile ftgen 0, 0, 0, 1, "myfile.wav", 0, 0, 0
- varname, ifn, itime: These arguments have the same meaning as explained above in reference to GEN02. Note that on this occasion the function table number (ifn) has been defined using a zero. This means that Csound will automatically assign a unique function table number. This number will also be held by the variable giFile which we will normally use to reference the function table anyway so its actual value will not be important to us. If you are interested you can print the value of giFile (ifn) out. If no other tables are defined, it will be 101 and subsequent tables, also using automatically assigned table numbers, will follow accordingly: 102, 103 etc.
- isize: Usually you won't know the length of your soundfile in samples, and want to have a table length which includes exactly all the samples. This is done by setting isize=0. (Note that some opcodes may need a power-of-two table. In this case you can not use this option, but must calculate the next larger power-of-two value as size for the function table.)
- igen: As explained in the previous subchapter, this is always the place for indicating the number of the GEN Routine which must be used. As always, a positive number means normalizing, which is often convenient for audio samples.
- Sfilnam: The name of the soundfile in double quotes. Similar to other audio programming languages, Csound recognizes just the name if your .csd and the soundfile are in the same folder. Otherwise, give the full path. (You can also include the folder via the "SSDIR" variable, or add the folder via the "--env:NAME+=VALUE" option.)
- iskip: The time in seconds you want to skip at the beginning of the soundfile. 0 means reading from the beginning of the file.
- iformat: The format of the amplitude samples in the soundfile, e.g. 16 bit, 24 bit etc. Usually providing 0 here is sufficient, in which case Csound will read the sample format form the soundfile header.
- ichn: 1 = read the first channel of the soundfile into the table, 2 = read the second channel, etc. 0 means that all channels are read. Note that only certain opcodes are able to properly make use of multichannel audio stored in function tables.
The following example loads a short sample into RAM via a function table and then plays it. You can download the sample here (or replace it with one of your own). Copy the text below, save it to the same location as the "fox.wav" soundfile (or add the folder via the "--env:NAME+=VALUE" option),2 and it should work. Reading the function table here is done using the poscil3 opcode which can deal with non-power-of-two tables.
EXAMPLE 03D03_Sample_to_table.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSample ftgen 0, 0, 0, 1, "fox.wav", 0, 0, 1
instr 1
itablen = ftlen(giSample) ;length of the table
idur = itablen / sr ;duration
aSamp poscil3 .5, 1/idur, giSample
outs aSamp, aSamp
endin
</CsInstruments>
<CsScore>
i 1 0 2.757
</CsScore>
</CsoundSynthesizer>
GEN10: Creating a Waveform
The third example for generating a function table covers a classic case: building a function table which stores one cycle of a waveform. This waveform will then be read by an oscillator to produce a sound.
There are many GEN Routines which can be used to achieve this. The simplest one is GEN10. It produces a waveform by adding sine waves which have the "harmonic" frequency relationship 1 : 2 : 3 : 4 ... After the usual arguments for function table number, start, size and gen routine number, which are the first four arguments in ftgen for all GEN Routines, with GEN10 you must specify the relative strengths of the harmonics. So, if you just provide one argument, you will end up with a sine wave (1st harmonic). The next argument is the strength of the 2nd harmonic, then the 3rd, and so on. In this way, you can build approximations of the standard harmonic waveforms by the addition of sinusoids. This is done in the next example by instruments 1-5. Instrument 6 uses the sine wavetable twice: for generating both the sound and the envelope.
EXAMPLE 03D04_Standard_waveforms_with_GEN10.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
giSaw ftgen 0, 0, 2^10, 10, 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9
giSquare ftgen 0, 0, 2^10, 10, 1, 0, 1/3, 0, 1/5, 0, 1/7, 0, 1/9
giTri ftgen 0, 0, 2^10, 10, 1, 0, -1/9, 0, 1/25, 0, -1/49, 0, 1/81
giImp ftgen 0, 0, 2^10, 10, 1, 1, 1, 1, 1, 1, 1, 1, 1
instr 1 ;plays the sine wavetable
aSine poscil .2, 400, giSine
aEnv linen aSine, .01, p3, .05
outs aEnv, aEnv
endin
instr 2 ;plays the saw wavetable
aSaw poscil .2, 400, giSaw
aEnv linen aSaw, .01, p3, .05
outs aEnv, aEnv
endin
instr 3 ;plays the square wavetable
aSqu poscil .2, 400, giSquare
aEnv linen aSqu, .01, p3, .05
outs aEnv, aEnv
endin
instr 4 ;plays the triangular wavetable
aTri poscil .2, 400, giTri
aEnv linen aTri, .01, p3, .05
outs aEnv, aEnv
endin
instr 5 ;plays the impulse wavetable
aImp poscil .2, 400, giImp
aEnv linen aImp, .01, p3, .05
outs aEnv, aEnv
endin
instr 6 ;plays a sine and uses the first half of its shape as envelope
aEnv poscil .2, 1/6, giSine
aSine poscil aEnv, 400, giSine
outs aSine, aSine
endin
</CsInstruments>
<CsScore>
i 1 0 3
i 2 4 3
i 3 8 3
i 4 12 3
i 5 16 3
i 6 20 3
</CsScore>
</CsoundSynthesizer>
How to Write Values to a Function Table
As we have seen, GEN Routines generate function tables, and by doing this, they write values into them according to various methods, but in certain cases you might first want to create an empty table, and then write the values into it later or you might want to alter the default values held in a function table. The following section demonstrates how to do this.
To be precise, it is not actually correct to talk about an "empty table". If Csound creates an "empty" table, in fact it writes zeros to the indices which are not specified. Perhaps the easiest method of creating an "empty" table for 100 values is shown below:
giEmpty ftgen 0, 0, -100, 2, 0
The simplest to use opcode that writes values to existing function tables during a note's performance is tablew and its i-time equivalent is tableiw. Note that you may have problems with some features if your table is not a power-of-two size. In this case, you can also use tabw / tabw_i, but they don't have the offset- and the wraparound-feature. As usual, you must differentiate if your signal (variable) is i-rate, k-rate or a-rate. The usage is simple and differs just in the class of values you want to write to the table (i-, k- or a-variables):
tableiw isig, indx, ifn [, ixmode] [, ixoff] [, iwgmode]
tablew ksig, kndx, ifn [, ixmode] [, ixoff] [, iwgmode]
tablew asig, andx, ifn [, ixmode] [, ixoff] [, iwgmode]
- isig, ksig, asig is the value (variable) you want to write into a specified location of the table;
- indx, kndx, andx is the location (index) where you will write the value;
- ifn is the function table you want to write to;
- ixmode gives the choice to write by raw indices (counting from 0 to size-1), or by a normalized writing mode in which the start and end of each table are always referred as 0 and 1 (not depending on the length of the table). The default is ixmode=0 which means the raw index mode. A value not equal to zero for ixmode changes to the normalized index mode.
- ixoff (default=0) gives an index offset. So, if indx=0 and ixoff=5, you will write at index 5.
- iwgmode tells what you want to do if your index is larger than the size of the table. If iwgmode=0 (default), any index larger than possible is written at the last possible index. If iwgmode=1, the indices are wrapped around. For instance, if your table size is 8, and your index is 10, in the wraparound mode the value will be written at index 2.
Here are some examples for i-, k- and a-rate values.
i-Rate Example
The following example calculates the first 12 values of a Fibonacci series and writes them to a table. An empty table has first been created in the header (filled with zeros), then instrument 1 calculates the values in an i-time loop and writes them to the table using tableiw. Instrument 2 simply prints all the values in a list to the terminal.
EXAMPLE 03D05_Write_Fibo_to_table.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Joachim Heintz
giFt ftgen 0, 0, -12, -2, 0
instr 1; calculates first 12 fibonacci values and writes them to giFt
istart = 1
inext = 2
indx = 0
loop:
tableiw istart, indx, giFt ;writes istart to table
istartold = istart ;keep previous value of istart
istart = inext ;reset istart for next loop
inext = istartold + inext ;reset inext for next loop
loop_lt indx, 1, 12, loop
endin
instr 2; prints the values of the table
prints "%nContent of Function Table:%n"
indx init 0
loop:
ival table indx, giFt
prints "Index %d = %f%n", indx, ival
loop_lt indx, 1, ftlen(giFt), loop
endin
</CsInstruments>
<CsScore>
i 1 0 0
i 2 0 0
</CsScore>
</CsoundSynthesizer>
k-Rate Example
The next example writes a k-signal continuously into a table. This can be used to record any kind of user input, for instance by MIDI or widgets. It can also be used to record random movements of k-signals, like here:
EXAMPLE 03D06_Record_ksig_to_table.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giFt ftgen 0, 0, -5*kr, 2, 0; size for 5 seconds of recording
giWave ftgen 0, 0, 2^10, 10, 1, .5, .3, .1; waveform for oscillator
seed 0
; - recording of a random frequency movement for 5 seconds, and playing it
instr 1
kFreq randomi 400, 1000, 1 ;random frequency
aSnd poscil .2, kFreq, giWave ;play it
outs aSnd, aSnd
;;record the k-signal
prints "RECORDING!%n"
;create a writing pointer in the table,
;moving in 5 seconds from index 0 to the end
kindx linseg 0, 5, ftlen(giFt)
;write the k-signal
tablew kFreq, kindx, giFt
endin
instr 2; read the values of the table and play it again
;;read the k-signal
prints "PLAYING!%n"
;create a reading pointer in the table,
;moving in 5 seconds from index 0 to the end
kindx linseg 0, 5, ftlen(giFt)
;read the k-signal
kFreq table kindx, giFt
aSnd oscil3 .2, kFreq, giWave; play it
outs aSnd, aSnd
endin
</CsInstruments>
<CsScore>
i 1 0 5
i 2 6 5
</CsScore>
</CsoundSynthesizer>
As you see, this typical case of writing k-values to a table requires a changing value for the index, otherwise tablew will continually overwrite at the same table location. This changing value can be created using the line or linseg opcodes - as was done here - or by using a phasor. A phasor moves continuously from 0 to 1 at a user-defined frequency. For example, if you want a phasor to move from 0 to 1 in 5 seconds, you must set the frequency to 1/5. Upon reaching 1, the phasor will wrap-around to zero and begin again. Note that phasor can also be given a negative frequency in which case it moves in reverse from 1 to zero then wrapping around to 1. By setting the ixmode argument of tablew to 1, you can use the phasor output directly as writing pointer. Below is an alternative version of instrument 1 from the previous example, this time using phasor to generate the index values:
instr 1; recording of a random frequency movement for 5 seconds, and playing it
kFreq randomi 400, 1000, 1; random frequency
aSnd oscil3 .2, kFreq, giWave; play it
outs aSnd, aSnd
;;record the k-signal with a phasor as index
prints "RECORDING!%n"
;create a writing pointer in the table,
;moving in 5 seconds from index 0 to the end
kindx phasor 1/5
;write the k-signal
tablew kFreq, kindx, giFt, 1
endin
a-Rate Example
Recording an audio signal is quite similar to recording a control signal. You just need an a-signal to provide input values and also an index that changes at a-rate. The next example first records a randomly generated audio signal and then plays it back. It then records the live audio input for 5 seconds and subsequently plays it back.
EXAMPLE 03D07_Record_audio_to_table.csd
<CsoundSynthesizer>
<CsOptions>
-iadc -odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giFt ftgen 0, 0, -5*sr, 2, 0; size for 5 seconds of recording audio
seed 0
instr 1 ;generating a band filtered noise for 5 seconds, and recording it
aNois rand .2
kCfreq randomi 200, 2000, 3; random center frequency
aFilt butbp aNois, kCfreq, kCfreq/10; filtered noise
aBal balance aFilt, aNois, 1; balance amplitude
outs aBal, aBal
;;record the audiosignal with a phasor as index
prints "RECORDING FILTERED NOISE!%n"
;create a writing pointer in the table,
;moving in 5 seconds from index 0 to the end
aindx phasor 1/5
;write the k-signal
tablew aBal, aindx, giFt, 1
endin
instr 2 ;read the values of the table and play it
prints "PLAYING FILTERED NOISE!%n"
aindx phasor 1/5
aSnd table3 aindx, giFt, 1
outs aSnd, aSnd
endin
instr 3 ;record live input
ktim timeinsts ; playing time of the instrument in seconds
prints "PLEASE GIVE YOUR LIVE INPUT AFTER THE BEEP!%n"
kBeepEnv linseg 0, 1, 0, .01, 1, .5, 1, .01, 0
aBeep oscils .2, 600, 0
outs aBeep*kBeepEnv, aBeep*kBeepEnv
;;record the audiosignal after 2 seconds
if ktim > 2 then
ain inch 1
printks "RECORDING LIVE INPUT!%n", 10
;create a writing pointer in the table,
;moving in 5 seconds from index 0 to the end
aindx phasor 1/5
;write the k-signal
tablew ain, aindx, giFt, 1
endif
endin
instr 4 ;read the values from the table and play it
prints "PLAYING LIVE INPUT!%n"
aindx phasor 1/5
aSnd table3 aindx, giFt, 1
outs aSnd, aSnd
endin
</CsInstruments>
<CsScore>
i 1 0 5 ; record 5 seconds of generated audio to a table
i 2 6 5 ; play back the recording of generated audio
i 3 12 7 ; record 5 seconds of live audio to a table
i 4 20 5 ; play back the recording of live audio
</CsScore>
</CsoundSynthesizer>
How to Retrieve Values from a Function Table
There are two methods of reading table values. You can either use the table / tab opcodes, which are universally usable, but need an index; or you can use an oscillator for reading a table at k-rate or a-rate.
The table Opcode
The table opcode is quite similar in syntax to the tableiw/tablew opcodes (which are explained above). It is simply its counterpart for reading values from a function table instead of writing them. Its output can be either an i-, k- or a-rate signal and the value type of the output automatically selects either the a- k- or a-rate version of the opcode. The first input is an index at the appropriate rate (i-index for i-output, k-index for k-output, a-index for a-output). The other arguments are as explained above for tableiw/tablew:
ires table indx, ifn [, ixmode] [, ixoff] [, iwrap] kres table kndx, ifn [, ixmode] [, ixoff] [, iwrap] ares table andx, ifn [, ixmode] [, ixoff] [, iwrap]
As table reading often requires interpolation between the table values - for instance if you read k- or a-values faster or slower than they have been written in the table - Csound offers two descendants of table for interpolation: tablei interpolates linearly, whilst table3 performs cubic interpolation (which is generally preferable but is computationally slightly more expensive) and when CPU cycles are no object, tablexkt can be used for ultimate interpolating quality.3
Another variant is the tab_i / tab opcode which misses some features but may be preferable in some situations. If you have any problems in reading non-power-of-two tables, give them a try. They should also be faster than the table (and variants thereof) opcode, but you must take care: they include fewer built-in protection measures than table, tablei and table3 and if they are given index values that exceed the table size Csound will stop and report a performance error.
Examples of the use of the table opcodes can be found in the earlier examples in the How-To-Write-Values... section.
Oscillators
It is normal to read tables that contain a single cycle of an audio waveform using an oscillator but you can actually read any table using an oscillator, either at a- or at k-rate. The advantage is that you needn't create an index signal. You can simply specify the frequency of the oscillator (the opcode creates the required index internally based on the asked for frequency).
You should bear in mind that many of the oscillators in Csound will work only with power-of-two table sizes. The poscil/poscil3 opcodes do not have this restriction and offer a high precision, because they work with floating point indices, so in general it is recommended to use them. Below is an example that demonstrates both reading a k-rate and an a-rate signal from a buffer with poscil3 (an oscillator with a cubic interpolation):
EXAMPLE 03D08_RecPlay_ak_signals.csd
<CsoundSynthesizer>
<CsOptions>
-iadc -odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
; -- size for 5 seconds of recording control data
giControl ftgen 0, 0, -5*kr, 2, 0
; -- size for 5 seconds of recording audio data
giAudio ftgen 0, 0, -5*sr, 2, 0
giWave ftgen 0, 0, 2^10, 10, 1, .5, .3, .1; waveform for oscillator
seed 0
; -- ;recording of a random frequency movement for 5 seconds, and playing it
instr 1
kFreq randomi 400, 1000, 1; random frequency
aSnd poscil .2, kFreq, giWave; play it
outs aSnd, aSnd
;;record the k-signal with a phasor as index
prints "RECORDING RANDOM CONTROL SIGNAL!%n"
;create a writing pointer in the table,
;moving in 5 seconds from index 0 to the end
kindx phasor 1/5
;write the k-signal
tablew kFreq, kindx, giControl, 1
endin
instr 2; read the values of the table and play it with poscil
prints "PLAYING CONTROL SIGNAL!%n"
kFreq poscil 1, 1/5, giControl
aSnd poscil .2, kFreq, giWave; play it
outs aSnd, aSnd
endin
instr 3; record live input
ktim timeinsts ; playing time of the instrument in seconds
prints "PLEASE GIVE YOUR LIVE INPUT AFTER THE BEEP!%n"
kBeepEnv linseg 0, 1, 0, .01, 1, .5, 1, .01, 0
aBeep oscils .2, 600, 0
outs aBeep*kBeepEnv, aBeep*kBeepEnv
;;record the audiosignal after 2 seconds
if ktim > 2 then
ain inch 1
printks "RECORDING LIVE INPUT!%n", 10
;create a writing pointer in the table,
;moving in 5 seconds from index 0 to the end
aindx phasor 1/5
;write the k-signal
tablew ain, aindx, giAudio, 1
endif
endin
instr 4; read the values from the table and play it with poscil
prints "PLAYING LIVE INPUT!%n"
aSnd poscil .5, 1/5, giAudio
outs aSnd, aSnd
endin
</CsInstruments>
<CsScore>
i 1 0 5
i 2 6 5
i 3 12 7
i 4 20 5
</CsScore>
</CsoundSynthesizer>
Saving the Contents of a Function Table to a File
A function table exists only as long as you run the Csound instance which has created it. If Csound terminates, all the data is lost. If you want to save the data for later use, you must write them to a file. There are several cases, depending firstly on whether you write at i-time or at k-time and secondly on what kind of file you want to write to.
Writing a File in Csound's ftsave Format at i-Time or k-Time
Any function table in Csound can be easily written to a file using the ftsave (i-time) or ftsavek (k-time) opcode. Their use is very simple. The first argument specifies the filename (in double quotes), the second argument selects between a text format (non zero) or a binary format (zero) output. Finally you just provide the number of the function table(s) to save.
With the following example, you should end up with two textfiles in the same folder as your .csd: "i-time_save.txt" saves function table 1 (a sine wave) at i-time; "k-time_save.txt" saves function table 2 (a linear increment produced during the performance) at k-time.
EXAMPLE 03D09_ftsave.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giWave ftgen 1, 0, 2^7, 10, 1; sine with 128 points
giControl ftgen 2, 0, -kr, 2, 0; size for 1 second of recording control data
seed 0
instr 1; saving giWave at i-time
ftsave "i-time_save.txt", 1, 1
endin
instr 2; recording of a line transition between 0 and 1 for one second
kline linseg 0, 1, 1
tabw kline, kline, giControl, 1
endin
instr 3; saving giWave at k-time
ftsave "k-time_save.txt", 1, 2
endin
</CsInstruments>
<CsScore>
i 1 0 0
i 2 0 1
i 3 1 .1
</CsScore>
</CsoundSynthesizer>
The counterpart to ftsave/ftsavek are the ftload/ftloadk opcodes. You can use them to load the saved files into function tables.
Writing a Soundfile from a Recorded Function Table
If you have recorded your live-input to a buffer, you may want to save your buffer as a soundfile. There is no opcode in Csound which does that, but it can be done by using a k-rate loop and the fout opcode. This is shown in the next example in instrument 2. First instrument 1 records your live input. Then instrument 2 creates a soundfile "testwrite.wav" containing this audio in the same folder as your .csd. This is done at the first k-cycle of instrument 2, by repeatedly reading the table values and writing them as an audio signal to disk. After this is done, the instrument is turned off by executing the turnoff statement.
EXAMPLE 03D10_Table_to_soundfile.csd
<CsoundSynthesizer>
<CsOptions>
-i adc
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
; -- size for 5 seconds of recording audio data
giAudio ftgen 0, 0, -5*sr, 2, 0
instr 1 ;record live input
ktim timeinsts ; playing time of the instrument in seconds
prints "PLEASE GIVE YOUR LIVE INPUT AFTER THE BEEP!%n"
kBeepEnv linseg 0, 1, 0, .01, 1, .5, 1, .01, 0
aBeep oscils .2, 600, 0
outs aBeep*kBeepEnv, aBeep*kBeepEnv
;;record the audiosignal after 2 seconds
if ktim > 2 then
ain inch 1
printks "RECORDING LIVE INPUT!%n", 10
;create a writing pointer in the table,
;moving in 5 seconds from index 0 to the end
aindx phasor 1/5
;write the k-signal
tablew ain, aindx, giAudio, 1
endif
endin
instr 2; write the giAudio table to a soundfile
Soutname = "testwrite.wav"; name of the output file
iformat = 14; write as 16 bit wav file
itablen = ftlen(giAudio); length of the table in samples
kcnt init 0; set the counter to 0 at start
loop:
kcnt = kcnt+ksmps; next value (e.g. 10 if ksmps=10)
andx interp kcnt-1; calculate audio index (e.g. from 0 to 9)
asig tab andx, giAudio; read the table values as audio signal
fout Soutname, iformat, asig; write asig to a file
if kcnt <= itablen-ksmps kgoto loop; go back as long there is something to do
turnoff ; terminate the instrument
endin
</CsInstruments>
<CsScore>
i 1 0 7
i 2 7 .1
</CsScore>
</CsoundSynthesizer>
This code can also be used in the form of a User Defined Opcode. It can be found here.
Other GEN Routine Highlights
GEN05, GEN07, GEN25, GEN27 and GEN16 are useful for creating envelopes. GEN07 and GEN27 create functions table in the manner of the linseg opcode - with GEN07 the user defines segment duration whereas in GEN27 the user defines the absolute time for each breakpoint from the beginning of the envelope. GEN05 and GEN25 operate similarly to GEN07 and GEN27 except that envelope segments are exponential in shape. GEN16 also create an envelope in breakpoint fashion but it allows the user to specify the curvature of each segment individually (concave - straight - convex).
GEN17, GEN41 and GEN42 are used the generate histogram-type functions which may prove useful in algorithmic composition and work with probabilities.
GEN09 and GEN19 are developments of GEN10 and are useful in additive synthesis.
GEN11 is a GEN routine version of the gbuzz opcode and as it is a fixed waveform (unlike gbuzz) it can be a useful and efficient sound source in subtractive synthesis.
GEN08
f # time size 8 a n1 b n2 c n3 d ...
GEN08 creates a curved function that forms the smoothest possible line between a sequence of user defined break-points. This GEN routine can be useful for the creation of window functions for use as envelope shapes or in granular synthesis. In forming a smooth curve, GEN08 may create apexes that extend well above or below any of the defined values. For this reason GEN08 is mostly used with post-normalisation turned on, i.e. a minus sign is not added to the GEN number when the function table is defined. Here are some examples of GEN08 tables:
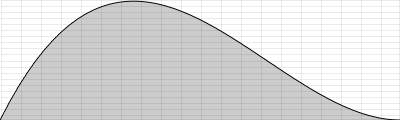
f 1 0 1024 8 0 1 1 1023 0
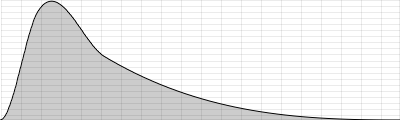
f 2 0 1024 8 0 97 1 170 0.583 757 0

f 3 0 1024 8 0 1 0.145 166 0.724 857 0
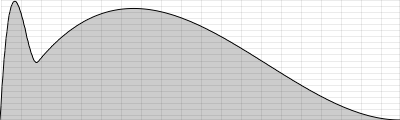
f 4 0 1024 8 0 1 0.079 96 0.645 927 0
GEN16
f # time size 16 val1 dur1 type1 val2 [dur2 type2 val3 ... typeX valN]
GEN16 allows the creation of envelope functions using a sequence of user defined breakpoints. Additionally for each segment of the envelope we can define a curvature. The nature of the curvature – concave or convex – will also depend upon the direction of the segment: rising or falling. For example, positive curvature values will result in concave curves in rising segments and convex curves in falling segments. The opposite applies if the curvature value is negative. Below are some examples of GEN16 function tables:
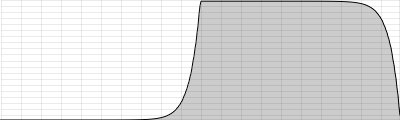
f 1 0 1024 16 0 512 20 1 512 20 0

f 2 0 1024 16 0 512 4 1 512 4 0

f 3 0 1024 16 0 512 0 1 512 0 0
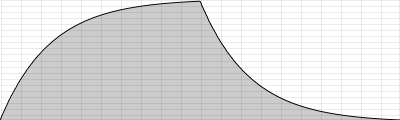
f 4 0 1024 16 0 512 -4 1 512 -4 0
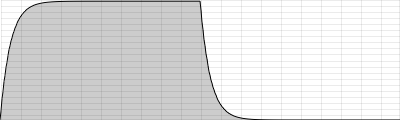
f 5 0 1024 16 0 512 -20 1 512 -20 0
GEN19
f # time size 19 pna stra phsa dcoa pnb strb phsb dcob ...
GEN19 follows on from GEN10 and GEN09 in terms of complexity and control options. It shares the basic concept of generating a harmonic waveform from stacked sinusoids but in addition to control over the strength of each partial (GEN10) and the partial number and phase (GEN09) it offers control over the DC offset of each partial. In addition to the creation of waveforms for use by audio oscillators other applications might be the creation of functions for LFOs and window functions for envelopes in granular synthesis. Below are some examples of GEN19:
f 1 0 1024 19 1 1 0 0 20 0.1 0 0
f 2 0 1024 -19 0.5 1 180 1
GEN30
f # time size 30 src minh maxh [ref_sr] [interp]
GEN30 uses FFT to create a band-limited version of a source waveform without band-limiting. We can create a sawtooth waveform by drawing one explicitly using GEN07 by used as an audio waveform this will create problems as it contains frequencies beyond the Nyquist frequency therefore will cause aliasing, particularly when higher notes are played. GEN30 can analyse this waveform and create a new one with a user defined lowest and highest partial. If we know what note we are going to play we can predict what the highest partial below the Nyquist frequency will be. For a given frequency, freq, the maximum number of harmonics that can be represented without aliasing can be derived using sr / (2 * freq).
Here are some examples of GEN30 function tables (the first table is actually a GEN07 generated sawtooth, the second two are GEN30 band-limited versions of the first):
f 1 0 1024 7 1 1024 -1
f 2 0 1024 30 1 1 20
f 3 0 1024 30 1 2 20
Related Opcodes
ftgen: Creates a function table in the orchestra using any GEN Routine.
table / tablei / table3: Read values from a function table at any rate, either by direct indexing (table), or by linear (tablei) or cubic (table3) interpolation. These opcodes provide many options and are safe because of boundary check, but you may have problems with non-power-of-two tables.
tab_i / tab: Read values from a function table at i-rate (tab_i), k-rate or a-rate (tab). Offer no interpolation and less options than the table opcodes, but they work also for non-power-of-two tables. They do not provide a boundary check, which makes them fast but also give the user the resposability not reading any value off the table boundaries.
tableiw / tablew: Write values to a function table at i-rate (tableiw), k-rate and a-rate (tablew). These opcodes provide many options and are safe because of boundary check, but you may have problems with non-power-of-two tables.
tabw_i / tabw: Write values to a function table at i-rate (tabw_i), k-rate or a-rate (tabw). Offer less options than the tableiw/tablew opcodes, but work also for non-power-of-two tables. They do not provide a boundary check, which makes them fast but also give the user the resposability not writing any value off the table boundaries.
poscil / poscil3: Precise oscillators for reading function tables at k- or a-rate, with linear (poscil) or cubic (poscil3) interpolation. They support also non-power-of-two tables, so it's usually recommended to use them instead of the older oscili/oscil3 opcodes. Poscil has also a-rate input for amplitude and frequency, while poscil3 has just k-rate input.
oscili / oscil3: The standard oscillators in Csound for reading function tables at k- or a-rate, with linear (oscili) or cubic (oscil3) interpolation. They support all rates for the amplitude and frequency input, but are restricted to power-of-two tables. Particularily for long tables and low frequencies they are not as precise as the poscil/poscil3 oscillators.
ftsave / ftsavek: Save a function table as a file, at i-time (ftsave) or k-time (ftsavek). This can be a text file or a binary file, but not a soundfile. If you want to save a soundfile, use the User Defined Opcode TableToSF.
ftload / ftloadk: Load a function table which has been written by ftsave/ftsavek.
line / linseg / phasor: Can be used to create index values which are needed to read/write k- or a-signals with the table/tablew or tab/tabw opcodes.
- ftgen is preferred mainly because you can refer to the function table by a variable name and must not deal with constant tables numbers. This will enhance the portability of orchestras and better facilitate the combining of multiple orchestras. It can also enhance the readability of an orchestra if a function table is located in the code nearer the instrument that uses it.^
- If your .csd file is, for instance, in the directory /home/jh/csound, and your sound file in the directory /home/jh/samples, you should add this inside the <CsOptions> tag:
--env:SSDIR+=/home/jh/samples. This means: 'Look also in /home/jh/sample as Sound Sample Directory (SSDIR)'
^ - For a general introduction about interpolation, see for instance http://en.wikipedia.org/wiki/Interpolation^
ARRAYS
One of the principal new features of Csound 6 is the support of arrays. This chapter aims to demonstrate how to use arrays using the methods currently implemented.
The outline of this chapter is as follows:
- Types of Arrays
- Dimensions
- i- or k-rate
- Local or Global
- Arrays of Strings
- Arrays of Audio Signals
- More on Array Rates
- Naming Conventions
- Creating an Array
- init
- array / fillarray
- genarray
- Basic Operations: len / slice
- Copy Arrays from/to Tables
- Copy Arrays from/to FFT Data
- Math Operations
- +, -, *, / on a Number
- +, -, *, / on a Second Array
- min / max / sum / scale
- Function Mapping on an Array: maparray
- Arrays in UDOs
Types of Arrays
Dimensions
One-dimensional arrays - also called vectors - are the most commonly used type of array, but in Csound6 you can also use arrays with two or more dimensions. The way in which the number of dimensions is designated is very similar to how it is done in other programming languages.
The code below denotes the second element of a one-dimensional array (as usual, indexing an element starts at zero, so kArr[0] would be the first element):
kArr[1]
The following denotes the second column in the third row of a two-dimensional array:
kArr[2][1]
Note that the square brackets are not used everywhere. This is explained in more detail below under 'Naming Conventions'.
i- or k-Rate
Like most other variables in Csound, arrays can be either i-rate or k-rate. An i-array can only be modified at init-time, and any operation on it is only performed once, at init-time. A k-array can be modified during the performance, and any (k-) operation on it will be performed in every k-cycle (!). Here is a very simple example:
EXAMPLE 03E01_i_k_arrays.csd
<CsoundSynthesizer> <CsOptions> -nm128 ;no sound and reduced messages </CsOptions> <CsInstruments> sr = 44100 ksmps = 4410 ;10 k-cycles per second instr 1 iArr[] fillarray 1, 2, 3 iArr[0] = iArr[0] + 10 prints " iArr[0] = %d\n\n", iArr[0] endin instr 2 kArr[] fillarray 1, 2, 3 kArr[0] = kArr[0] + 10 printks " kArr[0] = %d\n", 0, kArr[0] endin </CsInstruments> <CsScore> i 1 0 1 i 2 1 1 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
The output shows this:
iArr[0] = 11
kArr[0] = 11
kArr[0] = 21
kArr[0] = 31
kArr[0] = 41
kArr[0] = 51
kArr[0] = 61
kArr[0] = 71
kArr[0] = 81
kArr[0] = 91
kArr[0] = 101
Although both instruments run for one second, the operation to increment the first array value by ten is executed only once in the i-rate version of the array. But in the k-rate version, the incrementation is repeated in each k-cycle - in this case every 1/10 second, but usually something around every 1/1000 second. A good opportunity to throw off rendering power for useless repetitions, or to produce errors if you intentionally wanted to operate something only once ...
Local or Global
Like any other variable in Csound, an array usually has a local scope - this means that it is only recognized within the scope of the instrument in which it has been defined. If you want to use arrays in a globally (across instruments), then you have to prefix the variable name with the character g, (as is done with other types of global variable in Csound). The next example demonstrates local and global arrays at both i- and k-rate.
EXAMPLE 03E02_Local_vs_global_arrays.csd
<CsoundSynthesizer>
<CsOptions>
-nm128 ;no sound and reduced messages
</CsOptions>
<CsInstruments>
ksmps = 32
instr i_local
iArr[] fillarray 1, 2, 3
prints " iArr[0] = %d iArr[1] = %d iArr[2] = %d\n",
iArr[0], iArr[1], iArr[2]
endin
instr i_local_diff ;same name, different content
iArr[] fillarray 4, 5, 6
prints " iArr[0] = %d iArr[1] = %d iArr[2] = %d\n",
iArr[0], iArr[1], iArr[2]
endin
instr i_global
giArr[] fillarray 11, 12, 13
endin
instr i_global_read ;understands giArr though not defined here
prints " giArr[0] = %d giArr[1] = %d giArr[2] = %d\n",
giArr[0], giArr[1], giArr[2]
endin
instr k_local
kArr[] fillarray -1, -2, -3
printks " kArr[0] = %d kArr[1] = %d kArr[2] = %d\n",
0, kArr[0], kArr[1], kArr[2]
turnoff
endin
instr k_local_diff
kArr[] fillarray -4, -5, -6
printks " kArr[0] = %d kArr[1] = %d kArr[2] = %d\n",
0, kArr[0], kArr[1], kArr[2]
turnoff
endin
instr k_global
gkArr[] fillarray -11, -12, -13
turnoff
endin
instr k_global_read
printks " gkArr[0] = %d gkArr[1] = %d gkArr[2] = %d\n",
0, gkArr[0], gkArr[1], gkArr[2]
turnoff
endin
</CsInstruments>
<CsScore>
i "i_local" 0 0
i "i_local_diff" 0 0
i "i_global" 0 0
i "i_global_read" 0 0
i "k_local" 0 1
i "k_local_diff" 0 1
i "k_global" 0 1
i "k_global_read" 0 1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Arrays of Strings
So far we have discussed only arrays of numbers. It is also possible to have arrays of strings, which can be very useful in many situations, for instance while working with file paths.1 Here is a very simple example first, followed by a more extended one.
EXAMPLE 03E03_String_arrays.csd
<CsoundSynthesizer>
<CsOptions>
-nm128 ;no sound and reduced messages
</CsOptions>
<CsInstruments>
ksmps = 32
instr 1
String = "onetwothree"
S_Arr[] init 3
S_Arr[0] strsub String, 0, 3
S_Arr[1] strsub String, 3, 6
S_Arr[2] strsub String, 6
printf_i "S_Arr[0] = '%s'\nS_Arr[1] = '%s'\nS_Arr[2] = '%s'\n", 1,
S_Arr[0], S_Arr[1], S_Arr[2]
endin
</CsInstruments>
<CsScore>
i 1 0 1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
EXAMPLE 03E04_Anagram.csd
<CsoundSynthesizer>
<CsOptions>
-dnm0
</CsOptions>
<CsInstruments>
ksmps = 32
giArrLen = 5
gSArr[] init giArrLen
opcode StrAgrm, S, Sj
;changes the elements in Sin randomly, like in an anagram
Sin, iLen xin
if iLen == -1 then
iLen strlen Sin
endif
Sout = ""
;for all elements in Sin
iCnt = 0
iRange = iLen
loop:
;get one randomly
iRnd rnd31 iRange-.0001, 0
iRnd = int(abs(iRnd))
Sel strsub Sin, iRnd, iRnd+1
Sout strcat Sout, Sel
;take it out from Sin
Ssub1 strsub Sin, 0, iRnd
Ssub2 strsub Sin, iRnd+1
Sin strcat Ssub1, Ssub2
;adapt range (new length)
iRange = iRange-1
loop_lt iCnt, 1, iLen, loop
xout Sout
endop
instr 1
prints "Filling gSArr[] in instr %d at init-time!\n", p1
iCounter = 0
until (iCounter == giArrLen) do
S_new StrAgrm "csound"
gSArr[iCounter] = S_new
iCounter += 1
od
endin
instr 2
prints "Printing gSArr[] in instr %d at init-time:\n [", p1
iCounter = 0
until (iCounter == giArrLen) do
printf_i "%s ", iCounter+1, gSArr[iCounter]
iCounter += 1
od
prints "]\n"
endin
instr 3
printks "Printing gSArr[] in instr %d at perf-time:\n [", 0, p1
kcounter = 0
until (kcounter == giArrLen) do
printf "%s ", kcounter+1, gSArr[kcounter]
kcounter += 1
od
printks "]\n", 0
turnoff
endin
instr 4
prints "Modifying gSArr[] in instr %d at init-time!\n", p1
iCounter = 0
until (iCounter == giArrLen) do
S_new StrAgrm "csound"
gSArr[iCounter] = S_new
iCounter += 1
od
endin
instr 5
prints "Printing gSArr[] in instr %d at init-time:\n [", p1
iCounter = 0
until (iCounter == giArrLen) do
printf_i "%s ", iCounter+1, gSArr[iCounter]
iCounter += 1
od
prints "]\n"
endin
instr 6
kCycle timeinstk
printks "Modifying gSArr[] in instr %d at k-cycle %d!\n", 0,
p1, kCycle
kCounter = 0
until (kCounter == giArrLen) do
kChar random 33, 127
S_new sprintfk "%c ", int(kChar)
gSArr[kCounter] strcpyk S_new ;'=' should work but does not
kCounter += 1
od
if kCycle == 3 then
turnoff
endif
endin
instr 7
kCycle timeinstk
printks "Printing gSArr[] in instr %d at k-cycle %d:\n [",
0, p1, kCycle
kCounter = 0
until (kCounter == giArrLen) do
printf "%s ", kCounter+1, gSArr[kCounter]
kCounter += 1
od
printks "]\n", 0
if kCycle == 3 then
turnoff
endif
endin
</CsInstruments>
<CsScore>
i 1 0 1
i 2 0 1
i 3 0 1
i 4 1 1
i 5 1 1
i 6 1 1
i 7 1 1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Prints:
Filling gSArr[] in instr 1 at init-time!
Printing gSArr[] in instr 2 at init-time:
[nudosc coudns dsocun ocsund osncdu ]
Printing gSArr[] in instr 3 at perf-time:
[nudosc coudns dsocun ocsund osncdu ]
Modifying gSArr[] in instr 4 at init-time!
Printing gSArr[] in instr 5 at init-time:
[ousndc uocdns sudocn usnocd ouncds ]
Modifying gSArr[] in instr 6 at k-cycle 1!
Printing gSArr[] in instr 7 at k-cycle 1:
[s < x + ! ]
Modifying gSArr[] in instr 6 at k-cycle 2!
Printing gSArr[] in instr 7 at k-cycle 2:
[P Z r u U ]
Modifying gSArr[] in instr 6 at k-cycle 3!
Printing gSArr[] in instr 7 at k-cycle 3:
[b K c " h ]
Arrays of Audio Signals
Collecting audio signals in an array simplifies working with multiple channels, as one of many possible cases of use. Here are two simple examples, one for local audio arrays and the other for global audio arrays.
EXAMPLE 03E05_Local_audio_array.csd
<CsoundSynthesizer>
<CsOptions>
-odac -d
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1
aArr[] init 2
a1 poscil .2, 400
a2 poscil .2, 500
kEnv transeg 1, p3, -3, 0
aArr[0] = a1 * kEnv
aArr[1] = a2 * kEnv
outch 1, aArr[0], 2, aArr[1]
endin
instr 2 ;to test identical names
aArr[] init 2
a1 poscil .2, 600
a2 poscil .2, 700
kEnv transeg 0, p3-p3/10, 3, 1, p3/10, -6, 0
aArr[0] = a1 * kEnv
aArr[1] = a2 * kEnv
outch 1, aArr[0], 2, aArr[1]
endin
</CsInstruments>
<CsScore>
i 1 0 3
i 2 0 3
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
EXAMPLE 03E06_Global_audio_array.csd
<CsoundSynthesizer>
<CsOptions>
-odac -d
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
gaArr[] init 2
instr 1 ; left channel
kEnv loopseg 0.5, 0, 0, 1,0.003, 1,0.0001, 0,0.9969
aSig pinkish kEnv
gaArr[0] = aSig
endin
instr 2 ; right channel
kEnv loopseg 0.5, 0, 0.5, 1,0.003, 1,0.0001, 0,0.9969
aSig pinkish kEnv
gaArr[1] = aSig
endin
instr 3 ; reverb
aInSigL = gaArr[0] / 3
aInSigR = gaArr[1] / 2
aRvbL,aRvbR reverbsc aInSigL, aInSigR, 0.88, 8000
gaArr[0] = gaArr[0] + aRvbL
gaArr[1] = gaArr[1] + aRvbR
outs gaArr[0]/4, gaArr[1]/4
gaArr[0] = 0
gaArr[1] = 0
endin
</CsInstruments>
<CsScore>
i 1 0 10
i 2 0 10
i 3 0 12
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz, using code by iain mccurdy
If you use diskin, the array is created automatically in the size which fits to the number of channels in the input file:
arr[] diskin "7chnls.aiff"
will create an audio array of size 7 according to the seven channel input file. Similarly, many opcodes with audio output can directly write to arrays, for instance vbap, the ambisonics opcodes bformenc1/bformdec1 or the array-based spectral opcodes.
More on Array Rates
Usually the first character of a variable name in Csound shows whether it is i-rate or k-rate or a-rate. But for arrays, we have actually two signifiers: the array variable name, and the index type. If both coincide, it is easy:
- i_array[i_index] reads and writes at i-time
- k_array[k_index] reads and writes at k-time
- a_array[a_index] reads and writes at a-time
But what to do if array type and index type do not coincide? In general, the index type will then determine whether the array is read or written only once (at init-time) or at each k-cycle. This is valid in particular for S_arrays (containing strings) and f_arrays (containing f-data). Other cases are:
- i_array[k_index] reads at k-time; writing is not possible (yields a runtime error)
- k_array[i_index] reads and writes at k-rate
- a_array[i_index] reads and writes at a-rate
For usual k-variables, you can get the value at init-time via the expression i(kVar), for instance:
instr 1
gkLine linseg 1, 1, 2
schedule 2, .5, 0
endin
instr 2
iLine = i(gkLine)
print iLine
endin
will print: iLine = 1.499.
This expression cannot be used for arrays:
kArray[] fillarray 1, 2, 3
iFirst = i(kArray[0])
print iFirst
will print: iFirst = 0.000, which is obviously not what could be expected. For this purpose, the i() expression can be used to pass the index as second argument:
kArray[] fillarray 1, 2, 3
iFirst = i(kArray, 0)
print iFirst
will print: iFirst = 1.000.
Naming Conventions
An array must be created (via init or fillarray) as kMyArrayName plus ending brackets. The brackets determine the dimensions of the array. So
kArr[] init 10
creates a one-dimensional array of length 10, whereas
kArr[][] init 10, 10
creates a two-dimensional array with 10 rows and 10 columns.
After the initialization of the array, referring to the array as a whole is done without any brackets. Brackets are only used if an element is indexed:
kArr[] init 10 ;with brackets because of initialization kLen = lenarray(kArr) ;without brackets kFirstEl = kArr[0] ;with brackets because of indexing
The same syntax is used for a simple copy via the '=' operator:
kArr1[] array 1, 2, 3, 4, 5 ;creates kArr1 kArr2[] = kArr1 ;creates kArr2 as copy of kArr1
Creating an Array
An array can currently be created by these methods: with the init opcode, with fillarray, with genarray, as a copy of an already existing array with the '=' operator (see above), or as a copy of a function table with copyf2array (see below).
init
The most general method, which works for arrays of any number of dimensions, is to use the init opcode. Here you define a specified space for the array:
kArr[] init 10 ;creates a one-dimensional array with length 10 kArr[][] init 10, 10 ;creates a two-dimensional array
fillarray
If you want to fill an array with distinct values, you can use the fillarray opcode. This line creates a vector with length 4 and puts in the numbers [1, 2, 3, 4]:
kArr[] fillarray 1, 2, 3, 4
You can also use this opcode for filling two-dimensional arrays.3 The example shows also the usage of the opcodes getrow and setrow to get or set one row of a two-dimensional array.
EXAMPLE 03E07_Fill_multidim_array.csd
<CsoundSynthesizer> <CsOptions> -nm0 </CsOptions> <CsInstruments> ksmps = 32
gk_2d_Arr[][] init 2,3 ;two lines, three columns
gk_2d_Arr fillarray 1,2,3,4,5,6
instr FirstContent
prints "First content of array gk_2d_arr:\n"
schedule "PrintContent", 0, 1
endin
instr ChangeRow
k_1d_Arr[] fillarray 7,8,9
gk_2d_Arr setrow k_1d_Arr, 0 ;change first row
prints "\nContent of gk_2d_Arr after having changed the first row:\n"
event "i", "PrintContent", 0, 1
turnoff
endin
instr GetRow
k_Row2[] getrow gk_2d_Arr, 1 ;second row as own array
prints "\nSecond row as own array:\n"
kColumn = 0
until kColumn == 3 do
printf "k_Row2[%d] = %d\n", kColumn+1, kColumn, k_Row2[kColumn]
kColumn += 1
od
turnoff
endin
instr PrintContent
kRow = 0
until kRow == 2 do
kColumn = 0
until kColumn == 3 do
printf "gk_2d_Arr[%d][%d] = %d\n", kColumn+1, kRow, kColumn, gk_2d_Arr[kRow][kColumn]
kColumn += 1
od
kRow += 1
od
turnoff
endin
</CsInstruments>
<CsScore>
i "FirstContent" 0 1
i "ChangeRow" .1 1
i "GetRow" .2 1 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
Prints:
First content of array gk_2d_arr:
gk_2d_Arr[0][0] = 1
gk_2d_Arr[0][1] = 2
gk_2d_Arr[0][2] = 3
gk_2d_Arr[1][0] = 4
gk_2d_Arr[1][1] = 5
gk_2d_Arr[1][2] = 6
Content of gk_2d_Arr after having changed the first row:
gk_2d_Arr[0][0] = 7
gk_2d_Arr[0][1] = 8
gk_2d_Arr[0][2] = 9
gk_2d_Arr[1][0] = 4
gk_2d_Arr[1][1] = 5
gk_2d_Arr[1][2] = 6
Second row as own array:
k_Row2[0] = 4
k_Row2[1] = 5
k_Row2[2] = 6
genarray
This opcode creates an array which is filled by a series of numbers from a starting value to an (included) ending value. Here are some examples:
iArr[] genarray 1, 5 ; creates i-array with [1, 2, 3, 4, 5] kArr[] genarray_i 1, 5 ; creates k-array at init-time with [1, 2, 3, 4, 5] iArr[] genarray -1, 1, 0.5 ; i-array with [-1, -0.5, 0, 0.5, 1] iArr[] genarray 1, -1, -0.5 ; [1, 0.5, 0, -0.5, -1] iArr[] genarray -1, 1, 0.6 ; [-1, -0.4, 0.2, 0.8]
Basic Operations: len, slice
The opcode lenarray reports the length of an i- or k-array. As with many opcodes now in Csound 6, it can be used either in the traditional way (Left-hand-side <- Opcode <- Right-hand-side), or as a function. The next example shows both usages, for i- and k-arrays. For multidimensional arrays, lenarray returns the length of the first dimension (instr 5).
EXAMPLE 03E08_lenarray.csd
<CsoundSynthesizer>
<CsOptions>
-nm0
</CsOptions>
<CsInstruments>
ksmps = 32
instr 1 ;simple i-rate example
iArr[] fillarray 1, 3, 5, 7, 9
iLen lenarray iArr
prints "Length of iArr = %d\n", iLen
endin
instr 2 ;simple k-rate example
kArr[] fillarray 2, 4, 6, 8
kLen lenarray kArr
printks "Length of kArr = %d\n", 0, kLen
turnoff
endin
instr 3 ;i-rate with functional syntax
iArr[] genarray 1, 9, 2
iIndx = 0
until iIndx == lenarray(iArr) do
prints "iArr[%d] = %d\n", iIndx, iArr[iIndx]
iIndx += 1
od
endin
instr 4 ;k-rate with functional syntax
kArr[] genarray_i -2, -8, -2
kIndx = 0
until kIndx == lenarray(kArr) do
printf "kArr[%d] = %d\n", kIndx+1, kIndx, kArr[kIndx]
kIndx += 1
od
turnoff
endin
instr 5 ;multi-dimensional arrays
kArr[][] init 9, 5
kArrr[][][] init 7, 9, 5
printks "lenarray(kArr) (2-dim) = %d\n", 0, lenarray(kArr)
printks "lenarray(kArrr) (3-dim) = %d\n", 0, lenarray(kArrr)
turnoff
endin
</CsInstruments>
<CsScore>
i 1 0 0
i 2 .1 .1
i 3 .2 0
i 4 .3 .1
i 5 .4 .1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Prints:
Length of iArr = 5
Length of kArr = 4
iArr[0] = 1
iArr[1] = 3
iArr[2] = 5
iArr[3] = 7
iArr[4] = 9
kArr[0] = -2
kArr[1] = -4
kArr[2] = -6
kArr[3] = -8
lenarray(kArr) (2-dim) = 9
lenarray(kArrr) (3-dim) = 7
The opcode slicearray takes a slice of a (one-dimensional) array:
kSlice[] slicearray kArr, iStart, iEnd [,kIncr]
returns a slice of kArr from index iStart to index iEnd (included). The increment defaults to 1, but can be set to other values for extracting the odd or even indices, for instance:
kArr[] fillarray 1, 2, 3, 4, 5, 6, 7, 8, 9 kSl1[] slicearray kArr, 0, 4 ;[1, 2, 3, 4, 5] kSl2[] slicearray kArr, 5, 8 ;[6, 7, 8, 9]
kSl3[] slicearray kArr, 0, 8, 2 ;[1, 3, 5, 7, 9]
kSl4[] slicearray kArr, 1, 8, 2 ;[2, 4, 6, 8]
EXAMPLE 03E09_slicearray.csd
<CsoundSynthesizer>
<CsOptions>
-n
</CsOptions>
<CsInstruments>
ksmps = 32
instr 1
;create and fill an array
kArr[] genarray_i 1, 9
;print the content (after csound 6.12, simply use printarray)
printf "%s", 1, "kArr = whole array\n"
kndx = 0
until kndx == lenarray(kArr) do
printf "kArr[%d] = %f\n", kndx+1, kndx, kArr[kndx]
kndx += 1
od
;make slices
kArr1[] slicearray kArr, 0, 4
kArr2[] slicearray kArr, 5, 8
kArr3[] slicearray kArr, 0, 8, 2
kArr4[] slicearray kArr, 1, 8, 2
;print the content
printf "%s", 1, "\nkArr1 = slice from index 0 to index 4\n"
kndx = 0
until kndx == lenarray:k(kArr1) do
printf "kArr1[%d] = %f\n", kndx+1, kndx, kArr1[kndx]
kndx += 1
od
printf "%s", 1, "\nkArr2 = slice from index 5 to index 8\n"
kndx = 0
until kndx == lenarray:k(kArr2) do
printf "kArr2[%d] = %f\n", kndx+1, kndx, kArr2[kndx]
kndx += 1
od
printf "%s", 1, "\nkArr3 = slice from index 0 to index 8 with increment 2\n"
kndx = 0
while kndx < lenarray:k(kArr3) do
printf "kArr3[%d] = %f\n", kndx+1, kndx, kArr3[kndx]
kndx += 1
od
printf "%s", 1, "\nkArr3 = slice from index 1 to index 8 with increment 2\n"
kndx = 0
while kndx < lenarray:k(kArr4) do
printf "kArr4[%d] = %f\n", kndx+1, kndx, kArr4[kndx]
kndx += 1
od
turnoff
endin
</CsInstruments>
<CsScore>
i 1 0 1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Copy Arrays from/to Tables
As function tables have been the classical way of working with arrays in Csound, switching between them and the new array facility in Csound is a basic operation. Copying data from a function table to a vector is done by copyf2array, whereas copya2ftab copies data from a vector to a function table:
copyf2array kArr, kfn ;from a function table to an array copya2ftab kArr, kfn ;from an array to a function table
The following presents a simple example of each operation.
EXAMPLE 03E10_copyf2array.csd
<CsoundSynthesizer>
<CsOptions>
-nm0
</CsOptions>
<CsInstruments>
ksmps = 32
;8 points sine wave function table
giSine ftgen 0, 0, 8, 10, 1
instr 1
;create array
kArr[] init 8
;copy table values in it
copyf2array kArr, giSine
;print values
kndx = 0
until kndx == lenarray(kArr) do
printf "kArr[%d] = %f\n", kndx+1, kndx, kArr[kndx]
kndx += 1
enduntil
;turn instrument off
turnoff
endin
</CsInstruments>
<CsScore>
i 1 0 0.1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
EXAMPLE 03E11_copya2ftab.csd
<CsoundSynthesizer>
<CsOptions>
-nm0
</CsOptions>
<CsInstruments>
ksmps = 32
;an 'empty' function table with 10 points
giTable ftgen 0, 0, -10, 2, 0
instr 1
;print inital values of giTable
puts "\nInitial table content:", 1
indx = 0
until indx == ftlen(giTable) do
iVal table indx, giTable
printf_i "Table index %d = %f\n", 1, indx, iVal
indx += 1
od
;create array with values 1..10
kArr[] genarray_i 1, 10
;print array values
printf "%s", 1, "\nArray content:\n"
kndx = 0
until kndx == lenarray(kArr) do
printf "kArr[%d] = %f\n", kndx+1, kndx, kArr[kndx]
kndx += 1
od
;copy array values to table
copya2ftab kArr, giTable
;print modified values of giTable
printf "%s", 1, "\nModified table content after copya2ftab:\n"
kndx = 0
until kndx == ftlen(giTable) do
kVal table kndx, giTable
printf "Table index %d = %f\n", kndx+1, kndx, kVal
kndx += 1
od
;turn instrument off
turnoff
endin
</CsInstruments>
<CsScore>
i 1 0 0.1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Copy Arrays from/to FFT Data
You can copy the data of an f-signal - which contains the results of a Fast Fourier Transform - into an array with the opcode pvs2array. The counterpart pvsfromarray copies the content of an array to a f-signal.
kFrame pvs2array kArr, fSigIn ;from f-signal fSig to array kArr fSigOut pvsfromarray kArr [,ihopsize, iwinsize, iwintype]
Some care is needed to use these opcodes correctly:
- The array kArr must be declared in advance to its usage in these opcodes, usually with init.
- The size of this array depends on the FFT size of the f-signal fSigIn. If the FFT size is N, the f-signal will contain N/2+1 amplitude-frequency pairs. For instance, if the FFT size is 1024, the FFT will write out 513 bins, each bin containing one value for amplitude and one value for frequency. So to store all these values, the array must have a size of 1026. In general, the size of kArr equals FFT-size plus two.
- The indices 0, 2, 4, ... of kArr will contain the amplitudes; the indices 1, 3, 5, ... will contain the frequencies of the bins of a specific frame.
- The number of this frame is reported in the kFrame output of pvs2array. By this parameter you know when pvs2array writes new values to the array kArr.
- On the way back, the FFT size of fSigOut, which is written by pvsfromarray, depends on the size of kArr. If the size of kArr is 1026, the FFT size will be 1024.
- The default value for ihopsize is 4 (= fftsize/4); the default value for inwinsize is the fftsize; and the default value for iwintype is 1, which means a hanning window.
Here is an example that implements a spectral high-pass filter. The f-signal is written to an array and the amplitudes of the first 40 bins are then zeroed.4 This is only done when a new frame writes its values to the array so as not to waste rendering power.
EXAMPLE 03E12_pvs_to_from_array.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
gifil ftgen 0, 0, 0, 1, "fox.wav", 0, 0, 1
instr 1
ifftsize = 2048 ;fft size set to pvstanal default
fsrc pvstanal 1, 1, 1, gifil ;create fsig stream from function table
kArr[] init ifftsize+2 ;create array for bin data
kflag pvs2array kArr, fsrc ;export data to array
;if kflag has reported a new write action ...
knewflag changed kflag
if knewflag == 1 then
; ... set amplitude of first 40 bins to zero:
kndx = 0 ;even array index = bin amplitude
kstep = 2 ;change only even indices
kmax = 80
loop:
kArr[kndx] = 0
loop_le kndx, kstep, kmax, loop
endif
fres pvsfromarray kArr ;read modified data back to fres
aout pvsynth fres ;and resynth
outs aout, aout
endin
</CsInstruments>
<CsScore>
i 1 0 2.7
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Basically, with the opcodes pvs2array and pvsfromarray, you have complete access to every operation in the spectral domain. You could re-write the existing pvs transformations, you could change them, but you can also simply use the spectral data to do anything with it. The next example looks for the most prominent amplitudes in a frame, and then triggers another instrument.
EXAMPLE 03E13_fft_peaks_arpegg.csd
<CsoundSynthesizer>
<CsOptions>
-odac -d -m128
; Example by Tarmo Johannes
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 4096, 10, 1
instr getPeaks
;generate signal to analyze
kfrcoef jspline 60, 0.1, 1 ; change the signal in time a bit for better testing
kharmcoef jspline 4, 0.1, 1
kmodcoef jspline 1, 0.1, 1
kenv linen 0.5, 0.05, p3, 0.05
asig foscil kenv, 300+kfrcoef, 1, 1+kmodcoef, 10, giSine
outs asig*0.05, asig*0.05 ; original sound in backround
;FFT analysis
ifftsize = 1024
ioverlap = ifftsize / 4
iwinsize = ifftsize
iwinshape = 1
fsig pvsanal asig, ifftsize, ioverlap, iwinsize, iwinshape
ithresh = 0.001 ; detect only peaks over this value
;FFT values to array
kFrames[] init iwinsize+2 ; declare array
kframe pvs2array kFrames, fsig ; even member = amp of one bin, odd = frequency
;detect peaks
kindex = 2 ; start checking from second bin
kcounter = 0
iMaxPeaks = 13 ; track up to iMaxPeaks peaks
ktrigger metro 1/2 ; check after every 2 seconds
if ktrigger == 1 then
loop:
; check with neigbouring amps - if higher or equal than previous amp
; and more than the coming one, must be peak.
if (kFrames[kindex-2]<=kFrames[kindex] &&
kFrames[kindex]>kFrames[kindex+2] &&
kFrames[kindex]>ithresh &&
kcounter<iMaxPeaks) then
kamp = kFrames[kindex]
kfreq = kFrames[kindex+1]
; play sounds with the amplitude and frequency of the peak as in arpeggio
event "i", "sound", kcounter*0.1, 1, kamp, kfreq
kcounter = kcounter+1
endif
loop_lt kindex, 2, ifftsize, loop
endif
endin
instr sound
iamp = p4
ifreq = p5
kenv adsr 0.1,0.1,0.5,p3/2
kndx line 5,p3,1
asig foscil iamp*kenv, ifreq,1,0.75,kndx,giSine
outs asig, asig
endin
</CsInstruments>
<CsScore>
i "getPeaks" 0 60
</CsScore>
</CsoundSynthesizer>
Other fft based opcodes which create or manipulate arrays can be found in the array-based spectral opcodes overview of the Csound Manual.
Math Operations
+, -, *, / on a Number
If the four basic math operators are used between an array and a scalar (number), the operation is applied to each element. The safest way to do this is to store the result in a new array:
kArr1[] fillarray 1, 2, 3 kArr2[] = kArr1 + 10 ;(kArr2 is now [11, 12, 13])
But you can also overwrite the first array, and use a C-style syntax for it. Here is an example for both ways.
EXAMPLE 03E14_array_scalar_math.csd
<CsoundSynthesizer>
<CsOptions>
-n -m128
</CsOptions>
<CsInstruments>
ksmps = 32
instr 1
;create array and fill with numbers 1..10
kArr1[] genarray_i 1, 10
;print content
printf "%s", 1, "\nInitial content:\n"
kndx = 0
until kndx == lenarray(kArr1) do
printf "kArr[%d] = %f\n", kndx+1, kndx, kArr1[kndx]
kndx += 1
od
;add 10
kArr2[] = kArr1 + 10
;print content
printf "%s", 1, "\nAfter adding 10:\n"
kndx = 0
until kndx == lenarray(kArr2) do
printf "kArr[%d] = %f\n", kndx+1, kndx, kArr2[kndx]
kndx += 1
od
;subtract 5
kArr3[] = kArr2 - 5
;print content
printf "%s", 1, "\nAfter subtracting 5:\n"
kndx = 0
until kndx == lenarray(kArr3) do
printf "kArr[%d] = %f\n", kndx+1, kndx, kArr3[kndx]
kndx += 1
od
;multiply by -1.5
kArr4[] = kArr3 * -1.5
;print content
printf "%s", 1, "\nAfter multiplying by -1.5:\n"
kndx = 0
until kndx == lenarray(kArr4) do
printf "kArr[%d] = %f\n", kndx+1, kndx, kArr4[kndx]
kndx += 1
od
;divide by -3/2
kArr5[] = kArr4 / -(3/2)
;print content
printf "%s", 1, "\nAfter dividing by -3/2:\n"
kndx = 0
until kndx == lenarray(kArr5) do
printf "kArr[%d] = %f\n", kndx+1, kndx, kArr5[kndx]
kndx += 1
od
;turnoff
turnoff
endin
instr 2
iArr[] genarray 1, 9
printarray iArr, "%.0f", "original array:"
iArr += 10
printarray iArr, "%.0f", "kArr += 10:"
iArr -= 10
printarray iArr, "%.0f", "kArr -= 10:"
iArr *= 10
printarray iArr, "%.0f", "kArr *= 10:"
iArr /= 10
printarray iArr, "%.0f", "kArr /= 10:"
endin
</CsInstruments>
<CsScore>
i 1 0 .1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Prints:
Initial content:
kArr[0] = 1.000000
kArr[1] = 2.000000
kArr[2] = 3.000000
kArr[3] = 4.000000
kArr[4] = 5.000000
kArr[5] = 6.000000
kArr[6] = 7.000000
kArr[7] = 8.000000
kArr[8] = 9.000000
kArr[9] = 10.000000
After adding 10:
kArr[0] = 11.000000
kArr[1] = 12.000000
kArr[2] = 13.000000
kArr[3] = 14.000000
kArr[4] = 15.000000
kArr[5] = 16.000000
kArr[6] = 17.000000
kArr[7] = 18.000000
kArr[8] = 19.000000
kArr[9] = 20.000000
After subtracting 5:
kArr[0] = 6.000000
kArr[1] = 7.000000
kArr[2] = 8.000000
kArr[3] = 9.000000
kArr[4] = 10.000000
kArr[5] = 11.000000
kArr[6] = 12.000000
kArr[7] = 13.000000
kArr[8] = 14.000000
kArr[9] = 15.000000
After multiplying by -1.5:
kArr[0] = -9.000000
kArr[1] = -10.500000
kArr[2] = -12.000000
kArr[3] = -13.500000
kArr[4] = -15.000000
kArr[5] = -16.500000
kArr[6] = -18.000000
kArr[7] = -19.500000
kArr[8] = -21.000000
kArr[9] = -22.500000
After dividing by -3/2:
kArr[0] = 6.000000
kArr[1] = 7.000000
kArr[2] = 8.000000
kArr[3] = 9.000000
kArr[4] = 10.000000
kArr[5] = 11.000000
kArr[6] = 12.000000
kArr[7] = 13.000000
kArr[8] = 14.000000
kArr[9] = 15.000000
original array:
1 2 3 4 5 6 7 8 9
kArr += 10:
11 12 13 14 15 16 17 18 19
kArr -= 10:
1 2 3 4 5 6 7 8 9
kArr *= 10:
10 20 30 40 50 60 70 80 90
kArr /= 10:
1 2 3 4 5 6 7 8 9 0
+, -, *, / on a Second Array
If the four basic math operators are used between two arrays, their operation is applied element by element. The result can be easily stored in a new array:
kArr1[] fillarray 1, 2, 3 kArr2[] fillarray 10, 20, 30 kArr3[] = kArr1 + kArr2 ;(kArr3 is now [11, 22, 33])
Here is an example of array-array operations.
EXAMPLE 03E15_array_array_math.csd
<CsoundSynthesizer>
<CsOptions>
-n -m128
</CsOptions>
<CsInstruments>
ksmps = 32
instr 1
;create array and fill with numbers 1..10 resp .1..1
kArr1[] fillarray 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
kArr2[] fillarray 1, 2, 3, 5, 8, 13, 21, 34, 55, 89
;print contents
printf "%s", 1, "\nkArr1:\n"
kndx = 0
until kndx == lenarray(kArr1) do
printf "kArr1[%d] = %f\n", kndx+1, kndx, kArr1[kndx]
kndx += 1
od
printf "%s", 1, "\nkArr2:\n"
kndx = 0
until kndx == lenarray(kArr2) do
printf "kArr2[%d] = %f\n", kndx+1, kndx, kArr2[kndx]
kndx += 1
od
;add arrays
kArr3[] = kArr1 + kArr2
;print content
printf "%s", 1, "\nkArr1 + kArr2:\n"
kndx = 0
until kndx == lenarray(kArr3) do
printf "kArr3[%d] = %f\n", kndx+1, kndx, kArr3[kndx]
kndx += 1
od
;subtract arrays
kArr4[] = kArr1 - kArr2
;print content
printf "%s", 1, "\nkArr1 - kArr2:\n"
kndx = 0
until kndx == lenarray(kArr4) do
printf "kArr4[%d] = %f\n", kndx+1, kndx, kArr4[kndx]
kndx += 1
od
;multiply arrays
kArr5[] = kArr1 * kArr2
;print content
printf "%s", 1, "\nkArr1 * kArr2:\n"
kndx = 0
until kndx == lenarray(kArr5) do
printf "kArr5[%d] = %f\n", kndx+1, kndx, kArr5[kndx]
kndx += 1
od
;divide arrays
kArr6[] = kArr1 / kArr2
;print content
printf "%s", 1, "\nkArr1 / kArr2:\n"
kndx = 0
until kndx == lenarray(kArr6) do
printf "kArr5[%d] = %f\n", kndx+1, kndx, kArr6[kndx]
kndx += 1
od
;turnoff
turnoff
endin
</CsInstruments>
<CsScore>
i 1 0 .1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
min, max, sum, scale
minarray and maxarray return the smallest / largest value in an array, and optionally its index:
kMin [,kMinIndx] minarray kArr kMax [,kMaxIndx] maxarray kArr
Here is a simple example of these operations:
EXAMPLE 03E16_min_max_array.csd
<CsoundSynthesizer>
<CsOptions>
-nm0
</CsOptions>
<CsInstruments>
ksmps = 32
seed 0
instr 1
;create an array with 10 elements
kArr[] init 10
;fill in random numbers and print them out
kIndx = 0
until kIndx == 10 do
kNum random -100, 100
kArr[kIndx] = kNum
printf "kArr[%d] = %10f\n", kIndx+1, kIndx, kNum
kIndx += 1
od
;investigate minimum and maximum number and print them out
kMin, kMinIndx minarray kArr
kMax, kMaxIndx maxarray kArr
printf "Minimum of kArr = %f at index %d\n", kIndx+1, kMin, kMinIndx
printf "Maximum of kArr = %f at index %d\n\n", kIndx+1, kMax, kMaxIndx
turnoff
endin
</CsInstruments>
<CsScore>
i1 0 0.1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
This would create a different output each time you run it; for instance:
kArr[0] = -2.071383
kArr[1] = 97.150272
kArr[2] = 21.187835
kArr[3] = 72.199983
kArr[4] = -64.908241
kArr[5] = -7.276434
kArr[6] = -51.368650
kArr[7] = 41.324552
kArr[8] = -8.483235
kArr[9] = 77.560219
Minimum of kArr = -64.908241 at index 4
Maximum of kArr = 97.150272 at index 1
sumarray simply returns the sum of all values in an (numerical) array. Here is a simple example:
EXAMPLE 03E17_sumarray.csd
<CsoundSynthesizer>
<CsOptions>
-nm0
</CsOptions>
<CsInstruments>
ksmps = 32
seed 0
instr 1
;create an array with 10 elements
kArr[] init 10
;fill in random numbers and print them out
kIndx = 0
until kIndx == 10 do
kNum random 0, 10
kArr[kIndx] = kNum
printf "kArr[%d] = %10f\n", kIndx+1, kIndx, kNum
kIndx += 1
od
;calculate sum of all values and print it out
kSum sumarray kArr
printf "Sum of all values in kArr = %f\n", kIndx+1, kSum
turnoff
endin
</CsInstruments>
<CsScore>
i1 0 0.1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Finally, scalearray scales the values of a given numerical array between a minimum and a maximum value. These lines ...
kArr[] fillarray 1, 3, 9, 5, 6
scalearray kArr, 1, 3
... change kArr from [1, 3, 9, 5, 6] to [1, 1.5, 3, 2, 2.25]. Here is a simple example:
EXAMPLE 03E18_scalearray.csd
<CsoundSynthesizer>
<CsOptions>
-nm0
</CsOptions>
<CsInstruments>
ksmps = 32
seed 0
instr 1
;create an array with 10 elements
kArr[] init 10
;fill in random numbers and print them out
printks "kArr in maximum range 0..100:\n", 0
kIndx = 0
until kIndx == 10 do
kNum random 0, 100
kArr[kIndx] = kNum
printf "kArr[%d] = %10f\n", kIndx+1, kIndx, kNum
kIndx += 1
od
;scale numbers 0...1 and print them out again
scalearray kArr, 0, 1
kIndx = 0
printks "kArr in range 0..1\n", 0
until kIndx == 10 do
printf "kArr[%d] = %10f\n", kIndx+1, kIndx, kArr[kIndx]
kIndx += 1
od
turnoff
endin
</CsInstruments>
<CsScore>
i1 0 0.1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
One possible output:
kArr in maximum range 0..100:
kArr[0] = 93.898027
kArr[1] = 98.554934
kArr[2] = 37.244273
kArr[3] = 58.581820
kArr[4] = 71.195263
kArr[5] = 11.948356
kArr[6] = 3.493777
kArr[7] = 13.688537
kArr[8] = 24.875835
kArr[9] = 52.205258
kArr in range 0..1
kArr[0] = 0.951011
kArr[1] = 1.000000
kArr[2] = 0.355040
kArr[3] = 0.579501
kArr[4] = 0.712189
kArr[5] = 0.088938
kArr[6] = 0.000000
kArr[7] = 0.107244
kArr[8] = 0.224929
kArr[9] = 0.512423
Function Mapping on an Array: maparray
maparray applies the function "fun" (which needs to have one input and one output argument) to each element of the vector kArrSrc and stores the result in kArrRes (which needs to have been created previously):
kArrRes maparray kArrSrc, "fun"
Possible functions are for instance abs, ceil, exp, floor, frac, int, log, log10, round, sqrt. The following example applies different functions sequentially to the source array:
EXAMPLE 03E19_maparray.csd
<CsoundSynthesizer>
<CsOptions>
-nm0
</CsOptions>
<CsInstruments>
ksmps = 32
instr 1
;create an array and fill with numbers
kArrSrc[] array 1.01, 2.02, 3.03, 4.05, 5.08, 6.13, 7.21
;print source array
printf "%s", 1, "\nSource array:\n"
kndx = 0
until kndx == lenarray(kArrSrc) do
printf "kArrSrc[%d] = %f\n", kndx+1, kndx, kArrSrc[kndx]
kndx += 1
od
;create an empty array for the results
kArrRes[] init 7
;apply the sqrt() function to each element
kArrRes maparray kArrSrc, "sqrt"
;print the result
printf "%s", 1, "\nResult after applying sqrt() to source array\n"
kndx = 0
until kndx == lenarray(kArrRes) do
printf "kArrRes[%d] = %f\n", kndx+1, kndx, kArrRes[kndx]
kndx += 1
od
;apply the log() function to each element
kArrRes maparray kArrSrc, "log"
;print the result
printf "%s", 1, "\nResult after applying log() to source array\n"
kndx = 0
until kndx == lenarray(kArrRes) do
printf "kArrRes[%d] = %f\n", kndx+1, kndx, kArrRes[kndx]
kndx += 1
od
;apply the int() function to each element
kArrRes maparray kArrSrc, "int"
;print the result
printf "%s", 1, "\nResult after applying int() to source array\n"
kndx = 0
until kndx == lenarray(kArrRes) do
printf "kArrRes[%d] = %f\n", kndx+1, kndx, kArrRes[kndx]
kndx += 1
od
;apply the frac() function to each element
kArrRes maparray kArrSrc, "frac"
;print the result
printf "%s", 1, "\nResult after applying frac() to source array\n"
kndx = 0
until kndx == lenarray(kArrRes) do
printf "kArrRes[%d] = %f\n", kndx+1, kndx, kArrRes[kndx]
kndx += 1
od
;turn instrument instance off
turnoff
endin
</CsInstruments>
<CsScore>
i 1 0 0.1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Prints:
Source array:
kArrSrc[0] = 1.010000
kArrSrc[1] = 2.020000
kArrSrc[2] = 3.030000
kArrSrc[3] = 4.050000
kArrSrc[4] = 5.080000
kArrSrc[5] = 6.130000
kArrSrc[6] = 7.210000
Result after applying sqrt() to source array
kArrRes[0] = 1.004988
kArrRes[1] = 1.421267
kArrRes[2] = 1.740690
kArrRes[3] = 2.012461
kArrRes[4] = 2.253886
kArrRes[5] = 2.475884
kArrRes[6] = 2.685144
Result after applying log() to source array
kArrRes[0] = 0.009950
kArrRes[1] = 0.703098
kArrRes[2] = 1.108563
kArrRes[3] = 1.398717
kArrRes[4] = 1.625311
kArrRes[5] = 1.813195
kArrRes[6] = 1.975469
Result after applying int() to source array
kArrRes[0] = 1.000000
kArrRes[1] = 2.000000
kArrRes[2] = 3.000000
kArrRes[3] = 4.000000
kArrRes[4] = 5.000000
kArrRes[5] = 6.000000
kArrRes[6] = 7.000000
Result after applying frac() to source array
kArrRes[0] = 0.010000
kArrRes[1] = 0.020000
kArrRes[2] = 0.030000
kArrRes[3] = 0.050000
kArrRes[4] = 0.080000
kArrRes[5] = 0.130000
kArrRes[6] = 0.210000
Arrays in UDOs
The dimension of an input array must be declared in two places:
- as k[] or k[][] in the type input list
- as kName[], kName[][] etc in the xin list.
For Instance:
opcode FirstEl, k, k[]
;returns the first element of vector kArr
kArr[] xin
xout kArr[0]
endop
This is a simple example using this code:
EXAMPLE 03E20_array_UDO.csd
<CsoundSynthesizer>
<CsOptions>
-nm128
</CsOptions>
<CsInstruments>
ksmps = 32
opcode FirstEl, k, k[]
;returns the first element of vector kArr
kArr[] xin
xout kArr[0]
endop
instr 1
kArr[] array 6, 3, 9, 5, 1
kFirst FirstEl kArr
printf "kFirst = %d\n", 1, kFirst
turnoff
endin
</CsInstruments>
<CsScore>
i 1 0 .1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
As there is no built-in opcode for printing the contents of an array, it is a good task for an UDO. Let us finish with an example that does just this:
EXAMPLE 03E21_print_array.csd
<CsoundSynthesizer>
<CsOptions>
-n -m0
</CsOptions>
<CsInstruments>
ksmps = 32
seed 0
opcode PrtArr1k, 0, k[]POVVO
kArr[], ktrig, kstart, kend, kprec, kppr xin
kprint init 0
kndx init 0
if ktrig > 0 then
kppr = (kppr == 0 ? 10 : kppr)
kend = (kend == -1 || kend == .5 ? lenarray(kArr) : kend)
kprec = (kprec == -1 || kprec == .5 ? 3 : kprec)
kndx = kstart
Sformat sprintfk "%%%d.%df, ", kprec+3, kprec
Sdump sprintfk "%s", "["
loop:
Snew sprintfk Sformat, kArr[kndx]
Sdump strcatk Sdump, Snew
kmod = (kndx+1-kstart) % kppr
if kmod == 0 && kndx != kend-1 then
printf "%s\n", kprint+1, Sdump
Sdump strcpyk " "
endif
kprint = kprint + 1
loop_lt kndx, 1, kend, loop
klen strlenk Sdump
Slast strsubk Sdump, 0, klen-2
printf "%s]\n", kprint+1, Slast
endif
endop
instr SimplePrinting
kArr[] fillarray 1, 2, 3, 4, 5, 6, 7
kPrint metro 1
prints "\nSimple Printing with defaults, once a second:\n"
PrtArr1k kArr, kPrint
endin
instr EatTheHead
kArr[] fillarray 1, 2, 3, 4, 5, 6, 7
kPrint metro 1
kStart init 0
prints "\nChanging the start index:\n"
if kPrint == 1 then
PrtArr1k kArr, 1, kStart
kStart += 1
endif
endin
instr EatTheTail
kArr[] fillarray 1, 2, 3, 4, 5, 6, 7
kPrint metro 1
kEnd init 7
prints "\nChanging the end index:\n"
if kPrint == 1 then
PrtArr1k kArr, 1, 0, kEnd
kEnd -= 1
endif
endin
instr PrintFormatted
;create an array with 24 elements
kArr[] init 24
;fill with random values
kndx = 0
until kndx == lenarray(kArr) do
kArr[kndx] rnd31 10, 0
kndx += 1
od
;print
prints "\nPrinting with precision=5 and 4 elements per row:\n"
PrtArr1k kArr, 1, 0, -1, 5, 4
printks "\n", 0
;turnoff after first k-cycle
turnoff
endin
</CsInstruments>
<CsScore>
i "SimplePrinting" 0 5
i "EatTheHead" 6 5
i "EatTheTail" 12 5
i "PrintFormatted" 18 1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Prints:
Simple Printing with defaults, once a second:
[ 1.000, 2.000, 3.000, 4.000, 5.000, 6.000, 7.000]
[ 1.000, 2.000, 3.000, 4.000, 5.000, 6.000, 7.000]
[ 1.000, 2.000, 3.000, 4.000, 5.000, 6.000, 7.000]
[ 1.000, 2.000, 3.000, 4.000, 5.000, 6.000, 7.000]
[ 1.000, 2.000, 3.000, 4.000, 5.000, 6.000, 7.000]
Changing the start index:
[ 1.000, 2.000, 3.000, 4.000, 5.000, 6.000, 7.000]
[ 2.000, 3.000, 4.000, 5.000, 6.000, 7.000]
[ 3.000, 4.000, 5.000, 6.000, 7.000]
[ 4.000, 5.000, 6.000, 7.000]
[ 5.000, 6.000, 7.000]
Changing the end index:
[ 1.000, 2.000, 3.000, 4.000, 5.000, 6.000, 7.000]
[ 1.000, 2.000, 3.000, 4.000, 5.000, 6.000]
[ 1.000, 2.000, 3.000, 4.000, 5.000]
[ 1.000, 2.000, 3.000, 4.000]
[ 1.000, 2.000, 3.000]
Printing with precision=5 and 4 elements per row:
[-6.02002, 1.55606, -7.25789, -3.43802,
-2.86539, 1.35237, 9.26686, 8.13951,
0.68799, 3.02332, -7.03470, 7.87381,
-4.86597, -2.42907, -5.44999, 2.07420,
1.00121, 7.33340, -7.53952, 3.23020,
9.93770, 2.84713, -8.23949, -1.12326]
- You cannot currently have a mixture of numbers and strings in an array, but you can convert a string to a number with the strtod opcode.^
- Actually, fillarray is supposed to work for one dimension. It will probably work on two dimensions, but not at three or more.^
- As sample rate is here 44100, and fftsize is 2048, each bin has a frequency range of 44100 / 2048 = 21.533 Hz. Bin 0 looks for frequencies around 0 Hz, bin 1 for frequencies around 21.533 Hz, bin 2 around 43.066 Hz, and so on. So setting the first 40 bin amplitudes to 0 means that no frequencies will be resynthesized which are lower than bin 40 which is centered at 40 * 21.533 = 861.328 Hz. ^
LIVE EVENTS
The basic concept of Csound from the early days of the program is still valid and useful because it is a musically familiar one: you create a set of instruments and instruct them to play at various times. These calls of instrument instances, and their execution, are called "instrument events".
Whenever any Csound code is executed, it has to be compiled first. Since Csound6, you can change the code of any running Csound instance, and recompile it on the fly. There are basically two opcodes for this "live coding": compileorc re-compiles any existing orc file, whereas compilestr compiles any string. At the end of this chapter, we will present some simple examples for both methods, followed by a description how to re-compile code on the fly in CsoundQt.
The scheme of instruments and events can be instigated in a number of ways. In the classical approach you think of an "orchestra" with a number of musicians playing from a "score", but you can also trigger instruments using any kind of live input: from MIDI, from OSC, from the command line, from a GUI (such as Csound's FLTK widgets or CsoundQt's widgets), from the API (also used in CsoundQt's Live Event Sheet). Or you can create a kind of "master instrument", which is always on, and triggers other instruments using opcodes designed for this task, perhaps under certain conditions: if the live audio input from a singer has been detected to have a base frequency greater than 1043 Hz, then start an instrument which plays a soundfile of broken glass...
Order of Execution Revisited
Whatever you do in Csound with instrument events, you must bear in mind the order of execution that has been explained in the first chapter of this section about the Initialization and Performance Pass: instruments are executed one by one, both in the initialization pass and in each control cycle, and the order is determined by the instrument number.
It is worth to have a closer look to what is happening exactly in time if you trigger an instrument from inside another instrument. The first example shows the result when instrument 2 triggers instrument 1 and instrument 3 at init-time.
EXAMPLE 03F01_OrderOfExc_event_i.csd
<CsoundSynthesizer> <CsOptions> -nm0 </CsOptions> <CsInstruments> sr = 44100 ksmps = 441 instr 1 kCycle timek prints "Instrument 1 is here at initialization.\n" printks "Instrument 1: kCycle = %d\n", 0, kCycle endin instr 2 kCycle timek prints " Instrument 2 is here at initialization.\n" printks " Instrument 2: kCycle = %d\n", 0, kCycle event_i "i", 3, 0, .02 event_i "i", 1, 0, .02 endin instr 3 kCycle timek prints " Instrument 3 is here at initialization.\n" printks " Instrument 3: kCycle = %d\n", 0, kCycle endin </CsInstruments> <CsScore> i 2 0 .02 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
This is the output:
Instrument 2 is here at initialization.
Instrument 3 is here at initialization.
Instrument 1 is here at initialization.
Instrument 1: kCycle = 1
Instrument 2: kCycle = 1
Instrument 3: kCycle = 1
Instrument 1: kCycle = 2
Instrument 2: kCycle = 2
Instrument 3: kCycle = 2
Instrument 2 is the first one to initialize, because it is the only one which is called by the score. Then instrument 3 is initialized, because it is called first by instrument 2. The last one is instrument 1. All this is done before the actual performance begins. In the performance itself, starting from the first control cycle, all instruments are executed by their order.
Let us compare now what is happening when instrument 2 calls instrument 1 and 3 during the performance (= at k-time):
EXAMPLE 03F02_OrderOfExc_event_k.csd
<CsoundSynthesizer> <CsOptions> -nm0 </CsOptions> <CsInstruments> sr = 44100 ksmps = 441 0dbfs = 1 nchnls = 1 instr 1 kCycle timek prints "Instrument 1 is here at initialization.\n" printks "Instrument 1: kCycle = %d\n", 0, kCycle endin instr 2 kCycle timek prints " Instrument 2 is here at initialization.\n" printks " Instrument 2: kCycle = %d\n", 0, kCycle if kCycle == 1 then event "i", 3, 0, .02 event "i", 1, 0, .02 endif printks " Instrument 2: still in kCycle = %d\n", 0, kCycle endin instr 3 kCycle timek prints " Instrument 3 is here at initialization.\n" printks " Instrument 3: kCycle = %d\n", 0, kCycle endin instr 4 kCycle timek prints " Instrument 4 is here at initialization.\n" printks " Instrument 4: kCycle = %d\n", 0, kCycle endin </CsInstruments> <CsScore> i 4 0 .02 i 2 0 .02 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
This is the output:
Instrument 2 is here at initialization.
Instrument 4 is here at initialization.
Instrument 2: kCycle = 1
Instrument 2: still in kCycle = 1
Instrument 4: kCycle = 1
Instrument 3 is here at initialization.
Instrument 1 is here at initialization.
Instrument 1: kCycle = 2
Instrument 2: kCycle = 2
Instrument 2: still in kCycle = 2
Instrument 3: kCycle = 2
Instrument 4: kCycle = 2
Instrument 2 starts with its init-pass, and then instrument 4 is initialized. As you see, the reverse order of the scorelines has no effect; the instruments which start at the same time are executed in ascending order, depending on their numbers.
In this first cycle, instrument 2 calls instrument 3 and 1. As you see by the output of instrument 4, the whole control cycle is finished first, before instrument 3 and 1 (in this order) are initialized.1 These both instruments start their performance in cycle number two, where they find themselves in the usual order: instrument 1 before instrument 2, then instrument 3 before instrument 4.
Usually you will not need to know all of this with such precise timing. But in case you experience any problems, a clearer awareness of the process may help.
Instrument Events From The Score
This is the classical way of triggering instrument events: you write a list in the score section of a .csd file. Each line which begins with an "i", is an instrument event. As this is very simple, and examples can be found easily, let us focus instead on some additional features which can be useful when you work in this way. Documentation for these features can be found in the Score Statements section of the Canonical Csound Reference Manual. Here are some examples:
EXAMPLE 03F03_Score_tricks.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giWav ftgen 0, 0, 2^10, 10, 1, .5, .3, .1
instr 1
kFadout init 1
krel release ;returns "1" if last k-cycle
if krel == 1 && p3 < 0 then ;if so, and negative p3:
xtratim .5 ;give 0.5 extra seconds
kFadout linseg 1, .5, 0 ;and make fade out
endif
kEnv linseg 0, .01, p4, abs(p3)-.1, p4, .09, 0; normal fade out
aSig poscil kEnv*kFadout, p5, giWav
outs aSig, aSig
endin
</CsInstruments>
<CsScore>
t 0 120 ;set tempo to 120 beats per minute
i 1 0 1 .2 400 ;play instr 1 for one second
i 1 2 -10 .5 500 ;play instr 1 indefinetely (negative p3)
i -1 5 0 ;turn it off (negative p1)
; -- turn on instance 1 of instr 1 one sec after the previous start
i 1.1 ^+1 -10 .2 600
i 1.2 ^+2 -10 .2 700 ;another instance of instr 1
i -1.2 ^+2 0 ;turn off 1.2
; -- turn off 1.1 (dot = same as the same p-field above)
i -1.1 ^+1 .
s ;end of a section, so time begins from new at zero
i 1 1 1 .2 800
r 5 ;repeats the following line (until the next "s")
i 1 .25 .25 .2 900
s
v 2 ;lets time be double as long
i 1 0 2 .2 1000
i 1 1 1 .2 1100
s
v 0.5 ;lets time be half as long
i 1 0 2 .2 1200
i 1 1 1 .2 1300
s ;time is normal now again
i 1 0 2 .2 1000
i 1 1 1 .2 900
s
; -- make a score loop (4 times) with the variable "LOOP"
{4 LOOP
i 1 [0 + 4 * $LOOP.] 3 .2 [1200 - $LOOP. * 100]
i 1 [1 + 4 * $LOOP.] 2 . [1200 - $LOOP. * 200]
i 1 [2 + 4 * $LOOP.] 1 . [1200 - $LOOP. * 300]
}
e
</CsScore>
</CsoundSynthesizer>
Triggering an instrument with an indefinite duration by setting p3 to any negative value, and stopping it by a negative p1 value, can be an important feature for live events. If you turn instruments off in this way you may have to add a fade out segment. One method of doing this is shown in the instrument above with a combination of the release and the xtratim opcodes. Also note that you can start and stop certain instances of an instrument with a floating point number as p1.
Using MIDI Note-On Events
Csound has a particular feature which makes it very simple to trigger instrument events from a MIDI keyboard. Each MIDI Note-On event can trigger an instrument, and the related Note-Off event of the same key stops the related instrument instance. This is explained more in detail in the chapter Triggering Instrument Instances in the MIDI section of this manual. Here, just a small example is shown. Simply connect your MIDI keyboard and it should work.
EXAMPLE 03F04_Midi_triggered_events.csd
<CsoundSynthesizer>
<CsOptions>
-Ma -odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
massign 0, 1; assigns all midi channels to instr 1
instr 1
iFreq cpsmidi ;gets frequency of a pressed key
iAmp ampmidi 8 ;gets amplitude and scales 0-8
iRatio random .9, 1.1 ;ratio randomly between 0.9 and 1.1
aTone foscili .1, iFreq, 1, iRatio/5, iAmp+1, giSine ;fm
aEnv linenr aTone, 0, .01, .01 ; avoiding clicks at the note-end
outs aEnv, aEnv
endin
</CsInstruments>
<CsScore>
f 0 36000; play for 10 hours
e
</CsScore>
</CsoundSynthesizer>
Using Widgets
If you want to trigger an instrument event in realtime with a Graphical User Interface, it is usually a "Button" widget which will do this job. We will see here a simple example; first implemented using Csound's FLTK widgets, and then using CsoundQt's widgets.
FLTK Button
This is a very simple example demonstrating how to trigger an instrument using an FLTK button. A more extended example can be found here.
EXAMPLE 03F05_FLTK_triggered_events.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
; -- create a FLTK panel --
FLpanel "Trigger By FLTK Button", 300, 100, 100, 100
; -- trigger instr 1 (equivalent to the score line "i 1 0 1")k1, ih1 FLbutton "Push me!", 0, 0, 1, 150, 40, 10, 25, 0, 1, 0, 1
; -- trigger instr 2
k2, ih2 FLbutton "Quit", 0, 0, 1, 80, 40, 200, 25, 0, 2, 0, 1
FLpanelEnd; end of the FLTK panel section
FLrun ; run FLTK
seed 0; random seed different each time
instr 1
idur random .5, 3; recalculate instrument duration
p3 = idur; reset instrument duration
ioct random 8, 11; random values between 8th and 11th octave
idb random -18, -6; random values between -6 and -18 dB
aSig poscil ampdb(idb), cpsoct(ioct)
aEnv transeg 1, p3, -10, 0
outs aSig*aEnv, aSig*aEnv
endin
instr 2
exitnow
endin
</CsInstruments>
<CsScore>
f 0 36000
e
</CsScore>
</CsoundSynthesizer>
Note that in this example the duration of an instrument event is recalculated when the instrument is initialised. This is done using the statement "p3 = i...". This can be a useful technique if you want the duration that an instrument plays for to be different each time it is called. In this example duration is the result of a random function'. The duration defined by the FLTK button will be overwritten by any other calculation within the instrument itself at i-time.
CsoundQt Button
In CsoundQt, a button can be created easily from the submenu in a widget panel:
In the Properties Dialog of the button widget, make sure you have selected "event" as Type. Insert a Channel name, and at the bottom type in the event you want to trigger - as you would if writing a line in the score.
In your Csound code, you need nothing more than the instrument you want to trigger:
For more information about CsoundQt, read the CsoundQt chapter in the 'Frontends' section of this manual.
Using A Realtime Score
Command Line With The -L stdin Option
If you use any .csd with the option "-L stdin" (and the -odac option for realtime output), you can type any score line in realtime (sorry, this does not work for Windows). For instance, save this .csd anywhere and run it from the command line:
EXAMPLE 03F06_Commandline_rt_events.csd
<CsoundSynthesizer>
<CsOptions>
-L stdin -odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0; random seed different each time
instr 1
idur random .5, 3; calculate instrument duration
p3 = idur; reset instrument duration
ioct random 8, 11; random values between 8th and 11th octave
idb random -18, -6; random values between -6 and -18 dB
aSig oscils ampdb(idb), cpsoct(ioct), 0
aEnv transeg 1, p3, -10, 0
outs aSig*aEnv, aSig*aEnv
endin
</CsInstruments>
<CsScore>
f 0 36000
e
</CsScore>
</CsoundSynthesizer>
If you run it by typing and returning a command line like this ...

... you should get a prompt at the end of the Csound messages:
If you now type the line "i 1 0 1" and press return, you should hear that instrument 1 has been executed. After three times your messages may look like this:
CsoundQt's Live Event Sheet
In general, this is the method that CsoundQt uses and it is made available to the user in a flexible environment called the Live Event Sheet. Have a look in the CsoundQt frontend to see more of the possibilities of "firing" live instrument events using the Live Event Sheet.2
By Conditions
We have discussed first the classical method of triggering instrument events from the score section of a .csd file, then we went on to look at different methods of triggering real time events using MIDI, by using widgets, and by using score lines inserted live. We will now look at the Csound orchestra itself and to some methods by which an instrument can internally trigger another instrument. The pattern of triggering could be governed by conditionals, or by different kinds of loops. As this "master" instrument can itself be triggered by a realtime event, you have unlimited options available for combining the different methods.
Let's start with conditionals. If we have a realtime input, we may want to define a threshold, and trigger an event
- if we cross the threshold from below to above;
- if we cross the threshold from above to below.
In Csound, this could be implemented using an orchestra of three instruments. The first instrument is the master instrument. It receives the input signal and investigates whether that signal is crossing the threshold and if it does whether it is crossing from low to high or from high to low. If it crosses the threshold from low ot high the second instrument is triggered, if it crosses from high to low the third instrument is triggered.
EXAMPLE 03F07_Event_by_condition.csd
<CsoundSynthesizer>
<CsOptions>
-iadc -odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0; random seed different each time
instr 1; master instrument
ichoose = p4; 1 = real time audio, 2 = random amplitude movement
ithresh = -12; threshold in dB
kstat init 1; 1 = under the threshold, 2 = over the threshold
;;CHOOSE INPUT SIGNAL
if ichoose == 1 then
ain inch 1
else
kdB randomi -18, -6, 1
ain pinkish ampdb(kdB)
endif
;;MEASURE AMPLITUDE AND TRIGGER SUBINSTRUMENTS IF THRESHOLD IS CROSSED
afoll follow ain, .1; measure mean amplitude each 1/10 second
kfoll downsamp afoll
if kstat == 1 && dbamp(kfoll) > ithresh then; transition down->up
event "i", 2, 0, 1; call instr 2
printks "Amplitude = %.3f dB%n", 0, dbamp(kfoll)
kstat = 2; change status to "up"
elseif kstat == 2 && dbamp(kfoll) < ithresh then; transition up->down
event "i", 3, 0, 1; call instr 3
printks "Amplitude = %.3f dB%n", 0, dbamp(kfoll)
kstat = 1; change status to "down"
endif
endin
instr 2; triggered if threshold has been crossed from down to up
asig poscil .2, 500
aenv transeg 1, p3, -10, 0
outs asig*aenv, asig*aenv
endin
instr 3; triggered if threshold has been crossed from up to down
asig poscil .2, 400
aenv transeg 1, p3, -10, 0
outs asig*aenv, asig*aenv
endin
</CsInstruments>
<CsScore>
i 1 0 1000 2 ;change p4 to "1" for live input
e
</CsScore>
</CsoundSynthesizer>
Using i-Rate Loops For Calculating A Pool Of Instrument Events
You can perform a number of calculations at init-time which lead to a list of instrument events. In this way you are producing a score, but inside an instrument. The score events are then executed later.
Using this opportunity we can introduce the scoreline / scoreline_i opcode. It is quite similar to the event / event_i opcode but has two major benefits:
- You can write more than one scoreline by using "{{" at the beginning and "}}" at the end.
- You can send a string to the subinstrument (which is not possible with the event opcode).
Let's look at a simple example for executing score events from an instrument using the scoreline opcode:
EXAMPLE 03F08_Generate_event_pool.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0; random seed different each time
instr 1 ;master instrument with event pool
scoreline_i {{i 2 0 2 7.09
i 2 2 2 8.04
i 2 4 2 8.03
i 2 6 1 8.04}}
endin
instr 2 ;plays the notes
asig pluck .2, cpspch(p4), cpspch(p4), 0, 1
aenv transeg 1, p3, 0, 0
outs asig*aenv, asig*aenv
endin
</CsInstruments>
<CsScore>
i 1 0 7
e
</CsScore>
</CsoundSynthesizer>
With good right, you might say: "OK, that's nice, but I can also write scorelines in the score itself!" That's right, but the advantage with the scoreline_i method is that you can render the score events in an instrument, and then send them out to one or more instruments to execute them. This can be done with the sprintf opcode, which produces the string for scoreline in an i-time loop (see the chapter about control structures).
EXAMPLE 03F09_Events_sprintf.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giPch ftgen 0, 0, 4, -2, 7.09, 8.04, 8.03, 8.04
seed 0; random seed different each time
instr 1 ; master instrument with event pool
itimes = 7 ;number of events to produce
icnt = 0 ;counter
istart = 0
Slines = ""
loop: ;start of the i-time loop
idur random 1, 2.9999 ;duration of each note:
idur = int(idur) ;either 1 or 2
itabndx random 0, 3.9999 ;index for the giPch table:
itabndx = int(itabndx) ;0-3
ipch table itabndx, giPch ;random pitch value from the table
Sline sprintf "i 2 %d %d %.2f\n", istart, idur, ipch ;new scoreline
Slines strcat Slines, Sline ;append to previous scorelines
istart = istart + idur ;recalculate start for next scoreline
loop_lt icnt, 1, itimes, loop ;end of the i-time loop
puts Slines, 1 ;print the scorelines
scoreline_i Slines ;execute them
iend = istart + idur ;calculate the total duration
p3 = iend ;set p3 to the sum of all durations
print p3 ;print it
endin
instr 2 ;plays the notes
asig pluck .2, cpspch(p4), cpspch(p4), 0, 1
aenv transeg 1, p3, 0, 0
outs asig*aenv, asig*aenv
endin
</CsInstruments>
<CsScore>
i 1 0 1 ;p3 is automatically set to the total duration
e
</CsScore>
</CsoundSynthesizer>
In this example, seven events have been rendered in an i-time loop in instrument 1. The result is stored in the string variable Slines. This string is given at i-time to scoreline_i, which executes them then one by one according to their starting times (p2), durations (p3) and other parameters.
Instead of collecting all score lines in a single string, you can also execute them inside the i-time loop. Also in this way all the single score lines are added to Csound's event pool. The next example shows an alternative version of the previous one by adding the instrument events one by one in the i-time loop, either with event_i (instr 1) or with scoreline_i (instr 2):
EXAMPLE 03F10_Events_collected.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giPch ftgen 0, 0, 4, -2, 7.09, 8.04, 8.03, 8.04
seed 0; random seed different each time
instr 1; master instrument with event_i
itimes = 7; number of events to produce
icnt = 0; counter
istart = 0
loop: ;start of the i-time loop
idur random 1, 2.9999; duration of each note:
idur = int(idur); either 1 or 2
itabndx random 0, 3.9999; index for the giPch table:
itabndx = int(itabndx); 0-3
ipch table itabndx, giPch; random pitch value from the table
event_i "i", 3, istart, idur, ipch; new instrument event
istart = istart + idur; recalculate start for next scoreline
loop_lt icnt, 1, itimes, loop; end of the i-time loop
iend = istart + idur; calculate the total duration
p3 = iend; set p3 to the sum of all durations
print p3; print it
endin
instr 2; master instrument with scoreline_i
itimes = 7; number of events to produce
icnt = 0; counter
istart = 0
loop: ;start of the i-time loop
idur random 1, 2.9999; duration of each note:
idur = int(idur); either 1 or 2
itabndx random 0, 3.9999; index for the giPch table:
itabndx = int(itabndx); 0-3
ipch table itabndx, giPch; random pitch value from the table
Sline sprintf "i 3 %d %d %.2f", istart, idur, ipch; new scoreline
scoreline_i Sline; execute it
puts Sline, 1; print it
istart = istart + idur; recalculate start for next scoreline
loop_lt icnt, 1, itimes, loop; end of the i-time loop
iend = istart + idur; calculate the total duration
p3 = iend; set p3 to the sum of all durations
print p3; print it
endin
instr 3; plays the notes
asig pluck .2, cpspch(p4), cpspch(p4), 0, 1
aenv transeg 1, p3, 0, 0
outs asig*aenv, asig*aenv
endin
</CsInstruments>
<CsScore>
i 1 0 1
i 2 14 1
e
</CsScore>
</CsoundSynthesizer>
Using Time Loops
As discussed above in the chapter about control structures, a time loop can be built in Csound either with the timout opcode or with the metro opcode. There were also simple examples for triggering instrument events using both methods. Here, a more complex example is given: A master instrument performs a time loop (choose either instr 1 for the timout method or instr 2 for the metro method) and triggers once in a loop a subinstrument. The subinstrument itself (instr 10) performs an i-time loop and triggers several instances of a sub-subinstrument (instr 100). Each instance performs a partial with an independent envelope for a bell-like additive synthesis.
EXAMPLE 03F11_Events_time_loop.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0
instr 1; time loop with timout. events are triggered by event_i (i-rate)
loop:
idurloop random 1, 4; duration of each loop
timout 0, idurloop, play
reinit loop
play:
idurins random 1, 5; duration of the triggered instrument
event_i "i", 10, 0, idurins; triggers instrument 10
endin
instr 2; time loop with metro. events are triggered by event (k-rate)
kfreq init 1; give a start value for the trigger frequency
kTrig metro kfreq
if kTrig == 1 then ;if trigger impulse:
kdur random 1, 5; random duration for instr 10
event "i", 10, 0, kdur; call instr 10
kfreq random .25, 1; set new value for trigger frequency
endif
endin
instr 10; triggers 8-13 partials
inumparts random 8, 14
inumparts = int(inumparts); 8-13 as integer
ibasoct random 5, 10; base pitch in octave values
ibasfreq = cpsoct(ibasoct)
ipan random .2, .8; random panning between left (0) and right (1)
icnt = 0; counter
loop:
event_i "i", 100, 0, p3, ibasfreq, icnt+1, inumparts, ipan
loop_lt icnt, 1, inumparts, loop
endin
instr 100; plays one partial
ibasfreq = p4; base frequency of sound mixture
ipartnum = p5; which partial is this (1 - N)
inumparts = p6; total number of partials
ipan = p7; panning
ifreqgen = ibasfreq * ipartnum; general frequency of this partial
ifreqdev random -10, 10; frequency deviation between -10% and +10%
; -- real frequency regarding deviation
ifreq = ifreqgen + (ifreqdev*ifreqgen)/100
ixtratim random 0, p3; calculate additional time for this partial
p3 = p3 + ixtratim; new duration of this partial
imaxamp = 1/inumparts; maximum amplitude
idbdev random -6, 0; random deviation in dB for this partial
iamp = imaxamp * ampdb(idbdev-ipartnum); higher partials are softer
ipandev random -.1, .1; panning deviation
ipan = ipan + ipandev
aEnv transeg 0, .005, 0, iamp, p3-.005, -10, 0
aSine poscil aEnv, ifreq
aL, aR pan2 aSine, ipan
outs aL, aR
prints "ibasfreq = %d, ipartial = %d, ifreq = %d%n",\
ibasfreq, ipartnum, ifreq
endin
</CsInstruments>
<CsScore>
i 1 0 300 ;try this, or the next line (or both)
;i 2 0 300
</CsScore>
</CsoundSynthesizer>
Which Opcode Should I Use?
Csound users are often confused about the variety of opcodes available to trigger instrument events. Should I use event, scoreline, schedule or schedkwhen? Should I use event or event_i?
Let us start with the latter, which actually leads to the general question about "i-rate" and "k-rate" opcodes.3 In short: Using event_i (the i-rate version) will only trigger an event once, when the instrument in which this opcode works is initiated. Using event (the k-rate version) will trigger an event potentially again and again, as long as the instrument runs, in each control cycle. This is a very simple example:
EXAMPLE 03F12_event_i_vs_event.csd
<CsoundSynthesizer> <CsOptions> -nm0 </CsOptions> <CsInstruments> sr=44100 ksmps = 32 ;set counters for the instances of Called_i and Called_k giInstCi init 1 giInstCk init 1 instr Call_i ;call another instrument at i-rate event_i "i", "Called_i", 0, 1 endin instr Call_k ;call another instrument at k-rate event "i", "Called_k", 0, 1 endin instr Called_i ;report that instrument starts and which instance prints "Instance #%d of Called_i is starting!\n", giInstCi ;increment number of instance for next instance giInstCi += 1 endin instr Called_k ;report that instrument starts and which instance prints " Instance #%d of Called_k is starting!\n", giInstCk ;increment number of instance for next instance giInstCk += 1 endin </CsInstruments> <CsScore> ;run "Call_i" for one second i "Call_i" 0 1 ;run "Call_k" for 1/100 seconds i "Call_k" 0 0.01 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
Although instrument "Call_i" runs for one second, the call to instrument "Called_i" is only performed once, because it is done with event_i: at initialization only. But instrument "Call_k" calls one instance of "Called_k" in each control cycle; so for the duration of 0.01 seconds of running instrument "Call_k", fourteen instances of instrument "Called_k" are being started.4 So this is the output:
Instance #1 of Called_i is starting!
Instance #1 of Called_k is starting!
Instance #2 of Called_k is starting!
Instance #3 of Called_k is starting!
Instance #4 of Called_k is starting!
Instance #5 of Called_k is starting!
Instance #6 of Called_k is starting!
Instance #7 of Called_k is starting!
Instance #8 of Called_k is starting!
Instance #9 of Called_k is starting!
Instance #10 of Called_k is starting!
Instance #11 of Called_k is starting!
Instance #12 of Called_k is starting!
Instance #13 of Called_k is starting!
Instance #14 of Called_k is starting!
So the first (and probably most important) decision in asking "which opcode should I use", is the answer to the question: "Do I need an i-rate or a k-rate opcode?"
i-rate Versions: schedule, event_i, scoreline_i
If you need an i-rate opcode to trigger an instrument event, schedule is the most basic choice. You use it actually exactly the same as writing any score event; just separting the parameter fields by commas rather by spaces:
schedule iInstrNum (or "InstrName"), iStart, iDur [, ip4] [, ip5] [...]
event_i is very similar:
event_i "i", iInstrNum (or "InstrName"), iStart, iDur [, ip4] [, ip5] [...]
The only difference between schedule and event_i is this: schedule can only trigger instruments, whereas event_i can also trigger "f" events (= build function tables).
Both, schedule and event_i have a restriction: they are not able to send strings in the parameter fields p4, p5, ... So, if you execute this code ...
schedule "bla", 0, 1, "blu"
... you will get this error message in the console:
ERROR: Unable to find opcode entry for 'schedule' with matching argument types:
Found: (null) schedule SccS
scoreline_i is designed to make this possible. It takes one or more lines of score statements which follow the same conventions as if written in the score section itself.5 If you enclose the line(s) by {{ and }}, you can include as many strings in it as you wish:
scoreline_i {{
i "bla" 0 1 "blu" "sound"
i "bla" 1 1 "brown" "earth"
}}
k-rate versions: event, scoreline, schedkwhen
If you need a k-rate opcode to trigger an instrument event, event is the basic choice. Its syntax is very similar to event_i, but as described above, it works at k-rate and you can also change all its arguments at k-rate:
event "i", kInstrNum (or "InstrName"), kStart, kDur [, kp4] [, kp5] [...]
Usually, you will not want to trigger another instrument each control cycle, but based on certain conditions. A very common case is a "ticking" periodic signal, whichs ticks are being used as trigger impulses. The typical code snippel using a metro and the event opcode would be:
kTrigger metro 1 ;"ticks" once a second if kTrigger == 1 then ;if it ticks event "i", "my_instr", 0, 1 ;call the instrument endif
In other words: This code would only use one control-cycle per second to call my_instr, and would do nothing in the other control cycles. The schedkwhen opcode simplifies such typical use cases, and adds some other useful arguments. This is the syntax:
schedkwhen kTrigger, kMinTim, kMaxNum, kInsrNum (or "InstrName"), kStart, kDur [, kp4] [, kp5] [...]
The kMinTim parameter specifies the time which has to be spent between two subsequent calls of the subinstrument. This is often quite useful as you may want to state: "Do not call the next instance of the subinstrument unless 0.1 seconds have been passed." If you set this parameter to zero, there will be no time limit for calling the subinstrument.
The kMaxNum parameter specifies the maximum number of instances which run simultaneously. Say, kMaxNum = 2 and there are indeed two instances of the subinstrument running, no other instance will be initiated. if you set this parameter to zero, there will be no limit for calling new instances.
So, with schedkwhen, we can write the above code snippet in two lines instead of four:
kTrigger metro 1 ;"ticks" once a second schedkwhen kTrigger, 0, 0, "my_instr", 0, 1
Only, you cannot pass strings as p-fields via schedkwhen (and event). So, very much similar as described above for i-rate opcodes, scoreline fills this gap. Usually we will use it with a condition, as we did for the event opcode:
kTrigger metro 1 ;"ticks" once a second
if kTrigger == 1 then
;if it ticks, call two instruments and pass strings as p-fields
scoreline {{
i "bla" 0 1 "blu" "sound"
i "bla" 1 1 "brown" "earth"
}}
endif
Recompilation
As it has been mentioned at the start of this chapter, since Csound6 you can re-compile any code in an already running Csound instance. Let us first see some simple examples for the general use, and then a more practical approach in CsoundQt.
compileorc / compilestr
The opcode compileorc refers to a definition of instruments which has been saved as an .orc ("orchestra") file. To see how it works, save this text in a simple text (ASCII) format as "to_recompile.orc":
instr 1 iAmp = .2 iFreq = 465 aSig oscils iAmp, iFreq, 0 outs aSig, aSig endin
Then save this csd in the same directory:
EXAMPLE 03F13_compileorc.csd
<CsoundSynthesizer> <CsOptions> -o dac -d -L stdin -Ma </CsOptions> <CsInstruments> sr = 44100 nchnls = 2 ksmps = 32 0dbfs = 1 massign 0, 9999 instr 9999 ires compileorc "to_recompile.orc" print ires ; 0 if compiled successfully event_i "i", 1, 0, 3 ;send event endin </CsInstruments> <CsScore> i 9999 0 1 </CsScore> </CsoundSynthesizer>
If you run this csd in the terminal, you should hear a three seconds beep, and the output should be like this:
SECTION 1:
new alloc for instr 9999:
instr 9999: ires = 0.000
new alloc for instr 1:
B 0.000 .. 1.000 T 1.000 TT 1.000 M: 0.20000 0.20000
B 1.000 .. 3.000 T 3.000 TT 3.000 M: 0.20000 0.20000
Score finished in csoundPerform().
inactive allocs returned to freespace
end of score. overall amps: 0.20000 0.20000
overall samples out of range: 0 0
0 errors in performance
Having understood this, it is easy to do the next step. Remove (or comment out) the score line "i 9999 0 1" so that the score is empty. If you start the csd now, Csound will run indefinitely. Now call instr 9999 by typing "i 9999 0 1" in the terminal window (if the option -L stdin works for your setup), or by pressing any MIDI key (if you have connected a keyboard). You should hear the same beep as before. But as the recompile.csd keeps running, you can change now the to_recompile.orc instrument. Try, for instance, another value for kFreq. Whenever this is done (do not forget to save the file) and you call again instr 9999 in recompile.csd, the new version of this instrument is compiled and then called immediately.
The other possibility to recompile code by using an opcode is compilestr. It will compile any instrument definition which is contained in a string. As this will be a string with several lines, you will usually use the '{{' delimiter for the start and '}}' for the end of the string. This is a basic example:
EXAMPLE 03F14_compilestr.csd
<CsoundSynthesizer>
<CsOptions>
-o dac -d
</CsOptions>
<CsInstruments>
sr = 44100
nchnls = 1
ksmps = 32
0dbfs = 1
instr 1
;will fail because of wrong code
ires compilestr {{
instr 2
a1 oscilb p4, p5, 0
out a1
endin
}}
print ires ; returns -1 because not successfull
;will compile ...
ires compilestr {{
instr 2
a1 oscils p4, p5, 0
out a1
endin
}}
print ires ; ... and returns 0
;call the new instrument
;(note that the overall performance is extended)
scoreline_i "i 2 0 3 .2 415"
endin
</CsInstruments>
<CsScore>
i1 0 1
</CsScore>
</CsoundSynthesizer>
As you see, instrument 2 is defined inside instrument 1, and compiled via compilestr. in case you can change this string in real-time (for instance in receiving it via OSC), you can add any new definition of instruments on the fly. But much more elegant is to use the related method of the Csound API, as CsoundQt does.
Re-Compilation in CsoundQt
(The following description is only valid if you have CsoundQt with PythonQt support. If so, your CsoundQt application should be called CsoundQt-d-py-cs6 or similar. If the "-py" is missing, you will probably not have PythonQt support.)
To see how easy it is to re-compile code of a running Csound instance, load this csd in CsoundQt:
EXAMPLE 03F15_Recompile_in_CsoundQt.csd
<CsoundSynthesizer> <CsInstruments> sr = 44100 nchnls = 1 ksmps = 32 0dbfs = 1 instr 1 a1 poscil .2, 500 out a1 endin </CsInstruments> <CsScore> r 1000 i 1 0 1 </CsScore> </CsoundSynthesizer>
The r-statement repeats the call to instr 1 for 1000 times. Now change the frequency of 500 in instr 1 to say 800. You will hear no change, because this has not been compiled yet. But when you now select the instrument definition (including the instr ... endin) and then choose Edit -> Evaluate selection, you will hear that in the next call of instrument 1 the frequency has changed. (Instead of selecting code and evaluation the selection, you can also place the cursor inside an instrument and then choose Edit -> Evaluate section.)
You can also insert new instrument definitions, and then call it with CsoundQt's Live event sheet. You even need not save it - instead you can save several results of your live coding without stopping Csound. Have fun ...
Links And Related Opcodes
Links
A great collection of interactive examples with FLTK widgets by Iain McCurdy can be found here. See particularily the "Realtime Score Generation" section. Recently, the collection has been ported to QuteCsound by René Jopi, and is part of QuteCsound's example menu.
An extended example for calculating score events at i-time can be found in the Re-Generation of Stockhausen's "Studie II" by Joachim Heintz (also included in the QuteCsound Examples menu).
Related Opcodes
event_i / event: Generate an instrument event at i-time (event_i) or at k-time (event). Easy to use, but you cannot send a string to the subinstrument.
scoreline_i / scoreline: Generate an instrument at i-time (scoreline_i) or at k-time (scoreline). Like event_i/event, but you can send to more than one instrument but unlike event_i/event you can send strings. On the other hand, you must usually preformat your scoreline-string using sprintf.
sprintf / sprintfk: Generate a formatted string at i-time (sprintf) or k-time (sprintfk), and store it as a string-variable.
-+max_str_len=10000: Option in the "CsOptions" tag of a .csd file which extend the maximum string length to 9999 characters.
massign: Assigns the incoming MIDI events to a particular instrument. It is also possible to prevent any assigment by this opcode.
cpsmidi / ampmidi: Returns the frequency / velocity of a pressed MIDI key.
release: Returns "1" if the last k-cycle of an instrument has begun.
xtratim: Adds an additional time to the duration (p3) of an instrument.
turnoff / turnoff2: Turns an instrument off; either by the instrument itself (turnoff), or from another instrument and with several options (turnoff2).
-p3 / -p1: A negative duration (p3) turns an instrument on "indefinitely"; a negative instrument number (p1) turns this instrument off. See the examples at the beginning of this chapter.
-L stdin: Option in the "CsOptions" tag of a .csd file which lets you type in realtime score events.
timout: Allows you to perform time loops at i-time with reinitalization passes.
metro: Outputs momentary 1s with a definable (and variable) frequency. Can be used to perform a time loop at k-rate.
follow: Envelope follower.
- This has been described incorrectly in the first two issues of this manual.^
- There are also some video tutorials: http://www.youtube.com/watch?v=O9WU7DzdUmE http://www.youtube.com/watch?v=Hs3eO7o349k http://www.youtube.com/watch?v=yUMzp6556Kw^
- See chapter 03A about Initialization and Performance Pass for a detailed discussion.^
- As for a sample rate of 44100 Hz (sr=44100) and a control period od 32 samples (ksmps=32), we have 1378 control periods in one second. So 0.01 seconds will perform 14 control cycles.^
- This means that score parameter fields are separated by spaces, not by commas.^
Csound: Userdefinedopcodes
USER DEFINED OPCODES
Opcodes are the core units of everything that Csound does. They are like little machines that do a job, and programming is akin to connecting these little machines to perform a larger job. An opcode usually has something which goes into it: the inputs or arguments, and usually it has something which comes out of it: the output which is stored in one or more variables. Opcodes are written in the programming language C (that is where the name "Csound" comes from). If you want to create a new opcode in Csound, you must write it in C. How to do this is described in the Extending Csound chapter of this manual, and is also described in the relevant chapter of the Canonical Csound Reference Manual.
There is, however, a way of writing your own opcodes in the Csound Language itself. The opcodes which are written in this way, are called User Defined Opcodes or "UDO"s. A UDO behaves in the same way as a standard opcode: it has input arguments, and usually one or more output variables. They run at i-time or at k-time. You use them as part of the Csound Language after you have defined and loaded them.
User Defined Opcodes have many valuable properties. They make your instrument code clearer because they allow you to create abstractions of blocks of code. Once a UDO has been defined it can be recalled and repeated many times within an orchestra, each repetition requiring only a single line of code. UDOs allow you to build up your own library of functions you need and return to frequently in your work. In this way, you build your own Csound dialect within the Csound Language. UDOs also represent a convenient format with which to share your work in Csound with other users.
This chapter explains, initially with a very basic example, how you can build your own UDOs, and what options they offer. Following this, the practice of loading UDOs in your .csd file is shown, followed by some tips in regard to some unique capabilities of UDOs. Before the "Links And Related Opcodes" section at the end, some examples are shown for different User Defined Opcode definitions and applications.
If you want to write a User Defined Opcode in Csound6 which uses arrays, have a look at the end of chapter 03E to see their usage and naming conventions.
Transforming Csound Instrument Code To A User Defined Opcode
Writing a User Defined Opcode is actually very easy and straightforward. It mainly means to extract a portion of usual Csound instrument code, and put it in the frame of a UDO. Let's start with the instrument code:
EXAMPLE 03G01_Pre_UDO.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
seed 0
instr 1
aDel init 0; initialize delay signal
iFb = .7; feedback multiplier
aSnd rand .2; white noise
kdB randomi -18, -6, .4; random movement between -18 and -6
aSnd = aSnd * ampdb(kdB); applied as dB to noise
kFiltFq randomi 100, 1000, 1; random movement between 100 and 1000
aFilt reson aSnd, kFiltFq, kFiltFq/5; applied as filter center frequency
aFilt balance aFilt, aSnd; bring aFilt to the volume of aSnd
aDelTm randomi .1, .8, .2; random movement between .1 and .8 as delay time
aDel vdelayx aFilt + iFb*aDel, aDelTm, 1, 128; variable delay
kdbFilt randomi -12, 0, 1; two random movements between -12 and 0 (dB) ...
kdbDel randomi -12, 0, 1; ... for the filtered and the delayed signal
aOut = aFilt*ampdb(kdbFilt) + aDel*ampdb(kdbDel); mix it
outs aOut, aOut
endin
</CsInstruments>
<CsScore>
i 1 0 60
</CsScore>
</CsoundSynthesizer>
This is a filtered noise, and its delay, which is fed back again into the delay line at a certain ratio iFb. The filter is moving as kFiltFq randomly between 100 and 1000 Hz. The volume of the filtered noise is moving as kdB randomly between -18 dB and -6 dB. The delay time moves between 0.1 and 0.8 seconds, and then both signals are mixed together.
Basic Example
If this signal processing unit is to be transformed into a User Defined Opcode, the first question is about the extend of the code that will be encapsulated: where the UDO code will begin and end? The first solution could be a radical, and possibly bad, approach: to transform the whole instrument into a UDO.
EXAMPLE 03G02_All_to_UDO.csd
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
seed 0
opcode FiltFb, 0, 0
aDel init 0; initialize delay signal
iFb = .7; feedback multiplier
aSnd rand .2; white noise
kdB randomi -18, -6, .4; random movement between -18 and -6
aSnd = aSnd * ampdb(kdB); applied as dB to noise
kFiltFq randomi 100, 1000, 1; random movement between 100 and 1000
aFilt reson aSnd, kFiltFq, kFiltFq/5; applied as filter center frequency
aFilt balance aFilt, aSnd; bring aFilt to the volume of aSnd
aDelTm randomi .1, .8, .2; random movement between .1 and .8 as delay time
aDel vdelayx aFilt + iFb*aDel, aDelTm, 1, 128; variable delay
kdbFilt randomi -12, 0, 1; two random movements between -12 and 0 (dB) ...
kdbDel randomi -12, 0, 1; ... for the filtered and the delayed signal
aOut = aFilt*ampdb(kdbFilt) + aDel*ampdb(kdbDel); mix it
outs aOut, aOut
endop
instr 1
FiltFb
endin
</CsInstruments>
<CsScore>
i 1 0 60
</CsScore>
</CsoundSynthesizer>
Before we continue the discussion about the quality of this transformation, we should have a look at the syntax first. The general syntax for a User Defined Opcode is:
opcode name, outtypes, intypes ... endop
Here, the name of the UDO is FiltFb. You are free to use any name, but it is suggested that you begin the name with a capital letter. By doing this, you avoid duplicating the name of most of the pre-existing opcodes1 which normally start with a lower case letter. As we have no input arguments and no output arguments for this first version of FiltFb, both outtypes and intypes are set to zero. Similar to the instr ... endin block of a normal instrument definition, for a UDO the opcode ... endop keywords begin and end the UDO definition block. In the instrument, the UDO is called like a normal opcode by using its name, and in the same line the input arguments are listed on the right and the output arguments on the left. In the previous a example, 'FiltFb' has no input and output arguments so it is called by just using its name:
instr 1
FiltFb
endin
Now - why is this UDO more or less useless? It achieves nothing, when compared to the original non UDO version, and in fact looses some of the advantages of the instrument defined version. Firstly, it is not advisable to include this line in the UDO:
outs aOut, aOut
This statement writes the audio signal aOut from inside the UDO to the output device. Imagine you want to change the output channels, or you want to add any signal modifier after the opcode. This would be impossible with this statement. So instead of including the 'outs' opcode, we give the FiltFb UDO an audio output:
xout aOut
The xout statement of a UDO definition works like the "outlets" in PD or Max, sending the result(s) of an opcode back to the caller instrument.
Now let us consider the UDO's input arguments, choose which processes should be carried out within the FiltFb unit, and what aspects would offer greater flexibility if controllable from outside the UDO. First, the aSnd parameter should not be restricted to a white noise with amplitude 0.2, but should be an input (like a "signal inlet" in PD/Max). This is implemented using the line:
aSnd xin
Both the output and the input type must be declared in the first line of the UDO definition, whether they are i-, k- or a-variables. So instead of "opcode FiltFb, 0, 0" the statement has changed now to "opcode FiltFb, a, a", because we have both input and output as a-variable.
The UDO is now much more flexible and logical: it takes any audio input, it performs the filtered delay and feedback processing, and returns the result as another audio signal. In the next example, instrument 1 does exactly the same as before. Instrument 2 has live input instead.
EXAMPLE 03G03_UDO_more_flex.csd
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
seed 0
opcode FiltFb, a, a
aSnd xin
aDel init 0; initialize delay signal
iFb = .7; feedback multiplier
kdB randomi -18, -6, .4; random movement between -18 and -6
aSnd = aSnd * ampdb(kdB); applied as dB to noise
kFiltFq randomi 100, 1000, 1; random movement between 100 and 1000
aFilt reson aSnd, kFiltFq, kFiltFq/5; applied as filter center frequency
aFilt balance aFilt, aSnd; bring aFilt to the volume of aSnd
aDelTm randomi .1, .8, .2; random movement between .1 and .8 as delay time
aDel vdelayx aFilt + iFb*aDel, aDelTm, 1, 128; variable delay
kdbFilt randomi -12, 0, 1; two random movements between -12 and 0 (dB) ...
kdbDel randomi -12, 0, 1; ... for the filtered and the delayed signal
aOut = aFilt*ampdb(kdbFilt) + aDel*ampdb(kdbDel); mix it
xout aOut
endop
instr 1; white noise input
aSnd rand .2
aOut FiltFb aSnd
outs aOut, aOut
endin
instr 2; live audio input
aSnd inch 1; input from channel 1
aOut FiltFb aSnd
outs aOut, aOut
endin
</CsInstruments>
<CsScore>
i 1 0 60 ;change to i 2 for live audio input
</CsScore>
</CsoundSynthesizer>
Is There an Optimal Design for a User Defined Opcode?
Is this now the optimal version of the FiltFb User Defined Opcode? Obviously there are other parts of the opcode definiton which could be controllable from outside: the feedback multiplier iFb, the random movement of the input signal kdB, the random movement of the filter frequency kFiltFq, and the random movements of the output mix kdbSnd and kdbDel. Is it better to put them outside of the opcode definition, or is it better to leave them inside?
There is no general answer. It depends on the degree of abstraction you desire or you prefer to relinquish. If you are working on a piece for which all of the parameters settings are already defined as required in the UDO, then control from the caller instrument may not be necessary . The advantage of minimizing the number of input and output arguments is the simplification in using the UDO. The more flexibility you require from your UDO however, the greater the number of input arguments that will be required. Providing more control is better for a later reusability, but may be unnecessarily complicated.
Perhaps it is the best solution to have one abstract definition which performs one task, and to create a derivative - also as UDO - fine tuned for the particular project you are working on. The final example demonstrates the definition of a general and more abstract UDO FiltFb, and its various applications: instrument 1 defines the specifications in the instrument itself; instrument 2 uses a second UDO Opus123_FiltFb for this purpose; instrument 3 sets the general FiltFb in a new context of two varying delay lines with a buzz sound as input signal.
EXAMPLE 03G04_UDO_calls_UDO.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
seed 0
opcode FiltFb, aa, akkkia
; -- DELAY AND FEEDBACK OF A BAND FILTERED INPUT SIGNAL --
;input: aSnd = input sound
; kFb = feedback multiplier (0-1)
; kFiltFq: center frequency for the reson band filter (Hz)
; kQ = band width of reson filter as kFiltFq/kQ
; iMaxDel = maximum delay time in seconds
; aDelTm = delay time
;output: aFilt = filtered and balanced aSnd
; aDel = delay and feedback of aFilt
aSnd, kFb, kFiltFq, kQ, iMaxDel, aDelTm xin
aDel init 0
aFilt reson aSnd, kFiltFq, kFiltFq/kQ
aFilt balance aFilt, aSnd
aDel vdelayx aFilt + kFb*aDel, aDelTm, iMaxDel, 128; variable delay
xout aFilt, aDel
endop
opcode Opus123_FiltFb, a, a
;;the udo FiltFb here in my opus 123 :)
;input = aSnd
;output = filtered and delayed aSnd in different mixtures
aSnd xin
kdB randomi -18, -6, .4; random movement between -18 and -6
aSnd = aSnd * ampdb(kdB); applied as dB to noise
kFiltFq randomi 100, 1000, 1; random movement between 100 and 1000
iQ = 5
iFb = .7; feedback multiplier
aDelTm randomi .1, .8, .2; random movement between .1 and .8 as delay time
aFilt, aDel FiltFb aSnd, iFb, kFiltFq, iQ, 1, aDelTm
kdbFilt randomi -12, 0, 1; two random movements between -12 and 0 (dB) ...
kdbDel randomi -12, 0, 1; ... for the noise and the delay signal
aOut = aFilt*ampdb(kdbFilt) + aDel*ampdb(kdbDel); mix it
xout aOut
endop
instr 1; well known context as instrument
aSnd rand .2
kdB randomi -18, -6, .4; random movement between -18 and -6
aSnd = aSnd * ampdb(kdB); applied as dB to noise
kFiltFq randomi 100, 1000, 1; random movement between 100 and 1000
iQ = 5
iFb = .7; feedback multiplier
aDelTm randomi .1, .8, .2; random movement between .1 and .8 as delay time
aFilt, aDel FiltFb aSnd, iFb, kFiltFq, iQ, 1, aDelTm
kdbFilt randomi -12, 0, 1; two random movements between -12 and 0 (dB) ...
kdbDel randomi -12, 0, 1; ... for the noise and the delay signal
aOut = aFilt*ampdb(kdbFilt) + aDel*ampdb(kdbDel); mix it
aOut linen aOut, .1, p3, 3
outs aOut, aOut
endin
instr 2; well known context UDO which embeds another UDO
aSnd rand .2
aOut Opus123_FiltFb aSnd
aOut linen aOut, .1, p3, 3
outs aOut, aOut
endin
instr 3; other context: two delay lines with buzz
kFreq randomh 200, 400, .08; frequency for buzzer
aSnd buzz .2, kFreq, 100, giSine; buzzer as aSnd
kFiltFq randomi 100, 1000, .2; center frequency
aDelTm1 randomi .1, .8, .2; time for first delay line
aDelTm2 randomi .1, .8, .2; time for second delay line
kFb1 randomi .8, 1, .1; feedback for first delay line
kFb2 randomi .8, 1, .1; feedback for second delay line
a0, aDel1 FiltFb aSnd, kFb1, kFiltFq, 1, 1, aDelTm1; delay signal 1
a0, aDel2 FiltFb aSnd, kFb2, kFiltFq, 1, 1, aDelTm2; delay signal 2
aDel1 linen aDel1, .1, p3, 3
aDel2 linen aDel2, .1, p3, 3
outs aDel1, aDel2
endin
</CsInstruments>
<CsScore>
i 1 0 30
i 2 31 30
i 3 62 120
</CsScore>
</CsoundSynthesizer>
The good thing about the different possibilities of writing a more specified UDO, or a more generalized: You needn't decide this at the beginning of your work. Just start with any formulation you find useful in a certain situation. If you continue and see that you should have some more parameters accessible, it should be easy to rewrite the UDO. Just be careful not to confuse the different versions you create. Use names like Faulty1, Faulty2 etc. instead of overwriting Faulty. Making use of extensive commenting when you initially create the UDO will make it easier to adapt the UDO at a later time. What are the inputs (including the measurement units they use such as Hertz or seconds)? What are the outputs? - How you do this, is up to you and depends on your style and your preference.
How to Use the User Defined Opcode Facility in Practice
In this section, we will address the main points of using UDOs: what you must bear in mind when loading them, what special features they offer, what restrictions you must be aware of and how you can build your own language with them.
Loading User Defined Opcodes in the Orchestra Header
As can be seen from the examples above, User Defined Opcodes must be defined in the orchestra header (which is sometimes called "instrument 0").
You can load as many User Defined Opcodes into a Csound orchestra as you wish. As long as they do not depend on each other, their order is arbitrarily. If UDO Opus123_FiltFb uses the UDO FiltFb for its definition (see the example above), you must first load FiltFb, and then Opus123_FiltFb. If not, you will get an error like this:
orch compiler: opcode Opus123_FiltFb a a error: no legal opcode, line 25: aFilt, aDel FiltFb aSnd, iFb, kFiltFq, iQ, 1, aDelTm
Loading By An #include File
Definitions of User Defined Opcodes can also be loaded into a .csd file by an "#include" statement. What you must do is the following:
- Save your opcode definitions in a plain text file, for instance "MyOpcodes.txt".
- If this file is in the same directory as your .csd file, you can just call it by the statement:
#include "MyOpcodes.txt"
- If "MyOpcodes.txt" is in a different directory, you must call it by the full path name, for instance:
#include "/Users/me/Documents/Csound/UDO/MyOpcodes.txt"
As always, make sure that the "#include" statement is the last one in the orchestra header, and that the logical order is accepted if one opcode depends on another.
If you work with User Defined Opcodes a lot, and build up a collection of them, the #include feature allows you easily import several or all of them to your .csd file.
The setksmps Feature
The ksmps assignment in the orchestra header cannot be changed during the performance of a .csd file. But in a User Defined Opcode you have the unique possibility of changing this value by a local assignment. If you use a setksmps statement in your UDO, you can have a locally smaller value for the number of samples per control cycle in the UDO. In the following example, the print statement in the UDO prints ten times compared to one time in the instrument, because ksmps in the UDO is 10 times smaller:
EXAMPLE 03G06_UDO_setksmps.csd
<CsoundSynthesizer> <CsInstruments> ;Example by Joachim Heintz sr = 44100 ksmps = 44100 ;very high because of printing opcode Faster, 0, 0 setksmps 4410 ;local ksmps is 1/10 of global ksmps printks "UDO print!%n", 0 endop instr 1 printks "Instr print!%n", 0 ;print each control period (once per second) Faster ;print 10 times per second because of local ksmps endin </CsInstruments> <CsScore> i 1 0 2 </CsScore> </CsoundSynthesizer>
Default Arguments
For i-time arguments, you can use a simple feature to set default values:
- "o" (instead of "i") defaults to 0
- "p" (instead of "i") defaults to 1
- "j" (instead of "i") defaults to -1
For k-time arguments, you can use since Csound 5.18 these default values:
- "O" (instead of "k") defaults to 0
- "P" (instead of "k") defaults to 1
- "V" (instead of "k") defaults to 0.5
So you can omit these arguments - in this case the default values will be used. If you give an input argument instead, the default value will be overwritten:
EXAMPLE 03G07_UDO_default_args.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Joachim Heintz
opcode Defaults, iii, opj
ia, ib, ic xin
xout ia, ib, ic
endop
instr 1
ia, ib, ic Defaults
print ia, ib, ic
ia, ib, ic Defaults 10
print ia, ib, ic
ia, ib, ic Defaults 10, 100
print ia, ib, ic
ia, ib, ic Defaults 10, 100, 1000
print ia, ib, ic
endin
</CsInstruments>
<CsScore>
i 1 0 0
</CsScore>
</CsoundSynthesizer>
Recursive User Defined Opcodes
Recursion means that a function can call itself. This is a feature which can be useful in many situations. Also User Defined Opcodes can be recursive. You can do many things with a recursive UDO which you cannot do in any other way; at least not in a simliarly simple way. This is an example of generating eight partials by a recursive UDO. See the last example in the next section for a more musical application of a recursive UDO.
EXAMPLE 03G08_Recursive_UDO.csd
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
opcode Recursion, a, iip
;input: frequency, number of partials, first partial (default=1)
ifreq, inparts, istart xin
iamp = 1/inparts/istart ;decreasing amplitudes for higher partials
if istart < inparts then ;if inparts have not yet reached
acall Recursion ifreq, inparts, istart+1 ;call another instance of this UDO
endif
aout oscils iamp, ifreq*istart, 0 ;execute this partial
aout = aout + acall ;add the audio signals
xout aout
endop
instr 1
amix Recursion 400, 8 ;8 partials with a base frequency of 400 Hz
aout linen amix, .01, p3, .1
outs aout, aout
endin
</CsInstruments>
<CsScore>
i 1 0 1
</CsScore>
</CsoundSynthesizer>
Examples
We will focus here on some examples which will hopefully show the wide range of User Defined Opcodes. Some of them are adaptions of examples from previous chapters about the Csound Syntax. Much more examples can be found in the User-Defined Opcode Database, editied by Steven Yi.
Play A Mono Or Stereo Soundfile
Csound is often very strict and gives errors where other applications might 'turn a blind eye'. This is also the case if you read a soundfile using one of Csound's opcodes: soundin, diskin or diskin2. If your soundfile is mono, you must use the mono version, which has one audio signal as output. If your soundfile is stereo, you must use the stereo version, which outputs two audio signals. If you want a stereo output, but you happen to have a mono soundfile as input, you will get the error message:
INIT ERROR in ...: number of output args inconsistent with number of file channels
It may be more useful to have an opcode which works for both, mono and stereo files as input. This is a ideal job for a UDO. Two versions are possible: FilePlay1 returns always one audio signal (if the file is stereo it uses just the first channel), FilePlay2 returns always two audio signals (if the file is mono it duplicates this to both channels). We can use the default arguments to make this opcode behave exactly as diskin2:
EXAMPLE 03G09_UDO_FilePlay.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
opcode FilePlay1, a, Skoooooo
;gives mono output regardless your soundfile is mono or stereo
;(if stereo, just the first channel is used)
;see diskin2 page of the csound manual for information about the input arguments
Sfil, kspeed, iskip, iloop, iformat, iwsize, ibufsize, iskipinit xin
ichn filenchnls Sfil
if ichn == 1 then
aout diskin2 Sfil, kspeed, iskip, iloop, iformat, iwsize,\
ibufsize, iskipinit
else
aout, a0 diskin2 Sfil, kspeed, iskip, iloop, iformat, iwsize,\
ibufsize, iskipinit
endif
xout aout
endop
opcode FilePlay2, aa, Skoooooo
;gives stereo output regardless your soundfile is mono or stereo
;see diskin2 page of the csound manual for information about the input arguments
Sfil, kspeed, iskip, iloop, iformat, iwsize, ibufsize, iskipinit xin
ichn filenchnls Sfil
if ichn == 1 then
aL diskin2 Sfil, kspeed, iskip, iloop, iformat, iwsize,\
ibufsize, iskipinit
aR = aL
else
aL, aR diskin2 Sfil, kspeed, iskip, iloop, iformat, iwsize,\
ibufsize, iskipinit
endif
xout aL, aR
endop
instr 1
aMono FilePlay1 "fox.wav", 1
outs aMono, aMono
endin
instr 2
aL, aR FilePlay2 "fox.wav", 1
outs aL, aR
endin
</CsInstruments>
<CsScore>
i 1 0 4
i 2 4 4
</CsScore>
</CsoundSynthesizer>
Change the Content of a Function Table
In example 03C11_Table_random_dev.csd, a function table has been changed at performance time, once a second, by random deviations. This can be easily transformed to a User Defined Opcode. It takes the function table variable, a trigger signal, and the random deviation in percent as input. In each control cycle where the trigger signal is "1", the table values are read. The random deviation is applied, and the changed values are written again into the table. Here, the tab/tabw opcodes are used to make sure that also non-power-of-two tables can be used.
EXAMPLE 03G10_UDO_rand_dev.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 441
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 256, 10, 1; sine wave
seed 0; each time different seed
opcode TabDirtk, 0, ikk
;"dirties" a function table by applying random deviations at a k-rate trigger
;input: function table, trigger (1 = perform manipulation),
;deviation as percentage
ift, ktrig, kperc xin
if ktrig == 1 then ;just work if you get a trigger signal
kndx = 0
loop:
krand random -kperc/100, kperc/100
kval tab kndx, ift; read old value
knewval = kval + (kval * krand); calculate new value
tabw knewval, kndx, giSine; write new value
loop_lt kndx, 1, ftlen(ift), loop; loop construction
endif
endop
instr 1
kTrig metro 1, .00001 ;trigger signal once per second
TabDirtk giSine, kTrig, 10
aSig poscil .2, 400, giSine
outs aSig, aSig
endin
</CsInstruments>
<CsScore>
i 1 0 10
</CsScore>
</CsoundSynthesizer>
Of course you can also change the content of a function table at init-time. The next example permutes a series of numbers randomly each time it is called. For this purpose, first the input function table iTabin is copied as iCopy. This is necessary because we do not want to change iTabin in any way. Next a random index in iCopy is created and the value at this location in iTabin is written at the beginning of iTabout, which contains the permuted results. At the end of this cycle, each value in iCopy which has a larger index than the one which has just been read, is shifted one position to the left. So now iCopy has become one position smaller - not in table size but in the number of values to read. This procedure is continued until all values from iCopy are reflected in iTabout:
EXAMPLE 03G11_TabPermRnd.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Joachim Heintz
giVals ftgen 0, 0, -12, -2, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
seed 0; each time different seed
opcode TabPermRand_i, i, i
;permuts randomly the values of the input table
;and creates an output table for the result
iTabin xin
itablen = ftlen(iTabin)
iTabout ftgen 0, 0, -itablen, 2, 0 ;create empty output table
iCopy ftgen 0, 0, -itablen, 2, 0 ;create empty copy of input table
tableicopy iCopy, iTabin ;write values of iTabin into iCopy
icplen init itablen ;number of values in iCopy
indxwt init 0 ;index of writing in iTabout
loop:
indxrd random 0, icplen - .0001; random read index in iCopy
indxrd = int(indxrd)
ival tab_i indxrd, iCopy; read the value
tabw_i ival, indxwt, iTabout; write it to iTabout
; -- shift values in iCopy larger than indxrd one position to the left
shift:
if indxrd < icplen-1 then ;if indxrd has not been the last table value
ivalshft tab_i indxrd+1, iCopy ;take the value to the right ...
tabw_i ivalshft, indxrd, iCopy ;...and write it to indxrd position
indxrd = indxrd + 1 ;then go to the next position
igoto shift ;return to shift and see if there is anything left to do
endif
indxwt = indxwt + 1 ;increase the index of writing in iTabout
loop_gt icplen, 1, 0, loop ;loop as long as there is ;
;a value in iCopy
ftfree iCopy, 0 ;delete the copy table
xout iTabout ;return the number of iTabout
endop
instr 1
iPerm TabPermRand_i giVals ;perform permutation
;print the result
indx = 0
Sres = "Result:"
print:
ival tab_i indx, iPerm
Sprint sprintf "%s %d", Sres, ival
Sres = Sprint
loop_lt indx, 1, 12, print
puts Sres, 1
endin
instr 2; the same but performed ten times
icnt = 0
loop:
iPerm TabPermRand_i giVals ;perform permutation
;print the result
indx = 0
Sres = "Result:"
print:
ival tab_i indx, iPerm
Sprint sprintf "%s %d", Sres, ival
Sres = Sprint
loop_lt indx, 1, 12, print
puts Sres, 1
loop_lt icnt, 1, 10, loop
endin
</CsInstruments>
<CsScore>
i 1 0 0
i 2 0 0
</CsScore>
</CsoundSynthesizer>
Print the Content of a Function Table
There is no opcode in Csound for printing the contents of a function table, but one can be created as a UDO.2 Again a loop is needed for checking the values and putting them into a string which can then be printed. In addition, some options can be given for the print precision and for the number of elements in a line.
EXAMPLE 03G12_TableDumpSimp.csd
<CsoundSynthesizer>
<CsOptions>
-ndm0 -+max_str_len=10000
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
gitab ftgen 1, 0, -7, -2, 0, 1, 2, 3, 4, 5, 6
gisin ftgen 2, 0, 128, 10, 1
opcode TableDumpSimp, 0, ijo
;prints the content of a table in a simple way
;input: function table, float precision while printing (default = 3),
;parameters per row (default = 10, maximum = 32)
ifn, iprec, ippr xin
iprec = (iprec == -1 ? 3 : iprec)
ippr = (ippr == 0 ? 10 : ippr)
iend = ftlen(ifn)
indx = 0
Sformat sprintf "%%.%df\t", iprec
Sdump = ""
loop:
ival tab_i indx, ifn
Snew sprintf Sformat, ival
Sdump strcat Sdump, Snew
indx = indx + 1
imod = indx % ippr
if imod == 0 then
puts Sdump, 1
Sdump = ""
endif
if indx < iend igoto loop
puts Sdump, 1
endop
instr 1
TableDumpSimp p4, p5, p6
prints "%n"
endin
</CsInstruments>
<CsScore>
;i1 st dur ftab prec ppr
i1 0 0 1 -1
i1 . . 1 0
i1 . . 2 3 10
i1 . . 2 6 32
</CsScore>
</CsoundSynthesizer>
A Recursive User Defined Opcode for Additive Synthesis
In the last example of the chapter about Triggering Instrument Events a number of partials were synthesized, each with a random frequency deviation of up to 10% compared to precise harmonic spectrum frequencies and a unique duration for each partial. This can also be written as a recursive UDO. Each UDO generates one partial, and calls the UDO again until the last partial is generated. Now the code can be reduced to two instruments: instrument 1 performs the time loop, calculates the basic values for one note, and triggers the event. Then instrument 11 is called which feeds the UDO with the values and passes the audio signals to the output.
EXAMPLE 03G13_UDO_Recursive_AddSynth.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
seed 0
opcode PlayPartials, aa, iiipo
;plays inumparts partials with frequency deviation and own envelopes and
;durations for each partial
;ibasfreq: base frequency of sound mixture
;inumparts: total number of partials
;ipan: panning
;ipartnum: which partial is this (1 - N, default=1)
;ixtratim: extra time in addition to p3 needed for this partial (default=0)
ibasfreq, inumparts, ipan, ipartnum, ixtratim xin
ifreqgen = ibasfreq * ipartnum; general frequency of this partial
ifreqdev random -10, 10; frequency deviation between -10% and +10%
ifreq = ifreqgen + (ifreqdev*ifreqgen)/100; real frequency
ixtratim1 random 0, p3; calculate additional time for this partial
imaxamp = 1/inumparts; maximum amplitude
idbdev random -6, 0; random deviation in dB for this partial
iamp = imaxamp * ampdb(idbdev-ipartnum); higher partials are softer
ipandev random -.1, .1; panning deviation
ipan = ipan + ipandev
aEnv transeg 0, .005, 0, iamp, p3+ixtratim1-.005, -10, 0; envelope
aSine poscil aEnv, ifreq, giSine
aL1, aR1 pan2 aSine, ipan
if ixtratim1 > ixtratim then
ixtratim = ixtratim1 ;set ixtratim to the ixtratim1 if the latter is larger
endif
if ipartnum < inumparts then ;if this is not the last partial
; -- call the next one
aL2, aR2 PlayPartials ibasfreq, inumparts, ipan, ipartnum+1, ixtratim
else ;if this is the last partial
p3 = p3 + ixtratim; reset p3 to the longest ixtratim value
endif
xout aL1+aL2, aR1+aR2
endop
instr 1; time loop with metro
kfreq init 1; give a start value for the trigger frequency
kTrig metro kfreq
if kTrig == 1 then ;if trigger impulse:
kdur random 1, 5; random duration for instr 10
knumparts random 8, 14
knumparts = int(knumparts); 8-13 partials
kbasoct random 5, 10; base pitch in octave values
kbasfreq = cpsoct(kbasoct) ;base frequency
kpan random .2, .8; random panning between left (0) and right (1)
event "i", 11, 0, kdur, kbasfreq, knumparts, kpan; call instr 11
kfreq random .25, 1; set new value for trigger frequency
endif
endin
instr 11; plays one mixture with 8-13 partials
aL, aR PlayPartials p4, p5, p6
outs aL, aR
endin
</CsInstruments>
<CsScore>
i 1 0 300
</CsScore>
</CsoundSynthesizer>
Using Strings as Arrays
For some situations it can be very useful to use strings in Csound as a collection of single strings or numbers. This is what programming languages call a list or an array. Csound does not provide opcodes for this purpose, but you can define these opcodes as UDOs. A set of these UDOs can then be used like this:
ilen StrayLen "a b c d e" ilen -> 5 Sel StrayGetEl "a b c d e", 0 Sel -> "a" inum StrayGetNum "1 2 3 4 5", 0 inum -> 1 ipos StrayElMem "a b c d e", "c" ipos -> 2 ipos StrayNumMem "1 2 3 4 5", 3 ipos -> 2 Sres StraySetEl "a b c d e", "go", 0 Sres -> "go a b c d e" Sres StraySetNum "1 2 3 4 5", 0, 0 Sres -> "0 1 2 3 4 5" Srev StrayRev "a b c d e" Srev -> "e d c b a" Sub StraySub "a b c d e", 1, 3 Sub -> "b c" Sout StrayRmv "a b c d e", "b d" Sout -> "a c e" Srem StrayRemDup "a b a c c d e e" Srem -> "a b c d e" ift,iftlen StrayNumToFt "1 2 3 4 5", 1 ift -> 1 (same as f 1 0 -5 -2 1 2 3 4 5) iftlen -> 5
You can find an article about defining such a sub-language here, and the up to date UDO code here (or at the UDO repository).
Filter implementation via Sample-by-Sample Processing
At the end of chapter 03A the ability of sample-by-sample processing has been shown at some basic examples. This feature is really substaintial for writing digital filters. This can perfectly be done in the Csound language itself. The next example shows an implementation of the zero delay state variable filter by Steven Yi. In his collection at www.github.com/kunstmusik/libsyi more details and other implementaions can be found. — Note also that this code is an example of overloading a UDO definition. The same opcode name is defined here twice; first with the input types aKK (one audio signal and two k-signals with initialization), then with the input types aaa. This gives the user the possibility to use either of them with the same opcode name. Depending on the input, Csound will look for the proper implementation.
EXAMPLE 03G14_UDO_zdf_svf.csd
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
opcode zdf_svf,aaa,aKK
ain, kcf, kR xin
; pre-warp the cutoff- these are bilinear-transform filters
kwd = 2 * $M_PI * kcf
iT = 1/sr
kwa = (2/iT) * tan(kwd * iT/2)
kG = kwa * iT/2
;; output signals
alp init 0
ahp init 0
abp init 0
;; state for integrators
kz1 init 0
kz2 init 0
;;
kindx = 0
while kindx < ksmps do
khp = (ain[kindx] - (2 * kR + kG) * kz1 - kz2) / (1 + (2 * kR * kG) + (kG * kG))
kbp = kG * khp + kz1
klp = kG * kbp + kz2
; z1 register update
kz1 = kG * khp + kbp
kz2 = kG * kbp + klp
alp[kindx] = klp
ahp[kindx] = khp
abp[kindx] = kbp
kindx += 1
od
xout alp, abp, ahp
endop
opcode zdf_svf,aaa,aaa
ain, acf, aR xin
iT = 1/sr
;; output signals
alp init 0
ahp init 0
abp init 0
;; state for integrators
kz1 init 0
kz2 init 0
;;
kindx = 0
while kindx < ksmps do
; pre-warp the cutoff- these are bilinear-transform filters
kwd = 2 * $M_PI * acf[kindx]
kwa = (2/iT) * tan(kwd * iT/2)
kG = kwa * iT/2
kR = aR[kindx]
khp = (ain[kindx] - (2 * kR + kG) * kz1 - kz2) / (1 + (2 * kR * kG) + (kG * kG))
kbp = kG * khp + kz1
klp = kG * kbp + kz2
; z1 register update
kz1 = kG * khp + kbp
kz2 = kG * kbp + klp
alp[kindx] = klp
ahp[kindx] = khp
abp[kindx] = kbp
kindx += 1
od
xout alp, abp, ahp
endop
giSine ftgen 0, 0, 2^14, 10, 1
instr 1 ;only a dummy - will be replaced soon
aBuzz buzz 1, 100, 50, giSine
aLp, aBp, aHp zdf_svf aBuzz, 1000, 1
out aHp, aHp
endin
</CsInstruments>
<CsScore>
i 1 0 10
</CsScore>
</CsoundSynthesizer>
;example by steven yi
Links And Related Opcodes
Links
This is the page in the Canonical Csound Reference Manual about the definition of UDOs.
The most important resource of User Defined Opcodes is the User-Defined Opcode Database, editied by Steven Yi.
Also by Steven Yi, read the second part of his article about control flow in Csound in the Csound Journal (summer 2006).
Related Opcodes
opcode: The opcode used to begin a User Defined Opcode definition.
#include: Useful to include any loadable Csound code, in this case definitions of User Defined Opcodes.
setksmps: Lets you set a smaller ksmps value locally in a User Defined Opcode.
- Only the FLTK and STK opcodes begin with capital letters.^
- See https://github.com/joachimheintz/judo for more and more recent versions.^
MACROS
Macros within Csound provide a mechanism whereby a line or a block of code can be referenced using a macro codeword. Whenever the user-defined macro codeword for that block of code is subsequently encountered in a Csound orchestra or score it will be replaced by the code text contained within the macro. This mechanism can be extremely useful in situations where a line or a block of code will be repeated many times - if a change is required in the code that will be repeated, it need only be altered once in the macro definition rather than having to be edited in each of the repetitions.
Csound utilises a subtly different mechanism for orchestra and score macros so each will be considered in turn. There are also additional features offered by the macro system such as the ability to create a macro that accepts arguments - which can be thought of as the main macro containing sub-macros that can be repeated multiple times within the main macro - the inclusion of a block of text contained within a completely separate file and other macro refinements.
It is important to realise that a macro can contain any text, including carriage returns, and that Csound will be ignorant to its use of syntax until the macro is actually used and expanded elsewhere in the orchestra or score. Macro expansion is a feature of the orchestra and score parser and is not part of the orchestra performance time.
Orchestra Macros
Macros are defined using the syntax:
#define NAME # replacement text #
'NAME' is the user-defined name that will be used to call the macro at some point later in the orchestra; it must begin with a letter but can then contain any combination of numbers and letters. A limited range of special characters can be employed in the name. Apostrophes, hash symbols and dollar signs should be avoided. 'replacement text', bounded by hash symbols will be the text that will replace the macro name when later called. Remember that the replacement text can stretch over several lines. A macro can be defined anywhere within the <CsInstruments> </CsInstruments> sections of a .csd file. A macro can be redefined or overwritten by reusing the same macro name in another macro definition. Subsequent expansions of the macro will then use the new version.
To expand the macro later in the orchestra the macro name needs to be preceded with a '$' symbol thus:
$NAME
The following example illustrates the basic syntax needed to employ macros. The name of a sound file is referenced twice in the score so it is defined as a macro just after the header statements. Instrument 1 derives the duration of the sound file and instructs instrument 2 to play a note for this duration. instrument 2 plays the sound file. The score as defined in the <CsScore> </CsScore> section only lasts for 0.01 seconds but the event_i statement in instrument 1 will extend this for the required duration. The sound file is a mono file so you can replace it with any other mono file or use the original one.
EXAMPLE 03H01_Macros_basic.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 16
nchnls = 1
0dbfs = 1
; define the macro
#define SOUNDFILE # "loop.wav" #
instr 1
; use an expansion of the macro in deriving the duration of the sound file
idur filelen $SOUNDFILE
event_i "i",2,0,idur
endin
instr 2
; use another expansion of the macro in playing the sound file
a1 diskin2 $SOUNDFILE,1
out a1
endin
</CsInstruments>
<CsScore>
i 1 0 0.01
e
</CsScore>
</CsoundSynthesizer>
; example written by Iain McCurdy
In more complex situations where we require slight variations, such as different constant values or different sound files in each reuse of the macro, we can use a macro with arguments. A macro's arguments are defined as a list of sub-macro names within brackets after the name of the primary macro with each macro argument being separated using an apostrophe as shown below.
#define NAME(Arg1'Arg2'Arg3...) # replacement text #
Arguments can be any text string permitted as Csound code, they should not be likened to opcode arguments where each must conform to a certain type such as i, k, a etc. Macro arguments are subsequently referenced in the macro text using their names preceded by a '$' symbol. When the main macro is called later in the orchestra its arguments are then replaced with the values or strings required. The Csound Reference Manual states that up to five arguments are permitted but this still refers to an earlier implementation and in fact many more are actually permitted.
In the following example a 6 partial additive synthesis engine with a percussive character is defined within a macro. Its fundamental frequency and the ratios of its six partials to this fundamental frequency are prescribed as macro arguments. The macro is reused within the orchestra twice to create two different timbres, it could be reused many more times however. The fundamental frequency argument is passed to the macro as p4 from the score.
EXAMPLE 03H02_Macro_6partials.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 16
nchnls = 1
0dbfs = 1
gisine ftgen 0,0,2^10,10,1
; define the macro
#define ADDITIVE_TONE(Frq'Ratio1'Ratio2'Ratio3'Ratio4'Ratio5'Ratio6) #
iamp = 0.1
aenv expseg 1,p3*(1/$Ratio1),0.001,1,0.001
a1 poscil iamp*aenv,$Frq*$Ratio1,gisine
aenv expseg 1,p3*(1/$Ratio2),0.001,1,0.001
a2 poscil iamp*aenv,$Frq*$Ratio2,gisine
aenv expseg 1,p3*(1/$Ratio3),0.001,1,0.001
a3 poscil iamp*aenv,$Frq*$Ratio3,gisine
aenv expseg 1,p3*(1/$Ratio4),0.001,1,0.001
a4 poscil iamp*aenv,$Frq*$Ratio4,gisine
aenv expseg 1,p3*(1/$Ratio5),0.001,1,0.001
a5 poscil iamp*aenv,$Frq*$Ratio5,gisine
aenv expseg 1,p3*(1/$Ratio6),0.001,1,0.001
a6 poscil iamp*aenv,$Frq*$Ratio6,gisine
a7 sum a1,a2,a3,a4,a5,a6
out a7
#
instr 1 ; xylophone
; expand the macro with partial ratios that reflect those of a xylophone
; the fundemental frequency macro argument (the first argument -
; - is passed as p4 from the score
$ADDITIVE_TONE(p4'1'3.932'9.538'16.688'24.566'31.147)
endin
instr 2 ; vibraphone
$ADDITIVE_TONE(p4'1'3.997'9.469'15.566'20.863'29.440)
endin
</CsInstruments>
<CsScore>
i 1 0 1 200
i 1 1 2 150
i 1 2 4 100
i 2 3 7 800
i 2 4 4 700
i 2 5 7 600
e
</CsScore>
</CsoundSynthesizer>
; example written by Iain McCurdy
Score Macros
Score macros employ a similar syntax. Macros in the score can be used in situations where a long string of p-fields are likely to be repeated or, as in the next example, to define a palette of score patterns that repeat but with some variation such as transposition. In this example two 'riffs' are defined which each employ two macro arguments: the first to define when the riff will begin and the second to define a transposition factor in semitones. These riffs are played back using a bass guitar-like instrument using the wgpluck2 opcode. Remember that mathematical expressions within the Csound score must be bound within square brackets [].
EXAMPLE 03H03_Score_macro.csd
<CsoundSynthesizer> <CsOptions> -odac </CsOptions> <CsInstruments> sr = 44100 ksmps = 16 nchnls = 1 0dbfs = 1 instr 1 ; bass guitar a1 wgpluck2 0.98, 0.4, cpsmidinn(p4), 0.1, 0.6 aenv linseg 1,p3-0.1,1,0.1,0 out a1*aenv endin </CsInstruments> <CsScore> ; p4 = pitch as a midi note number #define RIFF_1(Start'Trans) # i 1 [$Start ] 1 [36+$Trans] i 1 [$Start+1 ] 0.25 [43+$Trans] i 1 [$Start+1.25] 0.25 [43+$Trans] i 1 [$Start+1.75] 0.25 [41+$Trans] i 1 [$Start+2.5 ] 1 [46+$Trans] i 1 [$Start+3.25] 1 [48+$Trans] # #define RIFF_2(Start'Trans) # i 1 [$Start ] 1 [34+$Trans] i 1 [$Start+1.25] 0.25 [41+$Trans] i 1 [$Start+1.5 ] 0.25 [43+$Trans] i 1 [$Start+1.75] 0.25 [46+$Trans] i 1 [$Start+2.25] 0.25 [43+$Trans] i 1 [$Start+2.75] 0.25 [41+$Trans] i 1 [$Start+3 ] 0.5 [43+$Trans] i 1 [$Start+3.5 ] 0.25 [46+$Trans] # t 0 90 $RIFF_1(0 ' 0) $RIFF_1(4 ' 0) $RIFF_2(8 ' 0) $RIFF_2(12'-5) $RIFF_1(16'-5) $RIFF_2(20'-7) $RIFF_2(24' 0) $RIFF_2(28' 5) e </CsScore> </CsoundSynthesizer> ; example written by Iain McCurdy
Score macros can themselves contain macros so that, for example, the above example could be further expanded so that a verse, chorus structure could be employed where verses and choruses, defined using macros, were themselves constructed from a series of riff macros.
UDOs and macros can both be used to reduce code repetition and there are many situations where either could be used with equal justification but each offers its own strengths. UDOs strengths lies in their ability to be used just like an opcode with inputs and outputs, the ease with which they can be shared - between Csound projects and between Csound users - their ability to operate at a different k-rate to the rest of the orchestra and in how they facilitate recursion. The fact that macro arguments are merely blocks of text, however, offers up new possibilities and unlike UDOs, macros can span several instruments. Of course UDOs have no use in the Csound score unlike macros. Macros can also be used to simplify the creation of complex FLTK GUI where panel sections might be repeated with variations of output variable names and location.
Csound's orchestra and score macro system offers many additional refinements and this chapter serves merely as an introduction to their basic use. To learn more it is recommended to refer to the relevant sections of the Csound Reference Manual.
FUNCTIONAL SYNTAX
Functional syntax is very common in many programming languages. It takes the form of fun(), where fun is any function which encloses its arguments in parentheses. Even in "old" Csound, there existed some rudiments of this functional syntax in some mathematical functions, such as sqrt(), log(), int(), frac(). For instance, the following code
iNum = 1.234 print int(iNum) print frac(iNum)
would print:
instr 1: #i0 = 1.000
instr 1: #i1 = 0.230
Here the integer part and the fractional part of the number 1.234 are passed directly as an argument to the print opcode, without needing to be stored at any point as a variable.
This alternative way of formulating code can now be used with many opcodes in Csound61. In the future many more opcodes will be incorporated into this system. First we shall look at some examples.
The traditional way of applying a fade and a sliding pitch (glissando) to a tone is something like this:
EXAMPLE 03I01_traditional_syntax.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
nchnls = 1
ksmps = 32
0dbfs = 1
instr 1
kFade linseg 0, p3/2, 1, p3/2, 0
kSlide expseg 400, p3/2, 800, p3/2, 600
aTone poscil kFade, kSlide
out aTone
endin
</CsInstruments>
<CsScore>
i 1 0 5
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
In plain English what is happening is:
- We create a line signal with the opcode linseg. It starts at zero, moves to one in half of the instrument's duration (p3/2), and moves back to zero for the second half of the instrument's duration. We store this signal in the variable kFade.
- We create an exponential2 signal with the opcode expseg. It starts at 400, moves to 800 in half the instrument's duration, and moves to 600 for the second half of the instrument's duration. We store this signal in the variable kSlide.
- We create a sine audio signal with the opcode poscil. We feed in the signal stored in the variable kFade as amplitude, and the signal stored in the variable kSlide as frequency input. We store the audio signal in the variable aTone.
- Finally, we write the audio signal to the output with the opcode out.
Each of these four lines can be considered as a "function call", as we call the opcodes (functions) linseg, expseg, poscil and out with certain arguments (input parameters). If we now transform this example to functional syntax, we will avoid storing the result of a function call in a variable. Rather we will feed the function and its arguments directly into the appropriate slot, by means of the fun() syntax.
If we write the first line in functional syntax, it will look like this:
linseg(0, p3/2, 1, p3/2, 0)
And the second line will look like this:
expseg(400, p3/2, 800, p3/2, 600)
So we can reduce our code from four lines to two lines:
EXAMPLE 03I02_functional_syntax_1.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
nchnls = 1
ksmps = 32
0dbfs = 1
instr 1
aTone poscil linseg(0, p3/2, 1, p3/2, 0), expseg(400, p3/2, 800, p3/2, 600)
out aTone
endin
</CsInstruments>
<CsScore>
i 1 0 5
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Or would you prefer the "all-in-one" solution?
EXAMPLE 03I03_functional_syntax_2.csd
<CsoundSynthesizer> <CsOptions> -odac </CsOptions> <CsInstruments> sr = 44100 nchnls = 1 ksmps = 32 0dbfs = 1 instr 1 out poscil(linseg(0, p3/2, 1, p3/2, 0), expseg(400, p3/2, 800, p3/2, 600)) endin </CsInstruments> <CsScore> i 1 0 5 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
Declare your color: i, k or a?
Most of the Csound opcodes work not only at one rate. You can, for instance, produce random numbers at i-, k- or a-rate:3
ires random imin, imax kres random kmin, kmax ares random kmin, kmax
Let us assume we want to change the highest frequency in our example from 800 to a random value between 700 and 1400 Hz, so that we hear a different movement for each tone. In this case, we can simply write random(700, 1400), because the context demands an i-rate result of the random operation here:4
EXAMPLE 03I04_functional_syntax_rate_1.csd
<CsoundSynthesizer> <CsOptions> -odac </CsOptions> <CsInstruments> sr = 44100 nchnls = 1 ksmps = 32 0dbfs = 1 instr 1 out poscil(linseg(0, p3/2, 1, p3/2, 0), expseg(400, p3/2, random(700, 1400), p3/2, 600)) endin </CsInstruments> <CsScore> r 5 i 1 0 3 </CsScore> </CsoundSynthesizer> ;example by joachim heintzBut it is much clearer both, for the Csound parser and for the Csound user, if you explicitly declare at which rate a function is to be performed. This code claims that poscil runs at a-rate, linseg and expseg run at k-rate, and random runs at i-rate here:
EXAMPLE 03I05_functional_syntax_rate_2.csd
<CsoundSynthesizer> <CsOptions> -odac </CsOptions> <CsInstruments> sr = 44100 nchnls = 1 ksmps = 32 0dbfs = 1 instr 1 out poscil:a(linseg:k(0, p3/2, 1, p3/2, 0), expseg:k(400, p3/2, random:i(700, 1400), p3/2, 600)) endin </CsInstruments> <CsScore> r 5 i 1 0 3 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
As you can see, rate declaration is done with simply :a, :k or :i after the function. It would represent good practice to include it all the time, to be clear about what is happening.
Only one output
Currently, there is a limitation in that only opcodes which have one or no outputs can be written using functional syntax. For instance, reading a stereo file using soundin
aL, aR soundin "my_file.wav"
cannot be written using functional syntax. This limitation is likely to be removed in the future.
fun() with UDOs
It should be mentioned that you can use the functional style also with self created opcodes ("User Defined Opcodes"):
EXAMPLE 03I06_functional_syntax_udo.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
nchnls = 1
ksmps = 32
0dbfs = 1
opcode FourModes, a, akk[]
;kFQ[] contains four frequency-quality pairs
aIn, kBasFreq, kFQ[] xin
aOut1 mode aIn, kBasFreq*kFQ[0], kFQ[1]
aOut2 mode aIn, kBasFreq*kFQ[2], kFQ[3]
aOut3 mode aIn, kBasFreq*kFQ[4], kFQ[5]
aOut4 mode aIn, kBasFreq*kFQ[6], kFQ[7]
xout (aOut1+aOut2+aOut3+aOut4) / 4
endop
instr 1
kArr[] fillarray 1, 2000, 2.8, 2000, 5.2, 2000, 8.2, 2000
aImp mpulse .3, 1
out FourModes(aImp, 200, kArr)
endin
</CsInstruments>
<CsScore>
i 1 0 10
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz, based on an example of iain mccurdy
How much fun() is good for you?
Only you, and perhaps your spiritual consultant, can know ...
But seriously, this is mostly a matter of style. Some people consider it most elegant if all is written in one single expression, whilst others prefer to see the signal flow from line to line. Certainly excessive numbers of parentheses may not result in the best looking code ...
At least the functional syntax allows the user to emphasize his or her own personal style and to avoid some awkwardness:
"If i new value of kIn has been received, do this and that", can be written:
if changed(kIn)==1 then <do this and that> endif
"If you understand what happens here, you will have been moved to the next level", can be written:
EXAMPLE 03I07_functional_syntax_you_win.csd
<CsoundSynthesizer>
<CsOptions>
-odac -m128
</CsOptions>
<CsInstruments>
sr = 44100
nchnls = 1
ksmps = 32
0dbfs = 1
seed 0
opcode FourModes, a, akk[]
;kFQ[] contains four frequency-quality pairs
aIn, kBasFreq, kFQ[] xin
aOut1 mode aIn, kBasFreq*kFQ[0], kFQ[1]
aOut2 mode aIn, kBasFreq*kFQ[2], kFQ[3]
aOut3 mode aIn, kBasFreq*kFQ[4], kFQ[5]
aOut4 mode aIn, kBasFreq*kFQ[6], kFQ[7]
xout (aOut1+aOut2+aOut3+aOut4) / 4
endop
instr ham
gkPchMovement = randomi:k(50, 1000, (random:i(.2, .4)), 3)
schedule("hum", 0, p3)
endin
instr hum
if metro(randomh:k(1, 10, random:k(1, 4), 3)) == 1 then
event("i", "play", 0, 5, gkPchMovement)
endif
endin
instr play
iQ1 = random(100, 1000)
kArr[] fillarray 1*random:i(.9, 1.1), iQ1,
2.8*random:i(.8, 1.2), iQ1*random:i(.5, 2),
5.2*random:i(.7, 1.4), iQ1*random:i(.5, 2),
8.2*random:i(.6, 1.8), iQ1*random:i(.5, 2)
aImp mpulse ampdb(random:k(-30, 0)), p3
out FourModes(aImp, p4, kArr)*linseg(1, p3/2, 1, p3/2, 0)
endin
</CsInstruments>
<CsScore>
i "ham" 0 60
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz, with thanks to steven and iain
So enjoy, and stay in contact with the spirit ...
- thanks to the huge work of John ffitch, Steven Yi and others on a new parser^
- which in simple words means that the signal moves like a curve which coincidents with the way we perceive frequency relations^
- See chapter 03A Initialization and Performance Pass for a more thorough explanation.^
- because all inputs for expseg must be i-rate^
04 SOUND SYNTHESIS
Csound: AdditiveSynthesis
ADDITIVE SYNTHESIS
Jean Baptiste Joseph Fourier demonstrated in around 1800 that any continuous function can be described perfectly as a sum of sine waves. This means that you can create any sound, no matter how complex, if you know how many sine waves, and at what frequencies, to add together.
This concept really excited the early pioneers of electronic music, who imagined that sine waves would give them the power to create any sound imaginable and previously unimagined sounds. Unfortunately, they soon realised that while adding sine waves is easy, interesting sounds require a large number of sine waves that are varying constantly in frequency and amplitude and this turns out to be a hugely impractical task.
Nonetheless, additive synthesis can provide unusual and interesting sounds and the power of modern computers and their ability to manage data in a programming language offers new dimensions of working with this old technique. As with most things in Csound there are several ways to go about implementing additive synthesis. We shall endeavour to introduce some of them and to allude to how they relate to different programming paradigms.
What are the Main Parameters of Additive Synthesis?
Before examining various methods of implementing additive synthesis in Csound, we shall first consider what parameters might be required. As additive synthesis involves the addition of multiple sine generators, the parameters we use will operate on one of two different levels:
- For each sine, there will be a frequency and an amplitude with an envelope.
- The frequency will usually be a constant value, but it can be varied and in fact natural sounds typically exhibit slight modulations of partial frequencies.
- The amplitude must have at least a simple envelope such as the well-known ADSR but more complex methods of continuously altering the amplitude will result in a livelier sound.
- For the sound as an entirety, the relevant parameters are:
- The total number of sinusoids. A sound which consists of just three sinusoids will most likely sound poorer than one which employs 100.
- The frequency ratios of the sine generators. For a classic harmonic spectrum, the multipliers of the sinusoids are 1, 2, 3, ... (If your first sine is 100 Hz, the others will be 200, 300, 400, ... Hz.) An inharmonic or noisy spectrum will probably have no simple integer ratios. These frequency ratios are chiefly responsible for our perception of timbre.
- The base frequency is the frequency of the first partial. If the partials are exhibiting a harmonic ratio, this frequency (in the example given 100 Hz) is also the overall perceived pitch.
- The amplitude ratios of the sinusoids. This is also very important in determining the resulting timbre of a sound. If the higher partials are relatively strong, the sound will be perceived as being more 'brilliant'; if the higher partials are soft, then the sound will be perceived as being dark and soft.
- The duration ratios of the sinusoids. In simple additive synthesis, all single sines have the same duration, but it will be more interesting if they differ - this will usually relate to the durations of the envelopes: if the envelopes of different partials vary, some partials will die away faster than others.
It is not always the aim of additive synthesis to imitate natural sounds, but the task of first analysing and then attempting to imitate a sound can prove to be very useful when studying additive synthesis. This is what a guitar note looks like when spectrally analysed:
Spectral analysis of a guitar tone in time (courtesy of W. Fohl, Hamburg)
Each partial possesses its own frequency movement and duration. We may or may not be able to achieve this successfully using additive synthesis. Let us begin with some simple sounds and consider how to go about programming this in Csound. Later we will look at some more complex sounds and the more advanced techniques required to synthesize them.
Simple Additions of Sinusoids Inside an Instrument
If additive synthesis amounts to simply adding together sine generators, it is therefore straightforward to implement this by creating multiple oscillators in a single instrument and adding their outputs together. In the following example, instrument 1 demonstrates the creation of a harmonic spectrum, and instrument 2 an inharmonic one. Both instruments share the same amplitude multipliers: 1, 1/2, 1/3, 1/4, ... and receive the base frequency in Csound's pitch notation (octave.semitone) and the main amplitude in dB.
EXAMPLE 04A01_AddSynth_simple.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;example by Andrés Cabrera
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
instr 1 ;harmonic additive synthesis
;receive general pitch and volume from the score
ibasefrq = cpspch(p4) ;convert pitch values to frequency
ibaseamp = ampdbfs(p5) ;convert dB to amplitude
;create 8 harmonic partials
aOsc1 poscil ibaseamp, ibasefrq, giSine
aOsc2 poscil ibaseamp/2, ibasefrq*2, giSine
aOsc3 poscil ibaseamp/3, ibasefrq*3, giSine
aOsc4 poscil ibaseamp/4, ibasefrq*4, giSine
aOsc5 poscil ibaseamp/5, ibasefrq*5, giSine
aOsc6 poscil ibaseamp/6, ibasefrq*6, giSine
aOsc7 poscil ibaseamp/7, ibasefrq*7, giSine
aOsc8 poscil ibaseamp/8, ibasefrq*8, giSine
;apply simple envelope
kenv linen 1, p3/4, p3, p3/4
;add partials and write to output
aOut = aOsc1 + aOsc2 + aOsc3 + aOsc4 + aOsc5 + aOsc6 + aOsc7 + aOsc8
outs aOut*kenv, aOut*kenv
endin
instr 2 ;inharmonic additive synthesis
ibasefrq = cpspch(p4)
ibaseamp = ampdbfs(p5)
;create 8 inharmonic partials
aOsc1 poscil ibaseamp, ibasefrq, giSine
aOsc2 poscil ibaseamp/2, ibasefrq*1.02, giSine
aOsc3 poscil ibaseamp/3, ibasefrq*1.1, giSine
aOsc4 poscil ibaseamp/4, ibasefrq*1.23, giSine
aOsc5 poscil ibaseamp/5, ibasefrq*1.26, giSine
aOsc6 poscil ibaseamp/6, ibasefrq*1.31, giSine
aOsc7 poscil ibaseamp/7, ibasefrq*1.39, giSine
aOsc8 poscil ibaseamp/8, ibasefrq*1.41, giSine
kenv linen 1, p3/4, p3, p3/4
aOut = aOsc1 + aOsc2 + aOsc3 + aOsc4 + aOsc5 + aOsc6 + aOsc7 + aOsc8
outs aOut*kenv, aOut*kenv
endin
</CsInstruments>
<CsScore>
; pch amp
i 1 0 5 8.00 -13
i 1 3 5 9.00 -17
i 1 5 8 9.02 -15
i 1 6 9 7.01 -15
i 1 7 10 6.00 -13
s
i 2 0 5 8.00 -13
i 2 3 5 9.00 -17
i 2 5 8 9.02 -15
i 2 6 9 7.01 -15
i 2 7 10 6.00 -13
</CsScore>
</CsoundSynthesizer>
Simple Additions of Sinusoids via the Score
A typical paradigm in programming: if you are repeating lines of code with just minor variations, consider abstracting it in some way. In the Csound language this could mean moving parameter control to the score. In our case, the lines
aOsc1 poscil ibaseamp, ibasefrq, giSine aOsc2 poscil ibaseamp/2, ibasefrq*2, giSine aOsc3 poscil ibaseamp/3, ibasefrq*3, giSine aOsc4 poscil ibaseamp/4, ibasefrq*4, giSine aOsc5 poscil ibaseamp/5, ibasefrq*5, giSine aOsc6 poscil ibaseamp/6, ibasefrq*6, giSine aOsc7 poscil ibaseamp/7, ibasefrq*7, giSine aOsc8 poscil ibaseamp/8, ibasefrq*8, giSine
could be abstracted to the form
aOsc poscil ibaseamp*iampfactor, ibasefrq*ifreqfactor, giSine
with the parameters iampfactor (the relative amplitude of a partial) and ifreqfactor (the frequency multiplier) being transferred to the score as p-fields.
The next version of the previous instrument, simplifies the instrument code and defines the variable values as score parameters:
EXAMPLE 04A02_AddSynth_score.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;example by Andrés Cabrera and Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
instr 1
iBaseFreq = cpspch(p4)
iFreqMult = p5 ;frequency multiplier
iBaseAmp = ampdbfs(p6)
iAmpMult = p7 ;amplitude multiplier
iFreq = iBaseFreq * iFreqMult
iAmp = iBaseAmp * iAmpMult
kEnv linen iAmp, p3/4, p3, p3/4
aOsc poscil kEnv, iFreq, giSine
outs aOsc, aOsc
endin
</CsInstruments>
<CsScore>
; freq freqmult amp ampmult
i 1 0 7 8.09 1 -10 1
i . . 6 . 2 . [1/2]
i . . 5 . 3 . [1/3]
i . . 4 . 4 . [1/4]
i . . 3 . 5 . [1/5]
i . . 3 . 6 . [1/6]
i . . 3 . 7 . [1/7]
s
i 1 0 6 8.09 1.5 -10 1
i . . 4 . 3.1 . [1/3]
i . . 3 . 3.4 . [1/6]
i . . 4 . 4.2 . [1/9]
i . . 5 . 6.1 . [1/12]
i . . 6 . 6.3 . [1/15]
</CsScore>
</CsoundSynthesizer>
You might ask: "Okay, where is the simplification? There are even more lines than before!" This is true, but this still represents better coding practice. The main benefit now is flexibility. Now we are able to realise any number of partials using the same instrument, with any amplitude, frequency and duration ratios. Using the Csound score abbreviations (for instance a dot for repeating the previous value in the same p-field), you can make great use of copy-and-paste, and focus just on what is changing from line to line.
Note that you are now calling one instrument multiple times in the creation of a single additive synthesis note, in fact, each instance of the instrument contributes just one partial to the additive tone. Calling multiple instances of one instrument in this way also represents good practice in Csound coding. We will discuss later how this end can be achieved in a more elegant way.
Creating Function Tables for Additive Synthesis
Before we continue, let us return to the first example and discuss a classic and abbreviated method for playing a number of partials. As we mentioned at the beginning, Fourier stated that any periodic oscillation can be described using a sum of simple sinusoids. If the single sinusoids are static (with no individual envelopes, durations or frequency fluctuations), the resulting waveform will be similarly static.
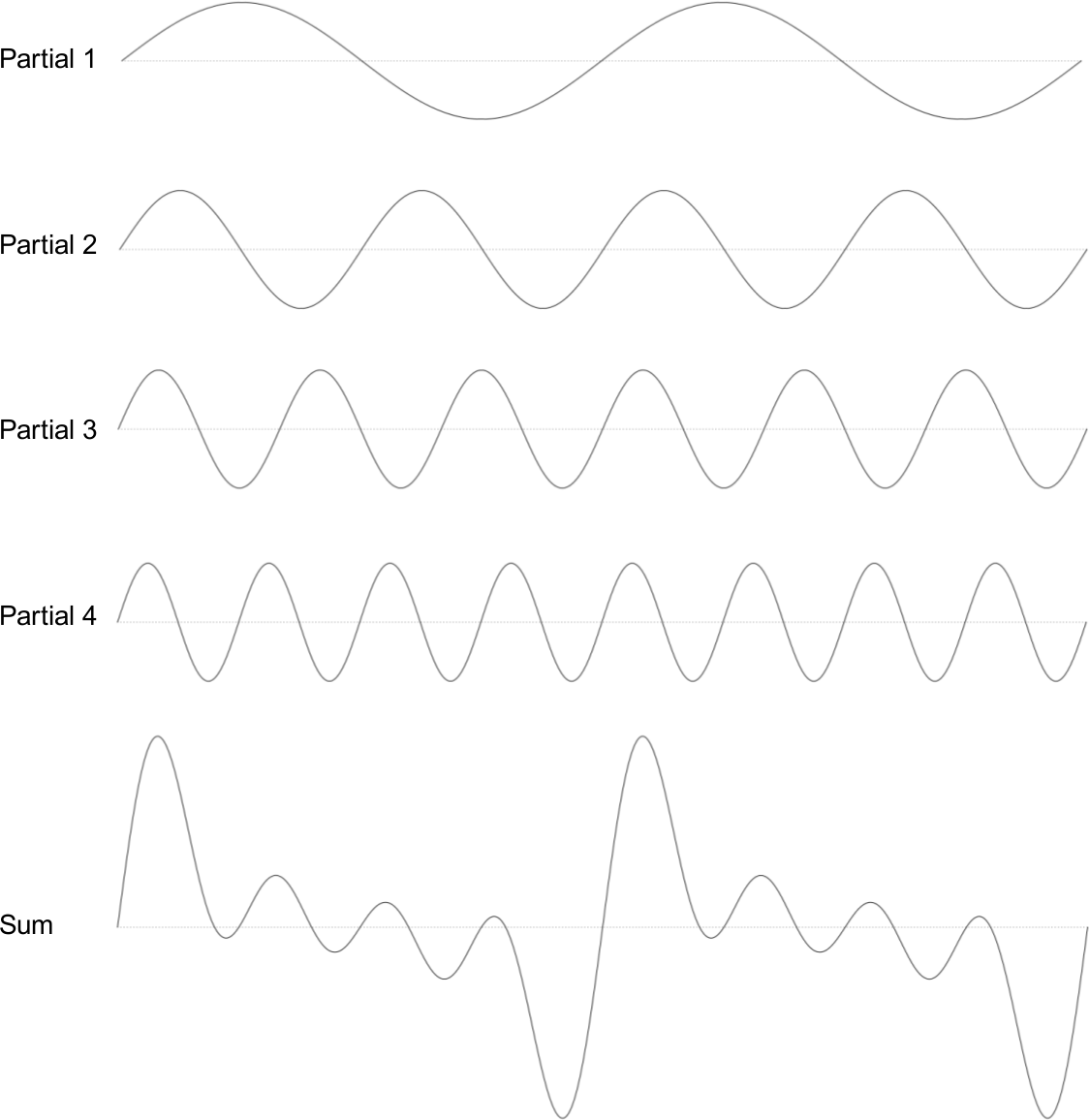
Above you see four sine waves, each with fixed frequency and amplitude relationships. These are then mixed together with the resulting waveform illustrated at the bottom (Sum). This then begs the question: why not simply calculate this composite waveform first, and then read it with just a single oscillator?
This is what some Csound GEN routines do. They compose the resulting shape of the periodic waveform, and store the values in a function table. GEN10 can be used for creating a waveform consisting of harmonically related partials. It form begins with the common GEN routine p-fields
<table number>, <creation time>, <size in points>, <GEN number>
following which you just have to define the relative strengths of the harmonics. GEN09 is more complex and allows you to also control the frequency multiplier and the phase (0-360°) of each partial. Thus we are able to reproduce the first example in a shorter (and computationally faster) form:
EXAMPLE 04A03_AddSynth_GEN.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;example by Andrés Cabrera and Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
giHarm ftgen 1, 0, 2^12, 10, 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8
giNois ftgen 2, 0, 2^12, 9, 100,1,0, 102,1/2,0, 110,1/3,0, \
123,1/4,0, 126,1/5,0, 131,1/6,0, 139,1/7,0, 141,1/8,0
instr 1
iBasFreq = cpspch(p4)
iTabFreq = p7 ;base frequency of the table
iBasFreq = iBasFreq / iTabFreq
iBaseAmp = ampdb(p5)
iFtNum = p6
aOsc poscil iBaseAmp, iBasFreq, iFtNum
aEnv linen aOsc, p3/4, p3, p3/4
outs aEnv, aEnv
endin
</CsInstruments>
<CsScore>
; pch amp table table base (Hz)
i 1 0 5 8.00 -10 1 1
i . 3 5 9.00 -14 . .
i . 5 8 9.02 -12 . .
i . 6 9 7.01 -12 . .
i . 7 10 6.00 -10 . .
s
i 1 0 5 8.00 -10 2 100
i . 3 5 9.00 -14 . .
i . 5 8 9.02 -12 . .
i . 6 9 7.01 -12 . .
i . 7 10 6.00 -10 . .
</CsScore>
</CsoundSynthesizer>
You maybe noticed that to store a waveform in which the partials are not harmonically related, the table must be constructed in a slightly special way (see table 'giNois'). If the frequency multipliers in our first example started with 1 and 1.02, the resulting period is actually very long. If the oscillator was playing at 100 Hz, the tone it would produce would actually contain partials at 100 Hz and 102 Hz. So you need 100 cycles from the 1.00 multiplier and 102 cycles from the 1.02 multiplier to complete one period of the composite waveform. In other words, we have to create a table which contains respectively 100 and 102 periods, instead of 1 and 1.02. Therefore the table frequencies will not be related to 1 as usual but instead to 100. This is the reason that we have to introduce a new parameter, iTabFreq, for this purpose. (N.B. In this simple example we could actually reduce the ratios to 50 and 51 as 100 and 102 share a common denominator of 2.)
This method of composing waveforms can also be used for generating four standard waveform shapes typically encountered in vintage synthesizers. An impulse wave can be created by adding a number of harmonics of the same strength. A sawtooth wave has the amplitude multipliers 1, 1/2, 1/3, ... for the harmonics. A square wave has the same multipliers, but just for the odd harmonics. A triangle can be calculated as 1 divided by the square of the odd partials, with swapping positive and negative values. The next example creates function tables with just the first ten partials for each of these waveforms.
EXAMPLE 04A04_Standard_waveforms.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giImp ftgen 1, 0, 4096, 10, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1
giSaw ftgen 2, 0, 4096, 10, 1,1/2,1/3,1/4,1/5,1/6,1/7,1/8,1/9,1/10
giSqu ftgen 3, 0, 4096, 10, 1, 0, 1/3, 0, 1/5, 0, 1/7, 0, 1/9, 0
giTri ftgen 4, 0, 4096, 10, 1, 0, -1/9, 0, 1/25, 0, -1/49, 0, 1/81, 0
instr 1
asig poscil .2, 457, p4
outs asig, asig
endin
</CsInstruments>
<CsScore>
i 1 0 3 1
i 1 4 3 2
i 1 8 3 3
i 1 12 3 4
</CsScore>
</CsoundSynthesizer>
Triggering Instrument Events for the Partials
Performing additive synthesis by designing partial strengths into function tables has the disadvantage that once a note has begun there is no way of varying the relative strengths of individual partials. There are various methods to circumvent the inflexibility of table-based additive synthesis such as morphing between several tables (for example by using the ftmorf opcode) or by filtering the result. Next we shall consider another approach: triggering one instance of a sub-instrument1 for each partial, and exploring the possibilities of creating a spectrally dynamic sound using this technique.
Let us return to the second instrument (04A02.csd) which had already made use of some abstractions and triggered one instrument instance for each partial. This was done in the score, but now we will trigger one complete note in one score line, not just one partial. The first step is to assign the desired number of partials via a score parameter. The next example triggers any number of partials using this one value:
EXAMPLE 04A05_Flexible_number_of_partials.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
instr 1 ;master instrument
inumparts = p4 ;number of partials
ibasfreq = 200 ;base frequency
ipart = 1 ;count variable for loop
;loop for inumparts over the ipart variable
;and trigger inumpartss instanes of the subinstrument
loop:
ifreq = ibasfreq * ipart
iamp = 1/ipart/inumparts
event_i "i", 10, 0, p3, ifreq, iamp
loop_le ipart, 1, inumparts, loop
endin
instr 10 ;subinstrument for playing one partial
ifreq = p4 ;frequency of this partial
iamp = p5 ;amplitude of this partial
aenv transeg 0, .01, 0, iamp, p3-0.1, -10, 0
apart poscil aenv, ifreq, giSine
outs apart, apart
endin
</CsInstruments>
<CsScore>
; number of partials
i 1 0 3 10
i 1 3 3 20
i 1 6 3 2
</CsScore>
</CsoundSynthesizer>
This instrument can easily be transformed to be played via a midi keyboard. In the next the midi key velocity will map to the number of synthesized partials played to implement a brightness control.
EXAMPLE 04A06_Play_it_with_Midi.csd
<CsoundSynthesizer>
<CsOptions>
-o dac -Ma
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
massign 0, 1 ;all midi channels to instr 1
instr 1 ;master instrument
ibasfreq cpsmidi ;base frequency
iampmid ampmidi 20 ;receive midi-velocity and scale 0-20
inparts = int(iampmid)+1 ;exclude zero
ipart = 1 ;count variable for loop
;loop for inparts over the ipart variable
;and trigger inparts instances of the sub-instrument
loop:
ifreq = ibasfreq * ipart
iamp = 1/ipart/inparts
event_i "i", 10, 0, 1, ifreq, iamp
loop_le ipart, 1, inparts, loop
endin
instr 10 ;subinstrument for playing one partial
ifreq = p4 ;frequency of this partial
iamp = p5 ;amplitude of this partial
aenv transeg 0, .01, 0, iamp, p3-.01, -3, 0
apart poscil aenv, ifreq, giSine
outs apart/3, apart/3
endin
</CsInstruments>
<CsScore>
f 0 3600
</CsScore>
</CsoundSynthesizer>
Although this instrument is rather primitive it is useful to be able to control the timbre in this way using key velocity. Let us continue to explore some other methods of creating parameter variation in additive synthesis.
User-controlled Random Variations in Additive Synthesis
Natural sounds exhibit constant movement and change in the parameters we have so far discussed. Even the best player or singer will not be able to play a note in the exact same way twice and within a tone, the partials will have some unsteadiness: slight waverings in the amplitudes and slight frequency fluctuations. In an audio programming environment like Csound, we can imitate these movements by employing random deviations. The boundaries of random deviations must be adjusted as carefully. Exaggerate them and the result will be unnatural or like a bad player. The rates or speeds of these fluctuations will also need to be chosen carefully and sometimes we need to modulate the rate of modulation in order to achieve naturalness.
Let us start with some random deviations in our subinstrument. The following parameters can be affected:
- The frequency of each partial can be slightly detuned. The range of this possible maximum detuning can be set in cents (100 cent = 1 semitone).
- The amplitude of each partial can be altered relative to its default value. This alteration can be measured in decibels (dB).
- The duration of each partial can be made to be longer or shorter than the default value. Let us define this deviation as a percentage. If the expected duration is five seconds, a maximum deviation of 100% will mean a resultant value of between half the duration (2.5 sec) and double the duration (10 sec).
The following example demonstrates the effect of these variations. As a base - and as a reference to its author - we take as our starting point, the 'bell-like' sound created by Jean-Claude Risset in his 'Sound Catalogue'.2
EXAMPLE 04A07_Risset_variations.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
;frequency and amplitude multipliers for 11 partials of Risset's bell
giFqs ftgen 0, 0, -11,-2,.56,.563,.92, .923,1.19,1.7,2,2.74, \
3,3.74,4.07
giAmps ftgen 0, 0, -11, -2, 1, 2/3, 1, 1.8, 8/3, 1.46, 4/3, 4/3, 1, 4/3
giSine ftgen 0, 0, 2^10, 10, 1
seed 0
instr 1 ;master instrument
ibasfreq = 400
ifqdev = p4 ;maximum freq deviation in cents
iampdev = p5 ;maximum amp deviation in dB
idurdev = p6 ;maximum duration deviation in %
indx = 0 ;count variable for loop
loop:
ifqmult tab_i indx, giFqs ;get frequency multiplier from table
ifreq = ibasfreq * ifqmult
iampmult tab_i indx, giAmps ;get amp multiplier
iamp = iampmult / 20 ;scale
event_i "i", 10, 0, p3, ifreq, iamp, ifqdev, iampdev, idurdev
loop_lt indx, 1, 11, loop
endin
instr 10 ;subinstrument for playing one partial
;receive the parameters from the master instrument
ifreqnorm = p4 ;standard frequency of this partial
iampnorm = p5 ;standard amplitude of this partial
ifqdev = p6 ;maximum freq deviation in cents
iampdev = p7 ;maximum amp deviation in dB
idurdev = p8 ;maximum duration deviation in %
;calculate frequency
icent random -ifqdev, ifqdev ;cent deviation
ifreq = ifreqnorm * cent(icent)
;calculate amplitude
idb random -iampdev, iampdev ;dB deviation
iamp = iampnorm * ampdb(idb)
;calculate duration
idurperc random -idurdev, idurdev ;duration deviation (%)
iptdur = p3 * 2^(idurperc/100)
p3 = iptdur ;set p3 to the calculated value
;play partial
aenv transeg 0, .01, 0, iamp, p3-.01, -10, 0
apart poscil aenv, ifreq, giSine
outs apart, apart
endin
</CsInstruments>
<CsScore>
; frequency amplitude duration
; deviation deviation deviation
; in cent in dB in %
;;unchanged sound (twice)
r 2
i 1 0 5 0 0 0
s
;;slight variations in frequency
r 4
i 1 0 5 25 0 0
;;slight variations in amplitude
r 4
i 1 0 5 0 6 0
;;slight variations in duration
r 4
i 1 0 5 0 0 30
;;slight variations combined
r 6
i 1 0 5 25 6 30
;;heavy variations
r 6
i 1 0 5 50 9 100
</CsScore>
</CsoundSynthesizer>
In midi-triggered descendant of this instrument, we could - as one of many possible options - vary the amount of possible random variation according to the key velocity so that a key pressed softly plays the bell-like sound as described by Risset but as a key is struck with increasing force the sound produced will be increasingly altered.
EXAMPLE 04A08_Risset_played_by_Midi.csd
<CsoundSynthesizer>
<CsOptions>
-o dac -Ma
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
;frequency and amplitude multipliers for 11 partials of Risset's bell
giFqs ftgen 0, 0, -11, -2, .56,.563,.92,.923,1.19,1.7,2,2.74,3,\
3.74,4.07
giAmps ftgen 0, 0, -11, -2, 1, 2/3, 1, 1.8, 8/3, 1.46, 4/3, 4/3, 1,\
4/3
giSine ftgen 0, 0, 2^10, 10, 1
seed 0
massign 0, 1 ;all midi channels to instr 1
instr 1 ;master instrument
;;scale desired deviations for maximum velocity
;frequency (cent)
imxfqdv = 100
;amplitude (dB)
imxampdv = 12
;duration (%)
imxdurdv = 100
;;get midi values
ibasfreq cpsmidi ;base frequency
iampmid ampmidi 1 ;receive midi-velocity and scale 0-1
;;calculate maximum deviations depending on midi-velocity
ifqdev = imxfqdv * iampmid
iampdev = imxampdv * iampmid
idurdev = imxdurdv * iampmid
;;trigger subinstruments
indx = 0 ;count variable for loop
loop:
ifqmult tab_i indx, giFqs ;get frequency multiplier from table
ifreq = ibasfreq * ifqmult
iampmult tab_i indx, giAmps ;get amp multiplier
iamp = iampmult / 20 ;scale
event_i "i", 10, 0, 3, ifreq, iamp, ifqdev, iampdev, idurdev
loop_lt indx, 1, 11, loop
endin
instr 10 ;subinstrument for playing one partial
;receive the parameters from the master instrument
ifreqnorm = p4 ;standard frequency of this partial
iampnorm = p5 ;standard amplitude of this partial
ifqdev = p6 ;maximum freq deviation in cents
iampdev = p7 ;maximum amp deviation in dB
idurdev = p8 ;maximum duration deviation in %
;calculate frequency
icent random -ifqdev, ifqdev ;cent deviation
ifreq = ifreqnorm * cent(icent)
;calculate amplitude
idb random -iampdev, iampdev ;dB deviation
iamp = iampnorm * ampdb(idb)
;calculate duration
idurperc random -idurdev, idurdev ;duration deviation (%)
iptdur = p3 * 2^(idurperc/100)
p3 = iptdur ;set p3 to the calculated value
;play partial
aenv transeg 0, .01, 0, iamp, p3-.01, -10, 0
apart poscil aenv, ifreq, giSine
outs apart, apart
endin
</CsInstruments>
<CsScore>
f 0 3600
</CsScore>
</CsoundSynthesizer>
Whether you can play examples like this in realtime will depend on the power of your computer. Have a look at chapter 2D (Live Audio) for tips on getting the best possible performance from your Csound orchestra.
In the next example we shall use additive synthesis to make a kind of a wobble bass. It starts as a bass sound, then evolves into something else, and then returns to being a bass sound again. We will first generate all the inharmonic partials with a loop. Harmonic partials are arithmetic, we add the same value to one partial to get the next. In this example we will instead use geometric partials, we will multiply one partial with a certain number (kfreqmult) to derive the next partial frequency and so on. This number will not be constant, but will be generated by a sine oscillator. This is frequency modulation. Finally some randomness is added to create a more interesting sound, and a chorus effect is also added to make the sound more 'fat'. The exponential function, exp, is used when deriving frequencies because if we move upwards in common musical scales, then the frequencies grow exponentially.
EXAMPLE 04A09_Wobble_bass.csd
<CsoundSynthesizer> ; Wobble bass made using additive synthesis
<CsOptions> ; and frequency modulation
-odac
</CsOptions>
<CsInstruments>
; Example by Bjørn Houdorf, March 2013
sr = 44100
ksmps = 1
nchnls = 2
0dbfs = 1
instr 1
kamp = 24 ; Amplitude
kfreq expseg p4, p3/2, 50*p4, p3/2, p4 ; Base frequency
iloopnum = p5 ; Number of all partials generated
alyd1 init 0
alyd2 init 0
seed 0
kfreqmult oscili 1, 2, 1
kosc oscili 1, 2.1, 1
ktone randomh 0.5, 2, 0.2 ; A random input
icount = 1
loop: ; Loop to generate partials to additive synthesis
kfreq = kfreqmult * kfreq
atal oscili 1, 0.5, 1
apart oscili 1, icount*exp(atal*ktone) , 1 ; Modulate each partials
anum = apart*kfreq*kosc
asig1 oscili kamp, anum, 1
asig2 oscili kamp, 1.5*anum, 1 ; Chorus effect to make the sound more "fat"
asig3 oscili kamp, 2*anum, 1
asig4 oscili kamp, 2.5*anum, 1
alyd1 = (alyd1 + asig1+asig4)/icount ;Sum of partials
alyd2 = (alyd2 + asig2+asig3)/icount
loop_lt icount, 1, iloopnum, loop ; End of loop
outs alyd1, alyd2 ; Output generated sound
endin
</CsInstruments>
<CsScore>
f1 0 128 10 1
i1 0 60 110 50
e
</CsScore>
</CsoundSynthesizer>
gbuzz, buzz and GEN11
gbuzz is useful for creating additive tones made of harmonically related cosine waves. Rather than define attributes for every partial individually, gbuzz allows us to define parameters that describe the entire additive tone in a more general way: specifically the number of partials in the tone, the partial number of the lowest partial present and an amplitude coefficient multipler, which shifts the peak of spectral energy in the tone. Although number of harmonics (knh) and lowest hamonic (klh) are k-rate arguments, they are only interpreted as integers by the opcode; therefore changes from integer to integer will result in discontinuities in the output signal. The amplitude coefficient multiplier allows for smooth spectral modulations however. Although we lose some control of individual partials using gbuzz, we gain by being able to nimbly sculpt the spectrum of the tone it produces.
In the following example a 100Hz tone is created, in which the number of partials it contains rises from 1 to 20 across its 8 second duration. A spectrogram/sonogram displays how this manifests spectrally. A linear frequency scale is employed in the spectrogram so that harmonic partials appear equally spaced.
EXAMPLE 04A10_gbuzz.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
; a cosine wave
gicos ftgen 0, 0, 2^10, 11, 1
instr 1
knh line 1, p3, 20 ; number of harmonics
klh = 1 ; lowest harmonic
kmul = 1 ; amplitude coefficient multiplier
asig gbuzz 1, 100, knh, klh, kmul, gicos
outs asig, asig
endin
</CsInstruments>
<CsScore>
i 1 0 8
e
</CsScore>
</CsoundSynthesizer>
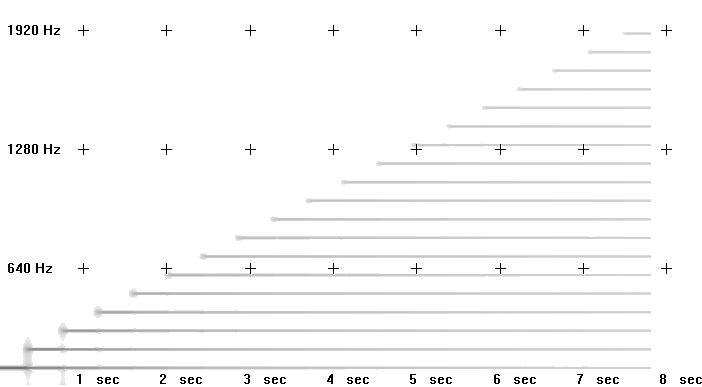
The total number of partials only reaches 19 because the line function only reaches 20 at the very conclusion of the note.
In the next example the number of partials contained within the tone remains constant but the partial number of the lowest partial rises from 1 to 20.
EXAMPLE 04A11_gbuzz_partials_rise.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
; a cosine wave
gicos ftgen 0, 0, 2^10, 11, 1
instr 1
knh = 20
klh line 1, p3, 20
kmul = 1
asig gbuzz 1, 100, knh, klh, kmul, gicos
outs asig, asig
endin
</CsInstruments>
<CsScore>
i 1 0 8
e
</CsScore>
</CsoundSynthesizer>
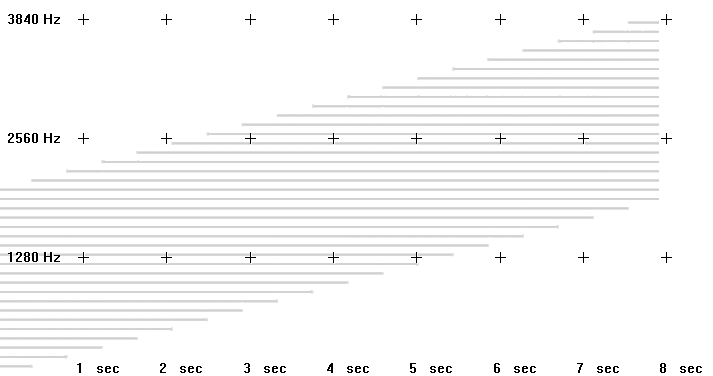
In the spectrogram it can be seen how, as lowermost partials are removed, additional partials are added at the top of the spectrum. This is because the total number of partials remains constant at 20.
In the final gbuzz example the amplitude coefficient multiplier rises from 0 to 2. It can be heard (and seen in the spectrogram) how, when this value is zero, emphasis is on the lowermost partial and when this value is 2, emphasis is on the uppermost partial.
EXAMPLE 04A12_gbuzz_amp_coeff_rise.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
; a cosine wave
gicos ftgen 0, 0, 2^10, 11, 1
instr 1
knh = 20
klh = 1
kmul line 0, p3, 2
asig gbuzz 1, 100, knh, klh, kmul, gicos
outs asig, asig
endin
</CsInstruments>
<CsScore>
i 1 0 8
e
</CsScore>
</CsoundSynthesizer>
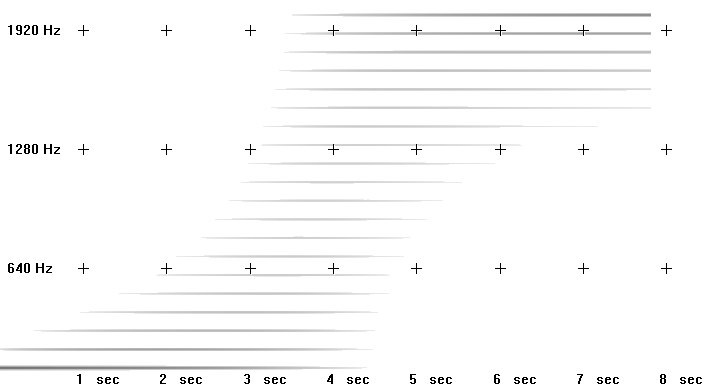
buzz is a simplified version of gbuzz with fewer parameters – it does not provide for modulation of the lowest partial number and amplitude coefficient multiplier.
GEN11 creates a function table waveform using the same parameters as gbuzz. If a gbuzz tone is required but no performance time modulation of its parameters is needed, GEN11 may provide a more efficient option. GEN11 also opens the possibility of using its waveforms in a variety of other opcodes. gbuzz, buzz and GEN11 may also prove useful as a source for subtractive synthesis.
Additional Interesting Opcodes for Additive Synthesis
hsboscil
The opcode hsboscil offers an interesting method of additive synthesis in which all partials are spaced an octave apart. Whilst this may at first seems limiting, it does offer simple means for morphing the precise make up of its spectrum. It can be thought of as producing a sound spectrum that extends infinitely above and below the base frequency. Rather than sounding all of the resultant partials simultaneously, a window (typically a Hanning window) is placed over the spectrum, masking it so that only one or several of these partials sound at any one time. The user can shift the position of this window up or down the spectrum at k-rate and this introduces the possibility of spectral morphing. hsbosil refers to this control as 'kbrite'. The width of the window can be specified (but only at i-time) using its 'iOctCnt' parameter. The entire spectrum can also be shifted up or down, independent of the location of the masking window using the 'ktone' parameter, which can be used to create a 'Risset glissando'-type effect. The sense of the interval of an octave between partials tends to dominate but this can be undermined through the use of frequency shifting or by using a waveform other than a sine wave as the source waveform for each partial.
In the next example, instrument 1 demonstrates the basic sound produced by hsboscil whilst randomly modulating the location of the masking window (kbrite) and the transposition control (ktone). Instrument 2 introduces frequency shifting (through the use of the hilbert opcode) which adds a frequency value to all partials thereby warping the interval between partials. Instrument 3 employs a more complex waveform (pseudo-inharmonic) as the source waveform for the partials.
EXAMPLE 04A13_hsboscil.csd
<CsoundSynthesizer>
<CsOptions>
--env:SSDIR+=../SourceMaterials -odac
</CsOptions>
<CsInstruments>
;example by iain mccurdy
sr = 44100
ksmps = 32
0dbfs = 1
nchnls = 2
giSine ftgen 0, 0, 2^10, 10, 1
; hanning window
giWindow ftgen 0, 0, 1024, -19, 1, 0.5, 270, 0.5
; a complex pseudo inharmonic waveform (partials scaled up X 100)
giWave ftgen 0, 0, 262144, 9, 100,1.000,0, 278,0.500,0, 518,0.250,0,
816,0.125,0, 1166,0.062,0, 1564,0.031,0, 1910,0.016,0
instr 1 ; demonstration of hsboscil
kAmp = 0.3
kTone rspline -1,1,0.05,0.2 ; randomly shift spectrum up and down
kBrite rspline -1,3,0.4,2 ; randomly shift masking window up and down
iBasFreq = 200 ; base frequency
iOctCnt = 3 ; width of masking window
aSig hsboscil kAmp, kTone, kBrite, iBasFreq, giSine, giWindow, iOctCnt
out aSig, aSig
endin
instr 2 ; frequency shifting added
kAmp = 0.3
kTone = 0 ; spectrum remains static this time
kBrite rspline -2,5,0.4,2 ; randomly shift masking window up and down
iBasFreq = 75 ; base frequency
iOctCnt = 6 ; width of masking window
aSig hsboscil kAmp, kTone, kBrite, iBasFreq, giSine, giWindow, iOctCnt
; frequency shift the sound
kfshift = -357 ; amount to shift the frequency
areal,aimag hilbert aSig ; hilbert filtering
asin poscil 1, kfshift, giSine, 0 ; modulating signals
acos poscil 1, kfshift, giSine, 0.25
aSig = (areal*acos) - (aimag*asin) ; frequency shifted signal
out aSig, aSig
endin
instr 3 ; hsboscil using a complex waveform
kAmp = 0.3
kTone rspline -1,1,0.05,0.2 ; randomly shift spectrum up and down
kBrite rspline -3,3,0.1,1 ; randomly shift masking window
iBasFreq = 200
aSig hsboscil kAmp, kTone, kBrite, iBasFreq/100, giWave, giWindow
aSig2 hsboscil kAmp,kTone, kBrite, (iBasFreq*1.001)/100, giWave, giWindow
out aSig+aSig2, aSig+aSig2 ; mix signal with 'detuned' version
endin
</CsInstruments>
<CsScore>
i 1 0 14
i 2 15 14
i 3 30 14
e
</CsScore>
</CsoundSynthesizer>
Additive synthesis can still be an exciting way of producing sounds. It offers the user a level of control that other methods of synthesis simply cannot match. It also provides an essential workbench for learning about acoustics and spectral theory as related to sound.
- This term is used here in a general manner. There is also a Csound opcode "subinstr", which has some more specific meanings. ^
- Jean-Claude Risset, Introductory Catalogue of Computer Synthesized Sounds (1969), cited after Dodge/Jerse, Computer Music, New York / London 1985, p.94^
Csound: SUBTRACTIVESYNTHESIS
SUBTRACTIVE SYNTHESIS
Introduction
Subtractive synthesis is, at least conceptually, the inverse of additive synthesis in that instead of building complex sound through the addition of simple cellular materials such as sine waves, subtractive synthesis begins with a complex sound source, such as white noise or a recorded sample, or a rich waveform, such as a sawtooth or pulse, and proceeds to refine that sound by removing partials or entire sections of the frequency spectrum through the use of audio filters.
The creation of dynamic spectra (an arduous task in additive synthesis) is relatively simple in subtractive synthesis as all that will be required will be to modulate a few parameters pertaining to any filters being used. Working with the intricate precision that is possible with additive synthesis may not be as easy with subtractive synthesis but sounds can be created much more instinctively than is possible with additive or FM synthesis.
A Csound Two-Oscillator Synthesizer
The first example represents perhaps the classic idea of subtractive synthesis: a simple two oscillator synth filtered using a single resonant lowpass filter. Many of the ideas used in this example have been inspired by the design of the Minimoog synthesizer (1970) and other similar instruments.
Each oscillator can describe either a sawtooth, PWM waveform (i.e. square - pulse etc.) or white noise and each oscillator can be transposed in octaves or in cents with respect to a fundamental pitch. The two oscillators are mixed and then passed through a 4-pole / 24dB per octave resonant lowpass filter. The opcode 'moogladder' is chosen on account of its authentic vintage character. The cutoff frequency of the filter is modulated using an ADSR-style (attack-decay-sustain-release) envelope facilitating the creation of dynamic, evolving spectra. Finally the sound output of the filter is shaped by an ADSR amplitude envelope. Waveforms such as sawtooths and square waves offer rich sources for subtractive synthesis as they contain a lot of sound energy across a wide range of frequencies - it could be said that white noise offers the richest sound source containing, as it does, energy at every frequency. A sine wave would offer a very poor source for subtractive synthesis as it contains energy at only one frequency. Other Csound opcodes that might provide rich sources are the buzz and gbuzz opcodes and the GEN09, GEN10, GEN11 and GEN19 GEN routines.
As this instrument is suggestive of a performance instrument controlled via MIDI, this has been partially implemented. Through the use of Csound's MIDI interoperability opcode, mididefault, the instrument can be operated from the score or from a MIDI keyboard. If a MIDI note is received, suitable default p-field values are substituted for the missing p-fields. In the next example MIDI controller 1 will be used to control the global cutoff frequency for the filter.
A schematic for this instrument is shown below:
EXAMPLE 04B01_Subtractive_Midi.csd
<CsoundSynthesizer>
<CsOptions>
-odac -Ma
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 4
nchnls = 2
0dbfs = 1
initc7 1,1,0.8 ;set initial controller position
prealloc 1, 10
instr 1
iNum notnum ;read in midi note number
iCF ctrl7 1,1,0.1,14 ;read in midi controller 1
; set up default p-field values for midi activated notes
mididefault iNum, p4 ;pitch (note number)
mididefault 0.3, p5 ;amplitude 1
mididefault 2, p6 ;type 1
mididefault 0.5, p7 ;pulse width 1
mididefault 0, p8 ;octave disp. 1
mididefault 0, p9 ;tuning disp. 1
mididefault 0.3, p10 ;amplitude 2
mididefault 1, p11 ;type 2
mididefault 0.5, p12 ;pulse width 2
mididefault -1, p13 ;octave displacement 2
mididefault 20, p14 ;tuning disp. 2
mididefault iCF, p15 ;filter cutoff freq
mididefault 0.01, p16 ;filter env. attack time
mididefault 1, p17 ;filter env. decay time
mididefault 0.01, p18 ;filter env. sustain level
mididefault 0.1, p19 ;filter release time
mididefault 0.3, p20 ;filter resonance
mididefault 0.01, p21 ;amp. env. attack
mididefault 0.1, p22 ;amp. env. decay.
mididefault 1, p23 ;amp. env. sustain
mididefault 0.01, p24 ;amp. env. release
; asign p-fields to variables
iCPS = cpsmidinn(p4) ;convert from note number to cps
kAmp1 = p5
iType1 = p6
kPW1 = p7
kOct1 = octave(p8) ;convert from octave displacement to multiplier
kTune1 = cent(p9) ;convert from cents displacement to multiplier
kAmp2 = p10
iType2 = p11
kPW2 = p12
kOct2 = octave(p13)
kTune2 = cent(p14)
iCF = p15
iFAtt = p16
iFDec = p17
iFSus = p18
iFRel = p19
kRes = p20
iAAtt = p21
iADec = p22
iASus = p23
iARel = p24
;oscillator 1
;if type is sawtooth or square...
if iType1==1||iType1==2 then
;...derive vco2 'mode' from waveform type
iMode1 = (iType1=1?0:2)
aSig1 vco2 kAmp1,iCPS*kOct1*kTune1,iMode1,kPW1;VCO audio oscillator
else ;otherwise...
aSig1 noise kAmp1, 0.5 ;...generate white noise
endif
;oscillator 2 (identical in design to oscillator 1)
if iType2==1||iType2==2 then
iMode2 = (iType2=1?0:2)
aSig2 vco2 kAmp2,iCPS*kOct2*kTune2,iMode2,kPW2
else
aSig2 noise kAmp2,0.5
endif
;mix oscillators
aMix sum aSig1,aSig2
;lowpass filter
kFiltEnv expsegr 0.0001,iFAtt,iCPS*iCF,iFDec,iCPS*iCF*iFSus,iFRel,0.0001
aOut moogladder aMix, kFiltEnv, kRes
;amplitude envelope
aAmpEnv expsegr 0.0001,iAAtt,1,iADec,iASus,iARel,0.0001
aOut = aOut*aAmpEnv
outs aOut,aOut
endin
</CsInstruments>
<CsScore>
;p4 = oscillator frequency
;oscillator 1
;p5 = amplitude
;p6 = type (1=sawtooth,2=square-PWM,3=noise)
;p7 = PWM (square wave only)
;p8 = octave displacement
;p9 = tuning displacement (cents)
;oscillator 2
;p10 = amplitude
;p11 = type (1=sawtooth,2=square-PWM,3=noise)
;p12 = pwm (square wave only)
;p13 = octave displacement
;p14 = tuning displacement (cents)
;global filter envelope
;p15 = cutoff
;p16 = attack time
;p17 = decay time
;p18 = sustain level (fraction of cutoff)
;p19 = release time
;p20 = resonance
;global amplitude envelope
;p21 = attack time
;p22 = decay time
;p23 = sustain level
;p24 = release time
; p1 p2 p3 p4 p5 p6 p7 p8 p9 p10 p11 p12 p13
;p14 p15 p16 p17 p18 p19 p20 p21 p22 p23 p24
i 1 0 1 50 0 2 .5 0 -5 0 2 0.5 0 \
5 12 .01 2 .01 .1 0 .005 .01 1 .05
i 1 + 1 50 .2 2 .5 0 -5 .2 2 0.5 0 \
5 1 .01 1 .1 .1 .5 .005 .01 1 .05
i 1 + 1 50 .2 2 .5 0 -8 .2 2 0.5 0 \
8 3 .01 1 .1 .1 .5 .005 .01 1 .05
i 1 + 1 50 .2 2 .5 0 -8 .2 2 0.5 -1 \
8 7 .01 1 .1 .1 .5 .005 .01 1 .05
i 1 + 3 50 .2 1 .5 0 -10 .2 1 0.5 -2 \
10 40 .01 3 .001 .1 .5 .005 .01 1 .05
i 1 + 10 50 1 2 .01 -2 0 .2 3 0.5 0 \
0 40 5 5 .001 1.5 .1 .005 .01 1 .05
f 0 3600
e
</CsScore>
</CsoundSynthesizer>
Simulation of Timbres from a Noise Source
The next example makes extensive use of bandpass filters arranged in parallel to filter white noise. The bandpass filter bandwidths are narrowed to the point where almost pure tones are audible. The crucial difference is that the noise source always induces instability in the amplitude and frequency of tones produced - it is this quality that makes this sort of subtractive synthesis sound much more organic than an additive synthesis equivalent. If the bandwidths are widened, then more of the characteristic of the noise source comes through and the tone becomes 'airier' and less distinct; if the bandwidths are narrowed, the resonating tones become clearer and steadier. By varying the bandwidths interesting metamorphoses of the resultant sound are possible.
22 reson filters are used for the bandpass filters on account of their ability to ring and resonate as their bandwidth narrows. Another reason for this choice is the relative CPU economy of the reson filter, a not insignificant concern as so many of them are used. The frequency ratios between the 22 parallel filters are derived from analysis of a hand bell, the data was found in the appendix of the Csound manual here. Obviously with so much repetition of similar code, some sort of abstraction would be a good idea (perhaps through a UDO or by using a macro), but here, and for the sake of clarity, it is left unabstracted.
In addition to the white noise as a source, noise impulses are also used as a sound source (via the 'mpulse' opcode). The instrument will automatically and randomly slowly crossfade between these two sound sources.
A lowpass and highpass filter are inserted in series before the parallel bandpass filters to shape the frequency spectrum of the source sound. Csound's butterworth filters butlp and buthp are chosen for this task on account of their steep cutoff slopes and minimal ripple at the cutoff frequency.
The outputs of the reson filters are sent alternately to the left and right outputs in order to create a broad stereo effect.
This example makes extensive use of the 'rspline' opcode, a generator of random spline functions, to slowly undulate the many input parameters. The orchestra is self generative in that instrument 1 repeatedly triggers note events in instrument 2 and the extensive use of random functions means that the results will continually evolve as the orchestra is allowed to perform.
A flow diagram for this instrument is shown below:
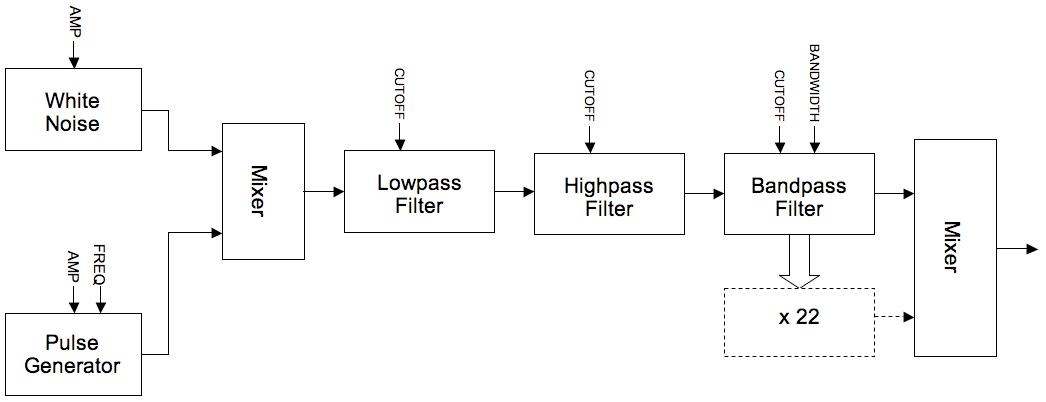
EXAMPLE 04B02_Subtractive_timbres.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example written by Iain McCurdy
sr = 44100
ksmps = 16
nchnls = 2
0dbfs = 1
instr 1 ; triggers notes in instrument 2 with randomised p-fields
krate randomi 0.2,0.4,0.1 ;rate of note generation
ktrig metro krate ;triggers used by schedkwhen
koct random 5,12 ;fundemental pitch of synth note
kdur random 15,30 ;duration of note
schedkwhen ktrig,0,0,2,0,kdur,cpsoct(koct) ;trigger a note in instrument 2
endin
instr 2 ; subtractive synthesis instrument
aNoise pinkish 1 ;a noise source sound: pink noise
kGap rspline 0.3,0.05,0.2,2 ;time gap between impulses
aPulse mpulse 15, kGap ;a train of impulses
kCFade rspline 0,1,0.1,1 ;crossfade point between noise and impulses
aInput ntrpol aPulse,aNoise,kCFade;implement crossfade
; cutoff frequencies for low and highpass filters
kLPF_CF rspline 13,8,0.1,0.4
kHPF_CF rspline 5,10,0.1,0.4
; filter input sound with low and highpass filters in series -
; - done twice per filter in order to sharpen cutoff slopes
aInput butlp aInput, cpsoct(kLPF_CF)
aInput butlp aInput, cpsoct(kLPF_CF)
aInput buthp aInput, cpsoct(kHPF_CF)
aInput buthp aInput, cpsoct(kHPF_CF)
kcf rspline p4*1.05,p4*0.95,0.01,0.1 ; fundemental
; bandwidth for each filter is created individually as a random spline function
kbw1 rspline 0.00001,10,0.2,1
kbw2 rspline 0.00001,10,0.2,1
kbw3 rspline 0.00001,10,0.2,1
kbw4 rspline 0.00001,10,0.2,1
kbw5 rspline 0.00001,10,0.2,1
kbw6 rspline 0.00001,10,0.2,1
kbw7 rspline 0.00001,10,0.2,1
kbw8 rspline 0.00001,10,0.2,1
kbw9 rspline 0.00001,10,0.2,1
kbw10 rspline 0.00001,10,0.2,1
kbw11 rspline 0.00001,10,0.2,1
kbw12 rspline 0.00001,10,0.2,1
kbw13 rspline 0.00001,10,0.2,1
kbw14 rspline 0.00001,10,0.2,1
kbw15 rspline 0.00001,10,0.2,1
kbw16 rspline 0.00001,10,0.2,1
kbw17 rspline 0.00001,10,0.2,1
kbw18 rspline 0.00001,10,0.2,1
kbw19 rspline 0.00001,10,0.2,1
kbw20 rspline 0.00001,10,0.2,1
kbw21 rspline 0.00001,10,0.2,1
kbw22 rspline 0.00001,10,0.2,1
imode = 0 ; amplitude balancing method used by the reson filters
a1 reson aInput, kcf*1, kbw1, imode
a2 reson aInput, kcf*1.0019054878049, kbw2, imode
a3 reson aInput, kcf*1.7936737804878, kbw3, imode
a4 reson aInput, kcf*1.8009908536585, kbw4, imode
a5 reson aInput, kcf*2.5201981707317, kbw5, imode
a6 reson aInput, kcf*2.5224085365854, kbw6, imode
a7 reson aInput, kcf*2.9907012195122, kbw7, imode
a8 reson aInput, kcf*2.9940548780488, kbw8, imode
a9 reson aInput, kcf*3.7855182926829, kbw9, imode
a10 reson aInput, kcf*3.8061737804878, kbw10,imode
a11 reson aInput, kcf*4.5689024390244, kbw11,imode
a12 reson aInput, kcf*4.5754573170732, kbw12,imode
a13 reson aInput, kcf*5.0296493902439, kbw13,imode
a14 reson aInput, kcf*5.0455030487805, kbw14,imode
a15 reson aInput, kcf*6.0759908536585, kbw15,imode
a16 reson aInput, kcf*5.9094512195122, kbw16,imode
a17 reson aInput, kcf*6.4124237804878, kbw17,imode
a18 reson aInput, kcf*6.4430640243902, kbw18,imode
a19 reson aInput, kcf*7.0826219512195, kbw19,imode
a20 reson aInput, kcf*7.0923780487805, kbw20,imode
a21 reson aInput, kcf*7.3188262195122, kbw21,imode
a22 reson aInput, kcf*7.5551829268293, kbw22,imode
; amplitude control for each filter output
kAmp1 rspline 0, 1, 0.3, 1
kAmp2 rspline 0, 1, 0.3, 1
kAmp3 rspline 0, 1, 0.3, 1
kAmp4 rspline 0, 1, 0.3, 1
kAmp5 rspline 0, 1, 0.3, 1
kAmp6 rspline 0, 1, 0.3, 1
kAmp7 rspline 0, 1, 0.3, 1
kAmp8 rspline 0, 1, 0.3, 1
kAmp9 rspline 0, 1, 0.3, 1
kAmp10 rspline 0, 1, 0.3, 1
kAmp11 rspline 0, 1, 0.3, 1
kAmp12 rspline 0, 1, 0.3, 1
kAmp13 rspline 0, 1, 0.3, 1
kAmp14 rspline 0, 1, 0.3, 1
kAmp15 rspline 0, 1, 0.3, 1
kAmp16 rspline 0, 1, 0.3, 1
kAmp17 rspline 0, 1, 0.3, 1
kAmp18 rspline 0, 1, 0.3, 1
kAmp19 rspline 0, 1, 0.3, 1
kAmp20 rspline 0, 1, 0.3, 1
kAmp21 rspline 0, 1, 0.3, 1
kAmp22 rspline 0, 1, 0.3, 1
; left and right channel mixes are created using alternate filter outputs.
; This shall create a stereo effect.
aMixL sum a1*kAmp1,a3*kAmp3,a5*kAmp5,a7*kAmp7,a9*kAmp9,a11*kAmp11,\
a13*kAmp13,a15*kAmp15,a17*kAmp17,a19*kAmp19,a21*kAmp21
aMixR sum a2*kAmp2,a4*kAmp4,a6*kAmp6,a8*kAmp8,a10*kAmp10,a12*kAmp12,\
a14*kAmp14,a16*kAmp16,a18*kAmp18,a20*kAmp20,a22*kAmp22
kEnv linseg 0, p3*0.5, 1,p3*0.5,0,1,0 ; global amplitude envelope
outs (aMixL*kEnv*0.00008), (aMixR*kEnv*0.00008) ; audio sent to outputs
endin
</CsInstruments>
<CsScore>
i 1 0 3600 ; instrument 1 (note generator) plays for 1 hour
e
</CsScore>
</CsoundSynthesizer>
Vowel-Sound Emulation Using Bandpass Filtering
The final example in this section uses precisely tuned bandpass filters, to simulate the sound of the human voice expressing vowel sounds. Spectral resonances in this context are often referred to as 'formants'. Five formants are used to simulate the effect of the human mouth and head as a resonating (and therefore filtering) body. The filter data for simulating the vowel sounds A,E,I,O and U as expressed by a bass, tenor, counter-tenor, alto and soprano voice were found in the appendix of the Csound manual here. Bandwidth and intensity (dB) information is also needed to accurately simulate the various vowel sounds.
reson filters are again used but butbp and others could be equally valid choices.
Data is stored in GEN07 linear break point function tables, as this data is read by k-rate line functions we can interpolate and therefore morph between different vowel sounds during a note.
The source sound for the filters comes from either a pink noise generator or a pulse waveform. The pink noise source could be used if the emulation is to be that of just the breath whereas the pulse waveform provides a decent approximation of the human vocal chords buzzing. This instrument can however morph continuously between these two sources.
A flow diagram for this instrument is shown below:
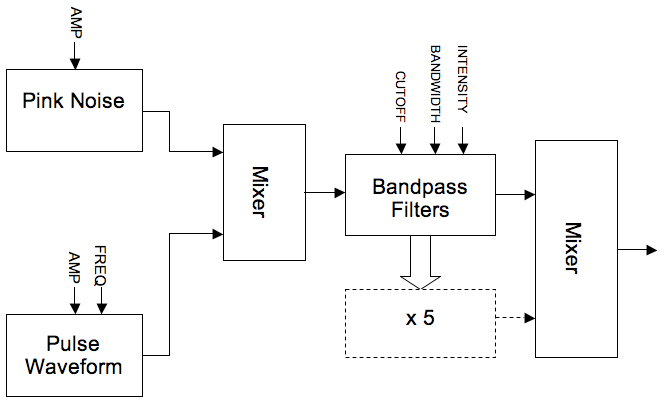
EXAMPLE 04B03_Subtractive_vowels.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;example by Iain McCurdy
sr = 44100
ksmps = 16
nchnls = 2
0dbfs = 1
;FUNCTION TABLES STORING DATA FOR VARIOUS VOICE FORMANTS
;BASS
giBF1 ftgen 0, 0, -5, -2, 600, 400, 250, 400, 350
giBF2 ftgen 0, 0, -5, -2, 1040, 1620, 1750, 750, 600
giBF3 ftgen 0, 0, -5, -2, 2250, 2400, 2600, 2400, 2400
giBF4 ftgen 0, 0, -5, -2, 2450, 2800, 3050, 2600, 2675
giBF5 ftgen 0, 0, -5, -2, 2750, 3100, 3340, 2900, 2950
giBDb1 ftgen 0, 0, -5, -2, 0, 0, 0, 0, 0
giBDb2 ftgen 0, 0, -5, -2, -7, -12, -30, -11, -20
giBDb3 ftgen 0, 0, -5, -2, -9, -9, -16, -21, -32
giBDb4 ftgen 0, 0, -5, -2, -9, -12, -22, -20, -28
giBDb5 ftgen 0, 0, -5, -2, -20, -18, -28, -40, -36
giBBW1 ftgen 0, 0, -5, -2, 60, 40, 60, 40, 40
giBBW2 ftgen 0, 0, -5, -2, 70, 80, 90, 80, 80
giBBW3 ftgen 0, 0, -5, -2, 110, 100, 100, 100, 100
giBBW4 ftgen 0, 0, -5, -2, 120, 120, 120, 120, 120
giBBW5 ftgen 0, 0, -5, -2, 130, 120, 120, 120, 120
;TENOR
giTF1 ftgen 0, 0, -5, -2, 650, 400, 290, 400, 350
giTF2 ftgen 0, 0, -5, -2, 1080, 1700, 1870, 800, 600
giTF3 ftgen 0, 0, -5, -2, 2650, 2600, 2800, 2600, 2700
giTF4 ftgen 0, 0, -5, -2, 2900, 3200, 3250, 2800, 2900
giTF5 ftgen 0, 0, -5, -2, 3250, 3580, 3540, 3000, 3300
giTDb1 ftgen 0, 0, -5, -2, 0, 0, 0, 0, 0
giTDb2 ftgen 0, 0, -5, -2, -6, -14, -15, -10, -20
giTDb3 ftgen 0, 0, -5, -2, -7, -12, -18, -12, -17
giTDb4 ftgen 0, 0, -5, -2, -8, -14, -20, -12, -14
giTDb5 ftgen 0, 0, -5, -2, -22, -20, -30, -26, -26
giTBW1 ftgen 0, 0, -5, -2, 80, 70, 40, 40, 40
giTBW2 ftgen 0, 0, -5, -2, 90, 80, 90, 80, 60
giTBW3 ftgen 0, 0, -5, -2, 120, 100, 100, 100, 100
giTBW4 ftgen 0, 0, -5, -2, 130, 120, 120, 120, 120
giTBW5 ftgen 0, 0, -5, -2, 140, 120, 120, 120, 120
;COUNTER TENOR
giCTF1 ftgen 0, 0, -5, -2, 660, 440, 270, 430, 370
giCTF2 ftgen 0, 0, -5, -2, 1120, 1800, 1850, 820, 630
giCTF3 ftgen 0, 0, -5, -2, 2750, 2700, 2900, 2700, 2750
giCTF4 ftgen 0, 0, -5, -2, 3000, 3000, 3350, 3000, 3000
giCTF5 ftgen 0, 0, -5, -2, 3350, 3300, 3590, 3300, 3400
giTBDb1 ftgen 0, 0, -5, -2, 0, 0, 0, 0, 0
giTBDb2 ftgen 0, 0, -5, -2, -6, -14, -24, -10, -20
giTBDb3 ftgen 0, 0, -5, -2, -23, -18, -24, -26, -23
giTBDb4 ftgen 0, 0, -5, -2, -24, -20, -36, -22, -30
giTBDb5 ftgen 0, 0, -5, -2, -38, -20, -36, -34, -30
giTBW1 ftgen 0, 0, -5, -2, 80, 70, 40, 40, 40
giTBW2 ftgen 0, 0, -5, -2, 90, 80, 90, 80, 60
giTBW3 ftgen 0, 0, -5, -2, 120, 100, 100, 100, 100
giTBW4 ftgen 0, 0, -5, -2, 130, 120, 120, 120, 120
giTBW5 ftgen 0, 0, -5, -2, 140, 120, 120, 120, 120
;ALTO
giAF1 ftgen 0, 0, -5, -2, 800, 400, 350, 450, 325
giAF2 ftgen 0, 0, -5, -2, 1150, 1600, 1700, 800, 700
giAF3 ftgen 0, 0, -5, -2, 2800, 2700, 2700, 2830, 2530
giAF4 ftgen 0, 0, -5, -2, 3500, 3300, 3700, 3500, 2500
giAF5 ftgen 0, 0, -5, -2, 4950, 4950, 4950, 4950, 4950
giADb1 ftgen 0, 0, -5, -2, 0, 0, 0, 0, 0
giADb2 ftgen 0, 0, -5, -2, -4, -24, -20, -9, -12
giADb3 ftgen 0, 0, -5, -2, -20, -30, -30, -16, -30
giADb4 ftgen 0, 0, -5, -2, -36, -35, -36, -28, -40
giADb5 ftgen 0, 0, -5, -2, -60, -60, -60, -55, -64
giABW1 ftgen 0, 0, -5, -2, 50, 60, 50, 70, 50
giABW2 ftgen 0, 0, -5, -2, 60, 80, 100, 80, 60
giABW3 ftgen 0, 0, -5, -2, 170, 120, 120, 100, 170
giABW4 ftgen 0, 0, -5, -2, 180, 150, 150, 130, 180
giABW5 ftgen 0, 0, -5, -2, 200, 200, 200, 135, 200
;SOPRANO
giSF1 ftgen 0, 0, -5, -2, 800, 350, 270, 450, 325
giSF2 ftgen 0, 0, -5, -2, 1150, 2000, 2140, 800, 700
giSF3 ftgen 0, 0, -5, -2, 2900, 2800, 2950, 2830, 2700
giSF4 ftgen 0, 0, -5, -2, 3900, 3600, 3900, 3800, 3800
giSF5 ftgen 0, 0, -5, -2, 4950, 4950, 4950, 4950, 4950
giSDb1 ftgen 0, 0, -5, -2, 0, 0, 0, 0, 0
giSDb2 ftgen 0, 0, -5, -2, -6, -20, -12, -11, -16
giSDb3 ftgen 0, 0, -5, -2, -32, -15, -26, -22, -35
giSDb4 ftgen 0, 0, -5, -2, -20, -40, -26, -22, -40
giSDb5 ftgen 0, 0, -5, -2, -50, -56, -44, -50, -60
giSBW1 ftgen 0, 0, -5, -2, 80, 60, 60, 70, 50
giSBW2 ftgen 0, 0, -5, -2, 90, 90, 90, 80, 60
giSBW3 ftgen 0, 0, -5, -2, 120, 100, 100, 100, 170
giSBW4 ftgen 0, 0, -5, -2, 130, 150, 120, 130, 180
giSBW5 ftgen 0, 0, -5, -2, 140, 200, 120, 135, 200
instr 1
kFund expon p4,p3,p5 ; fundamental
kVow line p6,p3,p7 ; vowel select
kBW line p8,p3,p9 ; bandwidth factor
iVoice = p10 ; voice select
kSrc line p11,p3,p12 ; source mix
aNoise pinkish 3 ; pink noise
aVCO vco2 1.2,kFund,2,0.02 ; pulse tone
aInput ntrpol aVCO,aNoise,kSrc ; input mix
; read formant cutoff frequenies from tables
kCF1 tablei kVow*5,giBF1+(iVoice*15)
kCF2 tablei kVow*5,giBF1+(iVoice*15)+1
kCF3 tablei kVow*5,giBF1+(iVoice*15)+2
kCF4 tablei kVow*5,giBF1+(iVoice*15)+3
kCF5 tablei kVow*5,giBF1+(iVoice*15)+4
; read formant intensity values from tables
kDB1 tablei kVow*5,giBF1+(iVoice*15)+5
kDB2 tablei kVow*5,giBF1+(iVoice*15)+6
kDB3 tablei kVow*5,giBF1+(iVoice*15)+7
kDB4 tablei kVow*5,giBF1+(iVoice*15)+8
kDB5 tablei kVow*5,giBF1+(iVoice*15)+9
; read formant bandwidths from tables
kBW1 tablei kVow*5,giBF1+(iVoice*15)+10
kBW2 tablei kVow*5,giBF1+(iVoice*15)+11
kBW3 tablei kVow*5,giBF1+(iVoice*15)+12
kBW4 tablei kVow*5,giBF1+(iVoice*15)+13
kBW5 tablei kVow*5,giBF1+(iVoice*15)+14
; create resonant formants byt filtering source sound
aForm1 reson aInput, kCF1, kBW1*kBW, 1 ; formant 1
aForm2 reson aInput, kCF2, kBW2*kBW, 1 ; formant 2
aForm3 reson aInput, kCF3, kBW3*kBW, 1 ; formant 3
aForm4 reson aInput, kCF4, kBW4*kBW, 1 ; formant 4
aForm5 reson aInput, kCF5, kBW5*kBW, 1 ; formant 5
; formants are mixed and multiplied both by intensity values derived from tables and by the on-screen gain controls for each formant
aMix sum aForm1*ampdbfs(kDB1),aForm2*ampdbfs(kDB2),aForm3*ampdbfs(kDB3),aForm4*ampdbfs(kDB4),aForm5*ampdbfs(kDB5)
kEnv linseg 0,3,1,p3-6,1,3,0 ; an amplitude envelope
outs aMix*kEnv, aMix*kEnv ; send audio to outputs
endin
</CsInstruments>
<CsScore>
; p4 = fundemental begin value (c.p.s.)
; p5 = fundemental end value
; p6 = vowel begin value (0 - 1 : a e i o u)
; p7 = vowel end value
; p8 = bandwidth factor begin (suggested range 0 - 2)
; p9 = bandwidth factor end
; p10 = voice (0=bass; 1=tenor; 2=counter_tenor; 3=alto; 4=soprano)
; p11 = input source begin (0 - 1 : VCO - noise)
; p12 = input source end
; p4 p5 p6 p7 p8 p9 p10 p11 p12
i 1 0 10 50 100 0 1 2 0 0 0 0
i 1 8 . 78 77 1 0 1 0 1 0 0
i 1 16 . 150 118 0 1 1 0 2 1 1
i 1 24 . 200 220 1 0 0.2 0 3 1 0
i 1 32 . 400 800 0 1 0.2 0 4 0 1
e
</CsScore>
</CsoundSynthesizer>
Conclusion
These examples have hopefully demonstrated the strengths of subtractive synthesis in its simplicity, intuitive operation and its ability to create organic sounding timbres. Further research could explore Csound's other filter opcodes including vcomb, wguide1, wguide2, mode and the more esoteric phaser1, phaser2 and resony.
AMPLITUDE AND RING MODULATION
Introduction
Amplitude-modulation (AM) means, that one oscillator varies the volume/amplitude of an other. If this modulation is done very slowly (1 Hz to 10 Hz) it is recognised as tremolo. Volume-modulation above 10 Hz leads to the effect, that the sound changes its timbre. So called side-bands appear.
EXAMPLE 04C01_Simple_AM.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr = 48000 ksmps = 32 nchnls = 1 0dbfs = 1 instr 1 aRaise expseg 2, 20, 100 aModSine poscil 0.5, aRaise, 1 aDCOffset = 0.5 ; we want amplitude-modulation aCarSine poscil 0.3, 440, 1 out aCarSine*(aModSine + aDCOffset) endin </CsInstruments> <CsScore> f 1 0 1024 10 1 i 1 0 25 e </CsScore> </CsoundSynthesizer> ; written by Alex Hofmann (Mar. 2011)
Theory, Mathematics and Sidebands
The side-bands appear on both sides of the main frequency. This means (freq1-freq2) and (freq1+freq2) appear.
The sounding result of the following example can be calculated as this: freq1 = 440Hz, freq2 = 40 Hz -> The result is a sound with [400, 440, 480] Hz.
The amount of the sidebands can be controlled by a DC-offset of the modulator.
EXAMPLE 04C02_Sidebands.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr = 48000 ksmps = 32 nchnls = 1 0dbfs = 1 instr 1 aOffset linseg 0, 1, 0, 5, 0.6, 3, 0 aSine1 poscil 0.3, 40 , 1 aSine2 poscil 0.3, 440, 1 out (aSine1+aOffset)*aSine2 endin </CsInstruments> <CsScore> f 1 0 1024 10 1 i 1 0 10 e </CsScore> </CsoundSynthesizer> ; written by Alex Hofmann (Mar. 2011)
Ring-modulation is a special-case of AM, without DC-offset (DC-Offset = 0). That means the modulator varies between -1 and +1 like the carrier. The sounding difference to AM is, that RM doesn't contain the carrier frequency.
(If the modulator is unipolar (oscillates between 0 and +1) the effect is called AM.)
More Complex Synthesis using Ring Modulation and Amplitude Modulation
If the modulator itself contains more harmonics, the resulting ring modulated sound becomes more complex.
Carrier freq: 600 Hz
Modulator freqs: 200Hz with 3 harmonics = [200, 400, 600] Hz
Resulting freqs: [0, 200, 400, <-600->, 800, 1000, 1200]
EXAMPLE 04C03_RingMod.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr = 48000 ksmps = 32 nchnls = 1 0dbfs = 1 instr 1 ; Ring-Modulation (no DC-Offset) aSine1 poscil 0.3, 200, 2 ; -> [200, 400, 600] Hz aSine2 poscil 0.3, 600, 1 out aSine1*aSine2 endin </CsInstruments> <CsScore> f 1 0 1024 10 1 ; sine f 2 0 1024 10 1 1 1; 3 harmonics i 1 0 5 e </CsScore> </CsoundSynthesizer> ; written by Alex Hofmann (Mar. 2011)
Using an inharmonic modulator frequency also makes the result sound inharmonic. Varying the DC-offset makes the sound-spectrum evolve over time.
Modulator freqs: [230, 460, 690]
Resulting freqs: [ (-)90, 140, 370, <-600->, 830, 1060, 1290]
(negative frequencies become mirrored, but phase inverted)
EXAMPLE 04C04_Evolving_AM.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr = 48000 ksmps = 32 nchnls = 1 0dbfs = 1 instr 1 ; Amplitude-Modulation aOffset linseg 0, 1, 0, 5, 1, 3, 0 aSine1 poscil 0.3, 230, 2 ; -> [230, 460, 690] Hz aSine2 poscil 0.3, 600, 1 out (aSine1+aOffset)*aSine2 endin </CsInstruments> <CsScore> f 1 0 1024 10 1 ; sine f 2 0 1024 10 1 1 1; 3 harmonics i 1 0 10 e </CsScore> </CsoundSynthesizer>
Csound: FREQUENCYMODULATION
FREQUENCY MODULATION
From Vibrato to the Emergence of Sidebands
A vibrato is a periodical change of pitch, normally less than a halftone and with a slow changing-rate (around 5Hz). Frequency modulation is usually implemented using sine-wave oscillators.
EXAMPLE 04D01_Vibrato.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr = 48000 ksmps = 32 nchnls = 2 0dbfs = 1 instr 1 aMod poscil 10, 5 , 1 ; 5 Hz vibrato with 10 Hz modulation-width aCar poscil 0.3, 440+aMod, 1 ; -> vibrato between 430-450 Hz outs aCar, aCar endin </CsInstruments> <CsScore> f 1 0 1024 10 1 ;Sine wave for table 1 i 1 0 2 </CsScore> </CsoundSynthesizer> ; written by Alex Hofmann (Mar. 2011)
As the depth of modulation is increased, it becomes harder to perceive the base-frequency, but it is still vibrato.
EXAMPLE 04D02_Vibrato_deep.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr = 48000 ksmps = 32 nchnls = 2 0dbfs = 1 instr 1 aMod poscil 90, 5 , 1 ; modulate 90Hz ->vibrato from 350 to 530 hz aCar poscil 0.3, 440+aMod, 1 outs aCar, aCar endin </CsInstruments> <CsScore> f 1 0 1024 10 1 ;Sine wave for table 1 i 1 0 2 </CsScore> </CsoundSynthesizer> ; written by Alex Hofmann (Mar. 2011)
The Simple Modulator->Carrier Pairing
Increasing the modulation-rate leads to a different effect. Frequency-modulation with more than 20Hz is no longer recognized as vibrato. The main-oscillator frequency lays in the middle of the sound and sidebands appear above and below. The number of sidebands is related to the modulation amplitude, later this is controlled by the so called modulation-index.
EXAMPLE 04D03_FM_index.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr = 48000 ksmps = 32 nchnls = 2 0dbfs = 1 instr 1 aRaise linseg 2, 10, 100 ;increase modulation from 2Hz to 100Hz aMod poscil 10, aRaise , 1 aCar poscil 0.3, 440+aMod, 1 outs aCar, aCar endin </CsInstruments> <CsScore> f 1 0 1024 10 1 ;Sine wave for table 1 i 1 0 12 </CsScore> </CsoundSynthesizer> ; written by Alex Hofmann (Mar. 2011)
Hereby the main-oscillator is called carrier and the one changing the carriers frequency is the modulator. The modulation-index:
I = mod-amp/mod-freq.
Making changes to the modulation-index changes the amount of overtones, but not the overall volume. That gives the possibility to produce drastic timbre-changes without the risk of distortion.
When carrier and modulator frequency have integer ratios like 1:1, 2:1, 3:2, 5:4.. the sidebands build a harmonic series, which leads to a sound with clear fundamental pitch.
EXAMPLE 04D04_Harmonic_FM.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr = 48000 ksmps = 32 nchnls = 2 0dbfs = 1 instr 1 kCarFreq = 660 ; 660:440 = 3:2 -> harmonic spectrum kModFreq = 440 kIndex = 15 ; high Index.. try lower values like 1, 2, 3.. kIndexM = 0 kMaxDev = kIndex*kModFreq kMinDev = kIndexM*kModFreq kVarDev = kMaxDev-kMinDev kModAmp = kMinDev+kVarDev aModulator poscil kModAmp, kModFreq, 1 aCarrier poscil 0.3, kCarFreq+aModulator, 1 outs aCarrier, aCarrier endin </CsInstruments> <CsScore> f 1 0 1024 10 1 ;Sine wave for table 1 i 1 0 15 </CsScore> </CsoundSynthesizer> ; written by Alex Hofmann (Mar. 2011)
Otherwise the spectrum of the sound is inharmonic, which makes it metallic or noisy. Raising the modulation-index shifts the energy into the side-bands. The side-bands distance is:
Distance in Hz = (carrierFreq)-(k*modFreq) | k = {1, 2, 3, 4 ..}
This calculation can result in negative frequencies. Those become reflected at zero, but with inverted phase! So negative frequencies can erase existing ones. Frequencies over Nyquist-frequency (half of samplingrate) "fold over" (aliasing).
The John Chowning FM Model of a Trumpet
Composer and researcher Jown Chowning worked on the first digital implementation of FM in the 1970's.
Using envelopes to control the modulation index and the overall amplitude gives you the possibility to create evolving sounds with enormous spectral variations. Chowning showed these possibilities in his pieces, where he let the sounds transform. In the piece Sabelithe a drum sound morphes over the time into a trumpet tone.
EXAMPLE 04D05_Trumpet_FM.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr = 48000 ksmps = 32 nchnls = 2 0dbfs = 1 instr 1 ; simple way to generate a trumpet-like sound kCarFreq = 440 kModFreq = 440 kIndex = 5 kIndexM = 0 kMaxDev = kIndex*kModFreq kMinDev = kIndexM * kModFreq kVarDev = kMaxDev-kMinDev aEnv expseg .001, 0.2, 1, p3-0.3, 1, 0.2, 0.001 aModAmp = kMinDev+kVarDev*aEnv aModulator poscil aModAmp, kModFreq, 1 aCarrier poscil 0.3*aEnv, kCarFreq+aModulator, 1 outs aCarrier, aCarrier endin </CsInstruments> <CsScore> f 1 0 1024 10 1 ;Sine wave for table 1 i 1 0 2 </CsScore> </CsoundSynthesizer> ; written by Alex Hofmann (Mar. 2011)
The following example uses the same instrument, with different settings to generate a bell-like sound:
EXAMPLE 04D06_Bell_FM.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr = 48000 ksmps = 32 nchnls = 2 0dbfs = 1 instr 1 ; bell-like sound kCarFreq = 200 ; 200/280 = 5:7 -> inharmonic spectrum kModFreq = 280 kIndex = 12 kIndexM = 0 kMaxDev = kIndex*kModFreq kMinDev = kIndexM * kModFreq kVarDev = kMaxDev-kMinDev aEnv expseg .001, 0.001, 1, 0.3, 0.5, 8.5, .001 aModAmp = kMinDev+kVarDev*aEnv aModulator poscil aModAmp, kModFreq, 1 aCarrier poscil 0.3*aEnv, kCarFreq+aModulator, 1 outs aCarrier, aCarrier endin </CsInstruments> <CsScore> f 1 0 1024 10 1 ;Sine wave for table 1 i 1 0 9 </CsScore> </CsoundSynthesizer> ; written by Alex Hofmann (Mar. 2011)
More Complex FM Algorithms
Combining more than two oscillators (operators) is called complex FM synthesis. Operators can be connected in different combinations; often 4-6 operators are used. The carrier is always the last operator in the row. Changing it's pitch shifts the whole sound. All other operators are modulators, changing their pitch alters the sound-spectrum.
Two into One: M1+M2 -> C
The principle here is, that (M1:C) and (M2:C) will be separate modulations and later added together.
EXAMPLE 04D07_Added_FM.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr = 48000 ksmps = 32 nchnls = 2 0dbfs = 1 instr 1 aMod1 poscil 200, 700, 1 aMod2 poscil 1800, 290, 1 aSig poscil 0.3, 440+aMod1+aMod2, 1 outs aSig, aSig endin </CsInstruments> <CsScore> f 1 0 1024 10 1 ;Sine wave for table 1 i 1 0 3 </CsScore> </CsoundSynthesizer> ; written by Alex Hofmann (Mar. 2011)
In series: M1->M2->C
This is much more complicated to calculate and sound-timbre becomes harder to predict, because M1:M2 produces a complex spectrum (W), which then modulates the carrier (W:C).
EXAMPLE 04D08_Serial_FM.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr = 48000 ksmps = 32 nchnls = 2 0dbfs = 1 instr 1 aMod1 poscil 200, 700, 1 aMod2 poscil 1800, 290+aMod1, 1 aSig poscil 0.3, 440+aMod2, 1 outs aSig, aSig endin </CsInstruments> <CsScore> f 1 0 1024 10 1 ;Sine wave for table 1 i 1 0 3 </CsScore> </CsoundSynthesizer> ; written by Alex Hofmann (Mar. 2011)
Phase Modulation - the Yamaha DX7 and Feedback FM
There is a strong relation between frequency modulation and phase modulation, as both techniques influence the oscillator's pitch, and the resulting timbre modifications are the same.
If you'd like to build a feedbacking FM system, it will happen that the self-modulation comes to a zero point, which stops the oscillator forever. To avoid this, it is more practical to modulate the carriers table-lookup phase, instead of its pitch.
Even the most famous FM-synthesizer Yamaha DX7 is based on the phase-modulation (PM) technique, because this allows feedback. The DX7 provides 7 operators, and offers 32 routing combinations of these. (http://yala.freeservers.com/t2synths.htm#DX7)
To build a PM-synth in Csound tablei opcode needs to be used as oscillator. In order to step through the f-table, a phasor will output the necessary steps.
EXAMPLE 04D09_PhaseMod.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr = 48000 ksmps = 32 nchnls = 2 0dbfs = 1 instr 1 ; simple PM-Synth kCarFreq = 200 kModFreq = 280 kModFactor = kCarFreq/kModFreq kIndex = 12/6.28 ; 12/2pi to convert from radians to norm. table index aEnv expseg .001, 0.001, 1, 0.3, 0.5, 8.5, .001 aModulator poscil kIndex*aEnv, kModFreq, 1 aPhase phasor kCarFreq aCarrier tablei aPhase+aModulator, 1, 1, 0, 1 outs (aCarrier*aEnv), (aCarrier*aEnv) endin </CsInstruments> <CsScore> f 1 0 1024 10 1 ;Sine wave for table 1 i 1 0 9 </CsScore> </CsoundSynthesizer> ; written by Alex Hofmann (Mar. 2011)
Let's use the possibilities of self-modulation (feedback-modulation) of the oscillator. So in the following example, the oscillator is both modulator and carrier. To control the amount of modulation, an envelope scales the feedback.
EXAMPLE 04D10_Feedback_modulation.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr = 48000 ksmps = 32 nchnls = 2 0dbfs = 1 instr 1 ; feedback PM kCarFreq = 200 kFeedbackAmountEnv linseg 0, 2, 0.2, 0.1, 0.3, 0.8, 0.2, 1.5, 0 aAmpEnv expseg .001, 0.001, 1, 0.3, 0.5, 8.5, .001 aPhase phasor kCarFreq aCarrier init 0 ; init for feedback aCarrier tablei aPhase+(aCarrier*kFeedbackAmountEnv), 1, 1, 0, 1 outs aCarrier*aAmpEnv, aCarrier*aAmpEnv endin </CsInstruments> <CsScore> f 1 0 1024 10 1 ;Sine wave for table 1 i 1 0 9 </CsScore> </CsoundSynthesizer> ; written by Alex Hofmann (Mar. 2011)
Csound: WAVESHAPING
WAVESHAPING
Waveshaping is in some ways a relation of modulation techniques such as frequency or phase modulation. Waveshaping can create quite dramatic sound transformations through the application of a very simple process. In FM (frequency modulation) modulation synthesis occurs between two oscillators, waveshaping is implemented using a single oscillator (usually a simple sine oscillator) and a so-called 'transfer function'. The transfer function transforms and shapes the incoming amplitude values using a simple look-up process: if the incoming value is x, the outgoing value becomes y. This can be written as a table with two columns. Here is a simple example:
| Incoming (x) Value | Outgoing (y) Value |
| -0.5 or lower | -1 |
| between -0.5 and 0.5 | remain unchanged |
| 0.5 or higher | 1 |
Illustrating this in an x/y coordinate system results in the following graph:
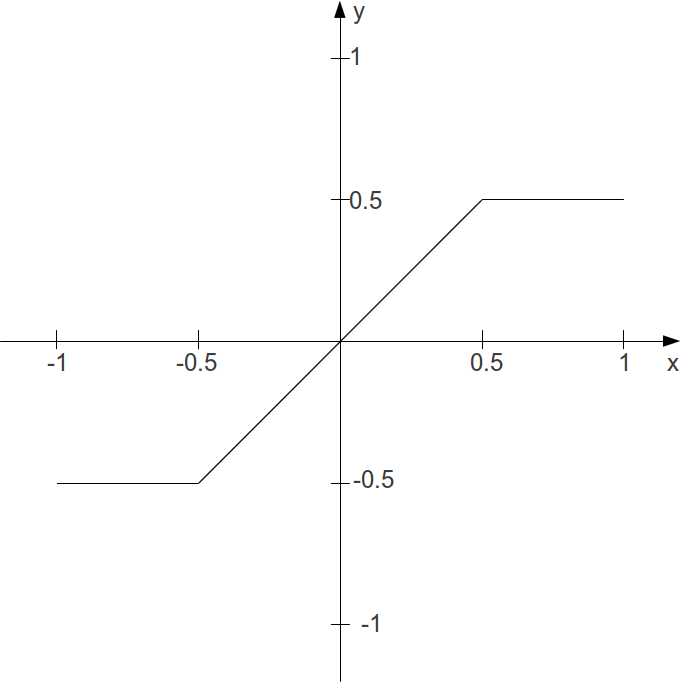
Basic Implementation Model
Although Csound contains several opcodes for waveshaping, implementing waveshaping from first principles as Csound code is fairly straightforward. The x-axis is the amplitude of every single sample, which is in the range of -1 to +1. This number has to be used as index to a table which stores the transfer function. To create a table like the one above, you can use Csound's sub-routine GEN07. This statement will create a table of 4096 points with the desired shape:
giTrnsFnc ftgen 0, 0, 4096, -7, -0.5, 1024, -0.5, 2048, 0.5, 1024, 0.5

Now two problems must be solved. First, the index of the function table is not -1 to +1. Rather, it is either 0 to 4095 in the raw index mode, or 0 to 1 in the normalized mode. The simplest solution is to use the normalized index and scale the incoming amplitudes, so that an amplitude of -1 becomes an index of 0, and an amplitude of 1 becomes an index of 1:
aIndx = (aAmp + 1) / 2
The other problem stems from the difference in the accuracy of possible values in a sample and in a function table. Every single sample is encoded in a 32-bit floating point number in standard audio applications - or even in a 64-bit float in recent Csound. A table with 4096 points results in a 12-bit number, so you will have a serious loss of accuracy (= sound quality) if you use the table values directly. Here, the solution is to use an interpolating table reader. The opcode tablei (instead of table) does this job. This opcode then needs an extra point in the table for interpolating, so we give 4097 as the table size instead of 4096.
This is the code for simple waveshaping using our transfer function which has been discussed previously:
EXAMPLE 04E01_Simple_waveshaping.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giTrnsFnc ftgen 0, 0, 4097, -7, -0.5, 1024, -0.5, 2048, 0.5, 1024, 0.5
giSine ftgen 0, 0, 1024, 10, 1
instr 1
aAmp poscil 1, 400, giSine
aIndx = (aAmp + 1) / 2
aWavShp tablei aIndx, giTrnsFnc, 1
outs aWavShp, aWavShp
endin
</CsInstruments>
<CsScore>
i 1 0 10
</CsScore>
</CsoundSynthesizer>

Powershape
The powershape opcode performs waveshaping by simply raising all samples to the power of a user given exponent. Its main innovation is that the polarity of samples within the negative domain will be retained. It simply performs the power function on absolute values (negative values made positive) and then reinstates the minus sign if required. It also normalises the input signal between -1 and 1 before shaping and then rescales the output by the inverse of whatever multiple was required to normalise the input. This ensures useful results but does require that the user states the maximum amplitude value expected in the opcode declaration and thereafter abide by that limit. The exponent, which the opcode refers to as 'shape amount', can be varied at k-rate thereby facilitating the creation of dynamic spectra upon a constant spectrum input.
If we consider the simplest possible input - a sine wave - a shape amount of '1' will produce no change (raising any value to the power of 1 leaves that value unchanged).
A shaping amount of 2.5 will visibly 'squeeze' the waveform as values less than 1 become increasingly biased towards the zero axis.
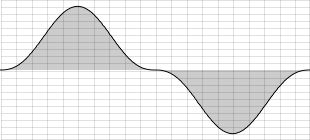
Much higher values will narrow the positive and negative peaks further. Below is the waveform resulting from a shaping amount of 50.
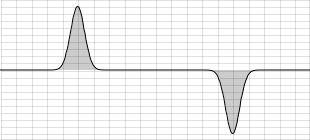
Shape amounts less than 1 (but greater than zero) will give the opposite effect of drawing values closer to -1 or 1. The waveform resulting from a shaping amount of 0.5 shown below is noticeably more rounded than the sine wave input.
Reducing shape amount even closer to zero will start to show squaring of the waveform. The result of a shape amount of 0.1 is shown below.
The sonograms of the five examples shown above are as shown below:
As power (shape amount) is increased from 1 through 2.5 to 50, it can be observed how harmonic partials are added. It is worth noting also that when the power exponent is 50 the strength of the fundamental has waned somewhat. What is not clear from the sonogram is that the partials present are only the odd numbered ones. As the power exponent is reduced below 1 through 0.5 and finally 0.1, odd numbered harmonic partials again appear but this time the strength of the fundamental remains constant. It can also be observed that aliasing is becoming a problem as evidenced by the vertical artifacts in the sonograms for 0.5 and in particular 0.1. This is a significant concern when using waveshaping techniques. Raising the sampling rate can provide additional headroom before aliasing manifests but ultimately subtlety in waveshaping's use is paramount.
Distort
The distort opcode, authored by Csound's original creator Barry Vercoe, was originally part of the Extended Csound project but was introduced into Canonical Csound in version 5. It waveshapes an input signal according to a transfer function provided by the user using a function table. At first glance this may seem to offer little more than what we have already demonstrated from first principles, but it offers a number of additional features that enhance its usability. The input signal first has soft-knee compression applied before being mapped through the transfer function. Input gain is also provided via the 'distortion amount' input argument and this provides dynamic control of the waveshaping transformation. The result of using compression means that spectrally the results are better behaved than is typical with waveshaping. A common transfer function would be the hyperbolic tangent (tanh) function. Csound now possesses an GEN routine GENtanh for the creation of tanh functions:
GENtanh f # time size "tanh" start end rescale
By adjusting the 'start' and 'end' values we can modify the shape of the tanh transfer function and therefore the aggressiveness of the waveshaping ('start' and 'end' values should be the same absolute values and negative and positive respectively if we want the function to pass through the origin from the lower left quadrant to the upper right quadrant).
Start and end values of -1 and 1 will produce a gentle 's' curve.

This represents only a very slight deviation from a straight line function from (-1,-1) to (1,1) - which would produce no distortion - therefore the effects of the above used as a transfer function will be extremely subtle.
Start and end points of -5 and 5 will produce a much more dramatic curve and more dramatic waveshaping:
f 1 0 1024 "tanh" -5 5 0
Note that the GEN routine's argument p7 for rescaling is set to zero ensuring that the function only ever extends from -1 and 1. The values provided for 'start' and 'end' only alter the shape.
In the following test example a sine wave at 200 hz is waveshaped using distort and the tanh function shown above.
EXAMPLE 04E02_Distort_1.csd
<CsoundSynthesizer> <CsOptions> -dm0 -odac </CsOptions> <CsInstruments> sr = 44100 ksmps =32 nchnls = 1 0dbfs = 1 giSine ftgen 1,0,1025,10,1 ; sine function giTanh ftgen 2,0,257,"tanh",-10,10,0 ; tanh function instr 1 aSig poscil 1, 200, giSine ; a sine wave kAmt line 0, p3, 1 ; rising distortion amount aDst distort aSig, kAmt, giTanh ; distort the sine tone out aDst*0.1 endin </CsInstruments> <CsScore> i 1 0 4 </CsScore> </CsoundSynthesizer>
The resulting sonogram looks like this:

As the distort amount is raised from zero to 1 it can be seen from the sonogram how upper partials emerge and gain in strength. Only the odd numbered partials are produced, therefore over the fundemental at 200 hz partials are present at 600, 1000, 1400 hz and so on. If we want to restore the even numbered partials we can simultaneously waveshape a sine at 400 hz, one octave above the fundamental as in the next example:
EXAMPLE 04E03_Distort_2.csd
<CsoundSynthesizer> <CsOptions> -dm0 -odac </CsOptions> <CsInstruments> sr = 44100 ksmps =32 nchnls = 1 0dbfs = 1 giSine ftgen 1,0,1025,10,1 giTanh ftgen 2,0,257,"tanh",-10,10,0 instr 1 kAmt line 0, p3, 1 ; rising distortion amount aSig poscil 1, 200, giSine ; a sine aSig2 poscil kAmt*0.8,400,giSine ; a sine an octave above aDst distort aSig+aSig2, kAmt, giTanh ; distort a mixture of the two sines out aDst*0.1 endin </CsInstruments> <CsScore> i 1 0 4 </CsScore> </CsoundSynthesizer>
The higher of the two sines is faded in using the distortion amount control so that when distortion amount if zero we will be left with only the fundamental. The sonogram looks like this:
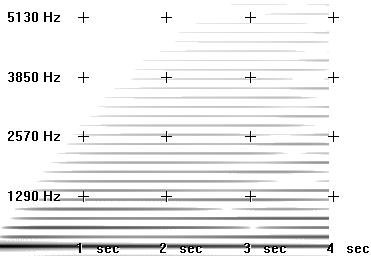
What we hear this time is something close to a sawtooth waveform with a rising low-pass filter. The higher of the two input sines at 400 hz will produce overtones at 1200, 2000, 2800... thereby filling in the missing partials.
REFERENCES
Distortion Synthesis - a tutorial with Csound examples by Victor Lazzarini http://www.csounds.com/journal/issue11/distortionSynthesis.html
Csound: GRANULARSYNTHESIS
GRANULAR SYNTHESIS
Concept Behind Granular Synthesis
Granular synthesis is a technique in which a source sound or waveform is broken into many fragments, often of very short duration, which are then restructured and rearranged according to various patterning and indeterminacy functions.
If we imagine the simplest possible granular synthesis algorithm in which a precise fragment of sound is repeated with regularity, there are two principle attributes of this process that we are most concerned with. Firstly the duration of each sound grain is significant: if the grain duration if very small, typically less than 0.02 seconds, then less of the characteristics of the source sound will be evident. If the grain duration is greater than 0.02 then more of the character of the source sound or waveform will be evident. Secondly the rate at which grains are generated will be significant: if grain generation is below 20 hertz, i.e. less than 20 grains per second, then the stream of grains will be perceived as a rhythmic pulsation; if rate of grain generation increases beyond 20 Hz then individual grains will be harder to distinguish and instead we will begin to perceive a buzzing tone, the fundamental of which will correspond to the frequency of grain generation. Any pitch contained within the source material is not normally perceived as the fundamental of the tone whenever grain generation is periodic, instead the pitch of the source material or waveform will be perceived as a resonance peak (sometimes referred to as a formant); therefore transposition of the source material will result in the shifting of this resonance peak.
Granular Synthesis Demonstrated Using First Principles
The following example exemplifies the concepts discussed above. None of Csound's built-in granular synthesis opcodes are used, instead schedkwhen in instrument 1 is used to precisely control the triggering of grains in instrument 2. Three notes in instrument 1 are called from the score one after the other which in turn generate three streams of grains in instrument 2. The first note demonstrates the transition from pulsation to the perception of a tone as the rate of grain generation extends beyond 20 Hz. The second note demonstrates the loss of influence of the source material as the grain duration is reduced below 0.02 seconds. The third note demonstrates how shifting the pitch of the source material for the grains results in the shifting of a resonance peak in the output tone. In each case information regarding rate of grain generation, duration and fundamental (source material pitch) is output to the terminal every 1/2 second so that the user can observe the changing parameters.
It should also be noted how the amplitude of each grain is enveloped in instrument 2. If grains were left unenveloped they would likely produce clicks on account of discontinuities in the waveform produced at the beginning and ending of each grain.
Granular synthesis in which grain generation occurs with perceivable periodicity is referred to as synchronous granular synthesis. Granular synthesis in which this periodicity is not evident is referred to as asynchronous granular synthesis.
EXAMPLE 04F01_GranSynth_basic.csd
<CsoundSynthesizer>
<CsOptions>
-odac -m0
</CsOptions>
<CsInstruments>
;Example by Iain McCurdy
sr = 44100
ksmps = 1
nchnls = 1
0dbfs = 1
giSine ftgen 0,0,4096,10,1
instr 1
kRate expon p4,p3,p5 ; rate of grain generation
kTrig metro kRate ; a trigger to generate grains
kDur expon p6,p3,p7 ; grain duration
kForm expon p8,p3,p9 ; formant (spectral centroid)
; p1 p2 p3 p4
schedkwhen kTrig,0,0,2, 0, kDur,kForm ;trigger a note(grain) in instr 2
;print data to terminal every 1/2 second
printks "Rate:%5.2F Dur:%5.2F Formant:%5.2F%n", 0.5, kRate , kDur, kForm
endin
instr 2
iForm = p4
aEnv linseg 0,0.005,0.2,p3-0.01,0.2,0.005,0
aSig poscil aEnv, iForm, giSine
out aSig
endin
</CsInstruments>
<CsScore>
;p4 = rate begin
;p5 = rate end
;p6 = duration begin
;p7 = duration end
;p8 = formant begin
;p9 = formant end
; p1 p2 p3 p4 p5 p6 p7 p8 p9
i 1 0 30 1 100 0.02 0.02 400 400 ;demo of grain generation rate
i 1 31 10 10 10 0.4 0.01 400 400 ;demo of grain size
i 1 42 20 50 50 0.02 0.02 100 5000 ;demo of changing formant
e
</CsScore>
</CsoundSynthesizer>
Granular Synthesis of Vowels: FOF
The principles outlined in the previous example can be extended to imitate vowel sounds produced by the human voice. This type of granular synthesis is referred to as FOF (fonction d'onde formatique) synthesis and is based on work by Xavier Rodet on his CHANT program at IRCAM. Typically five synchronous granular synthesis streams will be used to create five different resonant peaks in a fundamental tone in order to imitate different vowel sounds expressible by the human voice. The most crucial element in defining a vowel imitation is the degree to which the source material within each of the five grain streams is transposed. Bandwidth (essentially grain duration) and intensity (loudness) of each grain stream are also important indicators in defining the resultant sound.
Csound has a number of opcodes that make working with FOF synthesis easier. We will be using fof.
Information regarding frequency, bandwidth and intensity values that will produce various vowel sounds for different voice types can be found in the appendix of the Csound manual here. These values are stored in function tables in the FOF synthesis example. GEN07, which produces linear break point envelopes, is chosen as we will then be able to morph continuously between vowels.
EXAMPLE 04F02_Fof_vowels.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;example by Iain McCurdy
sr = 44100
ksmps = 16
nchnls = 2
0dbfs = 1
;FUNCTION TABLES STORING DATA FOR VARIOUS VOICE FORMANTS
;BASS
giBF1 ftgen 0, 0, -5, -2, 600, 400, 250, 400, 350
giBF2 ftgen 0, 0, -5, -2, 1040, 1620, 1750, 750, 600
giBF3 ftgen 0, 0, -5, -2, 2250, 2400, 2600, 2400, 2400
giBF4 ftgen 0, 0, -5, -2, 2450, 2800, 3050, 2600, 2675
giBF5 ftgen 0, 0, -5, -2, 2750, 3100, 3340, 2900, 2950
giBDb1 ftgen 0, 0, -5, -2, 0, 0, 0, 0, 0
giBDb2 ftgen 0, 0, -5, -2, -7, -12, -30, -11, -20
giBDb3 ftgen 0, 0, -5, -2, -9, -9, -16, -21, -32
giBDb4 ftgen 0, 0, -5, -2, -9, -12, -22, -20, -28
giBDb5 ftgen 0, 0, -5, -2, -20, -18, -28, -40, -36
giBBW1 ftgen 0, 0, -5, -2, 60, 40, 60, 40, 40
giBBW2 ftgen 0, 0, -5, -2, 70, 80, 90, 80, 80
giBBW3 ftgen 0, 0, -5, -2, 110, 100, 100, 100, 100
giBBW4 ftgen 0, 0, -5, -2, 120, 120, 120, 120, 120
giBBW5 ftgen 0, 0, -5, -2, 130, 120, 120, 120, 120
;TENOR
giTF1 ftgen 0, 0, -5, -2, 650, 400, 290, 400, 350
giTF2 ftgen 0, 0, -5, -2, 1080, 1700, 1870, 800, 600
giTF3 ftgen 0, 0, -5, -2, 2650, 2600, 2800, 2600, 2700
giTF4 ftgen 0, 0, -5, -2, 2900, 3200, 3250, 2800, 2900
giTF5 ftgen 0, 0, -5, -2, 3250, 3580, 3540, 3000, 3300
giTDb1 ftgen 0, 0, -5, -2, 0, 0, 0, 0, 0
giTDb2 ftgen 0, 0, -5, -2, -6, -14, -15, -10, -20
giTDb3 ftgen 0, 0, -5, -2, -7, -12, -18, -12, -17
giTDb4 ftgen 0, 0, -5, -2, -8, -14, -20, -12, -14
giTDb5 ftgen 0, 0, -5, -2, -22, -20, -30, -26, -26
giTBW1 ftgen 0, 0, -5, -2, 80, 70, 40, 40, 40
giTBW2 ftgen 0, 0, -5, -2, 90, 80, 90, 80, 60
giTBW3 ftgen 0, 0, -5, -2, 120, 100, 100, 100, 100
giTBW4 ftgen 0, 0, -5, -2, 130, 120, 120, 120, 120
giTBW5 ftgen 0, 0, -5, -2, 140, 120, 120, 120, 120
;COUNTER TENOR
giCTF1 ftgen 0, 0, -5, -2, 660, 440, 270, 430, 370
giCTF2 ftgen 0, 0, -5, -2, 1120, 1800, 1850, 820, 630
giCTF3 ftgen 0, 0, -5, -2, 2750, 2700, 2900, 2700, 2750
giCTF4 ftgen 0, 0, -5, -2, 3000, 3000, 3350, 3000, 3000
giCTF5 ftgen 0, 0, -5, -2, 3350, 3300, 3590, 3300, 3400
giTBDb1 ftgen 0, 0, -5, -2, 0, 0, 0, 0, 0
giTBDb2 ftgen 0, 0, -5, -2, -6, -14, -24, -10, -20
giTBDb3 ftgen 0, 0, -5, -2, -23, -18, -24, -26, -23
giTBDb4 ftgen 0, 0, -5, -2, -24, -20, -36, -22, -30
giTBDb5 ftgen 0, 0, -5, -2, -38, -20, -36, -34, -30
giTBW1 ftgen 0, 0, -5, -2, 80, 70, 40, 40, 40
giTBW2 ftgen 0, 0, -5, -2, 90, 80, 90, 80, 60
giTBW3 ftgen 0, 0, -5, -2, 120, 100, 100, 100, 100
giTBW4 ftgen 0, 0, -5, -2, 130, 120, 120, 120, 120
giTBW5 ftgen 0, 0, -5, -2, 140, 120, 120, 120, 120
;ALTO
giAF1 ftgen 0, 0, -5, -2, 800, 400, 350, 450, 325
giAF2 ftgen 0, 0, -5, -2, 1150, 1600, 1700, 800, 700
giAF3 ftgen 0, 0, -5, -2, 2800, 2700, 2700, 2830, 2530
giAF4 ftgen 0, 0, -5, -2, 3500, 3300, 3700, 3500, 2500
giAF5 ftgen 0, 0, -5, -2, 4950, 4950, 4950, 4950, 4950
giADb1 ftgen 0, 0, -5, -2, 0, 0, 0, 0, 0
giADb2 ftgen 0, 0, -5, -2, -4, -24, -20, -9, -12
giADb3 ftgen 0, 0, -5, -2, -20, -30, -30, -16, -30
giADb4 ftgen 0, 0, -5, -2, -36, -35, -36, -28, -40
giADb5 ftgen 0, 0, -5, -2, -60, -60, -60, -55, -64
giABW1 ftgen 0, 0, -5, -2, 50, 60, 50, 70, 50
giABW2 ftgen 0, 0, -5, -2, 60, 80, 100, 80, 60
giABW3 ftgen 0, 0, -5, -2, 170, 120, 120, 100, 170
giABW4 ftgen 0, 0, -5, -2, 180, 150, 150, 130, 180
giABW5 ftgen 0, 0, -5, -2, 200, 200, 200, 135, 200
;SOPRANO
giSF1 ftgen 0, 0, -5, -2, 800, 350, 270, 450, 325
giSF2 ftgen 0, 0, -5, -2, 1150, 2000, 2140, 800, 700
giSF3 ftgen 0, 0, -5, -2, 2900, 2800, 2950, 2830, 2700
giSF4 ftgen 0, 0, -5, -2, 3900, 3600, 3900, 3800, 3800
giSF5 ftgen 0, 0, -5, -2, 4950, 4950, 4950, 4950, 4950
giSDb1 ftgen 0, 0, -5, -2, 0, 0, 0, 0, 0
giSDb2 ftgen 0, 0, -5, -2, -6, -20, -12, -11, -16
giSDb3 ftgen 0, 0, -5, -2, -32, -15, -26, -22, -35
giSDb4 ftgen 0, 0, -5, -2, -20, -40, -26, -22, -40
giSDb5 ftgen 0, 0, -5, -2, -50, -56, -44, -50, -60
giSBW1 ftgen 0, 0, -5, -2, 80, 60, 60, 70, 50
giSBW2 ftgen 0, 0, -5, -2, 90, 90, 90, 80, 60
giSBW3 ftgen 0, 0, -5, -2, 120, 100, 100, 100, 170
giSBW4 ftgen 0, 0, -5, -2, 130, 150, 120, 130, 180
giSBW5 ftgen 0, 0, -5, -2, 140, 200, 120, 135, 200
gisine ftgen 0, 0, 4096, 10, 1
giexp ftgen 0, 0, 1024, 19, 0.5, 0.5, 270, 0.5
instr 1
kFund expon p4,p3,p5 ; fundemental
kVow line p6,p3,p7 ; vowel select
kBW line p8,p3,p9 ; bandwidth factor
iVoice = p10 ; voice select
; read formant cutoff frequenies from tables
kForm1 tablei kVow*5,giBF1+(iVoice*15)
kForm2 tablei kVow*5,giBF1+(iVoice*15)+1
kForm3 tablei kVow*5,giBF1+(iVoice*15)+2
kForm4 tablei kVow*5,giBF1+(iVoice*15)+3
kForm5 tablei kVow*5,giBF1+(iVoice*15)+4
; read formant intensity values from tables
kDB1 tablei kVow*5,giBF1+(iVoice*15)+5
kDB2 tablei kVow*5,giBF1+(iVoice*15)+6
kDB3 tablei kVow*5,giBF1+(iVoice*15)+7
kDB4 tablei kVow*5,giBF1+(iVoice*15)+8
kDB5 tablei kVow*5,giBF1+(iVoice*15)+9
; read formant bandwidths from tables
kBW1 tablei kVow*5,giBF1+(iVoice*15)+10
kBW2 tablei kVow*5,giBF1+(iVoice*15)+11
kBW3 tablei kVow*5,giBF1+(iVoice*15)+12
kBW4 tablei kVow*5,giBF1+(iVoice*15)+13
kBW5 tablei kVow*5,giBF1+(iVoice*15)+14
; create resonant formants using fof opcode
koct = 1
aForm1 fof ampdb(kDB1),kFund,kForm1,0,kBW1,0.003,0.02,0.007,\
1000,gisine,giexp,3600
aForm2 fof ampdb(kDB2),kFund,kForm2,0,kBW2,0.003,0.02,0.007,\
1000,gisine,giexp,3600
aForm3 fof ampdb(kDB3),kFund,kForm3,0,kBW3,0.003,0.02,0.007,\
1000,gisine,giexp,3600
aForm4 fof ampdb(kDB4),kFund,kForm4,0,kBW4,0.003,0.02,0.007,\
1000,gisine,giexp,3600
aForm5 fof ampdb(kDB5),kFund,kForm5,0,kBW5,0.003,0.02,0.007,\
1000,gisine,giexp,3600
; formants are mixed
aMix sum aForm1,aForm2,aForm3,aForm4,aForm5
kEnv linseg 0,3,1,p3-6,1,3,0 ; an amplitude envelope
outs aMix*kEnv*0.3, aMix*kEnv*0.3 ; send audio to outputs
endin
</CsInstruments>
<CsScore>
; p4 = fundamental begin value (c.p.s.)
; p5 = fundamental end value
; p6 = vowel begin value (0 - 1 : a e i o u)
; p7 = vowel end value
; p8 = bandwidth factor begin (suggested range 0 - 2)
; p9 = bandwidth factor end
; p10 = voice (0=bass; 1=tenor; 2=counter_tenor; 3=alto; 4=soprano)
; p1 p2 p3 p4 p5 p6 p7 p8 p9 p10
i 1 0 10 50 100 0 1 2 0 0
i 1 8 . 78 77 1 0 1 0 1
i 1 16 . 150 118 0 1 1 0 2
i 1 24 . 200 220 1 0 0.2 0 3
i 1 32 . 400 800 0 1 0.2 0 4
e
</CsScore>
</CsoundSynthesizer>
Asynchronous Granular Synthesis
The previous two examples have played psychoacoustic phenomena associated with the perception of granular textures that exhibit periodicity and patterns. If we introduce indeterminacy into some of the parameters of granular synthesis we begin to lose the coherence of some of these harmonic structures.
The next example is based on the design of example 04F01.csd. Two streams of grains are generated. The first stream begins as a synchronous stream but as the note progresses the periodicity of grain generation is eroded through the addition of an increasing degree of gaussian noise. It will be heard how the tone metamorphosizes from one characterized by steady purity to one of fuzzy airiness. The second the applies a similar process of increasing indeterminacy to the formant parameter (frequency of material within each grain).
Other parameters of granular synthesis such as the amplitude of each grain, grain duration, spatial location etc. can be similarly modulated with random functions to offset the psychoacoustic effects of synchronicity when using constant values.
EXAMPLE 04F03_Asynchronous_GS.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;Example by Iain McCurdy
sr = 44100
ksmps = 1
nchnls = 1
0dbfs = 1
giWave ftgen 0,0,2^10,10,1,1/2,1/4,1/8,1/16,1/32,1/64
instr 1 ;grain generating instrument 1
kRate = p4
kTrig metro kRate ; a trigger to generate grains
kDur = p5
kForm = p6
;note delay time (p2) is defined using a random function -
;- beginning with no randomization but then gradually increasing
kDelayRange transeg 0,1,0,0, p3-1,4,0.03
kDelay gauss kDelayRange
; p1 p2 p3 p4
schedkwhen kTrig,0,0,3, abs(kDelay), kDur,kForm ;trigger a note (grain) in instr 3
endin
instr 2 ;grain generating instrument 2
kRate = p4
kTrig metro kRate ; a trigger to generate grains
kDur = p5
;formant frequency (p4) is multiplied by a random function -
;- beginning with no randomization but then gradually increasing
kForm = p6
kFormOSRange transeg 0,1,0,0, p3-1,2,12 ;range defined in semitones
kFormOS gauss kFormOSRange
; p1 p2 p3 p4
schedkwhen kTrig,0,0,3, 0, kDur,kForm*semitone(kFormOS)
endin
instr 3 ;grain sounding instrument
iForm = p4
aEnv linseg 0,0.005,0.2,p3-0.01,0.2,0.005,0
aSig poscil aEnv, iForm, giWave
out aSig
endin
</CsInstruments>
<CsScore>
;p4 = rate
;p5 = duration
;p6 = formant
; p1 p2 p3 p4 p5 p6
i 1 0 12 200 0.02 400
i 2 12.5 12 200 0.02 400
e
</CsScore>
</CsoundSynthesizer>
Synthesis of Dynamic Sound Spectra: grain3
The next example introduces another of Csound's built-in granular synthesis opcodes to demonstrate the range of dynamic sound spectra that are possible with granular synthesis.
Several parameters are modulated slowly using Csound's random spline generator rspline. These parameters are formant frequency, grain duration and grain density (rate of grain generation). The waveform used in generating the content for each grain is randomly chosen using a slow sample and hold random function - a new waveform will be selected every 10 seconds. Five waveforms are provided: a sawtooth, a square wave, a triangle wave, a pulse wave and a band limited buzz-like waveform. Some of these waveforms, particularly the sawtooth, square and pulse waveforms, can generate very high overtones, for this reason a high sample rate is recommended to reduce the risk of aliasing (see chapter 01A).
Current values for formant (cps), grain duration, density and waveform are printed to the terminal every second. The key for waveforms is: 1:sawtooth; 2:square; 3:triangle; 4:pulse; 5:buzz.
EXAMPLE 04F04_grain3.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;example by Iain McCurdy
sr = 96000
ksmps = 16
nchnls = 1
0dbfs = 1
;waveforms used for granulation
giSaw ftgen 1,0,4096,7,0,4096,1
giSq ftgen 2,0,4096,7,0,2046,0,0,1,2046,1
giTri ftgen 3,0,4096,7,0,2046,1,2046,0
giPls ftgen 4,0,4096,7,1,200,1,0,0,4096-200,0
giBuzz ftgen 5,0,4096,11,20,1,1
;window function - used as an amplitude envelope for each grain
;(hanning window)
giWFn ftgen 7,0,16384,20,2,1
instr 1
;random spline generates formant values in oct format
kOct rspline 4,8,0.1,0.5
;oct format values converted to cps format
kCPS = cpsoct(kOct)
;phase location is left at 0 (the beginning of the waveform)
kPhs = 0
;frequency (formant) randomization and phase randomization are not used
kFmd = 0
kPmd = 0
;grain duration and density (rate of grain generation)
kGDur rspline 0.01,0.2,0.05,0.2
kDens rspline 10,200,0.05,0.5
;maximum number of grain overlaps allowed. This is used as a CPU brake
iMaxOvr = 1000
;function table for source waveform for content of the grain
;a different waveform chosen once every 10 seconds
kFn randomh 1,5.99,0.1
;print info. to the terminal
printks "CPS:%5.2F%TDur:%5.2F%TDensity:%5.2F%TWaveform:%1.0F%n",1,\
kCPS,kGDur,kDens,kFn
aSig grain3 kCPS, kPhs, kFmd, kPmd, kGDur, kDens, iMaxOvr, kFn, giWFn, \
0, 0
out aSig*0.06
endin
</CsInstruments>
<CsScore>
i 1 0 300
e
</CsScore>
</CsoundSynthesizer>
The final example introduces grain3's two built-in randomizing functions for phase and pitch. Phase refers to the location in the source waveform from which a grain will be read, pitch refers to the pitch of the material within grains. In this example a long note is played, initially no randomization is employed but gradually phase randomization is increased and then reduced back to zero. The same process is applied to the pitch randomization amount parameter. This time grain size is relatively large:0.8 seconds and density correspondingly low: 20 Hz.
EXAMPLE 04F05_grain3_random.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;example by Iain McCurdy
sr = 44100
ksmps = 16
nchnls = 1
0dbfs = 1
;waveforms used for granulation
giBuzz ftgen 1,0,4096,11,40,1,0.9
;window function - used as an amplitude envelope for each grain
;(bartlett window)
giWFn ftgen 2,0,16384,20,3,1
instr 1
kCPS = 100
kPhs = 0
kFmd transeg 0,21,0,0, 10,4,15, 10,-4,0
kPmd transeg 0,1,0,0, 10,4,1, 10,-4,0
kGDur = 0.8
kDens = 20
iMaxOvr = 1000
kFn = 1
;print info. to the terminal
printks "Random Phase:%5.2F%TPitch Random:%5.2F%n",1,kPmd,kFmd
aSig grain3 kCPS, kPhs, kFmd, kPmd, kGDur, kDens, iMaxOvr, kFn, giWFn, 0, 0
out aSig*0.06
endin
</CsInstruments>
<CsScore>
i 1 0 51
e
</CsScore>
</CsoundSynthesizer>
Conclusion
This chapter has introduced some of the concepts behind the synthesis of new sounds based on simple waveforms by using granular synthesis techniques. Only two of Csound's built-in opcodes for granular synthesis, fof and grain3, have been used; it is beyond the scope of this work to cover all of the many opcodes for granulation that Csound provides. This chapter has focused mainly on synchronous granular synthesis; chapter 05G, which introduces granulation of recorded sound files, makes greater use of asynchronous granular synthesis for time-stretching and pitch shifting. This chapter will also introduce some of Csound's other opcodes for granular synthesis.
PHYSICAL MODELLING
With physical modelling we employ a completely different approach to synthesis than we do with all other standard techniques. Unusually the focus is not primarily to produce a sound, but to model a physical process and if this process exhibits certain features such as periodic oscillation within a frequency range of 20 to 20000 Hz, it will produce sound.
Physical modelling synthesis techniques do not build sound using wave tables, oscillators and audio signal generators, instead they attempt to establish a model, as a system in itself, which can then produce sound because of how the system varies with time. A physical model usually derives from the real physical world, but could be any time-varying system. Physical modelling is an exciting area for the production of new sounds.
Compared with the complexity of a real-world physically dynamic system a physical model will most likely represent a brutal simplification. Nevertheless, using this technique will demand a lot of formulae, because physical models are described in terms of mathematics. Although designing a model may require some considerable work, once established the results commonly exhibit a lively tone with time-varying partials and a "natural" difference between attack and release by their very design - features that other synthesis techniques will demand more from the end user in order to establish.
Csound already contains many ready-made physical models as opcodes but you can still build your own from scratch. This chapter will look at how to implement two classical models from first principles and then introduce a number of Csound's ready made physical modelling opcodes.
The Mass-Spring Model1
Many oscillating processes in nature can be modelled as connections of masses and springs. Imagine one mass-spring unit which has been set into motion. This system can be described as a sequence of states, where every new state results from the two preceding ones. Assumed the first state a0 is 0 and the second state a1 is 0.5. Without the restricting force of the spring, the mass would continue moving unimpeded following a constant velocity:
As the velocity between the first two states can be described as a1-a0, the value of the third state a2 will be:
a2 = a1 + (a1 - a0) = 0.5 + 0.5 = 1
But, the spring pulls the mass back with a force which increases the further the mass moves away from the point of equilibrium. Therefore the masses movement can be described as the product of a constant factor c and the last position a1. This damps the continuous movement of the mass so that for a factor of c=0.4 the next position will be:
a2 = (a1 + (a1 - a0)) - c * a1 = 1 - 0.2 = 0.8
Csound can easily calculate the values by simply applying the formulae. For the first k-cycle2 , they are set via the init opcode. After calculating the new state, a1 becomes a0 and a2 becomes a1 for the next k-cycle. In the next csd the new values will be printed five times per second (the states are named here as k0/k1/k2 instead of a0/a1/a2, because k-rate values are needed for printing instead of audio samples).
EXAMPLE 04G01_Mass_spring_sine.csd
<CsoundSynthesizer> <CsOptions> -n ;no sound </CsOptions> <CsInstruments> sr = 44100 ksmps = 8820 ;5 steps per second instr PrintVals ;initial values kstep init 0 k0 init 0 k1 init 0.5 kc init 0.4 ;calculation of the next value k2 = k1 + (k1 - k0) - kc * k1 printks "Sample=%d: k0 = %.3f, k1 = %.3f, k2 = %.3f\n", 0, kstep, k0, k1, k2 ;actualize values for the next step kstep = kstep+1 k0 = k1 k1 = k2 endin </CsInstruments> <CsScore> i "PrintVals" 0 10 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
The output starts with:
State=0: k0 = 0.000, k1 = 0.500, k2 = 0.800 State=1: k0 = 0.500, k1 = 0.800, k2 = 0.780 State=2: k0 = 0.800, k1 = 0.780, k2 = 0.448 State=3: k0 = 0.780, k1 = 0.448, k2 = -0.063 State=4: k0 = 0.448, k1 = -0.063, k2 = -0.549 State=5: k0 = -0.063, k1 = -0.549, k2 = -0.815 State=6: k0 = -0.549, k1 = -0.815, k2 = -0.756 State=7: k0 = -0.815, k1 = -0.756, k2 = -0.393 State=8: k0 = -0.756, k1 = -0.393, k2 = 0.126 State=9: k0 = -0.393, k1 = 0.126, k2 = 0.595 State=10: k0 = 0.126, k1 = 0.595, k2 = 0.826 State=11: k0 = 0.595, k1 = 0.826, k2 = 0.727 State=12: k0 = 0.826, k1 = 0.727, k2 = 0.337

So, a sine wave has been created, without the use of any of Csound's oscillators...
Here is the audible proof:
EXAMPLE 04G02_MS_sine_audible.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 1
nchnls = 2
0dbfs = 1
instr MassSpring
;initial values
a0 init 0
a1 init 0.05
ic = 0.01 ;spring constant
;calculation of the next value
a2 = a1+(a1-a0) - ic*a1
outs a0, a0
;actualize values for the next step
a0 = a1
a1 = a2
endin
</CsInstruments>
<CsScore>
i "MassSpring" 0 10
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz, after martin neukom
As the next sample is calculated in the next control cycle, ksmps has to be set to 1.3 The resulting frequency depends on the spring constant: the higher the constant, the higher the frequency. The resulting amplitude depends on both, the starting value and the spring constant.
This simple model shows the basic principle of a physical modelling synthesis: creating a system which produces sound because it varies in time. Certainly it is not the goal of physical modelling synthesis to reinvent the wheel of a sine wave. But modulating the parameters of a model may lead to interesting results. The next example varies the spring constant, which is now no longer a constant:
EXAMPLE 04G03_MS_variable_constant.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 1
nchnls = 2
0dbfs = 1
instr MassSpring
;initial values
a0 init 0
a1 init 0.05
kc randomi .001, .05, 8, 3
;calculation of the next value
a2 = a1+(a1-a0) - kc*a1
outs a0, a0
;actualize values for the next step
a0 = a1
a1 = a2
endin
</CsInstruments>
<CsScore>
i "MassSpring" 0 10
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Working with physical modelling demands thought in more physical or mathematical terms: examples of this might be if you were to change the formula when a certain value of c had been reached, or combine more than one spring.
Implementing Simple Physical Systems
This text shows how to get oscillators and filters from simple physical models by recording the position of a point (mass) of a physical system. The behavior of a particle (mass on a spring, mass of a pendulum, etc.) is described by its position, velocity and acceleration. The mathematical equations, which describe the movement of such a point, are differential equations. In what follows, we describe how to derive time discrete system equations (also called difference equations) from physical models (described by differential equations). At every time step we first calculate the acceleration of a mass and then its new velocity and position. This procedure is called Euler's method and yields good results for low frequencies compared to the sampling rate (better approximations are achieved with the improved Euler's method or the Runge–Kutta methods).
The figures below have been realized with Mathematica.
Integrating the Trajectory of a Point
Velocity v is the difference of positions x per time unit T, acceleration a the difference of velocities v per time unit T:
vt = (xt – xt-1)/T, at = (vt – vt-1)/T.
Putting T = 1 we get
vt = xt – xt-1, at = vt – vt-1.
If we know the position and velocity of a point at time t – 1 and are able to calculate its acceleration at time t we can calculate the velocity vt and the position xt at time t:
vt = vt-1 + at andxt = xt-1 + vt
With the following algorithm we calculate a sequence of successive positions x:
1. init x and v 2. calculate a 3. v += a ; v = v + a 4. x += v ; x = x + v
Example 1: The acceleration of gravity is constant (g = –9.81ms-2). For a mass with initial position x = 300m (above ground) and velocity v = 70ms-1 (upwards) we get the following trajectory (path)
g = -9.81; x = 300; v = 70; Table[v += g; x += v, {16}];
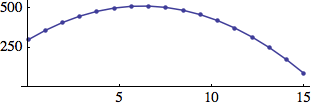
Example 2: The acceleration a of a mass on a spring is proportional (with factor –c) to its position (deflection) x.
x = 0; v = 1; c = .3; Table[a = -c*x; v += a; x += v, {22}];
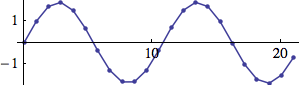
Introducing damping
Since damping is proportional to the velocity we reduce velocity at every time step by a certain amount d:
v *= (1 - d)
Example 3: Spring with damping (see lin_reson.csd below):
d = 0.2; c = .3; x = 0; v = 1;
Table[a = -c*x; v += a; v *= (1 - d); x += v, {22}];
The factor c can be calculated from the frequency f:
c = 2 – sqrt(4 – d2) cos(2π f/sr)
Introducing excitation
In the examples 2 and 3 the systems oscillate because of their initial velocity v = 1. The resultant oscillation is the impulse response of the systems. We can excite the systems continuously by adding a value exc to the velocity at every time step.
v += exc;
Example 4: Damped spring with random excitation (resonator with noise as input)
d = .01; s = 0; v = 0; Table[a = -.3*s; v += a; v += RandomReal[{-1, 1}]; v *= (1 - d); s += v, {61}];
EXAMPLE 04G04_lin_reson.csd
<CsoundSynthesizer> <CsInstruments> sr = 44100 ksmps = 32 nchnls = 1 0dbfs = 1 opcode lin_reson, a, akk setksmps 1 avel init 0 ;velocity ax init 0 ;deflection x ain,kf,kdamp xin kc = 2-sqrt(4-kdamp^2)*cos(kf*2*$M_PI/sr) aacel = -kc*ax avel = avel+aacel+ain avel = avel*(1-kdamp) ax = ax+avel xout ax endop instr 1 aexc rand p4 aout lin_reson aexc,p5,p6 out aout endin </CsInstruments> <CsScore> ; p4 p5 p6 ; excitaion freq damping i1 0 5 .0001 440 .0001 </CsScore> </CsoundSynthesizer> ;example by martin neukom
Introducing nonlinear acceleration
Example 5: The acceleration of a pendulum depends on its deflection (angle x).
a = c*sin(x)
This figure shows the function –.3sin(x)
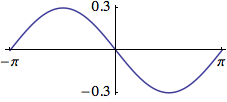
The following trajectory shows that the frequency decreases with encreasing amplitude and that the pendulum can turn around.
d = .003; s = 0; v = 0;
Table[a = f[s]; v += a; v += RandomReal[{-.09, .1}]; v *= (1 - d);
s += v, {400}];
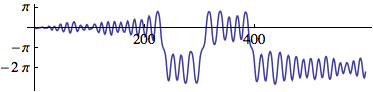
We can implement systems with accelerations that are arbitrary functions of position x.
Example 6: a = f(x) = – c1x + c2sin(c3x)
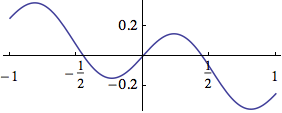
d = .03; x = 0; v = 0; Table[a = f[x]; v += a; v += RandomReal[{-.1, .1}]; v *= (1 - d); x += v, {400}];
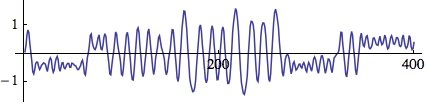
EXAMPLE 04G05_nonlin_reson.csd
<CsoundSynthesizer> <CsInstruments> sr = 44100 ksmps = 32 nchnls = 1 0dbfs = 1 ; simple damped nonlinear resonator opcode nonlin_reson, a, akki setksmps 1 avel init 0 ;velocity adef init 0 ;deflection ain,kc,kdamp,ifn xin aacel tablei adef, ifn, 1, .5 ;acceleration = -c1*f1(def) aacel = -kc*aacel avel = avel+aacel+ain ;vel += acel + excitation avel = avel*(1-kdamp) adef = adef+avel xout adef endop instr 1 kenv oscil p4,.5,1 aexc rand kenv aout nonlin_reson aexc,p5,p6,p7 out aout endin </CsInstruments> <CsScore> f1 0 1024 10 1 f2 0 1024 7 -1 510 .15 4 -.15 510 1 f3 0 1024 7 -1 350 .1 100 -.3 100 .2 100 -.1 354 1 ; p4 p5 p6 p7 ; excitation c1 damping ifn i1 0 20 .0001 .01 .00001 3 ;i1 0 20 .0001 .01 .00001 2 </CsScore> </CsoundSynthesizer> ;example by martin neukom
The Van der Pol Oscillator
While attempting to explain the nonlinear dynamics of vacuum tube circuits, the Dutch electrical engineer Balthasar van der Pol derived the differential equation
d2x/dt2 = –ω2x + μ(1 – x2)dx/dt. (where d2x/dt2 = acelleration and dx/dt = velocity)
The equation describes a linear oscillator d2x/dt2 = –ω2x with an additional nonlinear term μ(1 – x2)dx/dt. When |x| > 1, the nonlinear term results in damping, but when |x| < 1, negative damping results, which means that energy is introduced into the system.
Such oscillators compensating for energy loss by an inner energy source are called self-sustained oscillators.
v = 0; x = .001; ω = 0.1; μ = 0.25;
snd = Table[v += (-ω^2*x + μ*(1 - x^2)*v); x += v, {200}];

The constant ω is the angular frequency of the linear oscillator (μ = 0). For a simulation with sampling rate sr we calculate the frequency f in Hz as
f = ω·sr/2π.
Since the simulation is only an approximation of the oscillation this formula gives good results only for low frequencies. The exact frequency of the simulation is
f = arccos(1 – ω2/2)sr·/2π.
We get ω2 from frequency f as
2 – 2cos(f·2π/sr).
With increasing μ the oscillations nonlinearity becomes stronger and more overtones arise (and at the same time the frequency becomes lower). The following figure shows the spectrum of the oscillation for various values of μ.
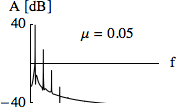
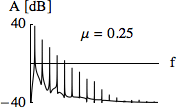
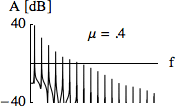
Certain oscillators can be synchronized either by an external force or by mutual influence. Examples of synchronization by an external force are the control of cardiac activity by a pace maker and the adjusting of a clock by radio signals. An example for the mutual synchronization of oscillating systems is the coordinated clapping of an audience. These systems have in common that they are not linear and that they oscillate without external excitation (self-sustained oscillators).
The UDO v_d_p represents a Van der Pol oscillator with a natural frequency kfr and a nonlinearity factor kmu. It can be excited by a sine wave of frequency kfex and amplitude kaex. The range of frequency within which the oscillator is synchronized to the exciting frequency increases as kmu and kaex increase.
EXAMPLE 04G06_van_der_pol.csd
<CsoundSynthesizer>
<CsOptions> -odac </CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
;Van der Pol Oscillator ;outputs a nonliniear oscillation
;inputs: a_excitation, k_frequency in Hz (of the linear part), nonlinearity (0 < mu < ca. 0.7)
opcode v_d_p, a, akk
setksmps 1
av init 0
ax init 0
ain,kfr,kmu xin
kc = 2-2*cos(kfr*2*$M_PI/sr)
aa = -kc*ax + kmu*(1-ax*ax)*av
av = av + aa
ax = ax + av + ain
xout ax
endop
instr 1
kaex = .001
kfex = 830
kamp = .15
kf = 455
kmu linseg 0,p3,.7
a1 poscil kaex,kfex
aout v_d_p a1,kf,kmu
out kamp*aout,a1*100
endin
</CsInstruments>
<CsScore>
i1 0 20
</CsScore>
</CsoundSynthesizer>
;example by martin neukom, adapted by joachim heintz
The variation of the phase difference between excitation and oscillation, as well as the transitions between synchronous, beating and asynchronous behaviors, can be visualized by showing the sum of the excitation and the oscillation signals in a phase diagram. The following figures show to the upper left the waveform of the Van der Pol oscillator, to the lower left that of the excitation (normalized) and to the right the phase diagram of their sum. For these figures, the same values were always used for kfr, kmu and kaex. Comparing the first two figures, one sees that the oscillator adopts the exciting frequency kfex within a large frequency range. When the frequency is low (figure a), the phases of the two waves are nearly the same. Hence there is a large deflection along the x-axis in the phase diagram showing the sum of the waveforms. When the frequency is high, the phases are nearly inverted (figure b) and the phase diagram shows only a small deflection. The figure c shows the transition to asynchronous behavior. If the proportion between the natural frequency of the oscillator kfr and the excitation frequency kfex is approximately simple (kfex/kfr ≅ m/n), then within a certain range the frequency of the Van der Pol oscillator is synchronized so that kfex/kfr = m/n. Here one speaks of higher order synchronization (figure d).
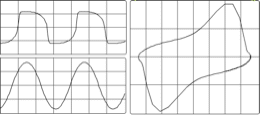
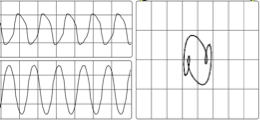
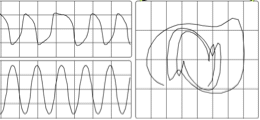
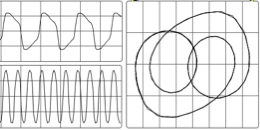
The Karplus-Strong Algorithm: Plucked String
The Karplus-Strong algorithm provides another simple yet interesting example of how physical modelling can be used to synthesized sound. A buffer is filled with random values of either +1 or -1. At the end of the buffer, the mean of the first and the second value to come out of the buffer is calculated. This value is then put back at the beginning of the buffer, and all the values in the buffer are shifted by one position.
This is what happens for a buffer of five values, for the first five steps:
| initial state | 1 | -1 | 1 | 1 | -1 |
| step 1 | 0 | 1 | -1 | 1 | 1 |
| step 2 | 1 | 0 | 1 | -1 | 1 |
| step 3 | 0 | 1 | 0 | 1 | -1 |
| step 4 | 0 | 0 | 1 | 0 | 1 |
| step 5 | 0.5 | 0 | 0 | 1 | 0 |
The next Csound example represents the content of the buffer in a function table, implements and executes the algorithm, and prints the result after each five steps which here is referred to as one cycle:
EXAMPLE 04G07_KarplusStrong.csd
<CsoundSynthesizer>
<CsOptions>
-n
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
opcode KS, 0, ii
;performs the karplus-strong algorithm
iTab, iTbSiz xin
;calculate the mean of the last two values
iUlt tab_i iTbSiz-1, iTab
iPenUlt tab_i iTbSiz-2, iTab
iNewVal = (iUlt + iPenUlt) / 2
;shift values one position to the right
indx = iTbSiz-2
loop:
iVal tab_i indx, iTab
tabw_i iVal, indx+1, iTab
loop_ge indx, 1, 0, loop
;fill the new value at the beginning of the table
tabw_i iNewVal, 0, iTab
endop
opcode PrintTab, 0, iiS
;prints table content, with a starting string
iTab, iTbSiz, Sin xin
indx = 0
Sout strcpy Sin
loop:
iVal tab_i indx, iTab
Snew sprintf "%8.3f", iVal
Sout strcat Sout, Snew
loop_lt indx, 1, iTbSiz, loop
puts Sout, 1
endop
instr ShowBuffer
;fill the function table
iTab ftgen 0, 0, -5, -2, 1, -1, 1, 1, -1
iTbLen tableng iTab
;loop cycles (five states)
iCycle = 0
cycle:
Scycle sprintf "Cycle %d:", iCycle
PrintTab iTab, iTbLen, Scycle
;loop states
iState = 0
state:
KS iTab, iTbLen
loop_lt iState, 1, iTbLen, state
loop_lt iCycle, 1, 10, cycle
endin
</CsInstruments>
<CsScore>
i "ShowBuffer" 0 1
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
This is the output:
Cycle 0: 1.000 -1.000 1.000 1.000 -1.000 Cycle 1: 0.500 0.000 0.000 1.000 0.000 Cycle 2: 0.500 0.250 0.000 0.500 0.500 Cycle 3: 0.500 0.375 0.125 0.250 0.500 Cycle 4: 0.438 0.438 0.250 0.188 0.375 Cycle 5: 0.359 0.438 0.344 0.219 0.281 Cycle 6: 0.305 0.398 0.391 0.281 0.250 Cycle 7: 0.285 0.352 0.395 0.336 0.266 Cycle 8: 0.293 0.318 0.373 0.365 0.301 Cycle 9: 0.313 0.306 0.346 0.369 0.333
It can be seen clearly that the values get smoothed more and more from cycle to cycle. As the buffer size is very small here, the values tend to come to a constant level; in this case 0.333. But for larger buffer sizes, after some cycles the buffer content has the effect of a period which is repeated with a slight loss of amplitude. This is how it sounds, if the buffer size is 1/100 second (or 441 samples at sr=44100):
EXAMPLE 04G08_Plucked.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 1
nchnls = 2
0dbfs = 1
instr 1
;delay time
iDelTm = 0.01
;fill the delay line with either -1 or 1 randomly
kDur timeinsts
if kDur < iDelTm then
aFill rand 1, 2, 1, 1 ;values 0-2
aFill = floor(aFill)*2 - 1 ;just -1 or +1
else
aFill = 0
endif
;delay and feedback
aUlt init 0 ;last sample in the delay line
aUlt1 init 0 ;delayed by one sample
aMean = (aUlt+aUlt1)/2 ;mean of these two
aUlt delay aFill+aMean, iDelTm
aUlt1 delay1 aUlt
outs aUlt, aUlt
endin
</CsInstruments>
<CsScore>
i 1 0 60
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz, after martin neukom
This sound resembles a plucked string: at the beginning the sound is noisy but after a short period of time it exhibits periodicity. As can be heard, unless a natural string, the steady state is virtually endless, so for practical use it needs some fade-out. The frequency the listener perceives is related to the length of the delay line. If the delay line is 1/100 of a second, the perceived frequency is 100 Hz. Compared with a sine wave of similar frequency, the inherent periodicity can be seen, and also the rich overtone structure:
Csound also contains over forty opcodes which provide a wide variety of ready-made physical models and emulations. A small number of them will be introduced here to give a brief overview of the sort of things available.
wgbow - A Waveguide Emulation of a Bowed String by Perry Cook
Perry Cook is a prolific author of physical models and a lot of his work has been converted into Csound opcodes. A number of these models wgbow, wgflute, wgclar wgbowedbar and wgbrass are based on waveguides. A waveguide, in its broadest sense, is some sort of mechanism that limits the extend of oscillations, such as a vibrating string fixed at both ends or a pipe. In these sorts of physical model a delay is used to emulate these limits. One of these, wgbow, implements an emulation of a bowed string. Perhaps the most interesting aspect of many physical models in not specifically whether they emulate the target instrument played in a conventional way accurately but the facilities they provide for extending the physical limits of the instrument and how it is played - there are already vast sample libraries and software samplers for emulating conventional instruments played conventionally. wgbow offers several interesting options for experimentation including the ability to modulate the bow pressure and the bowing position at k-rate. Varying bow pressure will change the tone of the sound produced by changing the harmonic emphasis. As bow pressure reduces, the fundamental of the tone becomes weaker and overtones become more prominent. If the bow pressure is reduced further the abilty of the system to produce a resonance at all collapse. This boundary between tone production and the inability to produce a tone can provide some interesting new sound effect. The following example explores this sound area by modulating the bow pressure parameter around this threshold. Some additional features to enhance the example are that 7 different notes are played simultaneously, the bow pressure modulations in the right channel are delayed by a varying amount with respect top the left channel in order to create a stereo effect and a reverb has been added.
EXAMPLE 04G09_wgbow.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0
gisine ftgen 0,0,4096,10,1
gaSendL,gaSendR init 0
instr 1 ; wgbow instrument
kamp = 0.3
kfreq = p4
ipres1 = p5
ipres2 = p6
; kpres (bow pressure) defined using a random spline
kpres rspline p5,p6,0.5,2
krat = 0.127236
kvibf = 4.5
kvibamp = 0
iminfreq = 20
; call the wgbow opcode
aSigL wgbow kamp,kfreq,kpres,krat,kvibf,kvibamp,gisine,iminfreq
; modulating delay time
kdel rspline 0.01,0.1,0.1,0.5
; bow pressure parameter delayed by a varying time in the right channel
kpres vdel_k kpres,kdel,0.2,2
aSigR wgbow kamp,kfreq,kpres,krat,kvibf,kvibamp,gisine,iminfreq
outs aSigL,aSigR
; send some audio to the reverb
gaSendL = gaSendL + aSigL/3
gaSendR = gaSendR + aSigR/3
endin
instr 2 ; reverb
aRvbL,aRvbR reverbsc gaSendL,gaSendR,0.9,7000
outs aRvbL,aRvbR
clear gaSendL,gaSendR
endin
</CsInstruments>
<CsScore>
; instr. 1
; p4 = pitch (hz.)
; p5 = minimum bow pressure
; p6 = maximum bow pressure
; 7 notes played by the wgbow instrument
i 1 0 480 70 0.03 0.1
i 1 0 480 85 0.03 0.1
i 1 0 480 100 0.03 0.09
i 1 0 480 135 0.03 0.09
i 1 0 480 170 0.02 0.09
i 1 0 480 202 0.04 0.1
i 1 0 480 233 0.05 0.11
; reverb instrument
i 2 0 480
</CsScore>
</CsoundSynthesizer>
This time a stack of eight sustaining notes, each separated by an octave, vary their 'bowing position' randomly and independently. You will hear how different bowing positions accentuates and attenuates different partials of the bowing tone. To enhance the sound produced some filtering with tone and pareq is employed and some reverb is added.
EXAMPLE 04G10_wgbow_enhanced.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0
gisine ftgen 0,0,4096,10,1
gaSend init 0
instr 1 ; wgbow instrument
kamp = 0.1
kfreq = p4
kpres = 0.2
krat rspline 0.006,0.988,0.1,0.4
kvibf = 4.5
kvibamp = 0
iminfreq = 20
aSig wgbow kamp,kfreq,kpres,krat,kvibf,kvibamp,gisine,iminfreq
aSig butlp aSig,2000
aSig pareq aSig,80,6,0.707
outs aSig,aSig
gaSend = gaSend + aSig/3
endin
instr 2 ; reverb
aRvbL,aRvbR reverbsc gaSend,gaSend,0.9,7000
outs aRvbL,aRvbR
clear gaSend
endin
</CsInstruments>
<CsScore>
; instr. 1 (wgbow instrument)
; p4 = pitch (hertz)
; wgbow instrument
i 1 0 480 20
i 1 0 480 40
i 1 0 480 80
i 1 0 480 160
i 1 0 480 320
i 1 0 480 640
i 1 0 480 1280
i 1 0 480 2460
; reverb instrument
i 2 0 480
</CsScore>
</CsoundSynthesizer>
All of the wg- family of opcodes are worth exploring and often the approach taken here - exploring each input parameter in isolation whilst the others retain constant values - sets the path to understanding the model better. Tone production with wgbrass is very much dependent upon the relationship between intended pitch and lip tension, random experimentation with this opcode is as likely to result in silence as it is in sound and in this way is perhaps a reflection of the experience of learning a brass instrument when the student spends most time push air silently through the instrument. With patience it is capable of some interesting sounds however. In its case, I would recommend building a realtime GUI and exploring the interaction of its input arguments that way. wgbowedbar, like a number of physical modelling algorithms, is rather unstable. This is not necessary a design flaw in the algorithm but instead perhaps an indication that the algorithm has been left quite open for out experimentation - or abuse. In these situation caution is advised in order to protect ears and loudspeakers. Positive feedback within the model can result in signals of enormous amplitude very quickly. Employment of the clip opcode as a means of some protection is recommended when experimenting in realtime.
barmodel - a Model of a Struck Metal Bar by Stefan Bilbao
barmodel can also imitate wooden bars, tubular bells, chimes and other resonant inharmonic objects. barmodel is a model that can easily be abused to produce ear shreddingly loud sounds therefore precautions are advised when experimenting with it in realtime. We are presented with a wealth of input arguments such as 'stiffness', 'strike position' and 'strike velocity', which relate in an easily understandable way to the physical process we are emulating. Some parameters will evidently have more of a dramatic effect on the sound produced than other and again it is recommended to create a realtime GUI for exploration. Nonetheless, a fixed example is provided below that should offer some insight into the kinds of sounds possible.
Probably the most important parameter for us is the stiffness of the bar. This actually provides us with our pitch control and is not in cycle-per-second so some experimentation will be required to find a desired pitch. There is a relationship between stiffness and the parameter used to define the width of the strike - when the stiffness coefficient is higher a wider strike may be required in order for the note to sound. Strike width also impacts upon the tone produced, narrower strikes generating emphasis upon upper partials (provided a tone is still produced) whilst wider strikes tend to emphasize the fundamental).
The parameter for strike position also has some impact upon the spectral balance. This effect may be more subtle and may be dependent upon some other parameter settings, for example, when strike width is particularly wide, its effect may be imperceptible. A general rule of thumb here is that in order to achieve the greatest effect from strike position, strike width should be as low as will still produce a tone. This kind of interdependency between input parameters is the essence of working with a physical model that can be both intriguing and frustrating.
An important parameter that will vary the impression of the bar from metal to wood is
An interesting feature incorporated into the model in the ability to modulate the point along the bar at which vibrations are read. This could also be described as pick-up position. Moving this scanning location results in tonal and amplitude variations. We just have control over the frequency at which the scanning location is modulated.
EXAMPLE 04G11_barmodel.csd
<CsoundSynthesizer> <CsOptions> -odac </CsOptions> <CsInstruments> sr = 44100 ksmps = 32 nchnls = 2 0dbfs = 1 instr 1 ; boundary conditions 1=fixed 2=pivot 3=free kbcL = 1 kbcR = 1 ; stiffness iK = p4 ; high freq. loss (damping) ib = p5 ; scanning frequency kscan rspline p6,p7,0.2,0.8 ; time to reach 30db decay iT30 = p3 ; strike position ipos random 0,1 ; strike velocity ivel = 1000 ; width of strike iwid = 0.1156 aSig barmodel kbcL,kbcR,iK,ib,kscan,iT30,ipos,ivel,iwid kPan rspline 0.1,0.9,0.5,2 aL,aR pan2 aSig,kPan outs aL,aR endin </CsInstruments> <CsScore> ;t 0 90 1 30 2 60 5 90 7 30 ; p4 = stiffness (pitch) #define gliss(dur'Kstrt'Kend'b'scan1'scan2) # i 1 0 20 $Kstrt $b $scan1 $scan2 i 1 ^+0.05 $dur > $b $scan1 $scan2 i 1 ^+0.05 $dur > $b $scan1 $scan2 i 1 ^+0.05 $dur > $b $scan1 $scan2 i 1 ^+0.05 $dur > $b $scan1 $scan2 i 1 ^+0.05 $dur > $b $scan1 $scan2 i 1 ^+0.05 $dur > $b $scan1 $scan2 i 1 ^+0.05 $dur > $b $scan1 $scan2 i 1 ^+0.05 $dur > $b $scan1 $scan2 i 1 ^+0.05 $dur > $b $scan1 $scan2 i 1 ^+0.05 $dur > $b $scan1 $scan2 i 1 ^+0.05 $dur > $b $scan1 $scan2 i 1 ^+0.05 $dur > $b $scan1 $scan2 i 1 ^+0.05 $dur > $b $scan1 $scan2 i 1 ^+0.05 $dur > $b $scan1 $scan2 i 1 ^+0.05 $dur > $b $scan1 $scan2 i 1 ^+0.05 $dur > $b $scan1 $scan2 i 1 ^+0.05 $dur $Kend $b $scan1 $scan2 # $gliss(15'40'400'0.0755'0.1'2) b 5 $gliss(2'80'800'0.755'0'0.1) b 10 $gliss(3'10'100'0.1'0'0) b 15 $gliss(40'40'433'0'0.2'5) e </CsScore> </CsoundSynthesizer> ; example written by Iain McCurdy
PhISEM - Physically Inspired Stochastic Event Modeling
The PhiSEM set of models in Csound, again based on the work of Perry Cook, imitate instruments that rely on collisions between smaller sound producing object to produce their sounds. These models include a tambourine, a set of bamboo windchimes and sleighbells. These models algorithmically mimic these multiple collisions internally so that we only need to define elements such as the number of internal elements (timbrels, beans, bells etc.) internal damping and resonances. Once again the most interesting aspect of working with a model is to stretch the physical limits so that we can hear the results from, for example, a maraca with an impossible number of beans, a tambourine with so little internal damping that it never decays. In the following example I explore tambourine, bamboo and sleighbells each in turn, first in a state that mimics the source instrument and then with some more extreme conditions.
EXAMPLE 04G12_PhiSEM.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
instr 1 ; tambourine
iAmp = p4
iDettack = 0.01
iNum = p5
iDamp = p6
iMaxShake = 0
iFreq = p7
iFreq1 = p8
iFreq2 = p9
aSig tambourine iAmp,iDettack,iNum,iDamp,iMaxShake,iFreq,iFreq1,iFreq2
out aSig
endin
instr 2 ; bamboo
iAmp = p4
iDettack = 0.01
iNum = p5
iDamp = p6
iMaxShake = 0
iFreq = p7
iFreq1 = p8
iFreq2 = p9
aSig bamboo iAmp,iDettack,iNum,iDamp,iMaxShake,iFreq,iFreq1,iFreq2
out aSig
endin
instr 3 ; sleighbells
iAmp = p4
iDettack = 0.01
iNum = p5
iDamp = p6
iMaxShake = 0
iFreq = p7
iFreq1 = p8
iFreq2 = p9
aSig sleighbells iAmp,iDettack,iNum,iDamp,iMaxShake,iFreq,iFreq1,iFreq2
out aSig
endin
</CsInstruments>
<CsScore>
; p4 = amp.
; p5 = number of timbrels
; p6 = damping
; p7 = freq (main)
; p8 = freq 1
; p9 = freq 2
; tambourine
i 1 0 1 0.1 32 0.47 2300 5600 8100
i 1 + 1 0.1 32 0.47 2300 5600 8100
i 1 + 2 0.1 32 0.75 2300 5600 8100
i 1 + 2 0.05 2 0.75 2300 5600 8100
i 1 + 1 0.1 16 0.65 2000 4000 8000
i 1 + 1 0.1 16 0.65 1000 2000 3000
i 1 8 2 0.01 1 0.75 1257 2653 6245
i 1 8 2 0.01 1 0.75 673 3256 9102
i 1 8 2 0.01 1 0.75 314 1629 4756
b 10
; bamboo
i 2 0 1 0.4 1.25 0.0 2800 2240 3360
i 2 + 1 0.4 1.25 0.0 2800 2240 3360
i 2 + 2 0.4 1.25 0.05 2800 2240 3360
i 2 + 2 0.2 10 0.05 2800 2240 3360
i 2 + 1 0.3 16 0.01 2000 4000 8000
i 2 + 1 0.3 16 0.01 1000 2000 3000
i 2 8 2 0.1 1 0.05 1257 2653 6245
i 2 8 2 0.1 1 0.05 1073 3256 8102
i 2 8 2 0.1 1 0.05 514 6629 9756
b 20
; sleighbells
i 3 0 1 0.7 1.25 0.17 2500 5300 6500
i 3 + 1 0.7 1.25 0.17 2500 5300 6500
i 3 + 2 0.7 1.25 0.3 2500 5300 6500
i 3 + 2 0.4 10 0.3 2500 5300 6500
i 3 + 1 0.5 16 0.2 2000 4000 8000
i 3 + 1 0.5 16 0.2 1000 2000 3000
i 3 8 2 0.3 1 0.3 1257 2653 6245
i 3 8 2 0.3 1 0.3 1073 3256 8102
i 3 8 2 0.3 1 0.3 514 6629 9756
e
</CsScore>
</CsoundSynthesizer>
; example written by Iain McCurdy
Physical modelling can produce rich, spectrally dynamic sounds with user manipulation usually abstracted to a small number of descriptive parameters. Csound offers a wealth of other opcodes for physical modelling which cannot all be introduced here so the user is encouraged to explore based on the approaches exemplified here. You can find lists in the chapters Models and Emulations, Scanned Synthesis and Waveguide Physical Modeling of the Csound Manual.
- The explanation here follows chapter 8.1.1 of Martin Neukom's Signale Systeme Klangsynthese (Bern 2003)^
- See chapter 03A INITIALIZATION AND PERFORMANCE PASS for more information about Csound's performance loops.^
- If defining this as a UDO, a local ksmps=1 could be set without affecting the general ksmps. See chapter 03F USER DEFINED OPCODES and the Csound Manual for setksmps for more information.^
SCANNED SYNTHESIS
Scanned Synthesis is a relatively new synthesis technique invented by Max Mathews, Rob Shaw and Bill Verplank at Interval Research in 2000. This algorithm uses a combination of a table-lookup oscillator and Sir Issac Newton's mechanical model (equation) of a mass and spring system to dynamically change the values stored in an f-table. The sonic result is a timbral spectrum that changes with time.
Csound has a couple opcodes dedicated to scanned synthesis, and these opcodes can be used not only to make sounds, but also to generate dynamic f-tables for use with other Csound opcodes.
A QUICK SCANNED SYNTH
The quickest way to start using scanned synthesis is Matt Ingalls' opcode scantable.
a1 scantable iamp, kfrq, ipos, imass, istiff, idamp, ivel
The arguments iamp and kfrq should be familiar, amplitude and frequency respectively. The other arguments are f-table numbers containing data known in the scanned synthesis world as profiles.
PROFILES
Profiles refer to variables in the mass and spring equation. Newton's model describes a string as a finite series of marbles connected to each other with springs.
In this example we will use 128 marbles in our system. To the Csound user, profiles are a series of f-tables that set up the scantable opcode. To the opcode, these f-tables influence the dynamic behavior of the table read by a table-lookup oscillator.
gipos ftgen 1, 0, 128, 10, 1 ;Initial Shape: Sine wave range -1 to 1
gimass ftgen 2, 0, 128, -7, 1, 1 ;Masses: Constant value 1
gistiff ftgen 3, 0, 128, -7, 50, 64, 100, 64, 0 ;Stiffness: Unipolar triangle range to 100
gidamp ftgen 4, 0, 128, -7, 1, 128, 1 ;Damping: Constant value 1
givel ftgen 5, 0, 128, -7, 0, 128, 0 ;Initial Velocity: Constant value 0 These tables need to be the same size as each other or Csound will return an error.
Run the following .csd. Notice that the sound starts off sounding like our intial shape (a sine wave) but evolves as if there are filters, distortions or LFO's.
EXAMPLE 04H01_scantable.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
nchnls = 2
sr=44100
ksmps = 32
0dbfs = 1
gipos ftgen 1, 0, 128, 10, 1 ;Initial Shape, sine wave range -1 to 1
gimass ftgen 2, 0, 128, -7, 1, 128, 1 ;Masses(adj.), constant value 1
gistiff ftgen 3, 0, 128, -7, 50, 64, 100, 64, 0 ;Stiffness; unipolar triangle range 0 to 100
gidamp ftgen 4, 0, 128, -7, 1, 128, 1 ;Damping; constant value 1
givel ftgen 5, 0, 128, -7, 0, 128, 0 ;Initial Velocity; constant value 0
instr 1
iamp = .7
kfrq = 440
a1 scantable iamp, kfrq, gipos, gimass, gistiff, gidamp, givel
a1 dcblock2 a1
outs a1, a1
endin
</CsInstruments>
<CsScore>
i 1 0 10
e
</CsScore>
</CsoundSynthesizer>
;Example by Christopher Saunders
But as you see no effects or control signals in the .csd, just a synth!
This is the power of scanned synthesis. It produces a dynamic spectrum with "just" an oscillator. Imagine now applying a scanned synthesis oscillator to all your favorite synth techniques - Subtractive, Waveshaping, FM, Granular and more.
Recall from the subtractive synthesis technique, that the "shape" of the waveform of your oscillator has a huge effect on the way the oscillator sounds. In scanned synthesis, the shape is in motion and these f-tables control how the shape moves.
DYNAMIC TABLES
The scantable opcode makes it easy to use dynamic f-tables in other csound opcodes. The example below sounds exactly like the above .csd, but it demonstrates how the f-table set into motion by scantable can be used by other csound opcodes.
EXAMPLE 04H02_Dynamic_tables.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
nchnls = 2
sr=44100
ksmps = 32
0dbfs = 1
gipos ftgen 1, 0, 128, 10, 1 ;Initial Shape, sine wave range -1 to 1;
gimass ftgen 2, 0, 128, -7, 1, 128, 1 ;Masses(adj.), constant value 1
gistiff ftgen 3, 0, 128, -7, 50, 64, 100, 64, 0 ;Stiffness; unipolar triangle range 0 to 100
gidamp ftgen 4, 0, 128, -7, 1, 128, 1 ;Damping; constant value 1
givel ftgen 5, 0, 128, -7, 0, 128, 0 ;Initial Velocity; constant value 0
instr 1
iamp = .7
kfrq = 440
a0 scantable iamp, kfrq, gipos, gimass, gistiff, gidamp, givel ;
a1 oscil3 iamp, kfrq, gipos
a1 dcblock2 a1
outs a1, a1
endin
</CsInstruments>
<CsScore>
i 1 0 10
e
</CsScore>
</CsoundSynthesizer>
;Example by Christopher Saunders
Above we use a table-lookup oscillator to periodically read a dynamic table.
Below is an example of using the values of an f-table generated by scantable, to modify the amplitudes of an fsig, a signal type in csound which represents a spectral signal.
EXAMPLE 04H03_Scantable_pvsmaska.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
nchnls = 2
sr=44100
ksmps = 32
0dbfs = 1
gipos ftgen 1, 0, 128, 10, 1 ;Initial Shape, sine wave range -1 to 1;
gimass ftgen 2, 0, 128, -7, 1, 128, 1 ;Masses(adj.), constant value 1
gistiff ftgen 3, 0, 128, -7, 50, 64, 100, 64, 0 ;Stiffness; unipolar triangle range 0 to 100
gidamp ftgen 4, 0, 128, -7, 1, 128, 1 ;Damping; constant value 1
givel ftgen 5, 0, 128, -7, 0, 128, 0 ;Initial Velocity; constant value 0
gisin ftgen 6, 0,8192, 10, 1 ;Sine wave for buzz opcode
instr 1
iamp = .7
kfrq = 110
a1 buzz iamp, kfrq, 32, gisin
outs a1, a1
endin
instr 2
iamp = .7
kfrq = 110
a0 scantable 1, 10, gipos, gimass, gistiff, gidamp, givel ;
ifftsize = 128
ioverlap = ifftsize / 4
iwinsize = ifftsize
iwinshape = 1; von-Hann window
a1 buzz iamp, kfrq, 32, gisin
fftin pvsanal a1, ifftsize, ioverlap, iwinsize, iwinshape; fft-analysis of file
fmask pvsmaska fftin, 1, 1
a2 pvsynth fmask; resynthesize
outs a2, a2
endin
</CsInstruments>
<CsScore>
i 1 0 3
i 2 5 10
e
</CsScore>
</CsoundSynthesizer>
;Example by Christopher Saunders</code>
In this .csd, the score plays instrument 1, a normal buzz sound, and then the score plays instrument 2 -- the same buzz sound re-synthesized with amplitudes of each of the 128 frequency bands, controlled by a dynamic f-table.
A MORE FLEXIBLE SCANNED SYNTH
Scantable can do a lot for us, it can synthesize an interesting, time-varying timbre using a table lookup oscillator, or animate an f-table for use in other Csound opcodes. However, there are other scanned synthesis opcodes that can take our expressive use of the algorithm even further.
The opcodes scans and scanu by Paris Smaragdis give the Csound user one of the most robust and flexible scanned synthesis environments. These opcodes work in tandem to first set up the dynamic wavetable, and then to "scan" the dynamic table in ways a table-lookup oscillator cannot.
The opcode scanu takes 18 arguments and sets a table into motion.
scanu ipos, irate, ifnvel, ifnmass, ifnstif, ifncentr, ifndamp, kmass, kstif, kcentr, kdamp, ileft, iright, kpos, kstrngth, ain, idisp, id
For a detailed description of what each argument does, see the Csound Reference Manual; I will discuss the various types of arguments in the opcode.
The first set of arguments - ipos, irate, ifnvel, ifnmass, ifnstiff, ifncenter, and ifndamp - are f-tables describing the profiles, similar to the profile arguments for scantable. Scanu takes 6 f-tables instead of scantable's 5. Like scantable, these need to be f-tables of the same size, or Csound will return an error.
An exception to this size requirement is the ifnstiff table. This table is the size of the other profiles squared. If the other f-tables are size 128, then ifnstiff should be of size 16384 (or 128 * 128). To discuss what this table does, I must first introduce the concept of a scanned matrix.
THE SCANNED MATRIX
The scanned matrix is a convention designed to describe the shape of the connections of masses(n.) in the mass(n.) and spring model.
Going back to our discussion on Newton's mechanical model, the mass(n.) and spring model describes the behavior of a string as a finite number of masses connected by springs. As you can imagine, the masses are connected sequentially, one to another, like beads on a string. Mass(n.) #1 is connected to #2, #2 connected to #3 and so on. However, the pioneers of scanned synthesis had the idea to connect the masses in a non-linear way. It's hard to imagine, because as musicians, we have experience with piano or violin strings (one dimensional strings), but not with multi-dimensional strings. Fortunately, the computer has no problem working with this idea, and the flexibility of Newton's equation allows us to use the CPU to model mass(n.) #1 being connected with springs not only to #2 but also to #3 and any other mass(n.) in the model.
The most direct and useful implementation of this concept is to connect mass #1 to mass #2 and mass #128 -- forming a string without endpoints, a circular string, like tying our string with beads to make a necklace. The pioneers of scanned synthesis discovered that this circular string model is more useful than a conventional one-dimensional string model with endpoints. In fact, scantable uses a circular string.
The matrix is described in a simple ASCII file, imported into Csound via a GEN23 generated f-table.
f3 0 16384 -23 "string-128"
This text file must be located in the same directory as your .csd or csound will give you this error
ftable 3: error opening ASCII file
You can construct your own matrix using Stephen Yi's Scanned Matrix editor included in the Blue frontend for Csound, and as a standalone Java application Scanned Synthesis Matrix Editor.
To swap out matrices, simply type the name of a different matrix file into the double quotes, i.e.:
f3 0 16384 -23 "circularstring_2-128"Different matrices have unique effects on the behavior of the system. Some matrices can make the synth extremely loud, others extremely quiet. Experiment with using different matrices.
Now would be a good time to point out that Csound has other scanned synthesis opcodes preceded with an "x", xscans, xscanu, that use a different matrix format than the one used by scans, scanu, and Stephen Yi's Scanned Matrix Editor. The Csound Reference Manual has more information on this.
THE HAMMER
If the initial shape, an f-table specified by the ipos argument determines the shape of the initial contents in our dynamic table. If you use autocomplete in CsoundQT, the scanu opcode line highlights the first p-field of scanu as the "init" opcode. In my examples I use "ipos" to avoid p1 of scanu being syntax-highlighted. But what if we want to "reset" or "pluck" the table, perhaps with a shape of a square wave instead of a sine wave, while the instrument is playing?
With scantable, there is an easy way to to this, send a score event changing the contents of the dynamic f-table. You can do this with the Csound score by adjusting the start time of the f-events in the score.
EXAMPLE 04H04_Hammer.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr=44100
kr=4410
ksmps=10
nchnls=2
0dbfs=1
instr 1
ipos ftgen 1, 0, 128, 10, 1 ; Initial Shape, sine wave range -1 to 1;
imass ftgen 2, 0, 128, -7, 1, 128, 1 ;Masses(adj.), constant value 1
istiff ftgen 3, 0, 128, -7, 50, 64, 100, 64, 0 ;Stiffness; unipolar triangle range 0 to 100
idamp ftgen 4, 0, 128, -7, 1, 128, 1; ;Damping; constant value 1
ivel ftgen 5, 0, 128, -7, 0, 128, 0 ;Initial Velocity; constant value 0
iamp = 0.5
a1 scantable iamp, 60, ipos, imass, istiff, idamp, ivel
outs a1, a1
endin
</CsInstruments>
<CsScore>
i 1 0 14
f 1 1 128 10 1 1 1 1 1 1 1 1 1 1 1
f 1 2 128 10 1 1 0 0 0 0 0 0 0 1 1
f 1 3 128 10 1 1 1 1 1
f 1 4 128 10 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
f 1 5 128 10 1 1
f 1 6 128 13 1 1 0 0 0 -.1 0 .3 0 -.5 0 .7 0 -.9 0 1 0 -1 0
f 1 7 128 21 6 5.745
</CsScore>
</CsoundSynthesizer>
;Example by Christopher Saunders</code>
You'll get the warning
WARNING: replacing previous ftable 1 This is not a bad thing, it means this method of hammering the string is working. In fact you could use this method to explore and hammer every possible GEN routine in Csound. GEN10 (sines), GEN 21 (noise) and GEN 27 (breakpoint functions) could keep you occupied for a while.
Unipolar waves have a different sound but a loss in volume can occur. There is a way to do this with scanu, but I do not use this feature and just use these values instead.
ileft = 0. iright = 1. kpos = 0. kstrngth = 0. MORE ON PROFILES
One of the biggest challenges in understanding scanned synthesis is the concept of profiles.
Setting up the opcode scanu requires 3 profiles - Centering, Mass and Damping. The pioneers of scanned synthesis discovered early on that the resultant timbre is far more interesting if marble #1 had a different centering force than mass #64.
The farther our model gets away from a physical real-world string that we know and pluck on our guitars and pianos, the more interesting the sounds for synthesis. Therefore, instead of one mass, and damping, and centering value for all 128 of the marbles each marble can have its own conditions. How the centering, mass, and damping profiles make the system behave is up to the user to discover through experimentation (more on how to experiment safely later in this chapter).
CONTROL RATE PROFILE SCALARS
Profiles are a detailed way to control the behavior of the string, but what if we want to influence the mass or centering or damping of every marble after a note has been activated and while its playing?
Scanu gives us 4 k-rate arguments kmass, kstif, kcentr, kdamp, to scale these forces. One could scale mass to volume, or have an envelope controlling centering.
Caution! These parameters can make the scanned system unstable in ways that could make extremely loud sounds come out of your computer. It is best to experiment with small changes in range and keep your headphones off. A good place to start experimenting is with different values for kcentr while keeping kmass, kstiff, and kdamp constant. You could also scale mass and stiffness to MIDI velocity.
AUDIO INJECTION
Instead of using the hammer method to move the marbles around, we could use audio to add motion to the mass and spring model. Scanu lets us do this with a simple audio rate argument. When the Reference manual says "amplitude should not be too great" it means it.
A good place to start is by scaling down the audio in the opcode line.
ain/2000 It is always a good idea to take into account the 0dbfs statement in the header. Simply put if 0dbfs =1 and you send scans an audio signal with a value of 1, you and your immediate neighbors are in for a very loud ugly sound.
amplitude should not be too great!
To bypass audio injection all together, simply assign 0 to an a-rate variable.
ain = 0 and use this variable as the argument.
CONNECTING TO SCANS
The p-field id is an arbitrary integer label that tells the scans opcode which scanu to read. By making the value of id negative, the arbitrary numerical label becomes the number of an f-table that can be used by any other opcode in Csound, like we did with scantable earlier in this chapter.
We could then use oscil to perform a table lookup algorithm to make sound out of scanu (as long as id is negative), but scanu has a companion opcode, scans which has 1 more argument than oscil. This argument is the number of an f-table containing the scan trajectory.
SCAN TRAJECTORIES
One thing we have take for granted so far with oscil is that the wave table is read front to back. If you regard oscil as a phasor and table pair, the first index of the table is always read first and the last index is always read last as in the example below:
EXAMPLE 04H05_Scan_trajectories.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr=44100 kr=4410 ksmps=10 nchnls=2 0dbfs=1 instr 1 andx phasor 440 a1 table andx*8192, 1 outs a1*.2, a1*.2 endin </CsInstruments> <CsScore> f1 0 8192 10 1 i 1 0 4 </CsScore> </CsoundSynthesizer> ;Example by Christopher Saunders
But what if we wanted to read the table indices back to front, or even "out of order"? Well we could do something like this:
EXAMPLE 04H06_Scan_trajectories2.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> sr=44100 kr=4410 ksmps=10 nchnls=2 ; STEREO 0dbfs=1 instr 1 andx phasor 440 andx table andx*8192, 1 ; read the table out of order! a1 table andx*8192, 1 outs a1*.2, a1*.2 endin </CsInstruments> <CsScore> f1 0 8192 10 1 f2 0 8192 -5 .001 8192 1; i 1 0 4 </CsScore> </CsoundSynthesizer> ;Example by Christopher Saunders
We are still dealing with 2-dimensional arrays, or f-tables as we know them. But if we remember back to our conversation about the scanned matrix, matrices are multi-dimensional, it would be a shame to only read them in "2D".
The opcode scans gives us the flexibility of specifying a scan trajectory, analogous to telling the phasor/table combination to read values non-consecutively. We could read these values, not left to right, but in a spiral order, by specifying a table to be the ifntraj argument of scans.
a3 scans iamp, kpch, ifntraj ,id , interp An f-table for the spiral method can generated by reading the ASCII file "spiral-8,16,128,2,1over2" by GEN23
f2 0 128 -23 "spiral-8,16,128,2,1over2"
The following .csd requires that the files "circularstring-128" and "spiral-8,16, 128,2,1over2" be located in the same directory as the .csd.
EXAMPLE 04H07_Scan_matrices.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> nchnls = 2 sr = 44100 ksmps = 10 0dbfs = 1 instr 1 ipos ftgen 1, 0, 128, 10, 1 irate = .005 ifnvel ftgen 6, 0, 128, -7, 0, 128, 0 ifnmass ftgen 2, 0, 128, -7, 1, 128, 1 ifnstif ftgen 3, 0, 16384,-23,"circularstring-128" ifncentr ftgen 4, 0, 128, -7, 0, 128, 2 ifndamp ftgen 5, 0, 128, -7, 1, 128, 1 imass = 2 istif = 1.1 icentr = .1 idamp = -0.01 ileft = 0. iright = .5 ipos = 0. istrngth = 0. ain = 0 idisp = 0 id = 8 scanu 1, irate, ifnvel, ifnmass, ifnstif, ifncentr, ifndamp, imass, istif, icentr, idamp, ileft, iright, ipos, istrngth, ain, idisp, id scanu 1,.007,6,2,3,4,5, 2, 1.10 ,.10 ,0 ,.1 ,.5, 0, 0,ain,1,2; iamp = .2 ifreq = 200 a1 scans iamp, ifreq, 7, id a1 dcblock a1 outs a1, a1 endin </CsInstruments> <CsScore> f7 0 128 -7 0 128 128 i 1 0 5 f7 5 128 -23 "spiral-8,16,128,2,1over2" i 1 5 5 f7 10 128 -7 127 64 1 63 127 i 1 10 5 </CsScore> </CsoundSynthesizer> ;Example by Christopher Saunders
Notice that the scan trajectory has an FM-like effect on the sound.
TABLE SIZE AND INTERPOLATION
Tables used for scan trajectory must be the same size (have the same number of indices) as the mass, centering and damping tables and must also have the same range as the size of these tables. For example, in our .csd we've been using 128 point tables for initial position, mass centering, damping (our stiffness tables have 128 squared). So our trajectory tables must be of size 128, and contain values from 0 to 127.
One can use larger or smaller tables, but their sizes must agree in this way or Csound will give you an error. Larger tables, of course significantly increase CPU usage and slow down real-time performance.
If all the sizes are multiples of a number (128), we can use Csound's Macro language extension to define the table size as a macro, and then change the definition twice (once for the orc and once for the score) instead of 10 times.
EXAMPLE 04H08_Scan_tablesize.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> nchnls = 2 sr = 44100 ksmps = 10 0dbfs = 1 #define SIZE #128# instr 1 ipos ftgen 1, 0, $SIZE., 10, 1 irate = .005 ifnvel ftgen 6, 0, $SIZE., -7, 0, $SIZE., 0 ifnmass ftgen 2, 0, $SIZE., -7, 1, $SIZE., 1 ifnstif ftgen 3, 0, $SIZE.*$SIZE.,-23, "circularstring-$SIZE." ifncentr ftgen 4, 0, $SIZE., -7, 0, $SIZE., 2 ifndamp ftgen 5, 0, $SIZE., -7, 1, $SIZE., 1 imass = 2 istif = 1.1 icentr = .1 idamp = -0.01 ileft = 0. iright = .5 ipos = 0. istrngth = 0. ain = 0 idisp = 0 id = 8 scanu 1, irate, ifnvel, ifnmass, ifnstif, ifncentr, ifndamp, imass, istif, icentr, idamp, ileft, iright, ipos, istrngth, ain, idisp, id scanu 1,.007,6,2,3,4,5, 2, 1.10 ,.10 ,0 ,.1 ,.5, 0, 0,ain,1,2; iamp = .2 ifreq = 200 a1 scans iamp, ifreq, 7, id, 4 a1 dcblock a1 outs a1, a1 endin </CsInstruments> <CsScore> #define SIZE #128# f7 0 $SIZE. -7 0 $SIZE. $SIZE. i 1 0 5 f7 5 $SIZE. -7 0 63 [$SIZE.-1] 63 0 i 1 5 5 f7 10 $SIZE. -7 [$SIZE.-1] 64 1 63 [$SIZE.-1] i 1 10 5 </CsScore> </CsoundSynthesizer> ;Example by Christopher Saunders
Macros even work in our string literal in our GEN 23 f-table! But if you define size as 64 and there isn't a file in your directory named "circularstring-64" Csound will not run your score and give you an error. Here is a link to download power-of-two size ASCII files that create circular matrices for use in this way, and of course, you can design your own stiffness matrix files with Steven Yi's scanned matrix editor.
When using smaller size tables it may be necessary to use interpolation to avoid the artifacts of a small table. scans gives us this option as a fifth optional argument, iorder, detailed in the reference manual and worth experimenting with.
Using the opcodes scanu and scans require that we fill in 22 arguments and create at least 7 f-tables, including at least one external ASCII file (because no one wants to fill in 16,384 arguments to an f-statement). This a very challenging pair of opcodes. The beauty of scanned synthesis is that there is no scanned synthesis "sound".
USING BALANCE TO TAME AMPLITUDES
However, like this frontier can be a lawless, dangerous place. When experimenting with scanned synthesis parameters, one can illicit extraordinarily loud sounds out of Csound, often by something as simple as a misplaced decimal point.
Warning: the following .csd is hot, it produces massively loud amplitude values. Be very cautious about rendering this .csd, I highly recommend rendering to a file instead of real-time.
EXAMPLE 04H09_Scan_extreme_amplitude.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> nchnls = 2 sr = 44100 ksmps = 256 0dbfs = 1 ;NOTE THIS CSD WILL NOT RUN UNLESS ;IT IS IN THE SAME FOLDER AS THE FILE "STRING-128" instr 1 ipos ftgen 1, 0, 128 , 10, 1 irate = .007 ifnvel ftgen 6, 0, 128 , -7, 0, 128, 0.1 ifnmass ftgen 2, 0, 128 , -7, 1, 128, 1 ifnstif ftgen 3, 0, 16384, -23, "string-128" ifncentr ftgen 4, 0, 128 , -7, 1, 128, 2 ifndamp ftgen 5, 0, 128 , -7, 1, 128, 1 kmass = 1 kstif = 0.1 kcentr = .01 kdamp = 1 ileft = 0 iright = 1 kpos = 0 kstrngth = 0. ain = 0 idisp = 1 id = 22 scanu ipos, irate, ifnvel, ifnmass, \ ifnstif, ifncentr, ifndamp, kmass, \ kstif, kcentr, kdamp, ileft, iright,\ kpos, kstrngth, ain, idisp, id kamp = 0dbfs*.2 kfreq = 200 ifn ftgen 7, 0, 128, -5, .001, 128, 128. a1 scans kamp, kfreq, ifn, id a1 dcblock2 a1 iatt = .005 idec = 1 islev = 1 irel = 2 aenv adsr iatt, idec, islev, irel ;outs a1*aenv,a1*aenv; Uncomment for speaker destruction; endin </CsInstruments> <CsScore> f8 0 8192 10 1; i 1 0 5 </CsScore> </CsoundSynthesizer> ;Example by Christopher Saunders
The extreme volume of this .csd comes from a value given to scanu
kdamp = .1
.1 is not exactly a safe value for this argument, in fact, any value above 0 for this argument can cause chaos.
It would take a skilled mathematician to map out safe possible ranges for all the arguments of scanu. I figured out these values through a mix of trial and error and studying other .csd
We can use the opcode balance to listen to sine wave (a signal with consistent, safe amplitude) and squash down our extremely loud scanned synth output (which is loud only because of our intentional carelessness.)
EXAMPLE 04H10_Scan_balanced_amplitudes.csd
<CsoundSynthesizer> <CsOptions> -o dac </CsOptions> <CsInstruments> nchnls = 2 sr = 44100 ksmps = 256 0dbfs = 1 ;NOTE THIS CSD WILL NOT RUN UNLESS ;IT IS IN THE SAME FOLDER AS THE FILE "STRING-128" instr 1 ipos ftgen 1, 0, 128 , 10, 1 irate = .007 ifnvel ftgen 6, 0, 128 , -7, 0, 128, 0.1 ifnmass ftgen 2, 0, 128 , -7, 1, 128, 1 ifnstif ftgen 3, 0, 16384, -23, "string-128" ifncentr ftgen 4, 0, 128 , -7, 1, 128, 2 ifndamp ftgen 5, 0, 128 , -7, 1, 128, 1 kmass = 1 kstif = 0.1 kcentr = .01 kdamp = -0.01 ileft = 0 iright = 1 kpos = 0 kstrngth = 0. ain = 0 idisp = 1 id = 22 scanu ipos, irate, ifnvel, ifnmass, \ ifnstif, ifncentr, ifndamp, kmass, \ kstif, kcentr, kdamp, ileft, iright,\ kpos, kstrngth, ain, idisp, id kamp = 0dbfs*.2 kfreq = 200 ifn ftgen 7, 0, 128, -5, .001, 128, 128. a1 scans kamp, kfreq, ifn, id a1 dcblock2 a1 ifnsine ftgen 8, 0, 8192, 10, 1 a2 oscil kamp, kfreq, ifnsine a1 balance a1, a2 iatt = .005 idec = 1 islev = 1 irel = 2 aenv adsr iatt, idec, islev, irel outs a1*aenv,a1*aenv endin </CsInstruments> <CsScore> f8 0 8192 10 1; i 1 0 5 </CsScore> </CsoundSynthesizer> ;Example by Christopher Saunders
It must be emphasized that this is merely a safeguard. We still get samples out of range when we run this .csd, but many less than if we had not used balance. It is recommended to use balance if you are doing real-time mapping of k-rate profile scalar arguments for scans; mass stiffness, damping, and centering.
REFERENCES AND FURTHER READING
Max Matthews, Bill Verplank, Rob Shaw, Paris Smaragdis, Richard Boulanger, John ffitch, Matthew Gilliard, Matt Ingalls, and Steven Yi all worked to make scanned synthesis usable, stable and openly available to the open-source Csound community. Their contributions are in the reference manual, several academic papers on scanned synthesis and journal articles, and the software that supports the Csound community.
- Csounds.com page on Scanned Synthesis
- Dr. Richard Boulanger's tutorial on Scanned Synthesis
- Steven Yi's Page on experimenting with Scanned Synthesis
05 SOUND MODIFICATION
ENVELOPES
Envelopes are used to define how a value evolves over time. In early synthesisers, envelopes were used to define the changes in amplitude in a sound across its duration thereby imbuing sounds characteristics such as 'percussive', or 'sustaining'. Envelopes are also commonly used to modulate filter cutoff frequencies and the frequencies of oscillators but in reality we are only limited by our imaginations in regard to what they can be used for.
Csound offers a wide array of opcodes for generating envelopes including ones which emulate the classic ADSR (attack-decay-sustain-release) envelopes found on hardware and commercial software synthesizers. A selection of these opcodes types shall be introduced here.
The simplest opcode for defining an envelope is line. line describes a single envelope segment as a straight line between a start value and an end value which has a given duration.
ares line ia, idur, ib kres line ia, idur, ib
In the following example line is used to create a simple envelope which is then used as the amplitude control of a poscil oscillator. This envelope starts with a value of 0.5 then over the course of 2 seconds descends in linear fashion to zero.
EXAMPLE 05A01_line.csd
<CsoundSynthesizer> <CsOptions> -odac ; activates real time sound output </CsOptions> <CsInstruments> sr = 44100 ksmps = 32 nchnls = 1 0dbfs = 1 giSine ftgen 0, 0, 2^12, 10, 1 ; a sine wave instr 1 aEnv line 0.5, 2, 0 ; amplitude envelope aSig poscil aEnv, 500, giSine ; audio oscillator out aSig ; audio sent to output endin </CsInstruments> <CsScore> i 1 0 2 ; instrument 1 plays a note for 2 seconds e </CsScore> </CsoundSynthesizer>
The envelope in the above example assumes that all notes played by this instrument will be 2 seconds long. In practice it is often beneficial to relate the duration of the envelope to the duration of the note (p3) in some way. In the next example the duration of the envelope is replaced with the value of p3 retrieved from the score, whatever that may be. The envelope will be stretched or contracted accordingly.
EXAMPLE 05A02_line_p3.csd
<CsoundSynthesizer> <CsOptions> -odac ;activates real time sound output </CsOptions> <CsInstruments> sr = 44100 ksmps = 32 nchnls = 1 0dbfs = 1 giSine ftgen 0, 0, 2^12, 10, 1 ; a sine wave instr 1 ; A single segment envelope. Time value defined by note duration. aEnv line 0.5, p3, 0 aSig poscil aEnv, 500, giSine ; an audio oscillator out aSig ; audio sent to output endin </CsInstruments> <CsScore> ; p1 p2 p3 i 1 0 1 i 1 2 0.2 i 1 3 4 e </CsScore> </CsoundSynthesizer>
It may not be disastrous if a envelope's duration does not match p3 and indeed there are many occasions when we want an envelope duration to be independent of p3 but we need to remain aware that if p3 is shorter than an envelope's duration then that envelope will be truncated before it is allowed to complete and if p3 is longer than an envelope's duration then the envelope will complete before the note ends (the consequences of this latter situation will be looked at in more detail later on in this section).
line (and most of Csound's envelope generators) can output either k or a-rate variables. k-rate envelopes are computationally cheaper than a-rate envelopes but in envelopes with fast moving segments quantisation can occur if they output a k-rate variable, particularly when the control rate is low, which in the case of amplitude envelopes can lead to clicking artefacts or distortion.
linseg is an elaboration of line and allows us to add an arbitrary number of segments by adding further pairs of time durations followed envelope values. Provided we always end with a value and not a duration we can make this envelope as long as we like.
In the next example a more complex amplitude envelope is employed by using the linseg opcode. This envelope is also note duration (p3) dependent but in a more elaborate way. An attack-decay stage is defined using explicitly declared time durations. A release stage is also defined with an explicitly declared duration. The sustain stage is the p3 dependent stage but to ensure that the duration of the entire envelope still adds up to p3, the explicitly defined durations of the attack, decay and release stages are subtracted from the p3 dependent sustain stage duration. For this envelope to function correctly it is important that p3 is not less than the sum of all explicitly defined envelope segment durations. If necessary, additional code could be employed to circumvent this from happening.
EXAMPLE 05A03_linseg.csd
<CsoundSynthesizer> <CsOptions> -odac ; activates real time sound output </CsOptions> <CsInstruments> sr = 44100 ksmps = 32 nchnls = 1 0dbfs = 1 giSine ftgen 0, 0, 2^12, 10, 1 ; a sine wave instr 1 ; a more complex amplitude envelope: ; |-attack-|-decay--|---sustain---|-release-| aEnv linseg 0, 0.01, 1, 0.1, 0.1, p3-0.21, 0.1, 0.1, 0 aSig poscil aEnv, 500, giSine out aSig endin </CsInstruments> <CsScore> i 1 0 1 i 1 2 5 e </CsScore> </CsoundSynthesizer>
The next example illustrates an approach that can be taken whenever it is required that more than one envelope segment duration be p3 dependent. This time each segment is a fraction of p3. The sum of all segments still adds up to p3 so the envelope will complete across the duration of each note regardless of duration.
EXAMPLE 05A04_linseg_p3_fractions.csd
<CsoundSynthesizer>
<CsOptions>
-odac ;activates real time sound output
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giSine ftgen 0, 0, 2^12, 10, 1 ; a sine wave
instr 1
aEnv linseg 0, p3*0.5, 1, p3*0.5, 0 ; rising then falling envelope
aSig poscil aEnv, 500, giSine
out aSig
endin
</CsInstruments>
<CsScore>
; 3 notes of different durations are played
i 1 0 1
i 1 2 0.1
i 1 3 5
e
</CsScore>
</CsoundSynthesizer>
The next example highlights an important difference in the behaviours of line and linseg when p3 exceeds the duration of an envelope.
When a note continues beyond the end of the final value of a linseg defined envelope the final value of that envelope is held. A line defined envelope behaves differently in that instead of holding its final value it continues in the trajectory defined by its one and only segment.
This difference is illustrated in the following example. The linseg and line envelopes of instruments 1 and 2 appear to be the same but the difference in their behaviour as described above when they continue beyond the end of their final segment is clear when listening to the example.
EXAMPLE 05A05_line_vs_linseg.csd
<CsoundSynthesizer> <CsOptions> -odac ; activates real time sound output </CsOptions> <CsInstruments> sr = 44100 ksmps = 32 nchnls = 1 0dbfs = 1 giSine ftgen 0, 0, 2^12, 10, 1 ; a sine wave instr 1 ; linseg envelope aCps linseg 300, 1, 600 ; linseg holds its last value aSig poscil 0.2, aCps, giSine out aSig endin instr 2 ; line envelope aCps line 300, 1, 600 ; line continues its trajectory aSig poscil 0.2, aCps, giSine out aSig endin </CsInstruments> <CsScore> i 1 0 5 ; linseg envelope i 2 6 5 ; line envelope e </CsScore> </CsoundSynthesizer>
expon and expseg are versions of line and linseg that instead produce envelope segments with concave exponential shapes rather than linear shapes. expon and expseg can often be more musically useful for envelopes that define amplitude or frequency as they will reflect the logarithmic nature of how these parameters are perceived. On account of the mathematics that are used to define these curves, we cannot define a value of zero at any node in the envelope and an envelope cannot cross the zero axis. If we require a value of zero we can instead provide a value very close to zero. If we still really need zero we can always subtract the offset value from the entire envelope in a subsequent line of code.
The following example illustrates the difference between line and expon when applied as amplitude envelopes.
EXAMPLE 05A06_line_vs_expon.csd
<CsoundSynthesizer> <CsOptions> -odac ; activates real time sound output </CsOptions> <CsInstruments> sr = 44100 ksmps = 32 nchnls = 1 0dbfs = 1 giSine ftgen 0, 0, 2^12, 10, 1 ; a sine wave instr 1 ; line envelope aEnv line 1, p3, 0 aSig poscil aEnv, 500, giSine out aSig endin instr 2 ; expon envelope aEnv expon 1, p3, 0.0001 aSig poscil aEnv, 500, giSine out aSig endin </CsInstruments> <CsScore> i 1 0 2 ; line envelope i 2 2 1 ; expon envelope e </CsScore> </CsoundSynthesizer>
The nearer our 'near-zero' values are to zero the quicker the curve will appear to reach 'zero'. In the next example smaller and smaller envelope end values are passed to the expon opcode using p4 values in the score. The percussive 'ping' sounds are perceived to be increasingly short.
EXAMPLE 05A07_expon_pings.csd
<CsoundSynthesizer>
<CsOptions>
-odac ; activates real time sound output
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giSine ftgen 0, 0, 2^12, 10, 1 ; a sine wave
instr 1; expon envelope
iEndVal = p4 ; variable 'iEndVal' retrieved from score
aEnv expon 1, p3, iEndVal
aSig poscil aEnv, 500, giSine
out aSig
endin
</CsInstruments>
<CsScore>
;p1 p2 p3 p4
i 1 0 1 0.001
i 1 1 1 0.000001
i 1 2 1 0.000000000000001
e
</CsScore>
</CsoundSynthesizer>
Note that expseg does not behave like linseg in that it will not hold its last final value if p3 exceeds its entire duration, instead it continues its curving trajectory in a manner similar to line (and expon). This could have dangerous results if used as an amplitude envelope.
When dealing with notes with an indefinite duration at the time of initiation (such as midi activated notes or score activated notes with a negative p3 value), we do not have the option of using p3 in a meaningful way. Instead we can use one of Csound's envelopes that sense the ending of a note when it arrives and adjust their behaviour according to this. The opcodes in question are linenr, linsegr, expsegr, madsr, mxadsr and envlpxr. These opcodes wait until a held note is turned off before executing their final envelope segment. To facilitate this mechanism they extend the duration of the note so that this final envelope segment can complete.
The following example uses midi input (either hardware or virtual) to activate notes. The use of the linsegr envelope means that after the short attack stage lasting 0.1 seconds, the penultimate value of 1 will be held as long as the note is sustained but as soon as the note is released the note will be extended by 0.5 seconds in order to allow the final envelope segment to decay to zero.
EXAMPLE 05A08_linsegr.csd
<CsoundSynthesizer>
<CsOptions>
-odac -+rtmidi=virtual -M0
; activate real time audio and MIDI (virtual midi device)
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giSine ftgen 0, 0, 2^12, 10, 1 ; a sine wave
instr 1
icps cpsmidi
; attack-|sustain-|-release
aEnv linsegr 0, 0.01, 0.1, 0.5,0 ; envelope that senses note releases
aSig poscil aEnv, icps, giSine ; audio oscillator
out aSig ; audio sent to output
endin
</CsInstruments>
<CsScore>
f 0 240 ; csound performance for 4 minutes
e
</CsScore>
</CsoundSynthesizer>
Sometimes designing our envelope shape in a function table can provide us with shapes that are not possible using Csound's envelope generating opcodes. In this case the envelope can be read from the function table using an oscillator. If the oscillator is given a frequency of 1/p3 then it will read though the envelope just once across the duration of the note.
The following example generates an amplitude envelope which uses the shape of the first half of a sine wave.
EXAMPLE 05A09_sine_env.csd
<CsoundSynthesizer>
<CsOptions>
-odac ; activate real time sound output
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giSine ftgen 0, 0, 2^12, 10, 1 ; a sine wave
giEnv ftgen 0, 0, 2^12, 9, 0.5, 1, 0 ; envelope shape: a half sine
instr 1
; read the envelope once during the note's duration:
aEnv poscil 1, 1/p3, giEnv
aSig poscil aEnv, 500, giSine ; audio oscillator
out aSig ; audio sent to output
endin
</CsInstruments>
<CsScore>
; 7 notes, increasingly short
i 1 0 2
i 1 2 1
i 1 3 0.5
i 1 4 0.25
i 1 5 0.125
i 1 6 0.0625
i 1 7 0.03125
f 0 7.1
e
</CsScore>
</CsoundSynthesizer>
Comparison of the Standard Envelope Opcodes
The precise shape of the envelope of a sound, whether that envelope refers to its amplitude, its pitch or any other parameter, can be incredibly subtle and our ears, in identifying and characterising sounds, are fantastically adept at sensing those subtleties. Csound's original envelope generating opcode linseg, whilst capable of emulating the envelope generators of vintage electronic synthesisers, may not produce convincing results in the emulation of acoustic instruments and natural sound. linseg has, since Csound's creation, been augmented with a number of other envelope generators whose usage is similar to that of linseg but whose output function is subtly different in shape.
If we consider a basic envelope that ramps up across ¼ of the duration of a note, then sustains for ½ the durations of the and finally ramps down across the remaining ¼ duration of the note, we can implement this envelope using linseg thus:
kEnv linseg 0, p3/4, 0.9, p3/2, 0.9, p3/4, 0
The resulting envelope will look like this:
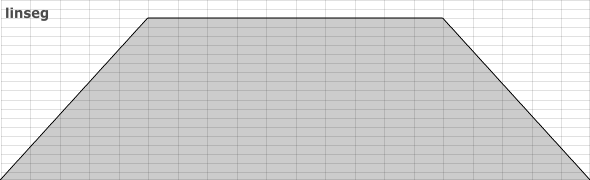
When employed as an amplitude control, the resulting sound may seem to build rather too quickly, then crescendo in a slightly mechanical fashion and finally arrive at its sustain portion with abrupt stop in the crescendo. Similar critcism could be levelled at the latter part of the envelope going from sustain to ramping down.
The expseg opcode, introduced sometime after linseg, attempted to address the issue of dynamic response when mapping an envelope to amplitude. Two caveats exist in regard to the use of expseg: firstly a single expseg definition cannot cross from the positive domain to the negative domain (and vice versa), and secondly it cannot reach zero. This second caveat means that an amplitude envelope created using expseg cannot express 'silence' unless we remove the offset away form zero that the envelope employs. An envelope with similar input values to the linseg envelope above but created with expseg could use the following code:
kEnv expseg 0.001, p3/4, 0.901, p3/2, 0.901, p3/4, 0.001
kEnv = kEnv – 0.001
and would look like this:
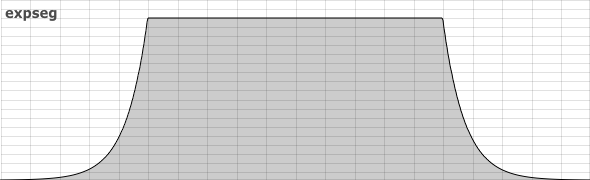
In this example the offset above zero has been removed. This time we can see that the sound will build in a rather more natural and expressive way, however the change from crescendo to sustain is even more abrupt this time. Adding some lowpass filtering to the envelope signal can smooth these abrupt changes in direction. This could be done with, for example, the port opcode given a half-point value of 0.05.
kEnv port kEnv, 0.05
The resulting envelope looks like this:
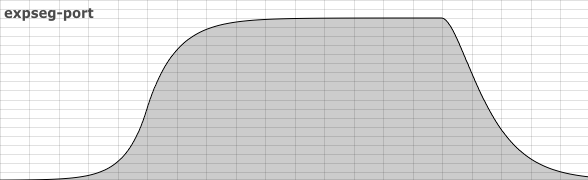
The changes to and from the sustain portion have clearly been improved but close examination of the end of the envelope reveals that the use of port has prevented the envelope from reaching zero. Extending the duration of the note or overlaying a second 'anti-click' envelope should obviate this issue.
xtratim 0.1
will extend the note by 1/10 of a second.
aRamp linseg 1, p3-0.1, 1, 0.1, 0
will provide a quick ramp down at the note conclusion if multiplied to the previously created envelope.
A more recently introduced alternative is the cosseg opcode which applies a cosine transfer function to each segment of the envelope. Using the following code:
kEnv cosseg 0, p3/4, 0.9, p3/2, 0.9, p3/4, 0
the resulting envelope will look like this:
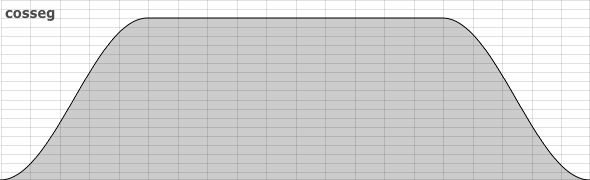
t can be observed that this envelope provides a smooth gradual building up from silence and and a gradual arrival at the sustain level. This opcodes has no restrictions relating to changing polarity or passing through zero.
Another alternative that offers enhanced user control and that might in many situations provide more natural results is the transeg opcode. transeg allows us to specify the curvature of each segment but it should be noted that the curvature is dependent upon whether the segment is rising or falling. For example a positive curvature will result in a concave segment in a rising segment but a convex segment in a falling segment. The following code:
kEnv transeg 0, p3/4, -4, 0.9, p3/2, 0, 0.9, p3/4, -4, 0
will produce the following envelope:
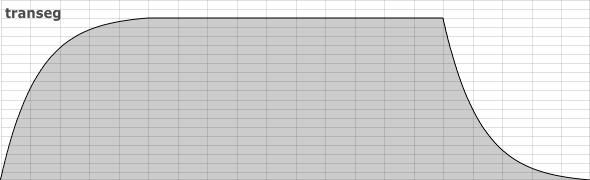
This looks perhaps rather lopsided but in emulating acoustic instruments can actually produce more natural results. Considering an instrument such as a clarinet, it is in reality very difficult to fade a note in smoothly from silence. It is more likely that a note will 'start' slightly abruptly in spite of the player's efforts. This aspect is well represented by the attack portion of the envelope above. When the note is stopped, its amplitude will decay quickly and exponentially as reflected in the envelope also. Similar attack and release characteristics can be observed in the slight pitch envelopes expressed by wind instruments.
lpshold, loopseg and looptseg - A Csound TB303
The next example introduces three of Csound's looping opcodes, lpshold, loopseg and looptseg.
These opcodes generate envelopes which are looped at a rate corresponding to a defined frequency. What they each do could also be accomplished using the 'envelope from table' technique outlined in an earlier example but these opcodes provide the added convenience of encapsulating all the required code in one line without the need for phasors, tables and ftgens. Furthermore all of the input arguments for these opcodes can be modulated at k-rate.
lpshold generates an envelope in which each break point is held constant until a new break point is encountered. The resulting envelope will contain horizontal line segments. In our example this opcode will be used to generate the notes (as MIDI note numbers) for a looping bassline in the fashion of a Roland TB303. Because the duration of the entire envelope is wholly dependent upon the frequency with which the envelope repeats - in fact it is the reciprocal of the frequency – values for the durations of individual envelope segments are not defining times in seconds but instead represent proportions of the entire envelope duration. The values given for all these segments do not need to add up to any specific value as Csound rescales the proportionality according to the sum of all segment durations. You might find it convenient to contrive to have them all add up to 1, or to 100 – either is equally valid. The other looping envelope opcodes discussed here use the same method for defining segment durations.
loopseg allows us to define a looping envelope with linear segments. In this example it is used to define the amplitude envelope for each individual note. Take note that whereas the lpshold envelope used to define the pitches of the melody repeats once per phrase, the amplitude envelope repeats once for each note of the melody, therefore its frequency is 16 times that of the melody envelope (there are 16 notes in our melodic phrase).
looptseg is an elaboration of loopseg in that is allows us to define the shape of each segment individually, whether that be convex, linear or concave. This aspect is defined using the 'type' parameters. A 'type' value of 0 denotes a linear segement, a positive value denotes a convex segment with higher positive values resulting in increasingly convex curves. Negative values denote concave segments with increasing negative values resulting in increasingly concave curves. In this example looptseg is used to define a filter envelope which, like the amplitude envelope, repeats for every note. The addition of the 'type' parameter allows us to modulate the sharpness of the decay of the filter envelope. This is a crucial element of the TB303 design.
Other crucial features of this instrument, such as 'note on/off' and 'hold' for each step, are also implemented using lpshold.
A number of the input parameters of this example are modulated automatically using the randomi opcodes in order to keep it interesting. It is suggested that these modulations could be replaced by linkages to other controls such as CsoundQt widgets, FLTK widgets or MIDI controllers. Suggested ranges for each of these values are given in the .csd.
EXAMPLE 05A10_lpshold_loopseg.csd
<CsoundSynthesizer>
<CsOptions>
-odac ;activates real time sound output
</CsOptions>
<CsInstruments>
; Example by Iain McCurdy
sr = 44100
ksmps = 4
nchnls = 1
0dbfs = 1
seed 0; seed random number generators from system clock
instr 1; Bassline instrument
kTempo = 90 ; tempo in beats per minute
kCfBase randomi 1,4, 0.2 ; base filter frequency (oct format)
kCfEnv randomi 0,4,0.2 ; filter envelope depth
kRes randomi 0.5,0.9,0.2 ; filter resonance
kVol = 0.5 ; volume control
kDecay randomi -10,10,0.2 ; decay shape of the filter.
kWaveform = 0 ; oscillator waveform. 0=sawtooth 2=square
kDist randomi 0,1,0.1 ; amount of distortion
kPhFreq = kTempo/240 ; freq. to repeat the entire phrase
kBtFreq = (kTempo)/15 ; frequency of each 1/16th note
; -- Envelopes with held segments --
; The first value of each pair defines the relative duration of that segment,
; the second, the value itself.
; Note numbers (kNum) are defined as MIDI note numbers.
; Note On/Off (kOn) and hold (kHold) are defined as on/off switches, 1 or zero
; note:1 2 3 4 5 6 7 8
; 9 10 11 12 13 14 15 16 0
kNum lpshold kPhFreq, 0, 0,40, 1,42, 1,50, 1,49, 1,60, 1,54, 1,39, 1,40, \
1,46, 1,36, 1,40, 1,46, 1,50, 1,56, 1,44, 1,47,1
kOn lpshold kPhFreq, 0, 0,1, 1,1, 1,1, 1,1, 1,1, 1,1, 1,0, 1,1, \
1,1, 1,1, 1,1, 1,1, 1,1, 1,1, 1,0, 1,1, 1
kHold lpshold kPhFreq, 0, 0,0, 1,1, 1,1, 1,0, 1,0, 1,0, 1,0, 1,1, \
1,0, 1,0, 1,1, 1,1, 1,1, 1,1, 1,0, 1,0, 1
kHold vdel_k kHold, 1/kBtFreq, 1 ; offset hold by 1/2 note duration
kNum portk kNum, (0.01*kHold) ; apply portamento to pitch changes
; if note is not held: no portamento
kCps = cpsmidinn(kNum) ; convert note number to cps
kOct = octcps(kCps) ; convert cps to oct format
; amplitude envelope attack sustain decay gap
kAmpEnv loopseg kBtFreq, 0, 0, 0,0.1, 1, 55/kTempo, 1, 0.1,0, 5/kTempo,0,0
kAmpEnv = (kHold=0?kAmpEnv:1) ; if a held note, ignore envelope
kAmpEnv port kAmpEnv,0.001
; filter envelope
kCfOct looptseg kBtFreq,0,0,kCfBase+kCfEnv+kOct,kDecay,1,kCfBase+kOct
; if hold is off, use filter envelope, otherwise use steady state value:
kCfOct = (kHold=0?kCfOct:kCfBase+kOct)
kCfOct limit kCfOct, 4, 14 ; limit the cutoff frequency (oct format)
aSig vco2 0.4, kCps, i(kWaveform)*2, 0.5 ; VCO-style oscillator
aFilt lpf18 aSig, cpsoct(kCfOct), kRes, (kDist^2)*10 ; filter audio
aSig balance aFilt,aSig ; balance levels
kOn port kOn, 0.006 ; smooth on/off switching
; audio sent to output, apply amp. envelope,
; volume control and note On/Off status
aAmpEnv interp kAmpEnv*kOn*kVol
out aSig * aAmpEnv
endin
</CsInstruments>
<CsScore>
i 1 0 3600 ; instr 1 plays for 1 hour
e
</CsScore>
</CsoundSynthesizer>
Hopefully this final example has provided some idea as to the extend of parameters that can be controlled using envelopes and also an allusion to their importance in the generation of musical 'gesture'.
PANNING AND SPATIALIZATION
Simple Stereo Panning
Csound provides a large number of opcodes designed to assist in the distribution of sound amongst two or more speakers. These range from opcodes that merely balance a sound between two channels to one that include algorithms to simulate the doppler shift which occurs when sound moves, algorithms that simulate the filtering and inter-aural delay that occurs as sound reaches both our ears and algorithms that simulate distance in an acoustic space.
First we will look at some methods of panning a sound between two speakers based on first principles.
The simplest method that is typically encountered is to multiply one channel of audio (aSig) by a panning variable (kPan) and to multiply the other side by 1 minus the same variable like this:
aSigL = aSig * kPan
aSigR = aSig * (1 – kPan)
outs aSigL, aSigR
kPan should be a value within the range zero and 1. If kPan is 1 all of the signal will be in the left channel, if it is zero, all of the signal will be in the right channel and if it is 0.5 there will be signal of equal amplitude in both the left and the right channels. This way the signal can be continuously panned between the left and right channels.
The problem with this method is that the overall power drops as the sound is panned to the middle.
One possible solution to this problem is to take the square root of the panning variable for each channel before multiplying it to the audio signal like this:
aSigL = aSig * sqrt(kPan)
aSigR = aSig * sqrt((1 – kPan))
outs aSigL, aSigR
By doing this, the straight line function of the input panning variable becomes a convex curve, so that less power is lost as the sound is panned centrally.
Using 90º sections of a sine wave for the mapping produces a more convex curve and a less immediate drop in power as the sound is panned away from the extremities. This can be implemented using the code shown below.
aSigL = aSig * sin(kPan*$M_PI_2)
aSigR = aSig * cos(kPan*$M_PI_2)
outs aSigL, aSigR
(Note that '$M_PI_2' is one of Csound's built in macros and is equivalent to pi/2.)
A fourth method, devised by Michael Gogins, places the point of maximum power for each channel slightly before the panning variable reaches its extremity. The result of this is that when the sound is panned dynamically it appears to move beyond the point of the speaker it is addressing. This method is an elaboration of the previous one and makes use of a different 90 degree section of a sine wave. It is implemented using the following code:
aSigL = aSig * sin((kPan + 0.5) * $M_PI_2)
aSigR = aSig * cos((kPan + 0.5) * $M_PI_2)
outs aSigL, aSigR
The following example demonstrates all three methods one after the other for comparison. Panning movement is controlled by a slow moving LFO. The input sound is filtered pink noise.
EXAMPLE 05B01_Pan_stereo.csd
<CsoundSynthesizer>
<CsOptions>
-odac ; activates real time sound output
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 10
nchnls = 2
0dbfs = 1
instr 1
imethod = p4 ; read panning method variable from score (p4)
;---------------- generate a source sound -------------------
a1 pinkish 0.3 ; pink noise
a1 reson a1, 500, 30, 1 ; bandpass filtered
aPan lfo 0.5, 1, 1 ; panning controlled by an lfo
aPan = aPan + 0.5 ; offset shifted +0.5
;------------------------------------------------------------
if imethod=1 then
;------------------------ method 1 --------------------------
aPanL = aPan
aPanR = 1 - aPan
;------------------------------------------------------------
endif
if imethod=2 then
;------------------------ method 2 --------------------------
aPanL = sqrt(aPan)
aPanR = sqrt(1 - aPan)
;------------------------------------------------------------
endif
if imethod=3 then
;------------------------ method 3 --------------------------
aPanL = sin(aPan*$M_PI_2)
aPanR = cos(aPan*$M_PI_2)
;------------------------------------------------------------
endif
if imethod=4 then
;------------------------ method 4 --------------------------
aPanL = sin((aPan + 0.5) * $M_PI_2)
aPanR = cos((aPan + 0.5) * $M_PI_2)
;------------------------------------------------------------
endif
outs a1*aPanL, a1*aPanR ; audio sent to outputs
endin
</CsInstruments>
<CsScore>
; 4 notes one after the other to demonstrate 4 different methods of panning
; p1 p2 p3 p4(method)
i 1 0 4.5 1
i 1 5 4.5 2
i 1 10 4.5 3
i 1 15 4.5 4
e
</CsScore>
</CsoundSynthesizer>
An opcode called pan2 exists which makes it slightly easier for us to implement various methods of panning. The following example demonstrates the three methods that this opcode offers one after the other. The first is the 'equal power' method, the second 'square root' and the third is simple linear. The Csound Manual describes a fourth method but this one does not seem to function currently.
EXAMPLE 05B02_pan2.csd
<CsoundSynthesizer> <CsOptions> -odac ; activates real time sound output </CsOptions> <CsInstruments> sr = 44100 ksmps = 10 nchnls = 2 0dbfs = 1 instr 1 imethod = p4 ; read panning method variable from score (p4) ;----------------------- generate a source sound ------------------------ aSig pinkish 0.5 ; pink noise aSig reson aSig, 500, 30, 1 ; bandpass filtered ;------------------------------------------------------------------------ ;---------------------------- pan the signal ---------------------------- aPan lfo 0.5, 1, 1 ; panning controlled by an lfo aPan = aPan + 0.5 ; DC shifted + 0.5 aSigL, aSigR pan2 aSig, aPan, imethod; create stereo panned output ;------------------------------------------------------------------------ outs aSigL, aSigR ; audio sent to outputs endin </CsInstruments> <CsScore> ; 3 notes one after the other to demonstrate 3 methods used by pan2 ;p1 p2 p3 p4 i 1 0 4.5 0 ; equal power (harmonic) i 1 5 4.5 1 ; square root method i 1 10 4.5 2 ; linear e </CsScore> </CsoundSynthesizer>
In the next example we will generate some sounds as the primary signal. We apply some delay and reverb to this signal to produce a secondary signal. A random function will pan the primary signal between the channels, but the secondary signal remains panned in the middle all the time.
EXAMPLE 05B03_Different_pan_layers.csd
<CsoundSynthesizer>
<CsOptions>
-o dac -d
</CsOptions>
<CsInstruments>
; Example by Bjorn Houdorf, March 2013
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
seed 0
instr 1
ktrig metro 0.8; Trigger frequency, instr. 2
scoreline "i 2 0 4", ktrig
endin
instr 2
ital random 60, 72; random notes
ifrq = cpsmidinn(ital)
knumpart1 oscili 4, 0.1, 1
knumpart2 oscili 5, 0.11, 1
; Generate primary signal.....
asig buzz 0.1, ifrq, knumpart1*knumpart2+1, 1
ipan random 0, 1; ....make random function...
asigL, asigR pan2 asig, ipan, 1; ...pan it...
outs asigL, asigR ;.... and output it..
kran1 randomi 0,4,3
kran2 randomi 0,4,3
asigdel1 delay asig, 0.1+i(kran1)
asigdel2 delay asig, 0.1+i(kran2)
; Make secondary signal...
aL, aR reverbsc asig+asigdel1, asig+asigdel2, 0.9, 15000
outs aL, aR; ...and output it
endin
</CsInstruments>
<CsScore>
f1 0 8192 10 1
i1 0 60
</CsScore>
</CsoundSynthesizer>
3D Binaural Encoding
3D binaural encoding is available through a number of opcodes that make use of spectral data files that provide information about the filtering and inter-aural delay effects of the human head. The oldest one of these is hrtfer. Newer ones are hrtfmove, hrtfmove2 and hrtfstat. The main parameters for control of the opcodes are azimuth (the horizontal direction of the source expressed as an angle formed from the direction in which we are facing) and elevation (the angle by which the sound deviates from this horizontal plane, either above or below). Both these parameters are defined in degrees. 'Binaural' infers that the stereo output of this opcode should be listened to using headphones so that no mixing in the air of the two channels occurs before they reach our ears (although a degree of effect is still audible through speakers).
The following example take a monophonic source sound of noise impulses and processes it using the hrtfmove2 opcode. First of all the sound is rotated around us in the horizontal plane then it is raised above our head then dropped below us and finally returned to be level and directly in front of us. For this example to work you will need to download the files hrtf-44100-left.dat and hrtf-44100-right.dat (a place to download them may be here) and place them in your SADIR (see setting environment variables) or in the same directory as the .csd.
EXAMPLE 05B04_hrtfmove.csd
<CsoundSynthesizer>
<CsOptions>
-odac ; activates real time sound output
</CsOptions>
<CsInstruments>
; Example by Iain McCurdy
sr = 44100
ksmps = 10
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^12, 10, 1 ; sine wave
giLFOShape ftgen 0, 0, 131072, 19, 0.5,1,180,1 ; U-shape parabola
instr 1
; create an audio signal (noise impulses)
krate oscil 30,0.2,giLFOShape ; rate of impulses
; amplitude envelope: a repeating pulse
kEnv loopseg krate+3,0, 0,1, 0.05,0, 0.95,0,0
aSig pinkish kEnv ; noise pulses
; -- apply binaural 3d processing --
; azimuth (direction in the horizontal plane)
kAz linseg 0, 8, 360
; elevation (held horizontal for 8 seconds then up, then down, then horizontal
kElev linseg 0, 8, 0, 4, 90, 8, -40, 4, 0
; apply hrtfmove2 opcode to audio source - create stereo ouput
aLeft, aRight hrtfmove2 aSig, kAz, kElev, \
"hrtf-44100-left.dat","hrtf-44100-right.dat"
outs aLeft, aRight ; audio to outputs
endin
</CsInstruments>
<CsScore>
i 1 0 24 ; instr 1 plays a note for 24 seconds
e
</CsScore>
</CsoundSynthesizer>
Going Multichannel
So far we have only considered working in 2-channels/stereo, but Csound is extremely flexible at working in more that 2 channels. By changing nchnls in the orchestra header we can specify any number of channels but we also need to ensure that we choose an audio hardware device using -odac that can handle multichannel audio. Audio channels sent from Csound, that do not address hardware channels, will simply not be reproduced. There may be some need to make adjustments to the software settings of your soundcard using its own software or the operating system's software, but due to the variety of sound hardware options available, it would be impossible to offer further specific advice here.
Sending Multichannel Sound to the Loudspeakers
In order to send multichannel audio we must use opcodes designed for that task. So far we have used outs to send stereo sound to a pair of loudspeakers. (The 's' actually stands for 'stereo'). Correspondingly there exist opcodes for quadophonic (outq), hexaphonic (outh), octophonic (outo), 16-channel sound (outx) and 32-channel sound (out32).
For example:
outq a1, a2, a3, a4
sends four independent audio streams to four hardware channels. Any unrequired channels still have to be given an audio signal. A typical workaround would be to give them 'silence'. For example if only 5 channels were required:
nchnls = 6
; --snip--
aSilence = 0
outh a1, a2, a3, a4, a5, aSilence
These opcodes only address very specific loudspeaker arrangements (although workarounds are possible) and have been superseded, to a large extent, by newer opcodes that allow greater flexibility in the number and routing of audio to a multichannel output.
outc allows us to address any number of output audio channels, but they still need to be addressed sequentially. For example our 5-channel audio could be design as follows:
nchnls = 5
; --snip--
outc a1, a2, a3, a4, a5
outch allows us to direct audio to a specific channel or list of channels and takes the form:
outch kchan1, asig1 [, kchan2] [, asig2] [...]
For example, our 5-channel audio system could be designed using outch as follows:
nchnls = 5
; --snip--
outch 1,a1, 2,a2, 3,a3, 4,a4, 5,a5
Note that channel numbers can be changed at k-rate thereby opening the possibility of changing the speaker configuration dynamically during performance. Channel numbers do not need to be sequential and unrequired channels can be left out completely. This can make life much easier when working with complex systems employing many channels.
Flexibly Moving Between Stereo and Multichannel
It may be useful to be able to move between working in multichannel (beyond stereo) and then moving back to stereo (when, for example, a multichannel setup is not available). It won't be sufficient to simply change nchnls = 2. It will also be necessary to change all outq, outo, outch etc to outs. In complex orchestras this could laboursome and particularly so if it is required to go back to a multichannel configuration later on. In this situation conditional outputs based on the nchnls value are useful. For example:
if nchnls==4 then
outq a1,a2,a3,a4
elseif nchnls==2 then
outs a1+a3, a2+a4
endif
Using this method, it will only be required to change nchnls = ... in the orchestra header. In stereo mode, if nchnls = 2, at least all audio streams will be monitored, even if the results do not reflect the four channel spatial arrangement.
Rendering Multichannel Audio Streams as Sound Files
So far we have referred to outs, outo etc. as a means to send audio to the speakers but strictly speaking they are only sending audio to Csound's output (as specified by nchnls) and the final destination will be defined using a command line flag in <CsOptions></CsOptions>. -odac will indeed instruct Csound to send audio to the audio hardware and then onto the speakers but we can alternatively send audio to a sound file using -oSoundFile.wav. Provided a file type that supports multichannel interleaved data is chosen (".wav" will work), a multichannel file will be created that can be used in some other audio applications or can be re-read by Csound later on by using, for example, diskin2. This method is useful for rendering audio that is too complex to be monitored in real-time. Only single interleaved sound files can be created, separate mono files cannot be created using this method. Simultaneously monitoring the audio generated by Csound whilst rendering will not be possible when using this method; we must choose one or the other.
An alternative method of rendering audio in Csound, and one that will allow simulatenous monitoring in real-time, is to use the fout opcode. For example:
fout "FileName.wav", 8, a1, a2, a3, a4
outq a1, a2, a3, a4
will render an interleaved, 24-bit, 4-channel sound file whilst simultaneously sending the quadrophonic audio to the loudspeakers.
If we wanted to de-interleave an interleaved sound file into multiple mono sound files we could use the code:
a1, a2, a3, a4 soundin "4ChannelSoundFile.wav" fout "Channel1.wav", 8, a1 fout "Channel2.wav", 8, a2 fout "Channel3.wav", 8, a3 fout "Channel4.wav", 8, a4
VBAP
Vector Base Amplitude Panning1 can be described as a method which extends stereo panning to more than two speakers. The number of speakers is, in general, arbitrary. You can configure for standard layouts such as quadrophonic, octophonic or 5.1 configuration, but in fact any number of speakers can be positioned even in irregular distances from each other. If you are fortunate enough to have speakers arranged at different heights, you can even configure VBAP for three dimensions.
Basic Steps
First you must tell VBAP where your loudspeakers are positioned. Let us assume you have seven speakers in the positions and numberings outlined below (M = middle/centre):
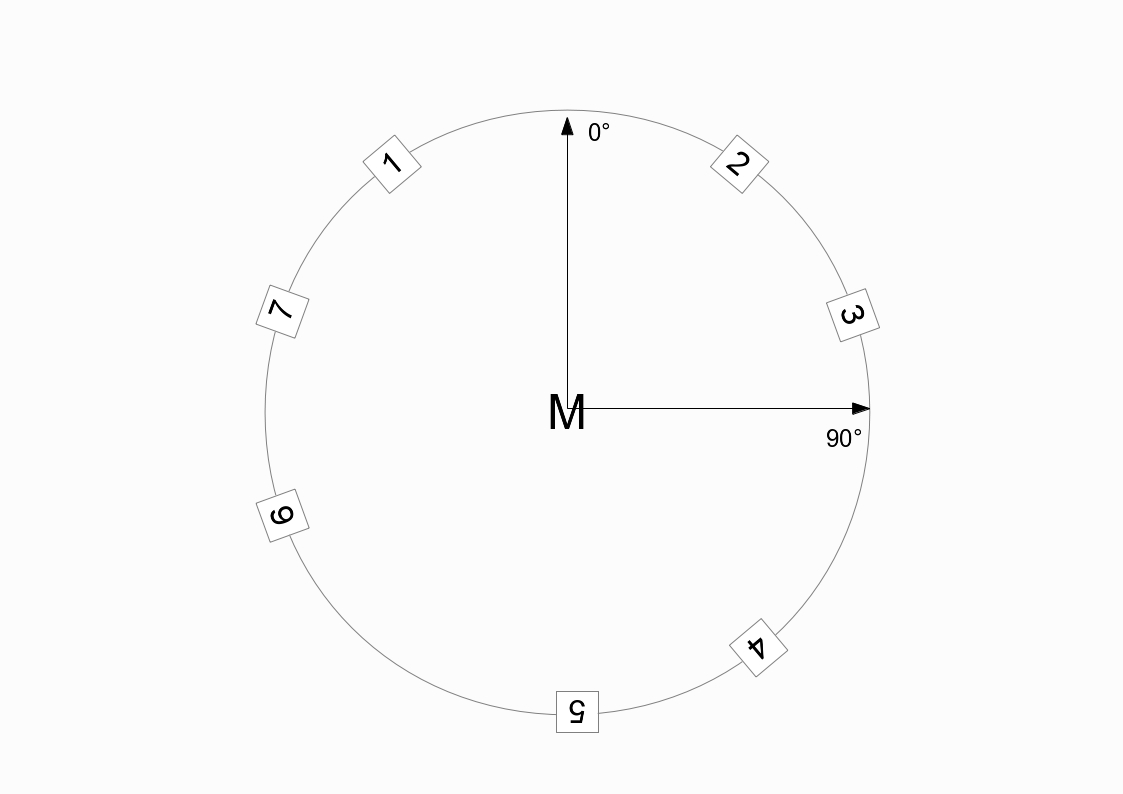
The opcode vbaplsinit, which is usually placed in the header of a Csound orchestra, defines these positions as follows:
vbaplsinit 2, 7, -40, 40, 70, 140, 180, -110, -70
The first number determines the number of dimensions (here 2). The second number states the overall number of speakers, then followed by the positions in degrees (clockwise).
All that is required now is to provide vbap with a monophonic sound source to be distributed amongst the speakers according to information given about the position. Horizontal position (azimuth) is expressed in degrees clockwise just as the initial locations of the speakers were. The following would be the Csound code to play the sound file "ClassGuit.wav" once while moving it counterclockwise:
EXAMPLE 05B05_VBAP_circle.csd
<CsoundSynthesizer> <CsOptions> -odac -d ;for the next line, change to your folder --env:SSDIR+=/home/jh/Joachim/Csound/FLOSS/audio </CsOptions> <CsInstruments> sr = 44100 ksmps = 32 0dbfs = 1 nchnls = 7 vbaplsinit 2, 7, -40, 40, 70, 140, 180, -110, -70 instr 1 Sfile = "ClassGuit.wav" iFilLen filelen Sfile p3 = iFilLen aSnd, a0 soundin Sfile kAzim line 0, p3, -360 ;counterclockwise a1, a2, a3, a4, a5, a6, a7, a8 vbap8 aSnd, kAzim outch 1, a1, 2, a2, 3, a3, 4, a4, 5, a5, 6, a6, 7, a7 endin </CsInstruments> <CsScore> i 1 0 1 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
In the CsOptions tag, you see the option --env:SSDIR+= ... as a possibility to add a folder to the path in which Csound usually looks for your samples (SSDIR = Sound Sample Directory) if you call them only by name, without the full path. To play the full length of the sound file (without prior knowledge of its duration) the filelen opcode is used to derive this duration, and then the duration of this instrument (p3) is set to this value. The p3 given in the score section (here 1) is overwritten by this value.
The circular movement is a simple k-rate line signal, from 0 to -360 across the duration of the sound file (in this case the same as p3). Note that we have to use the opcode vbap8 here, as there is no vbap7. Just give the eighth channel a variable name (a8) and thereafter ignore it.
The Spread Parameter
As VBAP derives from a panning paradigm, it has one problem which becomes more serious as the number of speakers increases. Panning between two speakers in a stereo configuration means that all speakers are active. Panning between two speakers in a quadro configuration means that half of the speakers are active. Panning between two speakers in an octo configuration means that only a quarter of the speakers are active and so on; so that the actual perceived extent of the sound source becomes unintentionally smaller and smaller.
To alleviate this tendency, Ville Pulkki has introduced an additional parameter, called 'spread', which has a range of zero to hundred percent.2 The 'ascetic' form of VBAP we have seen in the previous example, means: no spread (0%). A spread of 100% means that all speakers are active, and the information about where the sound comes from is nearly lost.
As the kspread input to the vbap8 opcode is the second of two optional parameters, we first have to provide the first one. kelev defines the elevation of the sound - it is always zero for two dimensions, as in the speaker configuration in our example. The next example adds a spread movement to the previous one. The spread starts at zero percent, then increases to hundred percent, and then decreases back down to zero.
EXAMPLE 05B06_VBAP_spread.csd
<CsoundSynthesizer> <CsOptions> -odac -d ;for the next line, change to your folder --env:SSDIR+=/home/jh/Joachim/Csound/FLOSS/audio </CsOptions> <CsInstruments> sr = 44100 ksmps = 32 0dbfs = 1 nchnls = 7 vbaplsinit 2, 7, -40, 40, 70, 140, 180, -110, -70 instr 1 Sfile = "ClassGuit.wav" iFilLen filelen Sfile p3 = iFilLen aSnd, a0 soundin Sfile kAzim line 0, p3, -360 kSpread linseg 0, p3/2, 100, p3/2, 0 a1, a2, a3, a4, a5, a6, a7, a8 vbap8 aSnd, kAzim, 0, kSpread outch 1, a1, 2, a2, 3, a3, 4, a4, 5, a5, 6, a6, 7, a7 endin </CsInstruments> <CsScore> i 1 0 1 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
New VBAP Opcodes
As a response to a number of requests, John fFitch has written new VBAP opcodes in 2012 whose main goal is to allow more than one loudspeaker configuration within a single orchestra (so that you can switch between them during performance) and to provide more flexibility in the number of output channels used. Here is an example for three different configurations which are called in three different instruments:
EXAMPLE 05B07_VBAP_new.csd
<CsoundSynthesizer>
<CsOptions>
-odac -d ;for the next line, change to your folder
--env:SSDIR+=/home/jh/Joachim/Csound/FLOSS/audio
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
0dbfs = 1
nchnls = 7
vbaplsinit 2.01, 7, -40, 40, 70, 140, 180, -110, -70
vbaplsinit 2.02, 2, -40, 40
vbaplsinit 2.03, 3, -70, 180, 70
instr 1
aSnd, a0 soundin "ClassGuit.wav"
kAzim line 0, p3, -360
a1, a2, a3, a4, a5, a6, a7 vbap aSnd, kAzim, 0, 0, 1
outch 1, a1, 2, a2, 3, a3, 4, a4, 5, a5, 6, a6, 7, a7
endin
instr 2
aSnd, a0 soundin "ClassGuit.wav"
kAzim line 0, p3, -360
a1, a2 vbap aSnd, kAzim, 0, 0, 2
outch 1, a1, 2, a2
endin
instr 3
aSnd, a0 soundin "ClassGuit.wav"
kAzim line 0, p3, -360
a1, a2, a3 vbap aSnd, kAzim, 0, 0, 3
outch 7, a1, 3, a2, 5, a3
endin
</CsInstruments>
<CsScore>
i 1 0 6
i 2 6 6
i 3 12 6
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Instead of just one loudspeaker configuration, as in the previous examples, there are now three configurations:
vbaplsinit 2.01, 7, -40, 40, 70, 140, 180, -110, -70 vbaplsinit 2.02, 2, -40, 40 vbaplsinit 2.03, 3, -70, 180, 70
The first parameter (the number of dimensions) now has an additional fractional part, with a range from .01 to .99, specifying the number of the speaker layout. So 2.01 means: two dimensions, layout number one, 2.02 is layout number two, and 2.03 is layout number three. The new vbap opcode has now these parameters:
ar1[, ar2...] vbap asig, kazim [, kelev] [, kspread] [, ilayout]
The last parameter ilayout refers to the speaker layout number. In the example above, instrument 1 uses layout 1, instrument 2 uses layout 2, and instrument 3 uses layout 3. Even if you do not have more than two speakers you should see in Csound's output that instrument 1 goes to all seven speakers, instrument 2 only to the first two, and instrument 3 goes to speaker 3, 5, and 7.
In addition to the new vbap opcode, vbapg has been written. The idea is to have an opcode which returns the gains (amplitudes) of the speakers instead of the audio signal:
k1[, k2...] vbapg kazim [,kelev] [, kspread] [, ilayout]
Ambisonics
Ambisonics is another technique to distribute a virtual sound source in space.
There are excellent sources for the discussion of Ambisonics online3 and the following chapter will give a step by step introduction. We will focus just on the basic practicalities of using the Ambisonics opcodes of Csound, without going into too much detail of the concepts behind them.
Ambisonics works using two basic steps. In the first step you encode the sound and the spatial information (its localisation) of a virtual sound source in a so-called B-format. In the second step you decode the B-format to match your loudspeaker setup.
It is possible to save the B-format as its own audio file, to preserve the spatial information or you can immediately do the decoding after the encoding thereby dealing directly only with audio signals instead of Ambisonic files. The next example takes the latter approach by implementing a transformation of the VBAP circle example to Ambisonics.
EXAMPLE 05B08_Ambi_circle.csd
<CsoundSynthesizer> <CsOptions> -odac -d ;for the next line, change to your folder --env:SSDIR+=/home/jh/Joachim/Csound/FLOSS/Release01/Csound_Floss_Release01/audio </CsOptions> <CsInstruments> sr = 44100 ksmps = 32 0dbfs = 1 nchnls = 8 instr 1 Sfile = "ClassGuit.wav" iFilLen filelen Sfile p3 = iFilLen aSnd, a0 soundin Sfile kAzim line 0, p3, 360 ;counterclockwise (!) iSetup = 4 ;octogon aw, ax, ay, az bformenc1 aSnd, kAzim, 0 a1, a2, a3, a4, a5, a6, a7, a8 bformdec1 iSetup, aw, ax, ay, az outch 1, a1, 2, a2, 3, a3, 4, a4, 5, a5, 6, a6, 7, a7, 8, a8 endin </CsInstruments> <CsScore> i 1 0 1 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
The first thing to note is that for a counterclockwise circle, the azimuth now has the line 0 -> 360, instead of 0 -> -360 as was used in the VBAP example. This is because Ambisonics usually reads the angle in a mathematical way: a positive angle is counterclockwise. Next, the encoding process is carried out in the line:
aw, ax, ay, az bformenc1 aSnd, kAzim, 0
Input arguments are the monophonic sound source aSnd, the xy-angle kAzim, and the elevation angle which is set to zero. Output signals are the spatial information in x-, y- and z- direction (ax, ay, az), and also an omnidirectional signal called aw.
Decoding is performed by the line:
a1, a2, a3, a4, a5, a6, a7, a8 bformdec1 iSetup, aw, ax, ay, az
The inputs for the decoder are the same aw, ax, ay, az, which were the results of the encoding process, and an additional iSetup parameter. Currently the Csound decoder only works with some standard setups for the speaker: iSetup = 4 refers to an octogon.4 So the final eight audio signals a1, ..., a8 are being produced using this decoder, and are then sent to the speakers in the same way using the outch opcode.
Different Orders
What we have seen in this example is called 'first order' ambisonics. This means that the encoding process leads to the four basic dimensions w, x, y, z as described above.5 In "second order" ambisonics, there are additional "directions" called r, s, t, u, v. And in "third order" ambisonics again the additional k, l, m, n, o, p, q. The final example in this section shows the three orders, each of them in one instrument. If you have eight speakers in octophonic setup, you can compare the results.
EXAMPLE 05B09_Ambi_orders.csd
<CsoundSynthesizer> <CsOptions> -odac -d ;for the next line, change to your folder --env:SSDIR+=/home/jh/Joachim/Csound/FLOSS/Release01/Csound_Floss_Release01/audio </CsOptions> <CsInstruments> sr = 44100 ksmps = 32 0dbfs = 1 nchnls = 8 instr 1 ;first order aSnd, a0 soundin "ClassGuit.wav" kAzim line 0, p3, 360 iSetup = 4 ;octogon aw, ax, ay, az bformenc1 aSnd, kAzim, 0 a1, a2, a3, a4, a5, a6, a7, a8 bformdec1 iSetup, aw, ax, ay, az outch 1, a1, 2, a2, 3, a3, 4, a4, 5, a5, 6, a6, 7, a7, 8, a8 endin instr 2 ;second order aSnd, a0 soundin "ClassGuit.wav" kAzim line 0, p3, 360 iSetup = 4 ;octogon aw, ax, ay, az, ar, as, at, au, av bformenc1 aSnd, kAzim, 0 a1, a2, a3, a4, a5, a6, a7, a8 bformdec1 iSetup, aw, ax, ay, az, ar, as, at, au, av outch 1, a1, 2, a2, 3, a3, 4, a4, 5, a5, 6, a6, 7, a7, 8, a8 endin instr 3 ;third order aSnd, a0 soundin "ClassGuit.wav" kAzim line 0, p3, 360 iSetup = 4 ;octogon aw, ax, ay, az, ar, as, at, au, av, ak, al, am, an, ao, ap, aq bformenc1 aSnd, kAzim, 0 a1, a2, a3, a4, a5, a6, a7, a8 bformdec1 iSetup, aw, ax, ay, az, ar, as, at, au, av, ak, al, am, an, ao, ap, aq outch 1, a1, 2, a2, 3, a3, 4, a4, 5, a5, 6, a6, 7, a7, 8, a8 endin </CsInstruments> <CsScore> i 1 0 6 i 2 6 6 i 3 12 6 </CsScore> </CsoundSynthesizer> ;example by joachim heintz
In theory, first-order ambisonics need at least 4 speakers to be projected correctly. Second-order ambisonics needs at least 6 speakers (9, if 3 dimensions are employed). Third-order ambisonics need at least 8 speakers (or 16 for 3d). So, although higher order should in general lead to a better result in space, you cannot expect it to work unless you have a sufficient number of speakers. Of course practice over theory may prove to be a better judge in many cases.
Ambisonics UDOs
Usage of the ambisonics UDOs
This chapter gives an overview of the UDOs explained below.
The channels of the B-format are stored in a zak space. Call zakinit only once and put it outside of any instrument definition in the orchestra file after the header. zacl clears the za space and is called after decoding. The B format of order n can be decoded in any order <= n.
The text files "ambisonics_udos.txt", "ambisonics2D_udos.txt", "AEP_udos.txt" and "utilities.txt" must be located in the same folder as the csd files or included with full path.
These files can be downloaded together with the entire examples (some of them for CsoundQt) from here (as of September 2015).
zakinit isizea, isizek (isizea = (order + 1)^2 in ambisonics (3D); isizea = 2·order + 1 in ambi2D; isizek = 1) #include "ambisonics_udos.txt" (order <= 8) ambi_encode asnd, iorder, kazimuth, kelevation (azimuth, elevation in degrees) ambi_enc_dist asnd, iorder, kazimuth, kelevation, kdistance a1 [, a2] ... [, a8] ambi_decode iorder, ifn a1 [, a2] ... [, a8] ambi_dec_inph iorder, ifn f ifn 0 n -2 p1 az1 el1 az2 el2 ... (n is a power of 2 greater than 3·number_of_spekers + 1) (p1 is not used) ambi_write_B "name", iorder, ifile_format (ifile_format see fout in the csound help) ambi_read_B "name", iorder (only <= 5) kaz, kel, kdist xyz_to_aed kx, ky, kz ;#include "ambisonics2D_udos.txt" ambi2D_encode asnd, iorder, kazimuth (any order) (azimuth in degrees) ambi2D_enc_dist asnd, iorder, kazimuth, kdistance a1 [, a2] ... [, a8] ambi2D_decode iorder, iaz1 [, iaz2] ... [, iaz8] a1 [, a2] ... [, a8] ambi2D_dec_inph iorder, iaz1 [, iaz2] ... [, iaz8] (order <= 12) ambi2D_write_B "name", iorder, ifile_format ambi2D_read_B "name", iorder (order <= 19) kaz, kdist xy_to_ad kx, ky #include "AEP_udos.txt" (any order integer or fractional) a1 [, a2] ... [, a16] AEP_xyz asnd, korder, ifn, kx, ky, kz, kdistance f ifn 0 64 -2 max_speaker_distance x1 y1 z1 x2 y2 z2 ... a1 [, a2] ... [, a8] AEP asnd, korder, ifn, kazimuth, kelevation, kdistance (azimuth, elevation in degrees) f ifn 0 64 -2 max_speaker_distance az1 el1 dist1 az2 el2 dist2 ... (azimuth, elevation in degrees) ;#include "ambi_utilities.txt" kdist dist kx, ky kdist dist kx, ky, kz ares Doppler asnd, kdistance ares absorb asnd, kdistance kx, ky, kz aed_to_xyz kazimuth, kelevation, kdistance ix, iy, iz aed_to_xyz iazimuth, ielevation, idistance a1 [, a2] ... [, a16] dist_corr a1 [, a2] ... [, a16], ifn f ifn 0 32 -2 max_speaker_distance dist1, dist2, ... (distances in m) irad radiani idegree krad radian kdegree arad radian adegree idegree degreei irad kdegree degree krad adegree degree arad
Introduction
In the following introduction we will explain the principles of ambisonics step by step and write an opcode for every step. The opcodes above combine all of the functionality described. Since the two-dimensional analogy to Ambisonics is easier to understand and to implement with a simple equipment, we shall fully explain it first.
Ambisonics is a technique of three-dimensional sound projection. The information about the recorded or synthesized sound field is encoded and stored in several channels, taking no account of the arrangement of the loudspeakers for reproduction. The encoding of a signal's spatial information can be more or less precise, depending on the so-called order of the algorithm used. Order zero corresponds to the monophonic signal and requires only one channel for storage and reproduction. In first-order Ambisonics, three further channels are used to encode the portions of the sound field in the three orthogonal directions x, y and z. These four channels constitute the so-called first-order B-format. When Ambisonics is used for artificial spatialisation of recorded or synthesized sound, the encoding can be of an arbitrarily high order. The higher orders cannot be interpreted as easily as orders zero and one.
In a two-dimensional analogy to Ambisonics (called Ambisonics2D in what follows), only sound waves in the horizontal plane are encoded.
The loudspeaker feeds are obtained by decoding the B-format signal. The resulting panning is amplitude panning, and only the direction to the sound source is taken into account.
The illustration below shows the principle of Ambisonics. First a sound is generated and its position determined. The amplitude and spectrum are adjusted to simulate distance, the latter using a low-pass filter. Then the Ambisonic encoding is computed using the sound's coordinates. Encoding mth order B-format requires n = (m+1)^2 channels (n = 2m + 1 channels in Ambisonics2D). By decoding the B-format, one can obtain the signals for any number (>= n) of loudspeakers in any arrangement. Best results are achieved with symmetrical speaker arrangements.
If the B-format does not need to be recorded the speaker signals can be calculated at low cost and arbitrary order using so-called ambisonics equivalent panning (AEP).
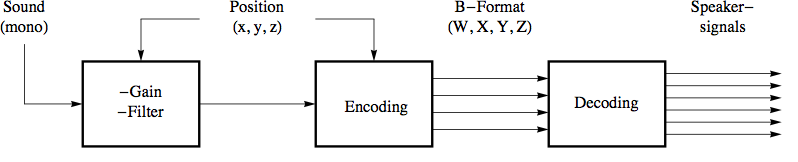
Ambisonics2D
Introduction
We will first explain the encoding process in Ambisonics2D. The position of a sound source in the horizontal plane is given by two coordinates. In Cartesian coordinates (x, y) the listener is at the origin of the coordinate system (0, 0), and the x-coordinate points to the front, the y-coordinate to the left. The position of the sound source can also be given in polar coordinates by the angle ψ between the line of vision of the listener (front) and the direction to the sound source, and by their distance r. Cartesian coordinates can be converted to polar coordinates by the formulae:
r = and ψ = arctan(x, y),
polar to Cartesian coordinates by
x = r·cos(ψ) and y = r·sin(ψ).
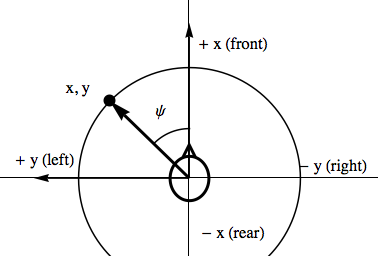
The 0th order B-Format of a signal S of a sound source on the unit circle is just the mono signal: W0 = W = S. The first order B-Format contains two additional channels: W1,1 = X = S·cos(ψ) = S·x and W1,2 = Y = S·sin(ψ) = S·y, i.e. the product of the Signal S with the sine and the cosine of the direction ψ of the sound source. The B-Format higher order contains two additional channels per order m: Wm, 1 = S·cos(mψ) and Wm, 2 = S·sin(mψ).
W0 = S
W1,1 = X = S·cos(ψ) = S·x W1,2 = Y = S·sin(ψ) = S·y
W2,1 = S·cos(2ψ) W2,2 = S·sin(2ψ)
...
Wm,1 = S·cos(mψ) Wm,2 = S·sin(mψ)
From the n = 2m + 1 B-Format channels the loudspeaker signals pi of n loudspeakers which are set up symmetrically on a circle (with angle ϕi) are:
pi = 1/n(W0 + 2W1,1cos(ϕi) + 2W1,2sin(ϕi) + 2W2,1cos(2ϕi) + 2W2,2sin(2ϕi) + ...)
= 2/n(1/2 W0 + W1,1cos(ϕi) + W1,2sin(ϕi) + W2,1cos(2ϕi) + W2,2sin(2ϕi) + ...)
(If more than n speakers are used, we can use the same formula)
In the Csound example udo_ambisonics2D_1.csd the opcode ambi2D_encode_1a produces the 3 channels W, X and Y (a0, a11, a12) from an input sound and the angle ψ (azmuth kaz), the opcode ambi2D_decode_1_8 decodes them to 8 speaker signals a1, a2, ..., a8. The inputs of the decoder are the 3 channels a0, a11, a12 and the 8 angles of the speakers.
EXAMPLE 05B10_udo_ambisonics2D_1.csd
<CsoundSynthesizer>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 8
0dbfs = 1
; ambisonics2D first order without distance encoding
; decoding for 8 speakers symmetrically positioned on a circle
; produces the 3 channels 1st order; input: asound, kazimuth
opcode ambi2D_encode_1a, aaa, ak
asnd,kaz xin
kaz = $M_PI*kaz/180
a0 = asnd
a11 = cos(kaz)*asnd
a12 = sin(kaz)*asnd
xout a0,a11,a12
endop
; decodes 1st order to a setup of 8 speakers at angles i1, i2, ...
opcode ambi2D_decode_1_8, aaaaaaaa, aaaiiiiiiii
a0,a11,a12,i1,i2,i3,i4,i5,i6,i7,i8 xin
i1 = $M_PI*i1/180
i2 = $M_PI*i2/180
i3 = $M_PI*i3/180
i4 = $M_PI*i4/180
i5 = $M_PI*i5/180
i6 = $M_PI*i6/180
i7 = $M_PI*i7/180
i8 = $M_PI*i8/180
a1 = (.5*a0 + cos(i1)*a11 + sin(i1)*a12)*2/3
a2 = (.5*a0 + cos(i2)*a11 + sin(i2)*a12)*2/3
a3 = (.5*a0 + cos(i3)*a11 + sin(i3)*a12)*2/3
a4 = (.5*a0 + cos(i4)*a11 + sin(i4)*a12)*2/3
a5 = (.5*a0 + cos(i5)*a11 + sin(i5)*a12)*2/3
a6 = (.5*a0 + cos(i6)*a11 + sin(i6)*a12)*2/3
a7 = (.5*a0 + cos(i7)*a11 + sin(i7)*a12)*2/3
a8 = (.5*a0 + cos(i8)*a11 + sin(i8)*a12)*2/3
xout a1,a2,a3,a4,a5,a6,a7,a8
endop
instr 1
asnd rand .05
kaz line 0,p3,3*360 ;turns around 3 times in p3 seconds
a0,a11,a12 ambi2D_encode_1a asnd,kaz
a1,a2,a3,a4,a5,a6,a7,a8 \
ambi2D_decode_1_8 a0,a11,a12,
0,45,90,135,180,225,270,315
outc a1,a2,a3,a4,a5,a6,a7,a8
endin
</CsInstruments>
<CsScore>
i1 0 40
</CsScore>
</CsoundSynthesizer>
;example by martin neukom
The B-format of all events of all instruments can be summed before decoding. Thus in the example udo_ambisonics2D_2.csd we create a zak space with 21 channels (zakinit 21, 1) for the 2D B-format up to 10th order where the encoded signals are accumulated. The opcode ambi2D_encode_3 shows how to produce the 7 B-format channels a0, a11, a12, ..., a32 for third order. The opcode ambi2D_encode_n produces the 2(n+1) channels a0, a11, a12, ..., a32 for any order n (needs zakinit 2(n+1), 1). The opcode ambi2D_decode_basic is an overloaded function i.e. it decodes to n speaker signals depending on the number of in- and outputs given (in this example only for 1 or 2 speakers). Any number of instruments can play arbitrary often. Instrument 10 decodes for the first 4 speakers of an 18 speaker setup.
EXAMPLE 05B11_udo_ambisonics2D_2.csd
<CsoundSynthesizer> <CsInstruments> sr = 44100 ksmps = 32 nchnls = 4 0dbfs = 1 ; ambisonics2D encoding fifth order ; decoding for 8 speakers symmetrically positioned on a circle ; all instruments write the B-format into a buffer (zak space) ; instr 10 decodes ; zak space with the 21 channels of the B-format up to 10th order zakinit 21, 1 ;explicit encoding third order opcode ambi2D_encode_3, 0, ak asnd,kaz xin kaz = $M_PI*kaz/180 zawm asnd,0 zawm cos(kaz)*asnd,1 ;a11 zawm sin(kaz)*asnd,2 ;a12 zawm cos(2*kaz)*asnd,3 ;a21 zawm sin(2*kaz)*asnd,4 ;a22 zawm cos(3*kaz)*asnd,5 ;a31 zawm sin(3*kaz)*asnd,6 ;a32 endop ; encoding arbitrary order n(zakinit 2*n+1, 1) opcode ambi2D_encode_n, 0, aik asnd,iorder,kaz xin kaz = $M_PI*kaz/180 kk = iorder c1: zawm cos(kk*kaz)*asnd,2*kk-1 zawm sin(kk*kaz)*asnd,2*kk kk = kk-1 if kk > 0 goto c1 zawm asnd,0 endop ; basic decoding for arbitrary order n for 1 speaker opcode ambi2D_decode_basic, a, ii iorder,iaz xin iaz = $M_PI*iaz/180 igain = 2/(2*iorder+1) kk = iorder a1 = .5*zar(0) c1: a1 += cos(kk*iaz)*zar(2*kk-1) a1 += sin(kk*iaz)*zar(2*kk) kk = kk-1 if kk > 0 goto c1 xout igain*a1 endop ; decoding for 2 speakers opcode ambi2D_decode_basic, aa, iii iorder,iaz1,iaz2 xin iaz1 = $M_PI*iaz1/180 iaz2 = $M_PI*iaz2/180 igain = 2/(2*iorder+1) kk = iorder a1 = .5*zar(0) c1: a1 += cos(kk*iaz1)*zar(2*kk-1) a1 += sin(kk*iaz1)*zar(2*kk) kk = kk-1 if kk > 0 goto c1 kk = iorder a2 = .5*zar(0) c2: a2 += cos(kk*iaz2)*zar(2*kk-1) a2 += sin(kk*iaz2)*zar(2*kk) kk = kk-1 if kk > 0 goto c2 xout igain*a1,igain*a2 endop instr 1 asnd rand p4 ares reson asnd,p5,p6,1 kaz line 0,p3,p7*360 ;turns around p7 times in p3 seconds ambi2D_encode_n asnd,10,kaz endin instr 2 asnd oscil p4,p5,1 kaz line 0,p3,p7*360 ;turns around p7 times in p3 seconds ambi2D_encode_n asnd,10,kaz endin instr 10 ;decode all insruments (the first 4 speakers of a 18 speaker setup) a1,a2 ambi2D_decode_basic 10,0,20 a3,a4 ambi2D_decode_basic 10,40,60 outc a1,a2,a3,a4 zacl 0,20 ; clear the za variables endin </CsInstruments> <CsScore> f1 0 32768 10 1 ; amp cf bw turns i1 0 3 .7 1500 12 1 i1 2 18 .1 2234 34 -8 ; amp fr 0 turns i2 0 3 .1 440 0 2 i10 0 3 </CsScore> </CsoundSynthesizer> ;example by martin neukom
In-phase Decoding
The left figure below shows a symmetrical arrangement of 7 loudspeakers. If the virtual sound source is precisely in the direction of a loudspeaker, only this loudspeaker gets a signal (center figure). If the virtual sound source is between two loudspeakers, these loudspeakers receive the strongest signals; all other loudspeakers have weaker signals, some with negative amplitude, that is, reversed phase (right figure).
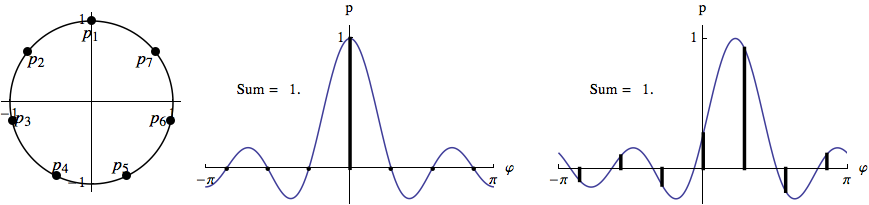
To avoid having loudspeaker sounds that are far away from the virtual sound source and to ensure that negative amplitudes (inverted phase) do not arise, the B-format channels can be weighted before being decoded. The weighting factors depend on the highest order used (M) and the order of the particular channel being decoded (m).
gm = (M!)^2/((M + m)!·(M - m)!)
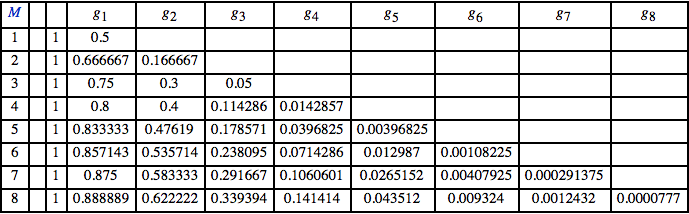
The decoded signal can be normalised with the factor gnorm(M) = (2M + 1) !/(4^M (M!)^2)

The illustration below shows a third-order B-format signal decoded to 13 loudspeakers first uncorrected (so-called basic decoding, left), then corrected by weighting (so-called in-phase decoding, right).
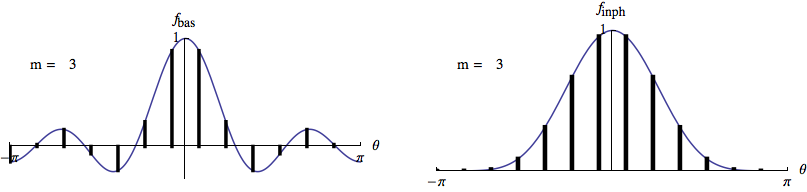
Example udo_ambisonics2D_3.csd shows in-phase decoding. The weights and norms up to 12th order are saved in the arrays iWeight2D[][] and iNorm2D[] respectively. Instrument 11 decodes third order for 4 speakers in a square.
EXAMPLE 05B12_udo_ambisonics2D_3.csd
<CsoundSynthesizer> <CsInstruments> sr = 44100 ksmps = 32 nchnls = 4 0dbfs = 1 opcode ambi2D_encode_n, 0, aik asnd,iorder,kaz xin kaz = $M_PI*kaz/180 kk = iorder c1: zawm cos(kk*kaz)*asnd,2*kk-1 zawm sin(kk*kaz)*asnd,2*kk kk = kk-1 if kk > 0 goto c1 zawm asnd,0 endop ;in-phase-decoding opcode ambi2D_dec_inph, a, ii ; weights and norms up to 12th order iNorm2D[] array 1,0.75,0.625,0.546875,0.492188,0.451172,0.418945, 0.392761,0.370941,0.352394,0.336376,0.322360 iWeight2D[][] init 12,12 iWeight2D array 0.5,0,0,0,0,0,0,0,0,0,0,0, 0.666667,0.166667,0,0,0,0,0,0,0,0,0,0, 0.75,0.3,0.05,0,0,0,0,0,0,0,0,0, 0.8,0.4,0.114286,0.0142857,0,0,0,0,0,0,0,0, 0.833333,0.47619,0.178571,0.0396825,0.00396825,0,0,0,0,0,0,0, 0.857143,0.535714,0.238095,0.0714286,0.012987,0.00108225,0,0,0,0,0,0, 0.875,0.583333,0.291667,0.1060601,0.0265152,0.00407925,0.000291375,0,0,0,0,0, 0.888889,0.622222,0.339394,0.141414,0.043512,0.009324,0.0012432, 0.0000777,0,0,0,0, 0.9,0.654545,0.381818,0.176224,0.0629371,0.0167832,0.00314685, 0.000370218,0.0000205677,0,0,0, 0.909091,0.681818,0.41958,0.20979,0.0839161,0.0262238,0.0061703, 0.00102838,0.000108251,0.00000541254,0,0, 0.916667,0.705128,0.453297,0.241758,0.105769,0.0373303,0.0103695, 0.00218306,0.000327459,0.0000311866,0.00000141757,0, 0.923077,0.725275,0.483516,0.271978,0.12799,0.0497738,0.015718, 0.00392951,0.000748478,0.000102065,0.00000887523,0.000000369801 iorder,iaz1 xin iaz1 = $M_PI*iaz1/180 kk = iorder a1 = .5*zar(0) c1: a1 += cos(kk*iaz1)*iWeight2D[iorder-1][kk-1]*zar(2*kk-1) a1 += sin(kk*iaz1)*iWeight2D[iorder-1][kk-1]*zar(2*kk) kk = kk-1 if kk > 0 goto c1 xout iNorm2D[iorder-1]*a1 endop zakinit 7, 1 instr 1 asnd rand p4 ares reson asnd,p5,p6,1 kaz line 0,p3,p7*360 ;turns around p7 times in p3 seconds ambi2D_encode_n asnd,3,kaz endin instr 11 a1 ambi2D_dec_inph 3,0 a2 ambi2D_dec_inph 3,90 a3 ambi2D_dec_inph 3,180 a4 ambi2D_dec_inph 3,270 outc a1,a2,a3,a4 zacl 0,6 ; clear the za variables endin </CsInstruments> <CsScore> ; amp cf bw turns i1 0 3 .1 1500 12 1 i11 0 3 </CsScore> </CsoundSynthesizer> ;example by martin neukom
Distance
In order to simulate distances and movements of sound sources, the signals have to be treated before being encoded. The main perceptual cues for the distance of a sound source are reduction of the amplitude, filtering due to the absorbtion of the air and the relation between direct and indirect sound. We will implement the first two of these cues. The amplitude arriving at a listener is inversely proportional to the distance of the sound source. If the distance is larger than the unit circle (not necessarily the radius of the speaker setup, which does not need to be known when encoding sounds) we can simply divide the sound by the distance. With this calculation inside the unit circle the amplitude is amplified and becomes infinite when the distance becomes zero. Another problem arises when a virtual sound source passes the origin. The amplitude of the speaker signal in the direction of the movement suddenly becomes maximal and the signal of the opposite speaker suddenly becomes zero. A simple solution for these problems is to limit the gain of the channel W inside the unit circle to 1 (f1 in the figure below) and to fade out all other channels (f2). By fading out all channels except channel W the information about the direction of the sound source is lost and all speaker signals are the same and the sum of the speaker signals reaches its maximum when the distance is 0.

Now, we are looking for gain functions that are smoother at d = 1. The functions should be differentiable and the slope of f1 at distance d = 0 should be 0. For distances greater than 1 the functions should be approximately 1/d. In addition the function f1 should continuously grow with decreasing distance and reach its maximum at d = 0. The maximal gain must be 1. The function atan(d·π/2)/(d·π/2) fulfills these constraints. We create a function f2 for the fading out of the other channels by multiplying f1 by the factor (1 – E^(-d)).
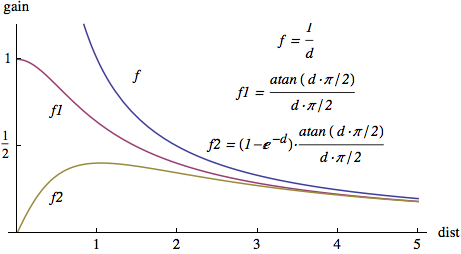
In example udo_ambisonics2D_4 the UDO ambi2D_enc_dist_n encodes a sound at any order with distance correction. The inputs of the UDO are asnd, iorder, kazimuth and kdistance. If the distance becomes negative the azimuth angle is turned to its opposite (kaz += π) and the distance taken positive.
EXAMPLE 05B13_udo_ambisonics2D_4.csd
<CsoundSynthesizer>
<CsOptions>
--env:SSDIR+=../SourceMaterials -odac -m0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 8
0dbfs = 1
#include "../SourceMaterials/ambisonics2D_udos.txt"
; distance encoding
; with any distance (includes zero and negative distance)
opcode ambi2D_enc_dist_n, 0, aikk
asnd,iorder,kaz,kdist xin
kaz = $M_PI*kaz/180
kaz = (kdist < 0 ? kaz + $M_PI : kaz)
kdist = abs(kdist)+0.0001
kgainW = taninv(kdist*1.5707963) / (kdist*1.5708) ;pi/2
kgainHO = (1 - exp(-kdist))*kgainW
kk = iorder
asndW = kgainW*asnd
asndHO = kgainHO*asndW
c1:
zawm cos(kk*kaz)*asndHO,2*kk-1
zawm sin(kk*kaz)*asndHO,2*kk
kk = kk-1
if kk > 0 goto c1
zawm asndW,0
endop
zakinit 17, 1
instr 1
asnd rand p4
;asnd soundin "/Users/user/csound/ambisonic/violine.aiff"
kaz line 0,p3,p5*360 ;turns around p5 times in p3 seconds
kdist line p6,p3,p7
ambi2D_enc_dist_n asnd,8,kaz,kdist
endin
instr 10
a1,a2,a3,a4,
a5,a6,a7,a8 ambi2D_decode 8,0,45,90,135,180,225,270,315
outc a1,a2,a3,a4,a5,a6,a7,a8
zacl 0,16
endin
</CsInstruments>
<CsScore>
f1 0 32768 10 1
; amp turns dist1 dist2
i1 0 4 1 0 2 -2
;i1 0 4 1 1 1 1
i10 0 4
</CsScore>
</CsoundSynthesizer>
;example by martin neukom
In order to simulate the absorption of the air we introduce a very simple lowpass filter with a distance depending cutoff frequency. We produce a Doppler-shift with a distance dependent delay of the sound. Now, we have to determine our unit since the delay of the sound wave is calculated as distance divided by sound velocity. In our example udo_ambisonics2D_5.csd we set the unit to 1 metre. These procedures are performed before the encoding. In instrument 1 the movement of the sound source is defined in Cartesian coordinates. The UDO xy_to_ad transforms them into polar coordinates. The B-format channels can be written to a sound file with the opcode fout. The UDO write_ambi2D_2 writes the channels up to second order into a sound file.
EXAMPLE 05B14_udo_ambisonics2D_5.csd
<CsoundSynthesizer>
<CsOptions>
--env:SSDIR+=../SourceMaterials -odac -m0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 8
0dbfs = 1
#include "../SourceMaterials/ambisonics2D_udos.txt"
#include "../SourceMaterials/ambisonics_utilities.txt" ;opcodes Absorb and Doppler
/* these opcodes are included in "ambisonics2D_udos.txt"
opcode xy_to_ad, kk, kk
kx,ky xin
kdist = sqrt(kx*kx+ky*ky)
kaz taninv2 ky,kx
xout 180*kaz/$M_PI, kdist
endop
opcode Absorb, a, ak
asnd,kdist xin
aabs tone 5*asnd,20000*exp(-.1*kdist)
xout aabs
endop
opcode Doppler, a, ak
asnd,kdist xin
abuf delayr .5
adop deltapi interp(kdist)*0.0029137529 + .01 ; 1/343.2
delayw asnd
xout adop
endop
*/
opcode write_ambi2D_2, 0, S
Sname xin
fout Sname,12,zar(0),zar(1),zar(2),zar(3),zar(4)
endop
zakinit 17, 1 ; zak space with the 17 channels of the B-format
instr 1
asnd buzz p4,p5,50,1
;asnd soundin "/Users/user/csound/ambisonic/violine.aiff"
kx line p7,p3,p8
ky line p9,p3,p10
kaz,kdist xy_to_ad kx,ky
aabs absorb asnd,kdist
adop Doppler .2*aabs,kdist
ambi2D_enc_dist adop,5,kaz,kdist
endin
instr 10 ;decode all insruments
a1,a2,a3,a4,
a5,a6,a7,a8 ambi2D_dec_inph 5,0,45,90,135,180,225,270,315
outc a1,a2,a3,a4,a5,a6,a7,a8
; fout "B_format2D.wav",12,zar(0),zar(1),zar(2),zar(3),zar(4),
; zar(5),zar(6),zar(7),zar(8),zar(9),zar(10)
write_ambi2D_2 "ambi_ex5.wav"
zacl 0,16 ; clear the za variables
endin
</CsInstruments>
<CsScore>
f1 0 32768 10 1
; amp f 0 x1 x2 y1 y2
i1 0 5 .8 200 0 40 -20 1 .1
i10 0 5
</CsScore>
</CsoundSynthesizer>
;example by martin neukom
The position of a point in space can be given by its Cartesian coordinates x, y and z or by its spherical coordinates the radial distance r from the origin of the coordinate system, the elevation δ (which lies between –π and π) and the azimuth angle θ.
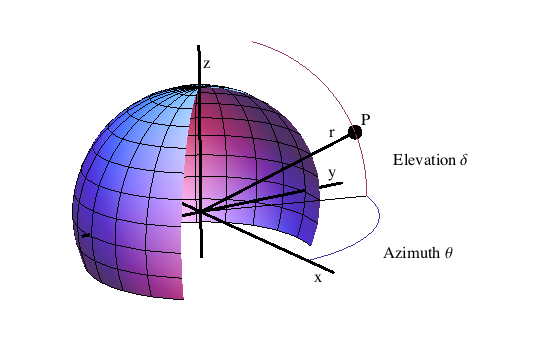
The formulae for transforming coordinates are as follows:
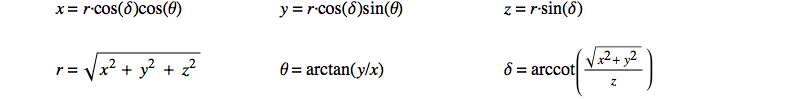
The channels of the Ambisonic B-format are computed as the product of the sounds themselves and the so-called spherical harmonics representing the direction to the virtual sound sources. The spherical harmonics can be normalised in various ways. We shall use the so-called semi-normalised spherical harmonics. The following table shows the encoding functions up to the third order as function of azimuth and elevation Ymn(θ,δ) and as function of x, y and z Ymn(x,y,z) for sound sources on the unit sphere. The decoding formulae for symmetrical speaker setups are the same.
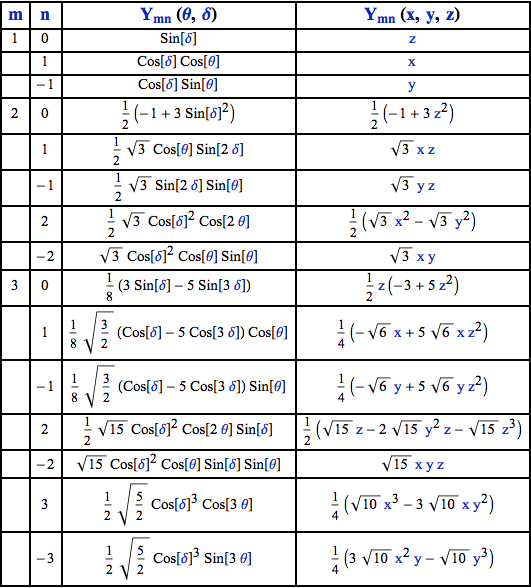
In the first 3 of the following examples we will not produce sound but display in number boxes (for example using CsoundQt widgets) the amplitude of 3 speakers at positions (1, 0, 0), (0, 1, 0) and (0, 0, 1) in Cartesian coordinates. The position of the sound source can be changed with the two scroll numbers. The example udo_ambisonics_1.csd shows encoding up to second order. The decoding is done in two steps. First we decode the B-format for one speaker. In the second step, we create a overloaded opcode for n speakers. The number of output signals determines which version of the opcode is used. The opcodes ambi_encode and ambi_decode up to 8th order are saved in the text file "ambisonics_udos.txt".
EXAMPLE 05B15_udo_ambisonics_1.csd
<CsoundSynthesizer> <CsInstruments> sr = 44100 ksmps = 32 nchnls = 1 0dbfs = 1 zakinit 9, 1 ; zak space with the 9 channel B-format second order opcode ambi_encode, 0, aikk asnd,iorder,kaz,kel xin kaz = $M_PI*kaz/180 kel = $M_PI*kel/180 kcos_el = cos(kel) ksin_el = sin(kel) kcos_az = cos(kaz) ksin_az = sin(kaz) zawm asnd,0 ; W zawm kcos_el*ksin_az*asnd,1 ; Y = Y(1,-1) zawm ksin_el*asnd,2 ; Z = Y(1,0) zawm kcos_el*kcos_az*asnd,3 ; X = Y(1,1) if iorder < 2 goto end i2 = sqrt(3)/2 kcos_el_p2 = kcos_el*kcos_el ksin_el_p2 = ksin_el*ksin_el kcos_2az = cos(2*kaz) ksin_2az = sin(2*kaz) kcos_2el = cos(2*kel) ksin_2el = sin(2*kel) zawm i2*kcos_el_p2*ksin_2az*asnd,4 ; V = Y(2,-2) zawm i2*ksin_2el*ksin_az*asnd,5 ; S = Y(2,-1) zawm .5*(3*ksin_el_p2 - 1)*asnd,6 ; R = Y(2,0) zawm i2*ksin_2el*kcos_az*asnd,7 ; S = Y(2,1) zawm i2*kcos_el_p2*kcos_2az*asnd,8 ; U = Y(2,2) end: endop ; decoding of order iorder for 1 speaker at position iaz,iel,idist opcode ambi_decode1, a, iii iorder,iaz,iel xin iaz = $M_PI*iaz/180 iel = $M_PI*iel/180 a0=zar(0) if iorder > 0 goto c0 aout = a0 goto end c0: a1=zar(1) a2=zar(2) a3=zar(3) icos_el = cos(iel) isin_el = sin(iel) icos_az = cos(iaz) isin_az = sin(iaz) i1 = icos_el*isin_az ; Y = Y(1,-1) i2 = isin_el ; Z = Y(1,0) i3 = icos_el*icos_az ; X = Y(1,1) if iorder > 1 goto c1 aout = (1/2)*(a0 + i1*a1 + i2*a2 + i3*a3) goto end c1: a4=zar(4) a5=zar(5) a6=zar(6) a7=zar(7) a8=zar(8) ic2 = sqrt(3)/2 icos_el_p2 = icos_el*icos_el isin_el_p2 = isin_el*isin_el icos_2az = cos(2*iaz) isin_2az = sin(2*iaz) icos_2el = cos(2*iel) isin_2el = sin(2*iel) i4 = ic2*icos_el_p2*isin_2az ; V = Y(2,-2) i5 = ic2*isin_2el*isin_az ; S = Y(2,-1) i6 = .5*(3*isin_el_p2 - 1) ; R = Y(2,0) i7 = ic2*isin_2el*icos_az ; S = Y(2,1) i8 = ic2*icos_el_p2*icos_2az ; U = Y(2,2) aout = (1/9)*(a0 + 3*i1*a1 + 3*i2*a2 + 3*i3*a3 + 5*i4*a4 + 5*i5*a5 + 5*i6*a6 + 5*i7*a7 + 5*i8*a8) end: xout aout endop ; overloaded opcode for decoding of order iorder ; speaker positions in function table ifn opcode ambi_decode, a,ii iorder,ifn xin xout ambi_decode1(iorder,table(1,ifn),table(2,ifn)) endop opcode ambi_decode, aa,ii iorder,ifn xin xout ambi_decode1(iorder,table(1,ifn),table(2,ifn)), ambi_decode1(iorder,table(3,ifn),table(4,ifn)) endop opcode ambi_decode, aaa,ii iorder,ifn xin xout ambi_decode1(iorder,table(1,ifn),table(2,ifn)), ambi_decode1(iorder,table(3,ifn),table(4,ifn)), ambi_decode1(iorder,table(5,ifn),table(6,ifn)) endop instr 1 asnd init 1 ;kdist init 1 kaz invalue "az" kel invalue "el" ambi_encode asnd,2,kaz,kel ao1,ao2,ao3 ambi_decode 2,17 outvalue "sp1", downsamp(ao1) outvalue "sp2", downsamp(ao2) outvalue "sp3", downsamp(ao3) zacl 0,8 endin </CsInstruments> <CsScore> ;f1 0 1024 10 1 f17 0 64 -2 0 0 0 90 0 0 90 0 0 0 0 0 0 i1 0 100 </CsScore> </CsoundSynthesizer> ;example by martin neukom
Example udo_ambisonics_2.csd shows in-phase decoding. The weights up to 8th order are stored in the arrays iWeight3D[][].
EXAMPLE 05B16_udo_ambisonics_2.csd
<CsoundSynthesizer>
<CsOptions>
--env:SSDIR+=../SourceMaterials -odac -m0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
zakinit 81, 1 ; zak space for up to 81 channels of the 8th order B-format
; the opcodes used below are safed in "ambisonics_udos.txt"
#include "../SourceMaterials/ambisonics_udos.txt"
; in-phase decoding up to third order for one speaker
opcode ambi_dec1_inph3, a, iii
; weights up to 8th order
iWeight3D[][] init 8,8
iWeight3D array 0.333333,0,0,0,0,0,0,0,
0.5,0.1,0,0,0,0,0,0,
0.6,0.2,0.0285714,0,0,0,0,0,
0.666667,0.285714,0.0714286,0.0079365,0,0,0,0,
0.714286,0.357143,0.119048,0.0238095,0.0021645,0,0,0,
0.75,0.416667,0.166667,0.0454545,0.00757576,0.00058275,0,0,
0.777778,0.466667,0.212121,0.0707071,0.016317,0.002331,0.0001554,0,
0.8,0.509091,0.254545,0.0979021,0.027972,0.0055944,0.0006993,0.00004114
iorder,iaz,iel xin
iaz = $M_PI*iaz/180
iel = $M_PI*iel/180
a0=zar(0)
if iorder > 0 goto c0
aout = a0
goto end
c0:
a1=iWeight3D[iorder-1][0]*zar(1)
a2=iWeight3D[iorder-1][0]*zar(2)
a3=iWeight3D[iorder-1][0]*zar(3)
icos_el = cos(iel)
isin_el = sin(iel)
icos_az = cos(iaz)
isin_az = sin(iaz)
i1 = icos_el*isin_az ; Y = Y(1,-1)
i2 = isin_el ; Z = Y(1,0)
i3 = icos_el*icos_az ; X = Y(1,1)
if iorder > 1 goto c1
aout = (3/4)*(a0 + i1*a1 + i2*a2 + i3*a3)
goto end
c1:
a4=iWeight3D[iorder-1][1]*zar(4)
a5=iWeight3D[iorder-1][1]*zar(5)
a6=iWeight3D[iorder-1][1]*zar(6)
a7=iWeight3D[iorder-1][1]*zar(7)
a8=iWeight3D[iorder-1][1]*zar(8)
ic2 = sqrt(3)/2
icos_el_p2 = icos_el*icos_el
isin_el_p2 = isin_el*isin_el
icos_2az = cos(2*iaz)
isin_2az = sin(2*iaz)
icos_2el = cos(2*iel)
isin_2el = sin(2*iel)
i4 = ic2*icos_el_p2*isin_2az ; V = Y(2,-2)
i5 = ic2*isin_2el*isin_az ; S = Y(2,-1)
i6 = .5*(3*isin_el_p2 - 1) ; R = Y(2,0)
i7 = ic2*isin_2el*icos_az ; S = Y(2,1)
i8 = ic2*icos_el_p2*icos_2az ; U = Y(2,2)
aout = (1/3)*(a0 + 3*i1*a1 + 3*i2*a2 + 3*i3*a3 + 5*i4*a4 + 5*i5*a5 + 5*i6*a6 + 5*i7*a7 + 5*i8*a8)
end:
xout aout
endop
; overloaded opcode for decoding for 1 or 2 speakers
; speaker positions in function table ifn
opcode ambi_dec2_inph, a,ii
iorder,ifn xin
xout ambi_dec1_inph(iorder,table(1,ifn),table(2,ifn))
endop
opcode ambi_dec2_inph, aa,ii
iorder,ifn xin
xout ambi_dec1_inph(iorder,table(1,ifn),table(2,ifn)),
ambi_dec1_inph(iorder,table(3,ifn),table(4,ifn))
endop
opcode ambi_dec2_inph, aaa,ii
iorder,ifn xin
xout ambi_dec1_inph(iorder,table(1,ifn),table(2,ifn)),
ambi_dec1_inph(iorder,table(3,ifn),table(4,ifn)),
ambi_dec1_inph(iorder,table(5,ifn),table(6,ifn))
endop
instr 1
asnd init 1
kdist init 1
kaz invalue "az"
kel invalue "el"
ambi_encode asnd,8,kaz,kel
ao1,ao2,ao3 ambi_dec_inph 8,17
outvalue "sp1", downsamp(ao1)
outvalue "sp2", downsamp(ao2)
outvalue "sp3", downsamp(ao3)
zacl 0,80
endin
</CsInstruments>
<CsScore>
f1 0 1024 10 1
f17 0 64 -2 0 0 0 90 0 0 90 0 0 0 0 0 0 0 0 0 0
i1 0 100
</CsScore>
</CsoundSynthesizer>
;example by martin neukom
The weighting factors for in-phase decoding of Ambisonics (3D) are:
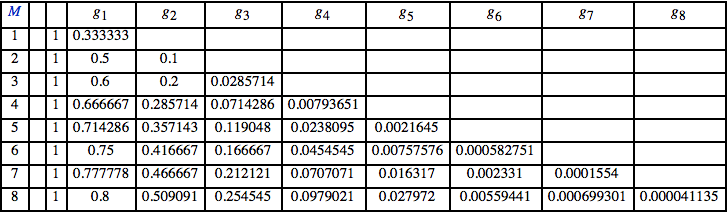
Example udo_ambisonics_3.csd shows distance encoding.
EXAMPLE 05B17_udo_ambisonics_3.csd
<CsoundSynthesizer>
<CsOptions>
--env:SSDIR+=../SourceMaterials -odac -m0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
zakinit 81, 1 ; zak space with the 11 channels of the B-format
#include "../SourceMaterials/ambisonics_udos.txt"
opcode ambi3D_enc_dist1, 0, aikkk
asnd,iorder,kaz,kel,kdist xin
kaz = $M_PI*kaz/180
kel = $M_PI*kel/180
kaz = (kdist < 0 ? kaz + $M_PI : kaz)
kel = (kdist < 0 ? -kel : kel)
kdist = abs(kdist)+0.00001
kgainW = taninv(kdist*1.5708) / (kdist*1.5708)
kgainHO = (1 - exp(-kdist)) ;*kgainW
outvalue "kgainHO", kgainHO
outvalue "kgainW", kgainW
kcos_el = cos(kel)
ksin_el = sin(kel)
kcos_az = cos(kaz)
ksin_az = sin(kaz)
asnd = kgainW*asnd
zawm asnd,0 ; W
asnd = kgainHO*asnd
zawm kcos_el*ksin_az*asnd,1 ; Y = Y(1,-1)
zawm ksin_el*asnd,2 ; Z = Y(1,0)
zawm kcos_el*kcos_az*asnd,3 ; X = Y(1,1)
if iorder < 2 goto end
/*
...
*/
end:
endop
instr 1
asnd init 1
kaz invalue "az"
kel invalue "el"
kdist invalue "dist"
ambi_enc_dist asnd,5,kaz,kel,kdist
ao1,ao2,ao3,ao4 ambi_decode 5,17
outvalue "sp1", downsamp(ao1)
outvalue "sp2", downsamp(ao2)
outvalue "sp3", downsamp(ao3)
outvalue "sp4", downsamp(ao4)
outc 0*ao1,0*ao2;,2*ao3,2*ao4
zacl 0,80
endin
</CsInstruments>
<CsScore>
f17 0 64 -2 0 0 0 90 0 180 0 0 90 0 0 0 0
i1 0 100
</CsScore>
</CsoundSynthesizer>
;example by martin neukom
In example udo_ambisonics_4.csd a buzzer with the three-dimensional trajectory shown below is encoded in third order and decoded for a speaker setup in a cube (f17).
EXAMPLE 05B18_udo_ambisonics_4.csd
<CsoundSynthesizer>
<CsOptions>
--env:SSDIR+=../SourceMaterials -odac -m0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 8
0dbfs = 1
zakinit 16, 1
#include "../SourceMaterials/ambisonics_udos.txt"
#include "../SourceMaterials/ambisonics_utilities.txt"
instr 1
asnd buzz p4,p5,p6,1
kt line 0,p3,p3
kaz,kel,kdist xyz_to_aed 10*sin(kt),10*sin(.78*kt),10*sin(.43*kt)
adop Doppler asnd,kdist
ambi_enc_dist adop,3,kaz,kel,kdist
a1,a2,a3,a4,a5,a6,a7,a8 ambi_decode 3,17
;k0 ambi_write_B "B_form.wav",8,14
outc a1,a2,a3,a4,a5,a6,a7,a8
zacl 0,15
endin
</CsInstruments>
<CsScore>
f1 0 32768 10 1
f17 0 64 -2 0 -45 35.2644 45 35.2644 135 35.2644 225 35.2644 -45 -35.2644 .7854 -35.2644 135 -35.2644 225 -35.2644
i1 0 40 .5 300 40
</CsScore>
</CsoundSynthesizer>
;example by martin neukom
Ambisonics Equivalent Panning (AEP)
If we combine encoding and in-phase decoding, we obtain the following panning function (a gain function for a speaker depending on its distance to a virtual sound source):
P(γ, m) = (1/2+ 1/2 cos γ)^m
where γ denotes the angle between a sound source and a speaker and m denotes the order. If the speakers are positioned on a unit sphere the cosine of the angle γ is calculated as the scalar product of the vector to the sound source (x, y, z) and the vector to the speaker (xs, ys, zs).
In contrast to Ambisonics the order indicated in the function does not have to be an integer. This means that the order can be continuously varied during decoding. The function can be used in both Ambisonics and Ambisonics2D.
This system of panning is called Ambisonics Equivalent Panning. It has the disadvantage of not producing a B-format representation, but its implementation is straightforward and the computation time is short and independent of the Ambisonics order simulated. Hence it is particularly useful for real-time applications, for panning in connection with sequencer programs and for experimentation with high and non-integral Ambisonic orders.
The opcode AEP1 in the example udo_AEP.csd shows the calculation of ambisonics equivalent panning for one speaker. The opcode AEP then uses AEP1 to produce the signals for several speakers. In the text file "AEP_udos.txt" AEP ist implemented for up to 16 speakers. The position of the speakers must be written in a function table. As the first parameter in the function table the maximal speaker distance must be given.
EXAMPLE 05B19_udo_AEP.csd
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 4
0dbfs = 1
;#include "ambisonics_udos.txt"
; opcode AEP1 is the same as in udo_AEP_xyz.csd
opcode AEP1, a, akiiiikkkkkk ; soundin, order, ixs, iys, izs, idsmax, kx, ky, kz
ain,korder,ixs,iys,izs,idsmax,kx,ky,kz,kdist,kfade,kgain xin
idists = sqrt(ixs*ixs+iys*iys+izs*izs)
kpan = kgain*((1-kfade+kfade*(kx*ixs+ky*iys+kz*izs)/(kdist*idists))^korder)
xout ain*kpan*idists/idsmax
endop
; opcode AEP calculates ambisonics equivalent panning for n speaker
; the number n of output channels defines the number of speakers (overloaded function)
; inputs: sound ain, order korder (any real number >= 1)
; ifn = number of the function containing the speaker positions
; position and distance of the sound source kaz,kel,kdist in degrees
opcode AEP, aaaa, akikkk
ain,korder,ifn,kaz,kel,kdist xin
kaz = $M_PI*kaz/180
kel = $M_PI*kel/180
kx = kdist*cos(kel)*cos(kaz)
ky = kdist*cos(kel)*sin(kaz)
kz = kdist*sin(kel)
ispeaker[] array 0,
table(3,ifn)*cos(($M_PI/180)*table(2,ifn))*cos(($M_PI/180)*table(1,ifn)),
table(3,ifn)*cos(($M_PI/180)*table(2,ifn))*sin(($M_PI/180)*table(1,ifn)),
table(3,ifn)*sin(($M_PI/180)*table(2,ifn)),
table(6,ifn)*cos(($M_PI/180)*table(5,ifn))*cos(($M_PI/180)*table(4,ifn)),
table(6,ifn)*cos(($M_PI/180)*table(5,ifn))*sin(($M_PI/180)*table(4,ifn)),
table(6,ifn)*sin(($M_PI/180)*table(5,ifn)),
table(9,ifn)*cos(($M_PI/180)*table(8,ifn))*cos(($M_PI/180)*table(7,ifn)),
table(9,ifn)*cos(($M_PI/180)*table(8,ifn))*sin(($M_PI/180)*table(7,ifn)),
table(9,ifn)*sin(($M_PI/180)*table(8,ifn)),
table(12,ifn)*cos(($M_PI/180)*table(11,ifn))*cos(($M_PI/180)*table(10,ifn)),
table(12,ifn)*cos(($M_PI/180)*table(11,ifn))*sin(($M_PI/180)*table(10,ifn)),
table(12,ifn)*sin(($M_PI/180)*table(11,ifn))
idsmax table 0,ifn
kdist = kdist+0.000001
kfade = .5*(1 - exp(-abs(kdist)))
kgain = taninv(kdist*1.5708)/(kdist*1.5708)
a1 AEP1 ain,korder,ispeaker[1],ispeaker[2],ispeaker[3],
idsmax,kx,ky,kz,kdist,kfade,kgain
a2 AEP1 ain,korder,ispeaker[4],ispeaker[5],ispeaker[6],
idsmax,kx,ky,kz,kdist,kfade,kgain
a3 AEP1 ain,korder,ispeaker[7],ispeaker[8],ispeaker[9],
idsmax,kx,ky,kz,kdist,kfade,kgain
a4 AEP1 ain,korder,ispeaker[10],ispeaker[11],ispeaker[12],
idsmax,kx,ky,kz,kdist,kfade,kgain
xout a1,a2,a3,a4
endop
instr 1
ain rand 1
;ain soundin "/Users/user/csound/ambisonic/violine.aiff"
kt line 0,p3,360
korder init 24
;kdist Dist kx, ky, kz
a1,a2,a3,a4 AEP ain,korder,17,kt,0,1
outc a1,a2,a3,a4
endin
</CsInstruments>
<CsScore>
;fuction for speaker positions
; GEN -2, parameters: max_speaker_distance, xs1,ys1,zs1,xs2,ys2,zs2,...
;octahedron
;f17 0 32 -2 1 1 0 0 -1 0 0 0 1 0 0 -1 0 0 0 1 0 0 -1
;cube
;f17 0 32 -2 1,732 1 1 1 1 1 -1 1 -1 1 -1 1 1
;octagon
;f17 0 32 -2 1 0.924 -0.383 0 0.924 0.383 0 0.383 0.924 0 -0.383 0.924 0 -0.924 0.383 0 -0.924 -0.383 0 -0.383 -0.924 0 0.383 -0.924 0
;f17 0 32 -2 1 0 0 1 45 0 1 90 0 1 135 0 1 180 0 1 225 0 1 270 0 1 315 0 1
;f17 0 32 -2 1 0 -90 1 0 -70 1 0 -50 1 0 -30 1 0 -10 1 0 10 1 0 30 1 0 50 1
f17 0 32 -2 1 -45 0 1 45 0 1 135 0 1 225 0 1
i1 0 2
</CsScore>
</CsoundSynthesizer>
;example by martin neukom
Utilities
The file utilities.txt contains the following opcodes:
dist computes the distance from the origin (0, 0) or (0, 0, 0) to a point (x, y) or (x, y, z)
kdist dist kx, ky
kdist dist kx, ky, kz
Doppler simulates the Doppler-shift
ares Doppler asnd, kdistance
absorb is a very simple simulation of the frequency dependent absorption
ares absorb asnd, kdistance
aed_to_xyz converts polar coordinates to Cartesian coordinates
kx, ky, kz aed_to_xyz kazimuth, kelevation, kdistance
ix, iy, iz aed_to_xyz iazimuth, ielevation, idistance
dist_corr induces a delay and reduction of the speaker signals relative to the most distant speaker.
a1 [, a2] ... [, a16] dist_corr a1 [, a2] ... [, a16], ifn
f ifn 0 32 -2 max_speaker_distance dist1, dist2, ... ;distances in m
radian (radiani) converts degrees to radians.
irad radiani idegree
krad radian kdegree
arad radian adegree
degree (degreei) converts radian to degrees
idegree degreei irad
kdegree degree krad
adegree degree arad
VBAP or Ambisonics?
Csound offers a simple and reliable way to access two standard methods for multi-channel spatialisation. Both have different qualities and follow different aesthetics. VBAP can perhaps be described as clear, rational and direct. It combines simplicity with flexibility. It gives a reliable sound projection even for rather asymmetric speaker setups. Ambisonics on the other hand offers a very soft sound image, in which the single speaker becomes part of a coherent sound field. The B-format offers the possibility to store the spatial information independently from any particular speaker configuration.
The composer, or spatial interpreter, can choose one or the other technique depending on the music and the context. Or (s)he can design a personal approach to spatialisation by combining the different techniques described in this chapter.
- First described by Ville Pulkki in 1997: Ville Pulkki, Virtual source positioning using vector base amplitude panning, in: Journal of the Audio Engeneering Society, 45(6), 456-466^
- Ville Pulkki, Uniform spreading of amplitude panned virtual sources, in: Proceedings of the 1999 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, Mohonk Montain House, New Paltz^
- For instance www.ambisonic.net or www.icst.net/research/projects/ambisonics-theory^
- See www.csounds.com/manual/html/bformdec1.html for more details.^
- Which in turn then are taken by the decoder as input.^
FILTERS
Audio filters can range from devices that subtly shape the tonal characteristics of a sound to ones that dramatically remove whole portions of a sound spectrum to create new sounds. Csound includes several versions of each of the commonest types of filters and some more esoteric ones also. The full list of Csound's standard filters can be found here. A list of the more specialised filters can be found here.
Lowpass Filters
The first type of filter encountered is normally the lowpass filter. As its name suggests it allows lower frequencies to pass through unimpeded and therefore filters higher frequencies. The crossover frequency is normally referred to as the 'cutoff' frequency. Filters of this type do not really cut frequencies off at the cutoff point like a brick wall but instead attenuate increasingly according to a cutoff slope. Different filters offer cutoff slopes of different of steepness. Another aspect of a lowpass filter that we may be concerned with is a ripple that might emerge at the cutoff point. If this is exaggerated intentionally it is referred to as resonance or 'Q'.
In the following example, three lowpass filters filters are demonstrated: tone, butlp and moogladder. tone offers a quite gentle cutoff slope and therefore is better suited to subtle spectral enhancement tasks. butlp is based on the Butterworth filter design and produces a much sharper cutoff slope at the expense of a slightly greater CPU overhead. moogladder is an interpretation of an analogue filter found in a moog synthesizer – it includes a resonance control.
In the example a sawtooth waveform is played in turn through each filter. Each time the cutoff frequency is modulated using an envelope, starting high and descending low so that more and more of the spectral content of the sound is removed as the note progresses. A sawtooth waveform has been chosen as it contains strong higher frequencies and therefore demonstrates the filters characteristics well; a sine wave would be a poor choice of source sound on account of its lack of spectral richness.
EXAMPLE 05C01_tone_butlp_moogladder.csd
<CsoundSynthesizer>
<CsOptions>
-odac ; activates real time sound output
</CsOptions>
<CsInstruments>
; Example by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
instr 1
prints "tone%n" ; indicate filter type in console
aSig vco2 0.5, 150 ; input signal is a sawtooth waveform
kcf expon 10000,p3,20 ; descending cutoff frequency
aSig tone aSig, kcf ; filter audio signal
out aSig ; filtered audio sent to output
endin
instr 2
prints "butlp%n" ; indicate filter type in console
aSig vco2 0.5, 150 ; input signal is a sawtooth waveform
kcf expon 10000,p3,20 ; descending cutoff frequency
aSig butlp aSig, kcf ; filter audio signal
out aSig ; filtered audio sent to output
endin
instr 3
prints "moogladder%n" ; indicate filter type in console
aSig vco2 0.5, 150 ; input signal is a sawtooth waveform
kcf expon 10000,p3,20 ; descending cutoff frequency
aSig moogladder aSig, kcf, 0.9 ; filter audio signal
out aSig ; filtered audio sent to output
endin
</CsInstruments>
<CsScore>
; 3 notes to demonstrate each filter in turn
i 1 0 3; tone
i 2 4 3; butlp
i 3 8 3; moogladder
e
</CsScore>
</CsoundSynthesizer>
Highpass Filters
A highpass filter is the converse of a lowpass filter; frequencies higher than the cutoff point are allowed to pass whilst those lower are attenuated. atone and buthp are the analogues of tone and butlp. Resonant highpass filters are harder to find but Csound has one in bqrez. bqrez is actually a multi-mode filter and could also be used as a resonant lowpass filter amongst other things. We can choose which mode we want by setting one of its input arguments appropriately. Resonant highpass is mode 1. In this example a sawtooth waveform is again played through each of the filters in turn but this time the cutoff frequency moves from low to high. Spectral content is increasingly removed but from the opposite spectral direction.
EXAMPLE 05C02_atone_buthp_bqrez.csd
<CsoundSynthesizer>
<CsOptions>
-odac ; activates real time sound output
</CsOptions>
<CsInstruments>
; Example by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
instr 1
prints "atone%n" ; indicate filter type in console
aSig vco2 0.2, 150 ; input signal is a sawtooth waveform
kcf expon 20, p3, 20000 ; define envelope for cutoff frequency
aSig atone aSig, kcf ; filter audio signal
out aSig ; filtered audio sent to output
endin
instr 2
prints "buthp%n" ; indicate filter type in console
aSig vco2 0.2, 150 ; input signal is a sawtooth waveform
kcf expon 20, p3, 20000 ; define envelope for cutoff frequency
aSig buthp aSig, kcf ; filter audio signal
out aSig ; filtered audio sent to output
endin
instr 3
prints "bqrez(mode:1)%n" ; indicate filter type in console
aSig vco2 0.03, 150 ; input signal is a sawtooth waveform
kcf expon 20, p3, 20000 ; define envelope for cutoff frequency
aSig bqrez aSig, kcf, 30, 1 ; filter audio signal
out aSig ; filtered audio sent to output
endin
</CsInstruments>
<CsScore>
; 3 notes to demonstrate each filter in turn
i 1 0 3 ; atone
i 2 5 3 ; buthp
i 3 10 3 ; bqrez(mode 1)
e
</CsScore>
</CsoundSynthesizer>
Bandpass Filters
A bandpass filter allows just a narrow band of sound to pass through unimpeded and as such is a little bit like a combination of a lowpass and highpass filter connected in series. We normally expect at least one additional parameter of control: control over the width of the band of frequencies allowed to pass through, or 'bandwidth'.
In the next example cutoff frequency and bandwidth are demonstrated independently for two different bandpass filters offered by Csound. First of all a sawtooth waveform is passed through a reson filter and a butbp filter in turn while the cutoff frequency rises (bandwidth remains static). Then pink noise is passed through reson and butbp in turn again but this time the cutoff frequency remains static at 5000Hz while the bandwidth expands from 8 to 5000Hz. In the latter two notes it will be heard how the resultant sound moves from almost a pure sine tone to unpitched noise. butbp is obviously the Butterworth based bandpass filter. reson can produce dramatic variations in amplitude depending on the bandwidth value and therefore some balancing of amplitude in the output signal may be necessary if out of range samples and distortion are to be avoided. Fortunately the opcode itself includes two modes of amplitude balancing built in but by default neither of these methods are active and in this case the use of the balance opcode may be required. Mode 1 seems to work well with spectrally sparse sounds like harmonic tones while mode 2 works well with spectrally dense sounds such as white or pink noise.
EXAMPLE 05C03_reson_butbp.csd
<CsoundSynthesizer> <CsOptions> -odac ; activates real time sound output </CsOptions> <CsInstruments> ; Example by Iain McCurdy sr = 44100 ksmps = 32 nchnls = 1 0dbfs = 1 instr 1 prints "reson%n" ; indicate filter type in console aSig vco2 0.5, 150 ; input signal: sawtooth waveform kcf expon 20,p3,10000 ; rising cutoff frequency aSig reson aSig,kcf,kcf*0.1,1 ; filter audio signal out aSig ; send filtered audio to output endin instr 2 prints "butbp%n" ; indicate filter type in console aSig vco2 0.5, 150 ; input signal: sawtooth waveform kcf expon 20,p3,10000 ; rising cutoff frequency aSig butbp aSig, kcf, kcf*0.1 ; filter audio signal out aSig ; send filtered audio to output endin instr 3 prints "reson%n" ; indicate filter type in console aSig pinkish 0.5 ; input signal: pink noise kbw expon 10000,p3,8 ; contracting bandwidth aSig reson aSig, 5000, kbw, 2 ; filter audio signal out aSig ; send filtered audio to output endin instr 4 prints "butbp%n" ; indicate filter type in console aSig pinkish 0.5 ; input signal: pink noise kbw expon 10000,p3,8 ; contracting bandwidth aSig butbp aSig, 5000, kbw ; filter audio signal out aSig ; send filtered audio to output endin </CsInstruments> <CsScore> i 1 0 3 ; reson - cutoff frequency rising i 2 4 3 ; butbp - cutoff frequency rising i 3 8 6 ; reson - bandwidth increasing i 4 15 6 ; butbp - bandwidth increasing e </CsScore> </CsoundSynthesizer>
Comb Filtering
A comb filter is a special type of filter that creates a harmonically related stack of resonance peaks on an input sound file. A comb filter is really just a very short delay effect with feedback. Typically the delay times involved would be less than 0.05 seconds. Many of the comb filters documented in the Csound Manual term this delay time, 'loop time'. The fundamental of the harmonic stack of resonances produced will be 1/loop time. Loop time and the frequencies of the resonance peaks will be inversely proportional – as loop time gets smaller, the frequencies rise. For a loop time of 0.02 seconds, the fundamental resonance peak will be 50Hz, the next peak 100Hz, the next 150Hz and so on. Feedback is normally implemented as reverb time – the time taken for amplitude to drop to 1/1000 of its original level or by 60dB. This use of reverb time as opposed to feedback alludes to the use of comb filters in the design of reverb algorithms. Negative reverb times will result in only the odd numbered partials of the harmonic stack being present.
The following example demonstrates a comb filter using the vcomb opcode. This opcode allows for performance time modulation of the loop time parameter. For the first 5 seconds of the demonstration the reverb time increases from 0.1 seconds to 2 while the loop time remains constant at 0.005 seconds. Then the loop time decreases to 0.0005 seconds over 6 seconds (the resonant peaks rise in frequency), finally over the course of 10 seconds the loop time rises to 0.1 seconds (the resonant peaks fall in frequency). A repeating noise impulse is used as a source sound to best demonstrate the qualities of a comb filter.
EXAMPLE 05C04_comb.csd
<CsoundSynthesizer>
<CsOptions>
-odac ;activates real time sound output
</CsOptions>
<CsInstruments>
;Example by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
instr 1
; -- generate an input audio signal (noise impulses) --
; repeating amplitude envelope:
kEnv loopseg 1,0, 0,1,0.005,1,0.0001,0,0.9949,0
aSig pinkish kEnv*0.6 ; pink noise pulses
; apply comb filter to input signal
krvt linseg 0.1, 5, 2 ; reverb time
alpt expseg 0.005,5,0.005,6,0.0005,10,0.1,1,0.1 ; loop time
aRes vcomb aSig, krvt, alpt, 0.1 ; comb filter
out aRes ; audio to output
endin
</CsInstruments>
<CsScore>
i 1 0 25
e
</CsScore>
</CsoundSynthesizer>
Other Filters Worth Investigating
In addition to a wealth of low and highpass filters, Csound offers several more unique filters. Multimode such as bqrez provide several different filter types within a single opcode. Filter type is normally chosen using an i-rate input argument that functions like a switch. Another multimode filter, clfilt, offers additional filter controls such as 'filter design' and 'number of poles' to create unusual sound filters. unfortunately some parts of this opcode are not implemented yet.
eqfil is essentially a parametric equaliser but multiple iterations could be used as modules in a graphic equaliser bank. In addition to the capabilities of eqfil, pareq adds the possibility of creating low and high shelving filtering which might prove useful in mastering or in spectral adjustment of more developed sounds.
rbjeq offers a quite comprehensive multimode filter including highpass, lowpass, bandpass, bandreject, peaking, low-shelving and high-shelving, all in a single opcode
statevar offers the outputs from four filter types - highpass, lowpass, bandpass and bandreject - simultaneously so that the user can morph between them smoothly. svfilter does a similar thing but with just highpass, lowpass and bandpass filter types.
phaser1 and phaser2 offer algorithms containing chains of first order and second order allpass filters respectively. These algorithms could conceivably be built from individual allpass filters, but these ready-made versions provide convenience and added efficiency.
hilbert is a specialist IIR filter that implements the Hilbert transformer.
For those wishing to devise their own filter using coefficients Csound offers filter2 and zfilter2.
Filter Comparision
The following example shows a nice comparision between a number of common used filters.
EXAMPLE 05C05_filter_compar.csd
<CsoundSynthesizer>
<CsOptions>
-odac -m128
</CsOptions>
<CsInstruments>
; comparison of filters with PAD timbre
; written by Anton Kholomiov, 2016
; based on the Jacob Joaquin wobble bass sound
sr = 44100
ksmps = 64
nchnls = 2
0dbfs = 1
gaOut init 0
giSpb init 0.45
; Filter types
#define MOOG_LADDER #1#
#define MOOG_VCF #2#
#define LPF18 #3#
#define BQREZ #4#
#define CLFILT #5#
#define BUTTERLP #6#
#define LOWRES #7#
#define REZZY #8#
#define SVFILTER #9#
#define VLOWRES #10#
#define STATEVAR #11#
#define MVCLPF1 #12#
#define MVCLPF2 #13#
#define MVCLPF3 #14#
opcode Echo, 0, S
Smsg xin
printf_i "\n%s\n\n", 1, Smsg
endop
opcode EchoFilterName, 0, i
iType xin
if iType == $MOOG_LADDER then
Echo "moogladder"
elseif iType == $MOOG_VCF then
Echo "moogvcf"
elseif iType == $LPF18 then
Echo "lpf18"
elseif iType == $BQREZ then
Echo "bqrez"
elseif iType == $CLFILT then
Echo "clfilt"
elseif iType == $BUTTERLP then
Echo "butterlp"
elseif iType == $LOWRES then
Echo "lowres"
elseif iType == $REZZY then
Echo "rezzy"
elseif iType == $SVFILTER then
Echo "svfilter"
elseif iType == $VLOWRES then
Echo "vlowres"
elseif iType == $STATEVAR then
Echo "statevar"
elseif iType == $MVCLPF1 then
Echo "mvclpf1"
elseif iType == $MVCLPF2 then
Echo "mvclpf2"
elseif iType == $MVCLPF3 then
Echo "mvclpf3"
else
endif
endop
opcode MultiFilter, a, akki
ain, kcfq, kres, iType xin
kType init iType
if kType == $MOOG_LADDER then
aout moogladder ain, kcfq, kres
elseif kType == $MOOG_VCF then
aout moogvcf ain, kcfq, kres
elseif kType == $LPF18 then
aout lpf18 ain, kcfq, kres, 0.5
elseif kType == $BQREZ then
aout bqrez ain, kcfq, 99 * kres + 1
elseif kType == $CLFILT then
aout clfilt ain, kcfq, 0, 2
elseif kType == $BUTTERLP then
aout butterlp ain, kcfq
elseif kType == $LOWRES then
aout lowres ain, kcfq, kres
elseif kType == $REZZY then
aout rezzy ain, kcfq, kres
elseif kType == $SVFILTER then
aout, ahigh, aband svfilter ain, kcfq, (499 / 10) * kres + 1 ; rescales to make it musical
elseif kType == $VLOWRES then
aout vlowres ain, kcfq, kres, 2, 0
elseif kType == $STATEVAR then
ahp, aout, abp, abr statevar ain, kcfq, kres
elseif kType == $MVCLPF1 then
aout mvclpf1 ain, kcfq, kres
elseif kType == $MVCLPF2 then
aout mvclpf2 ain, kcfq, kres
elseif kType == $MVCLPF3 then
aout mvclpf3 ain, kcfq, kres
else
aout = 0
endif
xout aout
endop
opcode Wave, a, k
kcps xin
asqr vco2 1, kcps * 0.495, 10 ; square
asaw vco2 1, kcps * 1.005, 0 ; wave
xout 0.5 * (asqr + asaw)
endop
opcode Filter, a, aiii
ain, iFilterType, iCoeff, iCps xin
iDivision = 1 / (iCoeff * giSpb)
kLfo loopseg iDivision, 0, 0, 0, 0.5, 1, 0.5, 0
iBase = iCps
iMod = iBase * 9
kcfq = iBase + iMod * kLfo
kres init 0.6
aout MultiFilter ain, kcfq, kres, iFilterType
aout balance aout, ain
xout aout
endop
opcode Reverb, aa, aaii
adryL, adryR, ifeedback, imix xin
awetL, awetR reverbsc adryL, adryR, ifeedback, 10000
aoutL = (1 - imix) * adryL + imix * awetL
aoutR = (1 - imix) * adryR + imix * awetR
xout aoutL, aoutR
endop
instr Bass
iCoeff = p4
iCps = p5
iFilterType = p6
aWave Wave iCps
aOut Filter aWave, iFilterType, iCoeff, iCps
aOut linen aOut, .01, p3, .1
gaOut = gaOut + aOut
endin
opcode Note, 0, iiii
idt = 2 * giSpb
iNum, iCoeff, iPch, iFilterType xin
event_i "i", "Bass", idt * iNum, idt, iCoeff, cpspch(iPch), iFilterType
endop
instr Notes
iFilterType = p4
EchoFilterName iFilterType
Note 0, 2, 6.04, iFilterType
Note 1, 1/3, 7.04, iFilterType
Note 2, 2, 6.04, iFilterType
Note 3, 1/1.5, 7.07, iFilterType
Note 4, 2, 5.09, iFilterType
Note 5, 1, 6.09, iFilterType
Note 6, 1/1.5, 5.09, iFilterType
Note 7, 1/3, 6.11, iFilterType
Note 8, 1, 6.04, iFilterType
Note 9, 1/3, 7.04, iFilterType
Note 10, 2, 6.04, iFilterType
Note 11, 1/1.5, 7.07, iFilterType
Note 12, 2, 6.09, iFilterType
Note 13, 1, 7.09, iFilterType
Note 14, 1/1.5, 6.11, iFilterType
Note 15, 1/3, 6.07, iFilterType
Note 16, 2, 6.04, iFilterType
Note 17, 1/3, 7.04, iFilterType
Note 18, 2, 6.04, iFilterType
Note 19, 1/1.5, 7.07, iFilterType
turnoff
endin
opcode TrigNotes, 0, ii
iNum, iFilterType xin
idt = 20
event_i "i", "Notes", idt * iNum, 0, iFilterType
endop
instr PlayAll
iMixLevel = p4
event_i "i", "Main", 0, (14 * 20), iMixLevel
TrigNotes 0, $MOOG_LADDER
TrigNotes 1, $MOOG_VCF
TrigNotes 2, $LPF18
TrigNotes 3, $BQREZ
TrigNotes 4, $CLFILT
TrigNotes 5, $BUTTERLP
TrigNotes 6, $LOWRES
TrigNotes 7, $REZZY
TrigNotes 8, $SVFILTER
TrigNotes 9, $VLOWRES
TrigNotes 10, $STATEVAR
TrigNotes 11, $MVCLPF1
TrigNotes 12, $MVCLPF2
TrigNotes 13, $MVCLPF3
turnoff
endin
opcode DumpNotes, 0, iiSi
iNum, iFilterType, SFile, iMixLevel xin
idt = 30
Sstr sprintf {{i "%s" %f %f "%s" %f}}, "Dump", idt * iNum, idt, SFile, iMixLevel
scoreline_i Sstr
event_i "i", "Notes", idt * iNum, 0, iFilterType
endop
instr DumpAll
iMixLevel = p4
DumpNotes 0, $MOOG_LADDER, "moogladder-dubstep.wav", iMixLevel
DumpNotes 1, $MOOG_VCF, "moogvcf-dubstep.wav", iMixLevel
DumpNotes 2, $LPF18 , "lpf18-dubstep.wav", iMixLevel
DumpNotes 3, $BQREZ, "bqrez-dubstep.wav", iMixLevel
DumpNotes 4, $CLFILT, "clfilt-dubstep.wav", iMixLevel
DumpNotes 5, $BUTTERLP, "butterlp-dubstep.wav", iMixLevel
DumpNotes 6, $LOWRES, "lowres-dubstep.wav", iMixLevel
DumpNotes 7, $REZZY, "rezzy-dubstep.wav", iMixLevel
DumpNotes 8, $SVFILTER, "svfilter-dubstep.wav", iMixLevel
DumpNotes 9, $VLOWRES , "vlowres-dubstep.wav", iMixLevel
DumpNotes 10, $STATEVAR, "statevar-dubstep.wav", iMixLevel
DumpNotes 11, $MVCLPF1 , "mvclpf1-dubstep.wav", iMixLevel
DumpNotes 12, $MVCLPF2 , "mvclpf2-dubstep.wav", iMixLevel
DumpNotes 13, $MVCLPF3 , "mvclpf3-dubstep.wav", iMixLevel
turnoff
endin
instr Main
iVolume = 0.2
iReverbFeedback = 0.3
iMixLevel = p4
aoutL, aoutR Reverb gaOut, gaOut, iReverbFeedback, iMixLevel
outs (iVolume * aoutL), (iVolume * aoutR)
gaOut = 0
endin
instr Dump
SFile = p4
iMixLevel = p5
iVolume = 0.2
iReverbFeedback = 0.85
aoutL, aoutR Reverb gaOut, gaOut, iReverbFeedback, iMixLevel
fout SFile, 14, (iVolume * aoutL), (iVolume * aoutR)
gaOut = 0
endin
</CsInstruments>
<CsScore>
; the fourth parameter is a reverb mix level
i "PlayAll" 0 1 0.35
; uncomment to save output to wav files
;i "DumpAll" 0 1 0.35
</CsScore>
</CsoundSynthesizer>
DELAY AND FEEDBACK
A delay in DSP is a special kind of buffer, sometimes called a circular buffer. The length of this buffer is finite and must be declared upon initialization as it is stored in RAM. One way to think of the circular buffer is that as new items are added at the beginning of the buffer the oldest items at the end of the buffer are being 'shoved' out.
Besides their typical application for creating echo effects, delays can also be used to implement chorus, flanging, pitch shifting and filtering effects.
Csound offers many opcodes for implementing delays. Some of these offer varying degrees of quality - often balanced against varying degrees of efficiency whilst some are for quite specialized purposes.
To begin with, this section is going to focus upon a pair of opcodes, delayr and delayw. Whilst not the most efficient to use in terms of the number of lines of code required, the use of delayr and delayw helps to clearly illustrate how a delay buffer works. Besides this, delayr and delayw actually offer a lot more flexibility and versatility than many of the other delay opcodes.
When using delayr and delayw the establishement of a delay buffer is broken down into two steps: reading from the end of the buffer using delayr (and by doing this defining the length or duration of the buffer) and then writing into the beginning of the buffer using delayw.
The code employed might look like this:
aSigOut delayr 1
delayw aSigIn
where 'aSigIn' is the input signal written into the beginning of the buffer and 'aSigOut' is the output signal read from the end of the buffer. The fact that we declare reading from the buffer before writing to it is sometimes initially confusing but, as alluded to before, one reason this is done is to declare the length of the buffer. The buffer length in this case is 1 second and this will be the apparent time delay between the input audio signal and audio read from the end of the buffer.
The following example implements the delay described above in a .csd file. An input sound of sparse sine tone pulses is created. This is written into the delay buffer from which a new audio signal is created by read from the end of this buffer. The input signal (sometimes referred to as the dry signal) and the delay output signal (sometimes referred to as the wet signal) are mixed and set to the output. The delayed signal is attenuated with respect to the input signal.
EXAMPLE 05D01_delay.csd
<CsoundSynthesizer>
<CsOptions>
-odac ; activates real time sound output
</CsOptions>
<CsInstruments>
; Example by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giSine ftgen 0, 0, 2^12, 10, 1 ; a sine wave
instr 1
; -- create an input signal: short 'blip' sounds --
kEnv loopseg 0.5, 0, 0, 0,0.0005, 1 , 0.1, 0, 1.9, 0, 0
kCps randomh 400, 600, 0.5
aEnv interp kEnv
aSig poscil aEnv, kCps, giSine
; -- create a delay buffer --
aBufOut delayr 0.3
delayw aSig
; -- send audio to output (input and output to the buffer are mixed)
out aSig + (aBufOut*0.4)
endin
</CsInstruments>
<CsScore>
i 1 0 25
e
</CsScore>
</CsoundSynthesizer>
If we mix some of the delayed signal into the input signal that is written into the buffer then we will delay some of the delayed signal thus creating more than a single echo from each input sound. Typically the sound that is fed back into the delay input is attenuated, so that sound cycles through the buffer indefinitely but instead will eventually die away. We can attenuate the feedback signal by multiplying it by a value in the range zero to 1. The rapidity with which echoes will die away is defined by how close to zero this value is. The following example implements a simple delay with feedback.
EXAMPLE 05D02_delay_feedback.csd
<CsoundSynthesizer>
<CsOptions>
-odac ;activates real time sound output
</CsOptions>
<CsInstruments>
;Example by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giSine ftgen 0, 0, 2^12, 10, 1 ; a sine wave
instr 1
; -- create an input signal: short 'blip' sounds --
kEnv loopseg 0.5,0,0,0,0.0005,1,0.1,0,1.9,0,0 ; repeating envelope
kCps randomh 400, 600, 0.5 ; 'held' random values
aEnv interp kEnv ; a-rate envelope
aSig poscil aEnv, kCps, giSine ; generate audio
; -- create a delay buffer --
iFdback = 0.7 ; feedback ratio
aBufOut delayr 0.3 ; read audio from end of buffer
; write audio into buffer (mix in feedback signal)
delayw aSig+(aBufOut*iFdback)
; send audio to output (mix the input signal with the delayed signal)
out aSig + (aBufOut*0.4)
endin
</CsInstruments>
<CsScore>
i 1 0 25
e
</CsScore>
</CsoundSynthesizer>
Constructing a delay effect in this way is rather limited as the delay time is static. If we want to change the delay time we need to reinitialise the code that implements the delay buffer. A more flexible approach is to read audio from within the buffer using one of Csounds opcodes for 'tapping' a delay buffer, deltap, deltapi, deltap3 or deltapx. The opcodes are listed in order of increasing quality which also reflects an increase in computational expense. In the next example a delay tap is inserted within the delay buffer (between the delayr and the delayw) opcodes. As our delay time is modulating quite quickly we will use deltapi which uses linear interpolation as it rebuilds the audio signal whenever the delay time is moving. Note that this time we are not using the audio output from the delayr opcode as we are using the audio output from deltapi instead. The delay time used by deltapi is created by randomi which creates a random function of straight line segments. A-rate is used for the delay time to improve the accuracy of its values, use of k-rate would result in a noticeably poorer sound quality. You will notice that as well as modulating the time gap between echoes, this example also modulates the pitch of the echoes – if the delay tap is static within the buffer there would be no change in pitch, if it is moving towards the beginning of the buffer then pitch will rise and if it is moving towards the end of the buffer then pitch will drop. This side effect has led to digital delay buffers being used in the design of many pitch shifting effects.
The user must take care that the delay time demanded from the delay tap does not exceed the length of the buffer as defined in the delayr line. If it does it will attempt to read data beyond the end of the RAM buffer – the results of this are unpredictable. The user must also take care that the delay time does not go below zero, in fact the minumum delay time that will be permissible will be the duration of one k cycle (ksmps/sr).
EXAMPLE 05D03_deltapi.csd
<CsoundSynthesizer>
<CsOptions>
-odac ; activates real time sound output
</CsOptions>
<CsInstruments>
; Example by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giSine ftgen 0, 0, 2^12, 10, 1 ; a sine wave
instr 1
; -- create an input signal: short 'blip' sounds --
kEnv loopseg 0.5,0,0,0,0.0005,1,0.1,0,1.9,0,0
aEnv interp kEnv
aSig poscil aEnv, 500, giSine
aDelayTime randomi 0.05, 0.2, 1 ; modulating delay time
; -- create a delay buffer --
aBufOut delayr 0.2 ; read audio from end of buffer
aTap deltapi aDelayTime ; 'tap' the delay buffer
delayw aSig + (aTap*0.9) ; write audio into buffer
; send audio to the output (mix the input signal with the delayed signal)
out aSig + (aTap*0.4)
endin
</CsInstruments>
<CsScore>
i 1 0 30
e
</CsScore>
</CsoundSynthesizer>
We are not limited to inserting only a single delay tap within the buffer. If we add further taps we create what is known as a multi-tap delay. The following example implements a multi-tap delay with three delay taps. Note that only the final delay (the one closest to the end of the buffer) is fed back into the input in order to create feedback but all three taps are mixed and sent to the output. There is no reason not to experiment with arrangements other than this, but this one is most typical.
EXAMPLE 05D04_multi-tap_delay.csd
<CsoundSynthesizer>
<CsOptions>
-odac ; activates real time sound output
</CsOptions>
<CsInstruments>
; Example by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giSine ftgen 0, 0, 2^12, 10, 1 ; a sine wave
instr 1
; -- create an input signal: short 'blip' sounds --
kEnv loopseg 0.5,0,0,0,0.0005,1,0.1,0,1.9,0,0; repeating envelope
kCps randomh 400, 1000, 0.5 ; 'held' random values
aEnv interp kEnv ; a-rate envelope
aSig poscil aEnv, kCps, giSine ; generate audio
; -- create a delay buffer --
aBufOut delayr 0.5 ; read audio end buffer
aTap1 deltap 0.1373 ; delay tap 1
aTap2 deltap 0.2197 ; delay tap 2
aTap3 deltap 0.4139 ; delay tap 3
delayw aSig + (aTap3*0.4) ; write audio into buffer
; send audio to the output (mix the input signal with the delayed signals)
out aSig + ((aTap1+aTap2+aTap3)*0.4)
endin
</CsInstruments>
<CsScore>
i 1 0 25
e
</CsScore>
</CsoundSynthesizer>
As mentioned at the top of this section many familiar effects are actually created from using delay buffers in various ways. We will briefly look at one of these effects: the flanger. Flanging derives from a phenomenon which occurs when the delay time becomes so short that we begin to no longer perceive individual echoes. Instead a stack of harmonically related resonances are perceived with frequencies are in simple ratio with 1/delay_time. This effect is known as a comb filter. When the delay time is slowly modulated and the resonances shifting up and down in sympathy the effect becomes known as a flanger. In this example the delay time of the flanger is modulated using an LFO that employs an U-shaped parabola as its waveform as this seems to provide the smoothest comb filter modulations.
EXAMPLE 05D05_flanger.csd
<CsoundSynthesizer>
<CsOptions>
-odac ; activates real time sound output
</CsOptions>
<CsInstruments>
;Example by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giSine ftgen 0, 0, 2^12, 10, 1 ; a sine wave
giLFOShape ftgen 0, 0, 2^12, 19, 0.5, 1, 180, 1 ; u-shaped parabola
instr 1
aSig pinkish 0.1 ; pink noise
aMod poscil 0.005, 0.05, giLFOShape ; delay time LFO
iOffset = ksmps/sr ; minimum delay time
kFdback linseg 0.8,(p3/2)-0.5,0.95,1,-0.95 ; feedback
; -- create a delay buffer --
aBufOut delayr 0.5 ; read audio from end buffer
aTap deltap3 aMod + iOffset ; tap audio from within buffer
delayw aSig + (aTap*kFdback) ; write audio into buffer
; send audio to the output (mix the input signal with the delayed signal)
out aSig + aTap
endin
</CsInstruments>
<CsScore>
i 1 0 25
e
</CsScore>
</CsoundSynthesizer>
Delay buffers can be used to implement a wide variety of signal processing effects beyond simple echo effects. This chapter has introduced the basics of working with Csound's delay opcodes and also hinted at some of the further possibilities available.
REVERBERATION
Reverb is the effect a room or space has on a sound where the sound we perceive is a mixture of the direct sound and the dense overlapping echoes of that sound reflecting off walls and objects within the space.
Csound's earliest reverb opcodes are reverb and nreverb. By today's standards they sound rather crude and as a consequence modern Csound users tend to prefer the more recent opcodes freeverb and reverbsc.
The typical way to use a reverb is to run as a effect throughout the entire Csound performance and to send it audio from other instruments to which it adds reverb. This is more efficient than initiating a new reverb effect for every note that is played. This arrangement is a reflection of how a reverb effect would be used with a mixing desk in a conventional studio. There are several methods of sending audio from sound producing instruments to the reverb instrument, three of which will be introduced in the coming examples
The first method uses Csound's global variables, so that an audio variable created in one instrument and be read in another instrument. There are several points to highlight here. First the global audio variable that is used to send audio to the reverb instrument is initialized to zero (silence) in the header area of the orchestra.
This is done so that if no sound generating instruments are playing at the beginning of the performance this variable still exists and has a value. An error would result otherwise and Csound would not run. When audio is written into this variable in the sound generating instrument it is added to the current value of the global variable.
This is done in order to permit polyphony and so that the state of this variable created by other sound producing instruments is not overwritten. Finally it is important that the global variable is cleared (assigned a value of zero) when it is finished with at the end of the reverb instrument. If this were not done then the variable would quickly 'explode' (get astronomically high) as all previous instruments are merely adding values to it rather that redeclaring it. Clearing could be done simply by setting to zero but the clear opcode might prove useful in the future as it provides us with the opportunity to clear many variables simultaneously.
This example uses the freeverb opcode and is based on a plugin of the same name. Freeverb has a smooth reverberant tail and is perhaps similar in sound to a plate reverb. It provides us with two main parameters of control: 'room size' which is essentially a control of the amount of internal feedback and therefore reverb time, and 'high frequency damping' which controls the amount of attenuation of high frequencies. Both there parameters should be set within the range 0 to 1. For room size a value of zero results in a very short reverb and a value of 1 results in a very long reverb. For high frequency damping a value of zero provides minimum damping of higher frequencies giving the impression of a space with hard walls, a value of 1 provides maximum high frequency damping thereby giving the impression of a space with soft surfaces such as thick carpets and heavy curtains.
EXAMPLE 05E01_freeverb.csd
<CsoundSynthesizer>
<CsOptions>
-odac ; activates real time sound output
</CsOptions>
<CsInstruments>
;Example by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
gaRvbSend init 0 ; global audio variable initialized to zero
instr 1 ; sound generating instrument (sparse noise bursts)
kEnv loopseg 0.5,0,0,1,0.003,1,0.0001,0,0.9969,0,0; amp. env.
aSig pinkish kEnv ; noise pulses
outs aSig, aSig ; audio to outs
iRvbSendAmt = 0.8 ; reverb send amount (0 - 1)
; add some of the audio from this instrument to the global reverb send variable
gaRvbSend = gaRvbSend + (aSig * iRvbSendAmt)
endin
instr 5 ; reverb - always on
kroomsize init 0.85 ; room size (range 0 to 1)
kHFDamp init 0.5 ; high freq. damping (range 0 to 1)
; create reverberated version of input signal (note stereo input and output)
aRvbL,aRvbR freeverb gaRvbSend, gaRvbSend,kroomsize,kHFDamp
outs aRvbL, aRvbR ; send audio to outputs
clear gaRvbSend ; clear global audio variable
endin
</CsInstruments>
<CsScore>
i 1 0 300 ; noise pulses (input sound)
i 5 0 300 ; start reverb
e
</CsScore>
</CsoundSynthesizer>
The next example uses Csound's zak patching system to send audio from one instrument to another. The zak system is a little like a patch bay you might find in a recording studio. Zak channels can be a, k or i-rate. These channels will be addressed using numbers so it will be important to keep track of what each numbered channel is used for. Our example will be very simple in that we will only be using one zak audio channel. Before using any of the zak opcodes for reading and writing data we must initialize zak storage space. This is done in the orchestra header area using the zakinit opcode. This opcode initializes both a and k rate channels; we must intialize at least one of each even if we don't require both.
zakinit 1, 1
The audio from the sound generating instrument is mixed into a zak audio channel the zawm opcode like this:
zawm aSig * iRvbSendAmt, 1
This channel is read from in the reverb instrument using the zar opcode like this:
aInSig zar 1
Because audio is begin mixed into our zak channel but it is never redefined (only mixed into) it needs to be cleared after we have finished with it. This is accomplished at the bottom of the reverb instrument using the zacl opcode like this:
zacl 0, 1
This example uses the reverbsc opcode. It too has a stereo input and output. The arguments that define its character are feedback level and cutoff frequency. Feedback level should be in the range zero to 1 and controls reverb time. Cutoff frequency should be within the range of human hearing (20Hz -20kHz) and less than the Nyqvist frequency (sr/2) - it controls the cutoff frequencies of low pass filters within the algorithm.
EXAMPLE 05E02_reverbsc.csd
<CsoundSynthesizer>
<CsOptions>
-odac ; activates real time sound output
</CsOptions>
<CsInstruments>
; Example by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
; initialize zak space - one a-rate and one k-rate variable.
; We will only be using the a-rate variable.
zakinit 1, 1
instr 1 ; sound generating instrument - sparse noise bursts
kEnv loopseg 0.5,0, 0,1,0.003,1,0.0001,0,0.9969,0,0; amp. env.
aSig pinkish kEnv ; pink noise pulses
outs aSig, aSig ; send audio to outputs
iRvbSendAmt = 0.8 ; reverb send amount (0 - 1)
; write to zak audio channel 1 with mixing
zawm aSig*iRvbSendAmt, 1
endin
instr 5 ; reverb - always on
aInSig zar 1 ; read first zak audio channel
kFblvl init 0.88 ; feedback level - i.e. reverb time
kFco init 8000 ; cutoff freq. of a filter within the reverb
; create reverberated version of input signal (note stereo input and output)
aRvbL,aRvbR reverbsc aInSig, aInSig, kFblvl, kFco
outs aRvbL, aRvbR ; send audio to outputs
zacl 0, 1 ; clear zak audio channels
endin
</CsInstruments>
<CsScore>
i 1 0 10 ; noise pulses (input sound)
i 5 0 12 ; start reverb
e
</CsScore>
</CsoundSynthesizer>
reverbsc contains a mechanism to modulate delay times internally which has the effect of harmonically blurring sounds the longer they are reverberated. This contrasts with freeverb's rather static reverberant tail. On the other hand screverb's tail is not as smooth as that of freeverb, inidividual echoes are sometimes discernible so it may not be as well suited to the reverberation of percussive sounds. Also be aware that as well as reducing the reverb time, the feedback level parameter reduces the overall amplitude of the effect to the point where a setting of 1 will result in silence from the opcode.
A more recent option for sending sound from instrument to instrument in Csound is to use the chn... opcodes. These opcodes can also be used to allow Csound to interface with external programs using the software bus and the Csound API.
EXAMPLE 05E03_reverb_with_chn.csd
<CsoundSynthesizer>
<CsOptions>
-odac ; activates real time sound output
</CsOptions>
<CsInstruments>
; Example by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1 ; sound generating instrument - sparse noise bursts
kEnv loopseg 0.5,0, 0,1,0.003,1,0.0001,0,0.9969,0,0 ; amp. envelope
aSig pinkish kEnv ; noise pulses
outs aSig, aSig ; audio to outs
iRvbSendAmt = 0.4 ; reverb send amount (0 - 1)
;write audio into the named software channel:
chnmix aSig*iRvbSendAmt, "ReverbSend"
endin
instr 5 ; reverb (always on)
aInSig chnget "ReverbSend" ; read audio from the named channel
kTime init 4 ; reverb time
kHDif init 0.5 ; 'high frequency diffusion' (0 - 1)
aRvb nreverb aInSig, kTime, kHDif ; create reverb signal
outs aRvb, aRvb ; send audio to outputs
chnclear "ReverbSend" ; clear the named channel
endin
</CsInstruments>
<CsScore>
i 1 0 10 ; noise pulses (input sound)
i 5 0 12 ; start reverb
e
</CsScore>
</CsoundSynthesizer>
The Schroeder Reverb Design
Many reverb algorithms including Csound's freeverb, reverb and reverbn are based on what is known as the Schroeder reverb design. This was a design proposed in the early 1960s by the physicist Manfred Schroeder. In the Schroeder reverb a signal is passed into four parallel comb filters the outputs of which are summed and then passed through two allpass filters as shown in the diagram below. Essentially the comb filters provide the body of the reverb effect and the allpass filters smear their resultant sound to reduce ringing artefacts the comb filters might produce. More modern designs might extent the number of filters used in an attempt to create smoother results. The freeverb opcode employs eight parallel comb filters followed by four series allpass filters on each channel. The two main indicators of poor implementations of the Schoeder reverb are individual echoes being excessively apparent and ringing artefacts. The results produced by the freeverb opcode are very smooth but a criticism might be that it is lacking in character and is more suggestive of a plate reverb than of a real room.
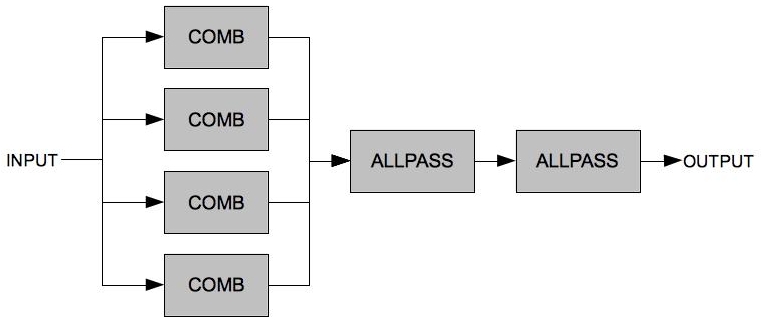
The next example implements the basic Schroeder reverb with four parallel comb filters followed by three series allpass filters. This also proves a useful exercise in routing audio signals within Csound. Perhaps the most crucial element of the Schroeder reverb is the choice of loop times for the comb and allpass filters – careful choices here should obviate the undesirable artefacts mentioned in the previous paragraph. If loop times are too long individual echoes will become apparent, if they are too short the characteristic ringing of comb filters will become apparent. If loop times between filters differ too much the outputs from the various filters will not fuse. It is also important that the loop times are prime numbers so that echoes between different filters do not reinforce each other. It may also be necessary to adjust loop times when implementing very short reverbs or very long reverbs. The duration of the reverb is effectively determined by the reverb times for the comb filters. There is certainly scope for experimentation with the design of this example and exploration of settings other than the ones suggested here.
This example consists of five instruments. The fifth instrument implements the reverb algorithm described above. The first four instruments act as a kind of generative drum machine to provide source material for the reverb. Generally sharp percussive sounds provide the sternest test of a reverb effect. Instrument 1 triggers the various synthesized drum sounds (bass drum, snare and closed hi-hat) produced by instruments 2 to 4.
EXAMPLE 05E04_schroeder_reverb.csd
<CsoundSynthesizer>
<CsOptions>
-odac -m0
; activate real time sound output and suppress note printing
</CsOptions>
<CsInstruments>
;Example by Iain McCurdy
sr = 44100
ksmps = 1
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^12, 10, 1 ; a sine wave
gaRvbSend init 0 ; global audio variable initialized
giRvbSendAmt init 0.4 ; reverb send amount (range 0 - 1)
instr 1 ; trigger drum hits
ktrigger metro 5 ; rate of drum strikes
kdrum random 2, 4.999 ; randomly choose which drum to hit
schedkwhen ktrigger, 0, 0, kdrum, 0, 0.1 ; strike a drum
endin
instr 2 ; sound 1 - bass drum
iamp random 0, 0.5 ; amplitude randomly chosen
p3 = 0.2 ; define duration for this sound
aenv line 1,p3,0.001 ; amplitude envelope (percussive)
icps exprand 30 ; cycles-per-second offset
kcps expon icps+120,p3,20 ; pitch glissando
aSig oscil aenv*0.5*iamp,kcps,giSine ; oscillator
outs aSig, aSig ; send audio to outputs
gaRvbSend = gaRvbSend + (aSig * giRvbSendAmt) ; add to send
endin
instr 3 ; sound 3 - snare
iAmp random 0, 0.5 ; amplitude randomly chosen
p3 = 0.3 ; define duration
aEnv expon 1, p3, 0.001 ; amp. envelope (percussive)
aNse noise 1, 0 ; create noise component
iCps exprand 20 ; cps offset
kCps expon 250 + iCps, p3, 200+iCps ; create tone component gliss.
aJit randomi 0.2, 1.8, 10000 ; jitter on freq.
aTne oscil aEnv, kCps*aJit, giSine ; create tone component
aSig sum aNse*0.1, aTne ; mix noise and tone components
aRes comb aSig, 0.02, 0.0035 ; comb creates a 'ring'
aSig = aRes * aEnv * iAmp ; apply env. and amp. factor
outs aSig, aSig ; send audio to outputs
gaRvbSend = gaRvbSend + (aSig * giRvbSendAmt); add to send
endin
instr 4 ; sound 4 - closed hi-hat
iAmp random 0, 1.5 ; amplitude randomly chosen
p3 = 0.1 ; define duration for this sound
aEnv expon 1,p3,0.001 ; amplitude envelope (percussive)
aSig noise aEnv, 0 ; create sound for closed hi-hat
aSig buthp aSig*0.5*iAmp, 12000 ; highpass filter sound
aSig buthp aSig, 12000 ; -and again to sharpen cutoff
outs aSig, aSig ; send audio to outputs
gaRvbSend = gaRvbSend + (aSig * giRvbSendAmt) ; add to send
endin
instr 5 ; schroeder reverb - always on
; read in variables from the score
kRvt = p4
kMix = p5
; print some information about current settings gleaned from the score
prints "Type:"
prints p6
prints "\\nReverb Time:%2.1f\\nDry/Wet Mix:%2.1f\\n\\n",p4,p5
; four parallel comb filters
a1 comb gaRvbSend, kRvt, 0.0297; comb filter 1
a2 comb gaRvbSend, kRvt, 0.0371; comb filter 2
a3 comb gaRvbSend, kRvt, 0.0411; comb filter 3
a4 comb gaRvbSend, kRvt, 0.0437; comb filter 4
asum sum a1,a2,a3,a4 ; sum (mix) the outputs of all comb filters
; two allpass filters in series
a5 alpass asum, 0.1, 0.005 ; send mix through first allpass filter
aOut alpass a5, 0.1, 0.02291 ; send 1st allpass through 2nd allpass
amix ntrpol gaRvbSend, aOut, kMix ; create a dry/wet mix
outs amix, amix ; send audio to outputs
clear gaRvbSend ; clear global audio variable
endin
</CsInstruments>
<CsScore>
; room reverb
i 1 0 10 ; start drum machine trigger instr
i 5 0 11 1 0.5 "Room Reverb" ; start reverb
; tight ambience
i 1 11 10 ; start drum machine trigger instr
i 5 11 11 0.3 0.9 "Tight Ambience" ; start reverb
; long reverb (low in the mix)
i 1 22 10 ; start drum machine
i 5 22 15 5 0.1 "Long Reverb (Low In the Mix)" ; start reverb
; very long reverb (high in the mix)
i 1 37 10 ; start drum machine
i 5 37 25 8 0.9 "Very Long Reverb (High in the Mix)" ; start reverb
e
</CsScore>
</CsoundSynthesizer>
This chapter has introduced some of the more recent Csound opcodes for delay-line based reverb algorithms which in most situations can be used to provide high quality and efficient reverberation. Convolution offers a whole new approach for the creation of realistic reverbs that imitate actual spaces - this technique is demonstrated in the Convolution chapter.
Csound: AMRMWAVESHAPING
AM / RM / WAVESHAPING
An introduction as well as some background theory of amplitude modulation, ring modulation and waveshaping is given in the fourth chapter entitled "sound-synthesis". As all of these techniques merely modulate the amplitude of a signal in a variety of ways, they can also be used for the modification of non-synthesized sound. In this chapter we will explore amplitude modulation, ring modulation and waveshaping as applied to non-synthesized sound.1
AMPLITUDE MODULATION
With "sound-synthesis", the principle of AM was shown as a amplitude multiplication of two sine oscillators. Later we've used a more complex modulators, to generate more complex spectrums. The principle also works very well with sound-files (samples) or live-audio-input.
Karlheinz Stockhausens "Mixtur für Orchester, vier Sinusgeneratoren und vier Ringmodulatoren” (1964) was the first piece which used analog ringmodulation (AM without DC-offset) to alter the acoustic instruments pitch in realtime during a live-performance. The word ringmodulation inherites from the analog four-diode circuit which was arranged in a "ring".
In the following example shows how this can be done digitally in Csound. In this case a sound-file works as the carrier which is modulated by a sine-wave-osc. The result sounds like old 'Harald Bode' pitch-shifters from the 1960's.
EXAMPLE: 05F01_RM_modification.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 48000
ksmps = 32
nchnls = 1
0dbfs = 1
instr 1 ; Ringmodulation
aSine1 poscil 0.8, p4, 1
aSample diskin2 "fox.wav", 1, 0, 1, 0, 32
out aSine1*aSample
endin
</CsInstruments>
<CsScore>
f 1 0 1024 10 1 ; sine
i 1 0 2 400
i 1 2 2 800
i 1 4 2 1600
i 1 6 2 200
i 1 8 2 2400
e
</CsScore>
</CsoundSynthesizer>
; written by Alex Hofmann (Mar. 2011)
WAVESHAPING
In chapter 04E waveshaping has been described as a method of applying a transfer function to an incoming signal. It has been discussed that the table which stores the transfer function must be read with an interpolating table reader to avoid degradation of the signal. On the other hand, degradation can be a nice thing for sound modification. So let us start with this branch here.
Bit Depth Reduction
If the transfer function itself is linear, but the table of the function is small, and no interpolation is applied to the amplitude as index to the table, in effect the bit depth is reduced. For a function table of size 4, a line becomes a staircase:
Bit Depth = high
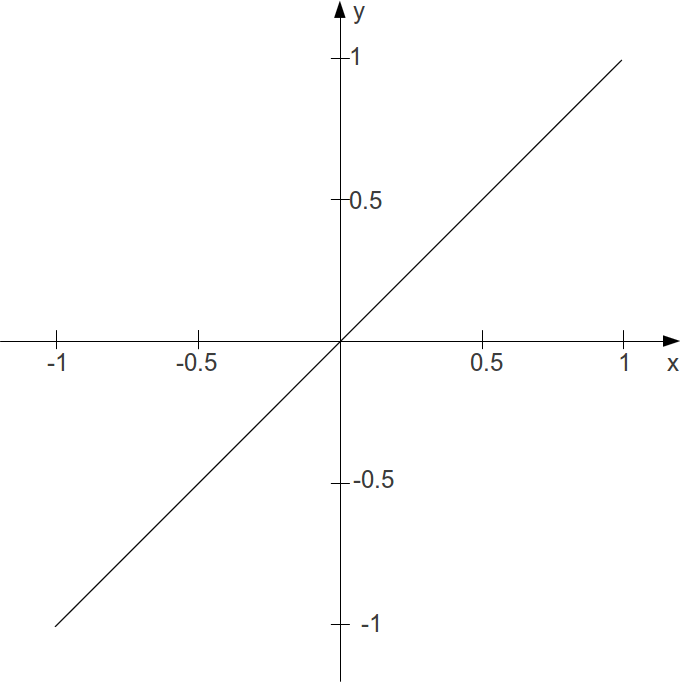
Bit Depth = 2

This is the sounding result:
EXAMPLE 05F02_Wvshp_bit_crunch.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giTrnsFnc ftgen 0, 0, 4, -7, -1, 3, 1
instr 1
aAmp soundin "fox.wav"
aIndx = (aAmp + 1) / 2
aWavShp table aIndx, giTrnsFnc, 1
outs aWavShp, aWavShp
endin
</CsInstruments>
<CsScore>
i 1 0 2.767
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Transformation and Distortion
In general, the transformation of sound in applying waveshaping depends on the transfer function. The following example applies at first a table which does not change the sound at all, because the function just says y = x. The second one leads aready to a heavy distortion, though "just" the samples between an amplitude of -0.1 and +0.1 are erased. Tables 3 to 7 apply some chebychev functions which are well known from waveshaping synthesis. Finally, tables 8 and 9 approve that even a meaningful sentence and a nice music can regarded as noise ...
EXAMPLE 05F03_Wvshp_different_transfer_funs.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giNat ftgen 1, 0, 2049, -7, -1, 2048, 1
giDist ftgen 2, 0, 2049, -7, -1, 1024, -.1, 0, .1, 1024, 1
giCheb1 ftgen 3, 0, 513, 3, -1, 1, 0, 1
giCheb2 ftgen 4, 0, 513, 3, -1, 1, -1, 0, 2
giCheb3 ftgen 5, 0, 513, 3, -1, 1, 0, 3, 0, 4
giCheb4 ftgen 6, 0, 513, 3, -1, 1, 1, 0, 8, 0, 4
giCheb5 ftgen 7, 0, 513, 3, -1, 1, 3, 20, -30, -60, 32, 48
giFox ftgen 8, 0, -121569, 1, "fox.wav", 0, 0, 1
giGuit ftgen 9, 0, -235612, 1, "ClassGuit.wav", 0, 0, 1
instr 1
iTrnsFnc = p4
kEnv linseg 0, .01, 1, p3-.2, 1, .01, 0
aL, aR soundin "ClassGuit.wav"
aIndxL = (aL + 1) / 2
aWavShpL tablei aIndxL, iTrnsFnc, 1
aIndxR = (aR + 1) / 2
aWavShpR tablei aIndxR, iTrnsFnc, 1
outs aWavShpL*kEnv, aWavShpR*kEnv
endin
</CsInstruments>
<CsScore>
i 1 0 7 1 ;natural though waveshaping
i 1 + . 2 ;rather heavy distortion
i 1 + . 3 ;chebychev for 1st partial
i 1 + . 4 ;chebychev for 2nd partial
i 1 + . 5 ;chebychev for 3rd partial
i 1 + . 6 ;chebychev for 4th partial
i 1 + . 7 ;after dodge/jerse p.136
i 1 + . 8 ;fox
i 1 + . 9 ;guitar
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Instead of using the "self-built" method which has been described here, you can use the Csound opcode distort. It performs the actual waveshaping process and gives a nice control about the amount of distortion in the kdist parameter. Here is a simple example:2
EXAMPLE 05F04_distort.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
gi1 ftgen 1,0,257,9,.5,1,270 ;sinoid (also the next)
gi2 ftgen 2,0,257,9,.5,1,270,1.5,.33,90,2.5,.2,270,3.5,.143,90
gi3 ftgen 3,0,129,7,-1,128,1 ;actually natural
gi4 ftgen 4,0,129,10,1 ;sine
gi5 ftgen 5,0,129,10,1,0,1,0,1,0,1,0,1 ;odd partials
gi6 ftgen 6,0,129,21,1 ;white noise
gi7 ftgen 7,0,129,9,.5,1,0 ;half sine
gi8 ftgen 8,0,129,7,1,64,1,0,-1,64,-1 ;square wave
instr 1
ifn = p4
ivol = p5
kdist line 0, p3, 1 ;increase the distortion over p3
aL, aR soundin "ClassGuit.wav"
aout1 distort aL, kdist, ifn
aout2 distort aR, kdist, ifn
outs aout1*ivol, aout2*ivol
endin
</CsInstruments>
<CsScore>
i 1 0 7 1 1
i . + . 2 .3
i . + . 3 1
i . + . 4 .5
i . + . 5 .15
i . + . 6 .04
i . + . 7 .02
i . + . 8 .02
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
- This is the same for Granular Synthesis which can either be "pure" synthesis or applied so sampled sound.^
- Have a look at Iain McCurdy's Realtime example (which has also been ported to CsoundQt by René Jopi) for 'distort' for a more interactive exploration of the opcode.^
GRANULAR SYNTHESIS
This chapter will focus upon granular synthesis used as a DSP technique upon recorded sound files and will introduce techniques including time stretching, time compressing and pitch shifting. The emphasis will be upon asynchronous granulation. For an introduction to synchronous granular synthesis using simple waveforms please refer to chapter 04F.
Csound offers a wide range of opcodes for sound granulation. Each has its own strengths and weaknesses and suitability for a particular task. Some are easier to use than others, some, such as granule and partikkel, are extremely complex and are, at least in terms of the number of input arguments they demand, amongst Csound's most complex opcodes.
sndwarp - Time Stretching and Pitch Shifting
sndwarp may not be Csound's newest or most advanced opcode for sound granulation but it is quite easy to use and is certainly up to the task of time stretching and pitch shifting. sndwarp has two modes by which we can modulate time stretching characteristics, one in which we define a 'stretch factor', a value of 2 defining a stretch to twice the normal length, and the other in which we directly control a pointer into the file. The following example uses sndwarp's first mode to produce a sequence of time stretches and pitch shifts. An overview of each procedure will be printed to the terminal as it occurs. sndwarp does not allow for k-rate modulation of grain size or density so for this level we need to look elsewhere.
You will need to make sure that a sound file is available to sndwarp via a GEN01 function table. You can replace the one used in this example with one of your own by replacing the reference to 'ClassicalGuitar.wav'. This sound file is stereo therefore instrument 1 uses the stereo version 'sndwarpst'. A mismatch between the number of channels in the sound file and the version of sndwarp used will result in playback at an unexpected pitch. You will also need to give GEN01 an appropriate size that will be able to contain your chosen sound file. You can calculate the table size you will need by multiplying the duration of the sound file (in seconds) by the sample rate - for stereo files this value should be doubled - and then choose the next power of 2 above this value. You can download the sample used in the example at http://www.iainmccurdy.org/csoundrealtimeexamples/sourcematerials/ClassicalGuitar.wav.
sndwarp describes grain size as 'window size' and it is defined in samples so therefore a window size of 44100 means that grains will last for 1s each (when sample rate is set at 44100). Window size randomization (irandw) adds a random number within that range to the duration of each grain. As these two parameters are closely related it is sometime useful to set irandw to be a fraction of window size. If irandw is set to zero we will get artefacts associated with synchronous granular synthesis.
sndwarp (along with many of Csound's other granular synthesis opcodes) requires us to supply it with a window function in the form of a function table according to which it will apply an amplitude envelope to each grain. By using different function tables we can alternatively create softer grains with gradual attacks and decays (as in this example), with more of a percussive character (short attack, long decay) or 'gate'-like (short attack, long sustain, short decay).
EXAMPLE 05G01_sndwarp.csd
<CsoundSynthesizer>
<CsOptions>
-odac -m0
; activate real-time audio output and suppress printing
</CsOptions>
<CsInstruments>
; example written by Iain McCurdy
sr = 44100
ksmps = 16
nchnls = 2
0dbfs = 1
; waveform used for granulation
giSound ftgen 1,0,2097152,1,"ClassGuit.wav",0,0,0
; window function - used as an amplitude envelope for each grain
; (first half of a sine wave)
giWFn ftgen 2,0,16384,9,0.5,1,0
instr 1
kamp = 0.1
ktimewarp expon p4,p3,p5 ; amount of time stretch, 1=none 2=double
kresample line p6,p3,p7 ; pitch change 1=none 2=+1oct
ifn1 = giSound ; sound file to be granulated
ifn2 = giWFn ; window shaped used to envelope every grain
ibeg = 0
iwsize = 3000 ; grain size (in sample)
irandw = 3000 ; randomization of grain size range
ioverlap = 50 ; density
itimemode = 0 ; 0=stretch factor 1=pointer
prints p8 ; print a description
aSigL,aSigR sndwarpst kamp,ktimewarp,kresample,ifn1,ibeg, \
iwsize,irandw,ioverlap,ifn2,itimemode
outs aSigL,aSigR
endin
</CsInstruments>
<CsScore>
;p3 = stretch factor begin / pointer location begin
;p4 = stretch factor end / pointer location end
;p5 = resample begin (transposition)
;p6 = resample end (transposition)
;p7 = procedure description
;p8 = description string
; p1 p2 p3 p4 p5 p6 p7 p8
i 1 0 10 1 1 1 1 "No time stretch. No pitch shift."
i 1 10.5 10 2 2 1 1 "%nTime stretch x 2."
i 1 21 20 1 20 1 1 \
"%nGradually increasing time stretch factor from x 1 to x 20."
i 1 41.5 10 1 1 2 2 "%nPitch shift x 2 (up 1 octave)."
i 1 52 10 1 1 0.5 0.5 "%nPitch shift x 0.5 (down 1 octave)."
i 1 62.5 10 1 1 4 0.25 \
"%nPitch shift glides smoothly from 4 (up 2 octaves) to 0.25 (down 2 octaves)."
i 1 73 15 4 4 1 1 \
"%nA chord containing three transpositions: unison, +5th, +10th. (x4 time stretch.)"
i 1 73 15 4 4 [3/2] [3/2] ""
i 1 73 15 4 4 3 3 ""
e
</CsScore>
</CsoundSynthesizer>
The next example uses sndwarp's other timestretch mode with which we explicitly define a pointer position from where in the source file grains shall begin. This method allows us much greater freedom with how a sound will be time warped; we can even freeze movement and go backwards in time - something that is not possible with timestretching mode.
This example is self generative in that instrument 2, the instrument that actually creates the granular synthesis textures, is repeatedly triggered by instrument 1. Instrument 2 is triggered once every 12.5s and these notes then last for 40s each so will overlap. Instrument 1 is played from the score for 1 hour so this entire process will last that length of time. Many of the parameters of granulation are chosen randomly when a note begins so that each note will have unique characteristics. The timestretch is created by a line function: the start and end points of which are defined randomly when the note begins. Grain/window size and window size randomization are defined randomly when a note begins - notes with smaller window sizes will have a fuzzy airy quality wheres notes with a larger window size will produce a clearer tone. Each note will be randomly transposed (within a range of +/- 2 octaves) but that transposition will be quantized to a rounded number of semitones - this is done as a response to the equally tempered nature of source sound material used.
Each entire note is enveloped by an amplitude envelope and a resonant lowpass filter in each case encasing each note under a smooth arc. Finally a small amount of reverb is added to smooth the overall texture slightly
EXAMPLE 05G02_selfmade_grain.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;example written by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
; the name of the sound file used is defined as a string variable -
; - as it will be used twice in the code.
; This simplifies adapting the orchestra to use a different sound file
gSfile = "ClassGuit.wav"
; waveform used for granulation
giSound ftgen 1,0,2097152,1,gSfile,0,0,0
; window function - used as an amplitude envelope for each grain
giWFn ftgen 2,0,16384,9,0.5,1,0
seed 0 ; seed the random generators from the system clock
gaSendL init 0 ; initialize global audio variables
gaSendR init 0
instr 1 ; triggers instrument 2
ktrigger metro 0.08 ;metronome of triggers. One every 12.5s
schedkwhen ktrigger,0,0,2,0,40 ;trigger instr. 2 for 40s
endin
instr 2 ; generates granular synthesis textures
;define the input variables
ifn1 = giSound
ilen = nsamp(ifn1)/sr
iPtrStart random 1,ilen-1
iPtrTrav random -1,1
ktimewarp line iPtrStart,p3,iPtrStart+iPtrTrav
kamp linseg 0,p3/2,0.2,p3/2,0
iresample random -24,24.99
iresample = semitone(int(iresample))
ifn2 = giWFn
ibeg = 0
iwsize random 400,10000
irandw = iwsize/3
ioverlap = 50
itimemode = 1
; create a stereo granular synthesis texture using sndwarp
aSigL,aSigR sndwarpst kamp,ktimewarp,iresample,ifn1,ibeg,\
iwsize,irandw,ioverlap,ifn2,itimemode
; envelope the signal with a lowpass filter
kcf expseg 50,p3/2,12000,p3/2,50
aSigL moogvcf2 aSigL, kcf, 0.5
aSigR moogvcf2 aSigR, kcf, 0.5
; add a little of our audio signals to the global send variables -
; - these will be sent to the reverb instrument (2)
gaSendL = gaSendL+(aSigL*0.4)
gaSendR = gaSendR+(aSigR*0.4)
outs aSigL,aSigR
endin
instr 3 ; reverb (always on)
aRvbL,aRvbR reverbsc gaSendL,gaSendR,0.85,8000
outs aRvbL,aRvbR
;clear variables to prevent out of control accumulation
clear gaSendL,gaSendR
endin
</CsInstruments>
<CsScore>
; p1 p2 p3
i 1 0 3600 ; triggers instr 2
i 3 0 3600 ; reverb instrument
e
</CsScore>
</CsoundSynthesizer>
granule - Clouds of Sound
The granule opcode is one of Csound's most complex opcodes requiring up to 22 input arguments in order to function. Only a few of these arguments are available during performance (k-rate) so it is less well suited for real-time modulation, for real-time a more nimble implementation such as syncgrain, fog, or grain3 would be recommended. For more complex realtime granular techniques, the partikkel opcode can be used. The granule opcode as used here, proves itself ideally suited at the production of massive clouds of granulated sound in which individual grains are often completely indistinguishable. There are still two important k-rate variables that have a powerful effect on the texture created when they are modulated during a note, they are: grain gap - effectively density - and grain size which will affect the clarity of the texture - textures with smaller grains will sound fuzzier and airier, textures with larger grains will sound clearer. In the following example transeg envelopes move the grain gap and grain size parameters through a variety of different states across the duration of each note.
With granule we define a number a grain streams for the opcode using its 'ivoice' input argument. This will also have an effect on the density of the texture produced. Like sndwarp's first timestretching mode, granule also has a stretch ratio parameter. Confusingly it works the other way around though, a value of 0.5 will slow movement through the file by 1/2, 2 will double is and so on. Increasing grain gap will also slow progress through the sound file. granule also provides up to four pitch shift voices so that we can create chord-like structures without having to use more than one iteration of the opcode. We define the number of pitch shifting voices we would like to use using the 'ipshift' parameter. If this is given a value of zero, all pitch shifting intervals will be ignored and grain-by-grain transpositions will be chosen randomly within the range +/-1 octave. granule contains built-in randomizing for several of it parameters in order to easier facilitate asynchronous granular synthesis. In the case of grain gap and grain size randomization these are defined as percentages by which to randomize the fixed values.
Unlike Csound's other granular synthesis opcodes, granule does not use a function table to define the amplitude envelope for each grain, instead attack and decay times are defined as percentages of the total grain duration using input arguments. The sum of these two values should total less than 100.
Five notes are played by this example. While each note explores grain gap and grain size in the same way each time, different permutations for the four pitch transpositions are explored in each note. Information about what these transpositions are, are printed to the terminal as each note begins.
EXAMPLE 05G03_granule.csd
<CsoundSynthesizer>
<CsOptions>
-odac -m0
; activate real-time audio output and suppress note printing
</CsOptions>
<CsInstruments>
; example written by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
;waveforms used for granulation
giSoundL ftgen 1,0,1048576,1,"ClassGuit.wav",0,0,1
giSoundR ftgen 2,0,1048576,1,"ClassGuit.wav",0,0,2
seed 0; seed the random generators from the system clock
gaSendL init 0
gaSendR init 0
instr 1 ; generates granular synthesis textures
prints p9
;define the input variables
kamp linseg 0,1,0.1,p3-1.2,0.1,0.2,0
ivoice = 64
iratio = 0.5
imode = 1
ithd = 0
ipshift = p8
igskip = 0.1
igskip_os = 0.5
ilength = nsamp(giSoundL)/sr
kgap transeg 0,20,14,4, 5,8,8, 8,-10,0, 15,0,0.1
igap_os = 50
kgsize transeg 0.04,20,0,0.04, 5,-4,0.01, 8,0,0.01, 15,5,0.4
igsize_os = 50
iatt = 30
idec = 30
iseedL = 0
iseedR = 0.21768
ipitch1 = p4
ipitch2 = p5
ipitch3 = p6
ipitch4 = p7
;create the granular synthesis textures; one for each channel
aSigL granule kamp,ivoice,iratio,imode,ithd,giSoundL,ipshift,igskip,\
igskip_os,ilength,kgap,igap_os,kgsize,igsize_os,iatt,idec,iseedL,\
ipitch1,ipitch2,ipitch3,ipitch4
aSigR granule kamp,ivoice,iratio,imode,ithd,giSoundR,ipshift,igskip,\
igskip_os,ilength,kgap,igap_os,kgsize,igsize_os,iatt,idec,iseedR,\
ipitch1,ipitch2,ipitch3,ipitch4
;send a little to the reverb effect
gaSendL = gaSendL+(aSigL*0.3)
gaSendR = gaSendR+(aSigR*0.3)
outs aSigL,aSigR
endin
instr 2 ; global reverb instrument (always on)
; use reverbsc opcode for creating reverb signal
aRvbL,aRvbR reverbsc gaSendL,gaSendR,0.85,8000
outs aRvbL,aRvbR
;clear variables to prevent out of control accumulation
clear gaSendL,gaSendR
endin
</CsInstruments>
<CsScore>
; p4 = pitch 1
; p5 = pitch 2
; p6 = pitch 3
; p7 = pitch 4
; p8 = number of pitch shift voices (0=random pitch)
; p1 p2 p3 p4 p5 p6 p7 p8 p9
i 1 0 48 1 1 1 1 4 "pitches: all unison"
i 1 + . 1 0.5 0.25 2 4 \
"%npitches: 1(unison) 0.5(down 1 octave) 0.25(down 2 octaves) 2(up 1 octave)"
i 1 + . 1 2 4 8 4 "%npitches: 1 2 4 8"
i 1 + . 1 [3/4] [5/6] [4/3] 4 "%npitches: 1 3/4 5/6 4/3"
i 1 + . 1 1 1 1 0 "%npitches: all random"
i 2 0 [48*5+2]; reverb instrument
e
</CsScore>
</CsoundSynthesizer>
Grain delay effect
Granular techniques can be used to implement a flexible delay effect, where we can do transposition, time modification and disintegration of the sound into small particles, all within the delay effect itself. To implement this effect, we record live audio into a buffer (Csound table), and let the granular synthesizer/generator read sound for the grains from this buffer. We need a granular synthesizer that allows manual control over the read start point for each grain, since the relationship between the write position and the read position in the buffer determines the delay time. We've used the fof2 opcode for this purpose here.
EXAMPLE 05G04_grain_delay.csd
<CsoundSynthesizer>
<CsOptions>
; activate real-time audio output and suppress note printing
-odac -d -m128
</CsOptions>
<CsInstruments>
;example by Oeyvind Brandtsegg
sr = 44100
ksmps = 512
nchnls = 2
0dbfs = 1
; empty table, live audio input buffer used for granulation
giTablen = 131072
giLive ftgen 0,0,giTablen,2,0
; sigmoid rise/decay shape for fof2, half cycle from bottom to top
giSigRise ftgen 0,0,8192,19,0.5,1,270,1
; test sound
giSample ftgen 0,0,524288,1,"fox.wav", 0,0,0
instr 1
; test sound, replace with live input
a1 loscil 1, 1, giSample, 1
outch 1, a1
chnmix a1, "liveAudio"
endin
instr 2
; write live input to buffer (table)
a1 chnget "liveAudio"
gkstart tablewa giLive, a1, 0
if gkstart < giTablen goto end
gkstart = 0
end:
a0 = 0
chnset a0, "liveAudio"
endin
instr 3
; delay parameters
kDelTim = 0.5 ; delay time in seconds (max 2.8 seconds)
kFeed = 0.8
; delay time random dev
kTmod = 0.2
kTmod rnd31 kTmod, 1
kDelTim = kDelTim+kTmod
; delay pitch random dev
kFmod linseg 0, 1, 0, 1, 0.1, 2, 0, 1, 0
kFmod rnd31 kFmod, 1
; grain delay processing
kamp = ampdbfs(-8)
kfund = 25 ; grain rate
kform = (1+kFmod)*(sr/giTablen) ; grain pitch transposition
koct = 0
kband = 0
kdur = 2.5 / kfund ; duration relative to grain rate
kris = 0.5*kdur
kdec = 0.5*kdur
kphs = (gkstart/giTablen)-(kDelTim/(giTablen/sr)) ; calculate grain phase based on delay time
kgliss = 0
a1 fof2 1, kfund, kform, koct, kband, kris, kdur, kdec, 100, \
giLive, giSigRise, 86400, kphs, kgliss
outch 2, a1*kamp
chnset a1*kFeed, "liveAudio"
endin
</CsInstruments>
<CsScore>
i 1 0 20
i 2 0 20
i 3 0 20
e
</CsScore>
</CsoundSynthesizer>
In the last example we will use the grain opcode. This opcode is part of a little group of opcodes which also includes grain2 and grain3. Grain is the oldest opcode, Grain2 is a more easy-to-use opcode, while Grain3 offers more control.
EXAMPLE 05G05_grain.csd
<CsoundSynthesizer>
<CsOptions>
-o dac -d
</CsOptions>
<CsInstruments>
; Example by Bjørn Houdorf, february 2013
sr = 44100
ksmps = 128
nchnls = 2
0dbfs = 1
; First we hear each grain, but later on it sounds more like a drum roll.
; If your computer have problems with running this CSD-file in real-time,
; you can render to a soundfile. Just write "-o filename" in the <CsOptions>,
; instead of "-o dac"
gareverbL init 0
gareverbR init 0
giFt1 ftgen 0, 0, 1025, 20, 2, 1 ; GEN20, Hanning window for grain envelope
; The soundfile(s) you use should be in the same folder as your csd-file
; The soundfile "fox.wav" can be downloaded at http://csound-tutorial.net/node/1/58
giFt2 ftgen 0, 0, 524288, 1, "fox.wav", 0, 0, 0
; Instead you can use your own soundfile(s)
instr 1 ; Granular synthesis of soundfile
ipitch = sr/ftlen(giFt2) ; Original frequency of the input sound
kdens1 expon 3, p3, 500
kdens2 expon 4, p3, 400
kdens3 expon 5, p3, 300
kamp line 1, p3, 0.05
a1 grain 1, ipitch, kdens1, 0, 0, 1, giFt2, giFt1, 1
a2 grain 1, ipitch, kdens2, 0, 0, 1, giFt2, giFt1, 1
a3 grain 1, ipitch, kdens3, 0, 0, 1, giFt2, giFt1, 1
aleft = kamp*(a1+a2)
aright = kamp*(a2+a3)
outs aleft, aright ; Output granulation
gareverbL = gareverbL + a1+a2 ; send granulation to Instr 2 (Reverb)
gareverbR = gareverbR + a2+a3
endin
instr 2 ; Reverb
kkamp line 0, p3, 0.08
aL reverb gareverbL, 10*kkamp ; reverberate what is in gareverbL
aR reverb gareverbR, 10*kkamp ; and garaverbR
outs kkamp*aL, kkamp*aR ; and output the result
gareverbL = 0 ; empty the receivers for the next loop
gareverbR = 0
endin
</CsInstruments>
<CsScore>
i1 0 20 ; Granulation
i2 0 21 ; Reverb
</CsScore>
</CsoundSynthesizer>
Conclusion
Several opcodes for granular synthesis have been considered in this chapter but this is in no way meant to suggest that these are the best, in fact it is strongly recommended to explore all of Csound's other opcodes as they each have their own unique character. The syncgrain family of opcodes (including also syncloop and diskgrain) are deceptively simple as their k-rate controls encourages further abstractions of grain manipulation, fog is designed for FOF synthesis type synchronous granulation but with sound files and partikkel offers a comprehensive control of grain characteristics on a grain-by-grain basis inspired by Curtis Roads' encyclopedic book on granular synthesis 'Microsound'.
CONVOLUTION
Convolution is a mathematical procedure whereby one function is modified by another. Applied to audio, one of these functions might be a sound file or a stream of live audio whilst the other will be, what is referred to as, an impulse response file; this could actually just be another shorter sound file. The longer sound file or live audio stream will be modified by the impulse response so that the sound file will be imbued with certain qualities of the impulse response. It is important to be aware that convolution is a far from trivial process and that realtime performance may be a frequent consideration. Effectively every sample in the sound file to be processed will be multiplied in turn by every sample contained within the impulse response file. Therefore, for a 1 second impulse response at a sampling frequency of 44100 hertz, each and every sample of the input sound file or sound stream will undergo 44100 multiplication operations. Expanding upon this even further, for 1 second's worth of a convolution procedure this will result in 44100 x 44100 (or 1,944,810,000) multiplications. This should provide some insight into the processing demands of a convolution procedure and also draw attention to the efficiency cost of using longer impulse response files.
The most common application of convolution in audio processing is reverberation but convolution is equally adept at, for example, imitating the filtering and time smearing characteristics of vintage microphones, valve amplifiers and speakers. It is also used sometimes to create more unusual special effects. The strength of convolution based reverbs is that they implement acoustic imitations of actual spaces based upon 'recordings' of those spaces. All the quirks and nuances of the original space will be retained. Reverberation algorithms based upon networks of comb and allpass filters create only idealised reverb responses imitating spaces that don't actually exist. The impulse response is a little like a 'fingerprint' of the space. It is perhaps easier to manipulate characteristics such as reverb time and high frequency diffusion (i.e. lowpass filtering) of the reverb effect when using a Schroeder derived algorithm using comb and allpass filters but most of these modification are still possible, if not immediately apparent, when implementing reverb using convolution. The quality of a convolution reverb is largely dependent upon the quality of the impulse response used. An impulse response recording is typically achieved by recording the reverberant tail that follows a burst of white noise. People often employ techniques such as bursting balloons to achieve something approaching a short burst of noise. Crucially the impulse sound should not excessively favour any particular frequency or exhibit any sort of resonance. More modern techniques employ a sine wave sweep through all the audible frequencies when recording an impulse response. Recorded results using this technique will normally require further processing in order to provide a usable impulse response file and this approach will normally be beyond the means of a beginner.
Many commercial, often expensive, implementations of convolution exist both in the form of software and hardware but fortunately Csound provides easy access to convolution for free. Csound currently lists six different opcodes for convolution, convolve (convle), cross2, dconv, ftconv, ftmorf and pconvolve. convolve (convle) and dconv are earlier implementations and are less suited to realtime operation, cross2 relates to FFT-based cross synthesis and ftmorf is used to morph between similar sized function table and is less related to what has been discussed so far, therefore in this chapter we shall focus upon just two opcodes, pconvolve and ftconv.
pconvolve
pconvolve is perhaps the easiest of Csound's convolution opcodes to use and the most useful in a realtime application. It uses the uniformly partitioned (hence the 'p') overlap-save algorithm which permits convolution with very little delay (latency) in the output signal. The impulse response file that it uses is referenced directly, i.e. it does not have to be previously loaded into a function table, and multichannel files are permitted. The impulse response file can be any standard sound file acceptable to Csound and does not need to be pre-analysed as is required by convolve. Convolution procedures through their very nature introduce a delay in the output signal but pconvolve minimises this using the algorithm mentioned above. It will still introduce some delay but we can control this using the opcode's 'ipartitionsize' input argument. What value we give this will require some consideration and perhaps some experimentation as choosing a high partition size will result in excessively long delays (only an issue in realtime work) whereas very low partition sizes demand more from the CPU and too low a size may result in buffer under-runs and interrupted realtime audio. Bear in mind still that realtime CPU performance will depend heavily on the length of the impulse file. The partition size argument is actually an optional argument and if omitted it will default to whatever the software buffer size is as defined by the -b command line flag. If we specify the partition size explicitly however, we can use this information to delay the input audio (after it has been used by pconvolve) so that it can be realigned in time with the latency affected audio output from pconvolve - this will be essential in creating a 'wet/dry' mix in a reverb effect. Partition size is defined in sample frames therefore if we specify a partition size of 512, the delay resulting from the convolution procedure will be 512/sr (sample rate).
In the following example a monophonic drum loop sample undergoes processing through a convolution reverb implemented using pconvolve which in turn uses two different impulse files. The first file is a more conventional reverb impulse file taken in a stairwell whereas the second is a recording of the resonance created by striking a terracota bowl sharply. If you wish to use the three sound files I have used in creating this example, the mono input sound file is here and the two stereo sound files used as impulse responses are here and here. You can, of course, replace them with ones of your own but remain mindful of mono/stereo/multichannel integrity.
EXAMPLE 05H01_pconvolve.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 512
nchnls = 2
0dbfs = 1
gasig init 0
instr 1 ; sound file player
gasig diskin2 p4,1,0,1
endin
instr 2 ; convolution reverb
; Define partion size.
; Larger values require less CPU but result in more latency.
; Smaller values produce lower latency but may cause -
; - realtime performance issues
ipartitionsize = 256
ar1,ar2 pconvolve gasig, p4,ipartitionsize
; create a delayed version of the input signal that will sync -
; - with convolution output
adel delay gasig,ipartitionsize/sr
; create a dry/wet mix
aMixL ntrpol adel,ar1*0.1,p5
aMixR ntrpol adel,ar2*0.1,p5
outs aMixL,aMixR
gasig = 0
endin
</CsInstruments>
<CsScore>
; instr 1. sound file player
; p4=input soundfile
; instr 2. convolution reverb
; p4=impulse response file
; p5=dry/wet mix (0 - 1)
i 1 0 8.6 "loop.wav"
i 2 0 10 "Stairwell.wav" 0.3
i 1 10 8.6 "loop.wav"
i 2 10 10 "Dish.wav" 0.8
e
</CsScore>
</CsoundSynthesizer>
ftconv
ftconv (abbreviated from 'function table convolution) is perhaps slightly more complicated to use than pconvolve but offers additional options. The fact that ftconv utilises an impulse response that we must first store in a function table rather than directly referencing a sound file stored on disk means that we have the option of performing transformations upon the audio stored in the function table before it is employed by ftconv for convolution. This example begins just as the previous example: a mono drum loop sample is convolved first with a typical reverb impulse response and then with an impulse response derived from a terracotta bowl. After twenty seconds the contents of the function tables containing the two impulse responses are reversed by calling a UDO (instrument 3) and the convolution procedure is repeated, this time with a 'backwards reverb' effect. When the reversed version is performed the dry signal is delayed further before being sent to the speakers so that it appears that the reverb impulse sound occurs at the culmination of the reverb build-up. This additional delay is switched on or off via p6 from the score. As with pconvolve, ftconv performs the convolution process in overlapping partitions to minimise latency. Again we can minimise the size of these partitions and therefore the latency but at the cost of CPU efficiency. ftconv's documentation refers to this partition size as 'iplen' (partition length). ftconv offers further facilities to work with multichannel files beyond stereo. When doing this it is suggested that you use GEN52 which is designed for this purpose. GEN01 seems to work fine, at least up to stereo, provided that you do not defer the table size definition (size=0). With ftconv we can specify the actual length of the impulse response - it will probably be shorter than the power-of-2 sized function table used to store it - and this action will improve realtime efficiency. This optional argument is defined in sample frames and defaults to the size of the impulse response function table.
EXAMPLE 05H02_ftconv.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 512
nchnls = 2
0dbfs = 1
; impulse responses stored as stereo GEN01 function tables
giStairwell ftgen 1,0,131072,1,"Stairwell.wav",0,0,0
giDish ftgen 2,0,131072,1,"Dish.wav",0,0,0
gasig init 0
; reverse function table UDO
opcode tab_reverse,0,i
ifn xin
iTabLen = ftlen(ifn)
iTableBuffer ftgentmp 0,0,-iTabLen,-2, 0
icount = 0
loop:
ival table iTabLen-icount-1, ifn
tableiw ival,icount,iTableBuffer
loop_lt icount,1,iTabLen,loop
icount = 0
loop2:
ival table icount,iTableBuffer
tableiw ival,icount,ifn
loop_lt icount,1,iTabLen,loop2
endop
instr 3 ; reverse the contents of a function table
tab_reverse p4
endin
instr 1 ; sound file player
gasig diskin2 p4,1,0,1
endin
instr 2 ; convolution reverb
; buffer length
iplen = 1024
; derive the length of the impulse response
iirlen = nsamp(p4)
ar1,ar2 ftconv gasig, p4, iplen,0, iirlen
; delay compensation. Add extra delay if reverse reverb is used.
adel delay gasig,(iplen/sr) + ((iirlen/sr)*p6)
; create a dry/wet mix
aMixL ntrpol adel,ar1*0.1,p5
aMixR ntrpol adel,ar2*0.1,p5
outs aMixL,aMixR
gasig = 0
endin
</CsInstruments>
<CsScore>
; instr 1. sound file player
; p4=input soundfile
; instr 2. convolution reverb
; p4=impulse response file
; p5=dry/wet mix (0 - 1)
; p6=reverse reverb switch (0=off,1=on)
; instr 3. reverse table contents
; p4=function table number
; 'stairwell' impulse response
i 1 0 8.5 "loop.wav"
i 2 0 10 1 0.3 0
; 'dish' impulse response
i 1 10 8.5 "loop.wav"
i 2 10 10 2 0.8 0
; reverse the impulse responses
i 3 20 0 1
i 3 20 0 2
; 'stairwell' impulse response (reversed)
i 1 21 8.5 "loop.wav"
i 2 21 10 1 0.5 1
; 'dish' impulse response (reversed)
i 1 31 8.5 "loop.wav"
i 2 31 10 2 0.5 1
e
</CsScore>
</CsoundSynthesizer
Suggested avenues for further exploration with ftconv could be applying envelopes to, filtering and time stretching and compressing the function table stored impulse files before use in convolution.
The impulse responses I have used here are admittedly of rather low quality and whilst it is always recommended to maintain as high standards of sound quality as possible the user should not feel restricted from exploring the sound transformation possibilities possible form whatever source material they may have lying around. Many commercial convolution algorithms demand a proprietary impulse response format inevitably limiting the user to using the impulse responses provided by the software manufacturers but with Csound we have the freedom to use any sound we like.
Csound: FOURIERSPECTRAL
FOURIER TRANSFORMATION / SPECTRAL PROCESSING
A Fourier Transformation (FT) is used to transfer an audio-signal from the time-domain to the frequency-domain. This can, for instance, be used to analyze and visualize the spectrum of the signal appearing in a certain time span. Fourier transform and subsequent manipulations in the frequency domain open a wide area of interesting sound transformations, like time stretching, pitch shifting and much more.
How does it work?
The mathematician J.B. Fourier (1768-1830) developed a method to approximate periodic functions by using sums of trigonometric functions. The advantage of this was that the properties of the trigonometric functions (sin & cos) were well-known and helped to describe the properties of the unknown function.
In audio DSP, a fourier transformed signal is decomposed into its sum of sinoids. Put simply, Fourier transform is the opposite of additive synthesis. Ideally, a sound can be dissected by Fourier transformation into its partial components, and resynthesized again by adding these components back together again.
On account of the fact that sound is represented as discrete samples in the computer, the computer implementation of the FT calculates a discrete Fourier transform (DFT). As each transformation needs a certain number of samples, one key decision in performing DFT is about the number of samples used. The analysis of the frequency components will be more accurate if more samples are used, but as samples represent a progression of time, a caveat must be found for each FT between either better time resolution (fewer samples) or better frequency resolution (more samples). A typical value for FT in music is to have about 20-100 "snapshots" per second (which can be compared to the single frames in a film or video).
At a sample rate of 48000 samples per second, these are about 500-2500 samples for one frame or window. It is normal in DFT in computer music to use window sizes which are a power-of-two in size, such as 512, 1024 or 2048 samples. The reason for this restriction is that DFT for these power-of-two sized frames can be calculated much faster. This is called Fast Fourier Transform (FFT), and this is the standard implementation of the Fourier transform in audio applications.
How is FFT done in Csound?
As usual, there is not just one way to work with FFT and spectral processing in Csound. There are several families of opcodes. Each family can be very useful for a specific approach to working in the frequency domain. Have a look at the "Spectral Processing" overview in the Csound Manual. This introduction will focus on the so-called "Phase Vocoder Streaming" opcodes. All of these opcodes begin with the characters "pvs". These opcodes became part of Csound through the work of Richard Dobson, Victor Lazzarini and others. They are designed to work in realtime in the frequency domain in Csound and indeed they are not just very fast but also easier to use than FFT implementations in many other applications.
Changing from Time-domain to Frequency-domain
For dealing with signals in the frequency domain, the pvs opcodes implement a new signal type, the f-signals. Csound shows the type of a variable in the first letter of its name. Each audio signal starts with an a, each control signal with a k, and so each signal in the frequency domain used by the pvs-opcodes starts with an f.
There are several ways to create an f-signal. The most common way is to convert an audio signal to a frequency signal. The first example covers two typical situations:
- the audio signal derives from playing back a soundfile from the hard disc (instr 1)
- the audio signal is the live input (instr 2)
(Caution - this example can quickly start feeding back. Best results are with headphones.)
EXAMPLE 05I01_pvsanal.csd 1
<CsoundSynthesizer>
<CsOptions>
-i adc -o dac
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
;uses the file "fox.wav" (distributed with the Csound Manual)
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
;general values for fourier transform
gifftsiz = 1024
gioverlap = 256
giwintyp = 1 ;von hann window
instr 1 ;soundfile to fsig
asig soundin "fox.wav"
fsig pvsanal asig, gifftsiz, gioverlap, gifftsiz*2, giwintyp
aback pvsynth fsig
outs aback, aback
endin
instr 2 ;live input to fsig
prints "LIVE INPUT NOW!%n"
ain inch 1 ;live input from channel 1
fsig pvsanal ain, gifftsiz, gioverlap, gifftsiz, giwintyp
alisten pvsynth fsig
outs alisten, alisten
endin
</CsInstruments>
<CsScore>
i 1 0 3
i 2 3 10
</CsScore>
</CsoundSynthesizer>
You should hear first the "fox.wav" sample, and then the slightly delayed live input signal. The delay (or latency) that you will observe will depend first of all on the general settings for realtime input (ksmps, -b and -B: see chapter 2D), but it will also be added to by the FFT process. The window size here is 1024 samples, so the additional delay is 1024/44100 = 0.023 seconds. If you change the window size gifftsiz to 2048 or to 512 samples, you should notice a larger or shorter delay. For realtime applications, the decision about the FFT size is not only a question of better time resolution versus better frequency resolution, but it will also be a question concerning tolerable latency.
What happens in the example above? Firstly, the audio signal (asig, ain) is being analyzed and transformed to an f-signal. This is done via the opcode pvsanal. Then nothing more happens than the f-signal being transformed from the frequency domain signal back into the time domain (an audio signal). This is called inverse Fourier transformation (IFT or IFFT) and is carried out by the opcode pvsynth.2 In this case, it is just a test: to see if everything works, to hear the results of different window sizes and to check the latency, but potentially you can insert any other pvs opcode(s) in between this analysis and resynthesis:

Pitch shifting
Simple pitch shifting can be carried out by the opcode pvscale. All the frequency data in the f-signal are scaled by a certain value. Multiplying by 2 results in transposing by an octave upwards; multiplying by 0.5 in transposing by an octave downwards. For accepting cent values instead of ratios as input, the cent opcode can be used.
EXAMPLE 05I02_pvscale.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;example by joachim heintz
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
gifftsize = 1024
gioverlap = gifftsize / 4
giwinsize = gifftsize
giwinshape = 1; von-Hann window
instr 1 ;scaling by a factor
ain soundin "fox.wav"
fftin pvsanal ain, gifftsize, gioverlap, giwinsize, giwinshape
fftscal pvscale fftin, p4
aout pvsynth fftscal
out aout
endin
instr 2 ;scaling by a cent value
ain soundin "fox.wav"
fftin pvsanal ain, gifftsize, gioverlap, giwinsize, giwinshape
fftscal pvscale fftin, cent(p4)
aout pvsynth fftscal
out aout/3
endin
</CsInstruments>
<CsScore>
i 1 0 3 1; original pitch
i 1 3 3 .5; octave lower
i 1 6 3 2 ;octave higher
i 2 9 3 0
i 2 9 3 400 ;major third
i 2 9 3 700 ;fifth
e
</CsScore>
</CsoundSynthesizer>
Pitch shifting via FFT resynthesis is very simple in general, but rather more complicated in detail. With speech for instance, there is a problem because of the formants. If you simply scale the frequencies, the formants are shifted, too, and the sound gets the typical 'helium voice' effect. There are some parameters in the pvscale opcode, and some other pvs-opcodes which can help to avoid this, but the quality of the results will always depend to an extend upon the nature of the input sound.
Time-stretch/compress
As the Fourier transformation separates the spectral information from its progression in time, both elements can be varied independently. Pitch shifting via the pvscale opcode, as in the previous example, is independent of the speed of reading the audio data. The complement is changing the time without changing the pitch: time-stretching or time-compression.
The simplest way to alter the speed of a sampled sound is using pvstanal (new in Csound 5.13). This opcode transforms a sound stored in a function table (transformation to an f-signal is carried out internally by the opcode) with time manipulations simply being done by altering its ktimescal parameter.
EXAMPLE 05I03_pvstanal.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;example by joachim heintz
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
;store the sample "fox.wav" in a function table (buffer)
gifil ftgen 0, 0, 0, 1, "fox.wav", 0, 0, 1
;general values for the pvstanal opcode
giamp = 1 ;amplitude scaling
gipitch = 1 ;pitch scaling
gidet = 0 ;onset detection
giwrap = 0 ;no loop reading
giskip = 0 ;start at the beginning
gifftsiz = 1024 ;fft size
giovlp = gifftsiz/8 ;overlap size
githresh = 0 ;threshold
instr 1 ;simple time stretching / compressing
fsig pvstanal p4, giamp, gipitch, gifil, gidet, giwrap, giskip,
gifftsiz, giovlp, githresh
aout pvsynth fsig
out aout
endin
instr 2 ;automatic scratching
kspeed randi 2, 2, 2 ;speed randomly between -2 and 2
kpitch randi p4, 2, 2 ;pitch between 2 octaves lower or higher
fsig pvstanal kspeed, 1, octave(kpitch), gifil
aout pvsynth fsig
aenv linen aout, .003, p3, .1
out aenv
endin
</CsInstruments>
<CsScore>
; speed
i 1 0 3 1
i . + 10 .33
i . + 2 3
s
i 2 0 10 0;random scratching without ...
i . 11 10 2 ;... and with pitch changes
</CsScore>
</CsoundSynthesizer>
Cross Synthesis
Working in the frequency domain makes it possible to combine or 'cross' the spectra of two sounds. As the Fourier transform of an analysis frame results in a frequency and an amplitude value for each frequency 'bin', there are many different ways of performing cross synthesis. The most common methods are:
- Combine the amplitudes of sound A with the frequencies of sound B. This is the classical phase vocoder approach. If the frequencies are not completely from sound B, but represent an interpolation between A and B, the cross synthesis is more flexible and adjustable. This is what pvsvoc does.
- Combine the frequencies of sound A with the amplitudes of sound B. Give user flexibility by scaling the amplitudes between A and B: pvscross.
- Get the frequencies from sound A. Multiply the amplitudes of A and B. This can be described as spectral filtering. pvsfilter gives a flexible portion of this filtering effect.
This is an example of phase vocoding. It is nice to have speech as sound A, and a rich sound, like classical music, as sound B. Here the "fox" sample is being played at half speed and 'sings' through the music of sound B:
EXAMPLE 05I04_phase_vocoder.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;example by joachim heintz
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
;store the samples in function tables (buffers)
gifilA ftgen 0, 0, 0, 1, "fox.wav", 0, 0, 1
gifilB ftgen 0, 0, 0, 1, "ClassGuit.wav", 0, 0, 1
;general values for the pvstanal opcode
giamp = 1 ;amplitude scaling
gipitch = 1 ;pitch scaling
gidet = 0 ;onset detection
giwrap = 1 ;loop reading
giskip = 0 ;start at the beginning
gifftsiz = 1024 ;fft size
giovlp = gifftsiz/8 ;overlap size
githresh = 0 ;threshold
instr 1
;read "fox.wav" in half speed and cross with classical guitar sample
fsigA pvstanal .5, giamp, gipitch, gifilA, gidet, giwrap, giskip,\
gifftsiz, giovlp, githresh
fsigB pvstanal 1, giamp, gipitch, gifilB, gidet, giwrap, giskip,\
gifftsiz, giovlp, githresh
fvoc pvsvoc fsigA, fsigB, 1, 1
aout pvsynth fvoc
aenv linen aout, .1, p3, .5
out aenv
endin
</CsInstruments>
<CsScore>
i 1 0 11
</CsScore>
</CsoundSynthesizer>
The next example introduces pvscross:
EXAMPLE 05I05_pvscross.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;example by joachim heintz
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
;store the samples in function tables (buffers)
gifilA ftgen 0, 0, 0, 1, "BratscheMono.wav", 0, 0, 1
gifilB ftgen 0, 0, 0, 1, "fox.wav", 0, 0, 1
;general values for the pvstanal opcode
giamp = 1 ;amplitude scaling
gipitch = 1 ;pitch scaling
gidet = 0 ;onset detection
giwrap = 1 ;loop reading
giskip = 0 ;start at the beginning
gifftsiz = 1024 ;fft size
giovlp = gifftsiz/8 ;overlap size
githresh = 0 ;threshold
instr 1
;cross viola with "fox.wav" in half speed
fsigA pvstanal 1, giamp, gipitch, gifilA, gidet, giwrap, giskip,\
gifftsiz, giovlp, githresh
fsigB pvstanal .5, giamp, gipitch, gifilB, gidet, giwrap, giskip,\
gifftsiz, giovlp, githresh
fcross pvscross fsigA, fsigB, 0, 1
aout pvsynth fcross
aenv linen aout, .1, p3, .5
out aenv
endin
</CsInstruments>
<CsScore>
i 1 0 11
</CsScore>
</CsoundSynthesizer>
The last example shows spectral filtering via pvsfilter. The well-known "fox" (sound A) is now filtered by the viola (sound B). Its resulting intensity is dependent upon the amplitudes of sound B, and if the amplitudes are strong enough, you will hear a resonating effect:
EXAMPLE 05I06_pvsfilter.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
;example by joachim heintz
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
;store the samples in function tables (buffers)
gifilA ftgen 0, 0, 0, 1, "fox.wav", 0, 0, 1
gifilB ftgen 0, 0, 0, 1, "BratscheMono.wav", 0, 0, 1
;general values for the pvstanal opcode
giamp = 1 ;amplitude scaling
gipitch = 1 ;pitch scaling
gidet = 0 ;onset detection
giwrap = 1 ;loop reading
giskip = 0 ;start at the beginning
gifftsiz = 1024 ;fft size
giovlp = gifftsiz/4 ;overlap size
githresh = 0 ;threshold
instr 1
;filters "fox.wav" (half speed) by the spectrum of the viola (double speed)
fsigA pvstanal .5, giamp, gipitch, gifilA, gidet, giwrap, giskip,\
gifftsiz, giovlp, githresh
fsigB pvstanal 2, 5, gipitch, gifilB, gidet, giwrap, giskip,\
gifftsiz, giovlp, githresh
ffilt pvsfilter fsigA, fsigB, 1
aout pvsynth ffilt
aenv linen aout, .1, p3, .5
out aenv
endin
</CsInstruments>
<CsScore>
i 1 0 11
</CsScore>
</CsoundSynthesizer>
There are many more tools and opcodes for transforming FFT signals in Csound. Have a look at the Signal Processing II section of the Opcodes Overview for some hints.
- All soundfiles used in this manual are free and can be downloaded at www.csound-tutorial.net^
- In some cases it might be interesting to use pvsadsyn instead of pvsynth. It employs a bank of oscillators for resynthesis, the details of which can be controlled by the user.^
K. ANALYSIS TRANSFORMATION SYNTHESIS
1. The ATS technique.
General overview.
The ATS technique (Analysis-Transformation-Synthesis) was developed by Juan Pampin. A comprehensive explanation of this technique can be found in his ATS Theory1 but, essentially, it may be said that it represents two aspects of the analyzed signal: the deterministic part and the stochastic or residual part. This model was initially conceived by Julius Orion Smith and Xavier Serra,2 but ATS refines certain aspects of it, such as the weighting of the spectral components on the basis of their Signal-to-Mask-Ratio (SMR).3
The deterministic part consists in sinusoidal trajectories with varying amplitude, frequency and phase. It is achieved by means of the depuration of the spectral data obtained using STFT (Short-Time Fourier Transform) analysis.
The stochastic part is also termed residual, because it is achieved by subtracting the deterministic signal from the original signal. For such purposes, the deterministic part is synthesized preserving the phase alignment of its components in the second step of the analysis. The residual part is represented with noise variable energy values along the 25 critical bands.4
The ATS technique has the following advantages:
- The splitting between deterministic and stochastic parts allows an independent treatment of two different qualitative aspects of an audio signal.
- The representation of the deterministic part by means of sinusoidal trajectories improves the information and presents it on a way that is much closer to the way that musicians think of sound. Therefore, it allows many 'classical' spectral transformations (such as the suppression of partials or their frequency warping) in a more flexible and conceptually clearer way.
- The representation of the residual part by means of noise values among the 25 critical bands simplifies the information and its further reconstruction. Namely, it is possible to overcome the common artifacts that arise in synthesis using oscillator banks or IDFT, when the time of a noisy signal analyzed using a FFT is warped.
The ATS file format
Instead of storing the 'crude' data of the FFT analysis, the ATS files store a representation of a digital sound signal in terms of sinusoidal trajectories (called partials) with instantaneous frequency, amplitude, and phase changing along temporal frames. Each frame has a set of partials, each having (at least) amplitude and frequency values (phase information might be discarded from the analysis). Each frame might also contain noise information, modeled as time-varying energy in the 25 critical bands of the analysis residual. All the data is stored as 64 bits floats in the host's byte order.
The ATS files start with a header at which their description is stored (such as frame rate, duration, number of sinusoidal trajectories, etc.). The header of the ATS files contains the following information:
- ats-magic-number (just the arbitrary number 123. for consistency checking)
- sampling-rate (samples/sec)
- frame-size (samples)
- window-size (samples)
- partials (number of partials)
- frames (number of frames)
- ampmax (max. amplitude)
- frqmax (max. frequency)
- dur (duration in sec.)
- type (frame type, see below)
The ATS frame type may be, at present, one of the four following:
Type 1: only sinusoidal trajectories with amplitude and frequency data.
Type 2: only sinusoidal trajectories with amplitude, frequency and phase data.
Type 3: sinusoidal trajectories with amplitude, and frequency data as well as residual data.
Type 4: sinusoidal trajectories with amplitude, frequency and phase data as well as residual data.
So, after the header, an ATS file with frame type 4, np number of partials and nf frames will have:
Frame 1: Amp.of partial 1, Freq. of partial 1, Phase of partial 1 ....................................................................................... ....................................................................................... Amp.of partial np, Freq. of partial np, Phase of partial np Residual energy value for critical band 1 .................................................................. .................................................................. Residual energy value for critical band 25 ........................................................................................................ Frame nf: Amp.of partial 1, Freq. of partial 1, Phase of partial 1 ....................................................................................... ....................................................................................... Amp.of partial np, Freq. of partial np, Phase of partial np Residual energy value for critical band 1 .................................................................. .................................................................. Residual energy value for critical band 25
As an example, an ATS file of frame type 4, with 100 frames and 10 partials will need:
A header with 10 double floats values.
100*10*3 double floats for storing the Amplitude, Frequency and Phase values of 10 partials along 100 frames.
25*100 double floats for storing the noise information of the 25 critical bands along 100 frames.
Header: 10*8 = 80 bytes Deterministic data: 3000*8 = 24000 bytes Residual data: 2500*8 = 20000 bytes Total: 80 + 24000 + 20000 = 44080 bytes
The following Csound code shows how to retrieve the data of the header of an ATS file.
EXAMPLE 05K01_ats_header.csd
<CsoundSynthesizer> <CsOptions> -n -m0 </CsOptions> <CsInstruments> sr = 44100 ksmps = 32 nchnls = 1 0dbfs = 1 ;Some macros #define ATS_SR # 0 # ;sample rate (Hz) #define ATS_FS # 1 # ;frame size (samples) #define ATS_WS # 2 # ;window Size (samples) #define ATS_NP # 3 # ;number of Partials #define ATS_NF # 4 # ;number of Frames #define ATS_AM # 5 # ;maximum Amplitude #define ATS_FM # 6 # ;maximum Frequency (Hz) #define ATS_DU # 7 # ;duration (seconds) #define ATS_TY # 8 # ;ATS file Type instr 1 iats_file=p4 ;instr1 just reads the file header and loads its data into several variables ;and prints the result in the Csound prompt. i_sampling_rate ATSinfo iats_file, $ATS_SR i_frame_size ATSinfo iats_file, $ATS_FS i_window_size ATSinfo iats_file, $ATS_WS i_number_of_partials ATSinfo iats_file, $ATS_NP i_number_of_frames ATSinfo iats_file, $ATS_NF i_max_amp ATSinfo iats_file, $ATS_AM i_max_freq ATSinfo iats_file, $ATS_FM i_duration ATSinfo iats_file, $ATS_DU i_ats_file_type ATSinfo iats_file, $ATS_TY print i_sampling_rate print i_frame_size print i_window_size print i_number_of_partials print i_number_of_frames print i_max_amp print i_max_freq print i_duration print i_ats_file_type endin </CsInstruments> <CsScore> ;change to put any ATS file you like #define ats_file #"../ats-files/basoon-C4.ats"# ; st dur atsfile i1 0 0 $ats_file e </CsScore> </CsoundSynthesizer> ;Example by Oscar Pablo Di Liscia
2. Performing ATS analysis with the ATSA command-line utility of Csound.
All the Csound Opcodes devoted to ATS Synthesis need to read an ATS Analysis file. ATS was initially developed for the CLM environment (Common Lisp Music), but at present there exist several GNU applications that can perform ATS analysis, among them the Csound Package command-line utility ATSA which is based on the ATSA program (Di Liscia, Pampin, Moss) and was ported to Csound by Istvan Varga. The ATSA program (Di Liscia, Pampin, Moss) may be obtained at:
https://github.com/jamezilla/ats/tree/master/ats
Graphical Resources for displaying ATS analysis files.
If a plot of the ATS files is required, the ATSH software (Di Liscia, Pampin, Moss) may be used. ATSH is a C program that uses the GTK graphic environment. The source code and compilation directives can be obtained at:
https://github.com/jamezilla/ats/tree/master/ats
Another very good GUI program that can be used for such purposes is Qatsh, a Qt 4 port by Jean-Philippe Meuret. This one can be obtained at:
http://sourceforge.net/apps/trac/speed-dreams/browser/subprojects/soundeditor/trunk?rev=5250
Parameters explanation. How to get a good analysis. What a good analysis is.
The analysis parameters are somewhat numerous, and must be carefully tuned in order to obtain good results. A detailed explanation of the meaning of these parameters can be found at:
http://musica.unq.edu.ar/personales/odiliscia/software/ATSH-doc.htm
In order to get a good analysis, the sound to be analysed should meet the following requirements:
- The ATS analysis was meant to analyse isolated, individual sounds. This means that the analysis of sequences and/or superpositions of sounds, though possible, is not likely to render optimal results.
- Must have been recorded with a good signal-to-noise ratio, and should not contain unwanted noises.
- Must have been recorded without reverberation and/or echoes.
A good ATS analysis should meet the following requirements:
- Must have a good temporal resolution of the frequency, amplitude, phase and noise (if any) data. The tradeoff between temporal and frequency resolution is a very well known issue in FFT based spectral analysis.
- The Deterministic and Stochastic (also termed "residual") data must be reasonably separated in their respective ways of representation. This means that, if a sound has both, deterministic and stochastic data, the former must be represented by sinusoidal trajectories, whilst the latter must be represented by energy values among the 25 critical bands. This allows a more effective treatment of both types of data in the synthesis and transformation processes.
- If the analysed sound is pitched, the sinusoidal trajectories (Deterministic) should be as stable as possible and ordered according the original sound harmonics. This means that the trajectory #1 should represent the first (fundamental) harmonic, the trajectory #2 should represent the second harmonic, and so on. This allow to perform easily further transformation processes during resynthesis (such as, for example, selecting the odd harmonics to give them a different treatment than the others).
Whilst the first requirement is unavoidable, in order to get a useful analysis, the second and third ones are sometimes almost impossible to meet in full and their accomplishment depends often on the user objectives.
3. Synthesizing ATS analysis files.
Synthesis techniques applied to ATS.
The synthesis techniques that are usually applied in order to get a synthesized sound that resembles the original sound as much as possible are detailed explained in Pampin 20115 and di Liscia 20136 . However, it is worth pointing out that once the proper data is stored in an analysis file, the user is free to read and apply to this data any reasonable transformation/synthesis technique/s, thereby facilitating the creation of new and interesting sounds that need not be similar nor resemble the original sound.
Csound Opcodes for Reading ATS files data:
ATSread, ATSreadnz, ATSbufread, ATSinterpread, ATSpartialtap.
The former Csound opcodes were essentially developed to read ATS data from ATS files and were written by Alex Norman.
ATSread
This opcode reads the deterministic ATS data from an ATS file. It outputs frequency/amplitude pairs of a sinusoidal trajectory corresponding to a specific partial number, according to a time pointer that must be delivered. As the unit works at k-rate, the frequency and amplitude data must be interpolated in order to avoid unwanted clicks in the resynthesis.
The following example reads and synthesizes the 10 partials of an ATS analysis corresponding to a steady 440 cps flute sound. Since the instrument is designed to synthesize only one partial of the ATS file, the mixing of several of them must be obtained performing several notes in the score (the use of Csound's macros is strongly recommended in this case). Though not the most practical way of synthesizing ATS data, this method facilitates individual control of the frequency and amplitude values of each one of the partials, which is not possible any other way. In the example that follows, even numbered partials are attenuated in amplitude, resulting in a sound that resembles a clarinet. Amplitude and frequency envelopes could also be used in order to affect a time changing weighting of the partials. Finally, the amplitude and frequency values could be used to drive other synthesis units, such as filters or FM synthesis networks of oscillators.
EXAMPLE 05K02_atsread.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
instr 1
iamp = p4 ;amplitude scaler
ifreq = p5 ;frequency scaler
ipar = p6 ;partial required
itab = p7 ;audio table
iatsfile = p8 ;ats file
idur ATSinfo iatsfile, 7 ;get duration
ktime line 0, p3, idur ;time pointer
kfreq, kamp ATSread ktime, iatsfile, ipar ;get frequency and amplitude values
aamp interp kamp ;interpolate amplitude values
afreq interp kfreq ;interpolate frequency values
aout oscil3 aamp*iamp, afreq*ifreq, itab ;synthesize with amp and freq scaling
out aout
endin
</CsInstruments>
<CsScore>
; sine wave table
f 1 0 16384 10 1
#define atsfile #"../ats-files/flute-A5.ats"#
; start dur amp freq par tab atsfile
i1 0 3 1 1 1 1 $atsfile
i1 0 . .1 . 2 . $atsfile
i1 0 . 1 . 3 . $atsfile
i1 0 . .1 . 4 . $atsfile
i1 0 . 1 . 5 . $atsfile
i1 0 . .1 . 6 . $atsfile
i1 0 . 1 . 7 . $atsfile
i1 0 . .1 . 8 . $atsfile
i1 0 . 1 . 9 . $atsfile
i1 0 . .1 . 10 . $atsfile
e
</CsScore>
</CsoundSynthesizer>
;example by Oscar Pablo Di Liscia
In Csound6, you can use arrays to simplify the code, and to choose different numbers of partials:
EXAMPLE 05K03_atsread2.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
gS_ATS_file = "../ats-files/flute-A5.ats" ;ats file
giSine ftgen 0, 0, 16384, 10, 1 ; sine wave table
instr Master ;call instr "Play" for each partial
iNumParts = p4 ;how many partials to synthesize
idur ATSinfo gS_ATS_file, 7 ;get ats file duration
iAmps[] array 1, .1 ;array for even and odd partials
iParts[] genarray 1,iNumParts ;creates array [1, 2, ..., iNumParts]
indx = 0 ;initialize index
;loop for number of elements in iParts array
until indx == iNumParts do
;call an instance of instr "Play" for each partial
event_i "i", "Play", 0, p3, iAmps[indx%2], iParts[indx], idur
indx += 1 ;increment index
od ;end of do ... od block
turnoff ;turn this instrument off as job has been done
endin
instr Play
iamp = p4 ;amplitude scaler
ipar = p5 ;partial required
idur = p6 ;ats file duration
ktime line 0, p3, idur ;time pointer
kfreq, kamp ATSread ktime, gS_ATS_file, ipar ;get frequency and amplitude values
aamp interp kamp ;interpolate amplitude values
afreq interp kfreq ;interpolate frequency values
aout oscil3 aamp*iamp, afreq, giSine ;synthesize with amp scaling
out aout
endin
</CsInstruments>
<CsScore>
; strt dur number of partials
i "Master" 0 3 1
i . + . 3
i . + . 10
</CsScore>
</CsoundSynthesizer>
;example by Oscar Pablo Di Liscia and Joachim Heintz
ATSreadnz
This opcode is similar to ATSread in the sense that it reads the noise data of an ATS file, delivering k-rate energy values for the requested critical band. In order to this Opcode to work, the input ATS file must be either type 3 or 4 (types 1 and 2 do not contain noise data). ATSreadnz is simpler than ATSread, because whilst the number of partials of an ATS file is variable, the noise data (if any) is stored always as 25 values per analysis frame each value corresponding to the energy of the noise in each one of the critical bands. The three required arguments are: a time pointer, an ATS file name and the number of critical band required (which, of course, must have a value between 1 and 25).
The following example is similar to the previous. The instrument is designed to synthesize only one noise band of the ATS file, the mixing of several of them must be obtained performing several notes in the score. In this example the synthesis of the noise band is done using Gaussian noise filtered with a resonator (i.e., band-pass) filter. This is not the method used by the ATS synthesis Opcodes that will be further shown, but its use in this example is meant to lay stress again on the fact that the use of the ATS analysis data may be completely independent of its generation. In this case, also, a macro that performs the synthesis of the 25 critical bands was programmed. The ATS file used correspond to a female speech sound that lasts for 3.633 seconds, and in the examples is stretched to 10.899 seconds, that is three times its original duration. This shows one of the advantages of the Deterministic plus Stochastic data representation of ATS: the stochastic ("noisy") part of a signal may be stretched in the resynthesis without the artifacts that arise commonly when the same data is represented by cosine components (as in the FFT based resynthesis). Note that, because the Stochastic noise values correspond to energy (i.e., intensity), in order to get the proper amplitude values, the square root of them must be computed.
EXAMPLE 05K04_atsreadnz.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
instr 1
itabc = p7 ;table with the 25 critical band frequency edges
iscal = 1 ;reson filter scaling factor
iamp = p4 ;amplitude scaler
iband = p5 ;energy band required
if1 table iband-1, itabc ;lower edge
if2 table iband, itabc ;upper edge
idif = if2-if1
icf = if1 + idif*.5 ;center frequency value
ibw = icf*p6 ;bandwidth
iatsfile = p8 ;ats file name
idur ATSinfo iatsfile, 7 ;get duration
ktime line 0, p3, idur ;time pointer
ken ATSreadnz ktime, iatsfile, iband ;get frequency and amplitude values
anoise gauss 1
aout reson anoise*sqrt(ken), icf, ibw, iscal ;synthesize with amp and freq scaling
out aout*iamp
endin
</CsInstruments>
<CsScore>
; sine wave table
f1 0 16384 10 1
;the 25 critical bands edge's frequencies
f2 0 32 -2 0 100 200 300 400 510 630 770 920 1080 1270 1480 1720 2000 2320 \
2700 3150 3700 4400 5300 6400 7700 9500 12000 15500 20000
;an ats file name
#define atsfile #"../ats-files/female-speech.ats"#
;a macro that synthesize the noise data along all the 25 critical bands
#define all_bands(start'dur'amp'bw'file)
#
i1 $start $dur $amp 1 $bw 2 $file
i1 . . . 2 . . $file
i1 . . . 3 . . .
i1 . . . 4 . . .
i1 . . . 5 . . .
i1 . . . 6 . . .
i1 . . . 7 . . .
i1 . . . 8 . . .
i1 . . . 9 . . .
i1 . . . 10 . . .
i1 . . . 11 . . .
i1 . . . 12 . . .
i1 . . . 13 . . .
i1 . . . 14 . . .
i1 . . . 15 . . .
i1 . . . 16 . . .
i1 . . . 17 . . .
i1 . . . 18 . . .
i1 . . . 19 . . .
i1 . . . 20 . . .
i1 . . . 21 . . .
i1 . . . 22 . . .
i1 . . . 23 . . .
i1 . . . 24 . . .
i1 . . . 25 . . .
#
;ditto...original sound duration is 3.633 secs.
;stretched 300%
$all_bands(0'10.899'1'.05'$atsfile)
e
</CsScore>
</CsoundSynthesizer>
;example by Oscar Pablo Di Liscia
ATSbufread, ATSinterpread, ATSpartialtap.
The ATSbufread opcode reads an ATS file and stores its frequency and amplitude data into an internal table. The first and third input arguments are the same as in the ATSread and the ATSreadnz Opcodes: a time pointer and an ATS file name. The second input argument is a frequency scaler. The fourth argument is the number of partials to be stored. Finally, this Opcode may take two optional arguments: the first partial and the increment of partials to be read, which default to 0 and 1 respectively.
Although this opcode does not have any output, the ATS frequency and amplitude data is available to be used by other opcode. In this case, two examples are provided, the first one uses the ATSinterpread opcode and the second one uses the ATSpartialtap opcode.
The ATSinterpread opcode reads an ATS table generated by the ATSbufread opcode and outputs amplitude values interpolating them between the two amplitude values of the two frequency trajectories that are closer to a given frequency value. The only argument that this opcode takes is the desired frequency value.
The following example synthesizes five sounds. All the data is taken from the ATS file "test.ats". The first and final sounds match the two frequencies closer to the first and the second partials of the analysis file and have their amplitude values closer to the ones in the original ATS file. The other three sounds (second, third and fourth), have frequencies that are in-between the ones of the first and second partials of the ATS file, and their amplitudes are scaled by an interpolation between the amplitudes of the first and second partials. The more the frequency requested approaches the one of a partial, the more the amplitude envelope rendered by ATSinterpread is similar to the one of this partial. So, the example shows a gradual "morphing" beween the amplitude envelope of the first partial to the amplitude envelope of the second according to their frequency values.
EXAMPLE 05K05_atsinterpread.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
instr 1
iamp = p4 ;amplitude scaler
ifreq = p5 ;frequency scaler
iatsfile = p7 ;atsfile
itab = p6 ;audio table
ifreqscal = 1 ;frequency scaler
ipars ATSinfo iatsfile, 3 ;how many partials
idur ATSinfo iatsfile, 7 ;get duration
ktime line 0, p3, idur ;time pointer
ATSbufread ktime, ifreqscal, iatsfile, ipars ;reads an ATS buffer
kamp ATSinterpread ifreq ;get the amp values according to freq
aamp interp kamp ;interpolate amp values
aout oscil3 aamp, ifreq, itab ;synthesize
out aout*iamp
endin
</CsInstruments>
<CsScore>
; sine wave table
f 1 0 16384 10 1
#define atsfile #"../ats-files/test.ats"#
; start dur amp freq atab atsfile
i1 0 3 1 440 1 $atsfile ;first partial
i1 + 3 1 550 1 $atsfile ;closer to first partial
i1 + 3 1 660 1 $atsfile ;half way between both
i1 + 3 1 770 1 $atsfile ;closer to second partial
i1 + 3 1 880 1 $atsfile ;second partial
e
</CsScore>
</CsoundSynthesizer>
;example by Oscar Pablo Di Liscia
The ATSpartialtap Opcode reads an ATS table generated by the ATSbufread Opcode and outputs the frequency and amplitude k-rate values of a specific partial number. The example presented here uses four of these opcodes that read from a single ATS buffer obtained using ATSbufread in order to drive the frequency and amplitude of four oscillators. This allows the mixing of different combinations of partials, as shown by the three notes triggered by the designed instrument.
EXAMPLE 05K06_atspartialtap.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
instr 1
iamp = p4/4 ;amplitude scaler
ifreq = p5 ;frequency scaler
itab = p6 ;audio table
ip1 = p7 ;first partial to be synthesized
ip2 = p8 ;second partial to be synthesized
ip3 = p9 ;third partial to be synthesized
ip4 = p10 ;fourth partial to be synthesized
iatsfile = p11 ;atsfile
ipars ATSinfo iatsfile, 3 ;get how many partials
idur ATSinfo iatsfile, 7 ;get duration
ktime line 0, p3, idur ;time pointer
ATSbufread ktime, ifreq, iatsfile, ipars ;reads an ATS buffer
kf1,ka1 ATSpartialtap ip1 ;get the amp values according each partial number
af1 interp kf1
aa1 interp ka1
kf2,ka2 ATSpartialtap ip2 ;ditto
af2 interp kf2
aa2 interp ka2
kf3,ka3 ATSpartialtap ip3 ;ditto
af3 interp kf3
aa3 interp ka3
kf4,ka4 ATSpartialtap ip4 ;ditto
af4 interp kf4
aa4 interp ka4
a1 oscil3 aa1, af1*ifreq, itab ;synthesize each partial
a2 oscil3 aa2, af2*ifreq, itab ;ditto
a3 oscil3 aa3, af3*ifreq, itab ;ditto
a4 oscil3 aa4, af4*ifreq, itab ;ditto
out (a1+a2+a3+a4)*iamp
endin
</CsInstruments>
<CsScore>
; sine wave table
f 1 0 16384 10 1
#define atsfile #"../ats-files/oboe-A5.ats"#
; start dur amp freq atab part#1 part#2 part#3 part#4 atsfile
i1 0 3 10 1 1 1 5 11 13 $atsfile
i1 + 3 7 1 1 1 6 14 17 $atsfile
i1 + 3 400 1 1 15 16 17 18 $atsfile
e
</CsScore>
</CsoundSynthesizer>
;example by Oscar Pablo Di Liscia
Synthesizing ATS data: ATSadd, ATSaddnz, ATSsinnoi. ATScross.
The four opcodes that will be presented in this section synthesize ATS analysis data internally and allow for some modifications of these data as well. A significant difference to the preceding opcodes is that the synthesis method cannot be chosen by the user. The synthesis methods used by all of these opcodes are fully explained in:
[1] Juan Pampin, 2011. ATS_theory
http://wiki.dxarts.washington.edu/groups/general/wiki/39f07/attachments/55bd6/ATS_theory.pdf
[2] Oscar Pablo Di Liscia, 2013. A Pure Data toolkit for real-time synthesis of ATS spectral data
http://lac.linuxaudio.org/2013/papers/26.pdf
The ATSadd opcode synthesizes deterministic data from an ATS file using an array of table lookup oscillators whose amplitude and frequency values are obtained by linear interpolation of the ones in the ATS file according to the time of the analysis requested by a time pointer (see [2] for more details). The frequency of all the partials may be modified at k-rate, allowing shifting and/or frequency modulation. An ATS file, a time pointer and a function table are required. The table is supposed to contain either a cosine or a sine function, but nothing prevents the user from experimenting with other functions. Some care must be taken in the last case, so as not to produce foldover (frequency aliasing). The user may also request a number of partials smaller than the number of partials of the ATS file (by means of the inpars variable in the example below). There are also two optional arguments: a partial offset (i.e., the first partial that will be taken into account for the synthesis, by means of the ipofst variable in the example below) and a step to select the partials (by means of the inpincr variable in the example below). Default values for these arguments are 0 and 1 respectively. Finally, the user may define a final optional argument that references a function table that will be used to rescale the amplitude values during the resynthesis. The amplitude values of all the partials along all the frames are rescaled to the table length and used as indexes to lookup a scaling amplitude value in the table. For example, in a table of size 1024, the scaling amplitude of all the 0.5 amplitude values (-6 dBFS) that are found in the ATS file is in the position 512 (1024*0.5). Very complex filtering effects can be obtained by carefully setting these gating tables according to the amplitude values of a particular ATS analysis.
EXAMPLE 05K07_atsadd.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
;Some macros
#define ATS_NP # 3 # ;number of Partials
#define ATS_DU # 7 # ;duration
instr 1
/*read some ATS data from the file header*/
iatsfile = p11
i_number_of_partials ATSinfo iatsfile, $ATS_NP
i_duration ATSinfo iatsfile, $ATS_DU
iamp = p4 ;amplitude scaler
ifreqdev = 2^(p5/12) ;frequency deviation (p5=semitones up or down)
itable = p6 ;audio table
/*here we deal with number of partials, offset and increment issues*/
inpars = (p7 < 1 ? i_number_of_partials : p7) ;inpars can not be <=0
ipofst = (p8 < 0 ? 0 : p8) ;partial offset can not be < 0
ipincr = (p9 < 1 ? 1 : p9) ;partial increment can not be <= 0
imax = ipofst + inpars*ipincr ;max. partials allowed
if imax <= i_number_of_partials igoto OK
;if we are here, something is wrong!
;set npars to zero, so as the output will be zero and the user knows
print imax, i_number_of_partials
inpars = 0
ipofst = 0
ipincr = 1
OK: ;data is OK
/********************************************************************/
igatefn = p10 ;amplitude scaling table
ktime linseg 0, p3, i_duration
asig ATSadd ktime, ifreqdev, iatsfile, itable, inpars, ipofst, ipincr, igatefn
out asig*iamp
endin
</CsInstruments>
<CsScore>
;change to put any ATS file you like
#define ats_file #"../ats-files/basoon-C4.ats"#
;audio table (sine)
f1 0 16384 10 1
;some tables to test amplitude gating
;f2 reduce progressively partials with amplitudes from 0.5 to 1 (-6dBFs to 0 dBFs)
;and eliminate partials with amplitudes below 0.5 (-6dBFs)
f2 0 1024 7 0 512 0 512 1
;f3 boost partials with amplitudes from 0 to 0.125 (-12dBFs)
;and attenuate partials with amplitudes from 0.125 to 1 (-12dBFs to 0dBFs)
f3 0 1024 -5 8 128 8 896 .001
; start dur amp freq atable npars offset pincr gatefn atsfile
i1 0 2.82 1 0 1 0 0 1 0 $ats_file
i1 + . 1 0 1 0 0 1 2 $ats_file
i1 + . .8 0 1 0 0 1 3 $ats_file
e
</CsScore>
</CsoundSynthesizer>
;example by Oscar Pablo Di Liscia
The ATSaddnz opcode synthesizes residual ("noise") data from an ATS file using the method explained in [1] and [2]. This opcode works in a similar fashion to ATSadd except that frequency warping of the noise bands is not permitted and the maximum number of noise bands will always be 25 (the 25 critical bands, see Zwiker/Fastl, footnote 3). The optional arguments offset and increment work in a similar fashion to that in ATSadd. The ATSaddnz opcode allows the synthesis of several combinations of noise bands, but individual amplitude scaling of them is not possible.
EXAMPLE 05K08_atsaddnz.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
;Some macros
#define NB # 25 # ;number noise bands
#define ATS_DU # 7 # ;duration
instr 1
/*read some ATS data from the file header*/
iatsfile = p8
i_duration ATSinfo iatsfile, $ATS_DU
iamp = p4 ;amplitude scaler
/*here we deal with number of partials, offset and increment issues*/
inb = (p5 < 1 ? $NB : p5) ;inb can not be <=0
ibofst = (p6 < 0 ? 0 : p6) ;band offset cannot be < 0
ibincr = (p7 < 1 ? 1 : p7) ;band increment cannot be <= 0
imax = ibofst + inb*ibincr ;max. bands allowed
if imax <= $NB igoto OK
;if we are here, something is wrong!
;set nb to zero, so as the output will be zero and the user knows
print imax, $NB
inb = 0
ibofst = 0
ibincr = 1
OK: ;data is OK
/********************************************************************/
ktime linseg 0, p3, i_duration
asig ATSaddnz ktime, iatsfile, inb, ibofst, ibincr
out asig*iamp
endin
</CsInstruments>
<CsScore>
;change to put any ATS file you like
#define ats_file #"../ats-files/female-speech.ats"#
; start dur amp nbands bands_offset bands_incr atsfile
i1 0 7.32 1 25 0 1 $ats_file ;all bands
i1 + . . 15 10 1 $ats_file ;from 10 to 25 step 1
i1 + . . 8 1 3 $ats_file ;from 1 to 24 step 3
i1 + . . 5 15 1 $ats_file ;from 15 to 20 step 1
e
</CsScore>
</CsoundSynthesizer>
;example by Oscar Pablo Di Liscia
The ATSsinnoi opcode synthesizes both deterministic and residual ("noise") data from an ATS file using the method explained in [1] and [2]. This opcode may be regarded as a combination of the two previous opcodes but with the allowance of individual amplitude scaling of the mixes of deterministic and residual parts. All the arguments of ATSsinnoi are the same as those for the two previous opcodes, except for the two k-rate variables ksinlev and knoislev that allow individual, and possibly time-changing, scaling of the deterministic and residual parts of the synthesis.
EXAMPLE 05K09_atssinnoi.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
;Some macros
#define ATS_NP # 3 # ;number of Partials
#define ATS_DU # 7 # ;duration
instr 1
iatsfile = p11
/*read some ATS data from the file header*/
i_number_of_partials ATSinfo iatsfile, $ATS_NP
i_duration ATSinfo iatsfile, $ATS_DU
print i_number_of_partials
iamp = p4 ;amplitude scaler
ifreqdev = 2^(p5/12) ;frequency deviation (p5=semitones up or down)
isinlev = p6 ;deterministic part gain
inoislev = p7 ;residual part gain
/*here we deal with number of partials, offset and increment issues*/
inpars = (p8 < 1 ? i_number_of_partials : p8) ;inpars can not be <=0
ipofst = (p9 < 0 ? 0 : p9) ;partial offset can not be < 0
ipincr = (p10 < 1 ? 1 : p10) ;partial increment can not be <= 0
imax = ipofst + inpars*ipincr ;max. partials allowed
if imax <= i_number_of_partials igoto OK
;if we are here, something is wrong!
;set npars to zero, so as the output will be zero and the user knows
prints "wrong number of partials requested", imax, i_number_of_partials
inpars = 0
ipofst = 0
ipincr = 1
OK: ;data is OK
/********************************************************************/
ktime linseg 0, p3, i_duration
asig ATSsinnoi ktime, isinlev, inoislev, ifreqdev, iatsfile, inpars, ipofst, ipincr
out asig*iamp
endin
</CsInstruments>
<CsScore>
;change to put any ATS file you like
#define ats_file #"../ats-files/female-speech.ats"#
; start dur amp freqdev sinlev noislev npars offset pincr atsfile
i1 0 3.66 .79 0 1 0 0 0 1 $ats_file
;deterministic only
i1 + 3.66 .79 0 0 1 0 0 1 $ats_file
;residual only
i1 + 3.66 .79 0 1 1 0 0 1 $ats_file
;deterministic and residual
; start dur amp freqdev sinlev noislev npars offset pincr atsfile
i1 + 3.66 2.5 0 1 0 80 60 1 $ats_file
;from partial 60 to partial 140, deterministic only
i1 + 3.66 2.5 0 0 1 80 60 1 $ats_file
;from partial 60 to partial 140, residual only
i1 + 3.66 2.5 0 1 1 80 60 1 $ats_file
;from partial 60 to partial 140, deterministic and residual
e
</CsScore>
</CsoundSynthesizer>
;example by Oscar Pablo Di Liscia
ATScross is an opcode that performs some kind of "interpolation" of the amplitude data between two ATS analyses. One of these two ATS analyses must be obtained using the ATSbufread opcode (see above) and the other is to be loaded by an ATScross instance. Only the deterministic data of both analyses is used. The ATS file, time pointer, frequency scaling, number of partials, partial offset and partial increment arguments work the same way as usages in previously described opcodes. Using the arguments kmylev and kbuflev the user may define how much of the amplitude values of the file read by ATSbufread is to be used to scale the amplitude values corresponding to the frequency values of the analysis read by ATScross. So, a value of 0 for kbuflev and 1 for kmylev will retain the original ATS analysis read by ATScross unchanged whilst the converse (kbuflev =1 and kmylev=0) will retain the frequency values of the ATScross analysis but scaled by the amplitude values of the ATSbufread analysis. As the time pointers of both units need not be the same, and frequency warping and number of partials may also be changed, very complex cross synthesis and sound hybridation can be obtained using this opcode.
EXAMPLE 05K10_atscross.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
;ATS files
#define ats1 #"../ats-files/flute-A5.ats"#
#define ats2 #"../ats-files/oboe-A5.ats"#
instr 1
iamp = p4 ;general amplitude scaler
ilev1 = p5 ;level of iats1 partials
ifd1 = 2^(p6/12) ;frequency deviation for iats1 partials
ilev2 = p7 ;level of ats2 partials
ifd2 = 2^(p8/12) ;frequency deviation for iats2 partials
itau = p9 ;audio table
/*get ats file data*/
inp1 ATSinfo $ats1, 3
inp2 ATSinfo $ats2, 3
idur1 ATSinfo $ats1, 7
idur2 ATSinfo $ats2, 7
ktime line 0, p3, idur1
ktime2 line 0, p3, idur2
ATSbufread ktime, ifd1, $ats1, inp1
aout ATScross ktime2, ifd2, $ats2, itau, ilev2, ilev1, inp2
out aout*iamp
endin
</CsInstruments>
<CsScore>
; sine wave for the audio table
f1 0 16384 10 1
; start dur amp lev1 f1 lev2 f2 table
i1 0 2.3 .75 0 0 1 0 1 ;original oboe
i1 + . . 0.25 . .75 . . ;oboe 75%, flute 25%
i1 + . . 0.5 . 0.5 . . ;oboe 50%, flute 50%
i1 + . . .75 . .25 . . ;oboe 25%, flute 75%
i1 + . . 1 . 0 . . ;oboe partials with flute's amplitudes
e
</CsScore>
</CsoundSynthesizer>
;example by Oscar Pablo Di Liscia
- Juan Pampin. 2011. ATS_theory, http://wiki.dxarts.washington.edu/groups/general/wiki/39f07/attachments/55bd6/ATS_theory.pdf^
- Xavier Serra and Julius O. Smith III. 1990. A Sound Analysis/Synthesis System Based on a Deterministic plus Stochastic Decomposition, Computer Music Journal, Vol.14 #4, MIT Press, USA.^
- Ernst Zwiker and Hugo Fastl. 1990. Psychoacoustics Facts and Models. Springer, Berlin, Heidelberg.^
- Cf. Zwiker/Fastl (above footnote).^
- Juan Pampin. 2011. ATS_theory, http://wiki.dxarts.washington.edu/groups/general/wiki/39f07/attachments/55bd6/ATS_theory.pdf^
- Oscar Pablo Di Liscia, 2013. A Pure Data toolkit for real-time synthesis of ATS spectral data http://lac.linuxaudio.org/2013/papers/26.pdf^
AMPLITUDE AND PITCH TRACKING
Tracking the amplitude of an audio signal is a relatively simple procedure but simply following the amplitude values of the waveform is unlikely to be useful. An audio waveform will be bipolar, expressing both positive and negative values, so to start with, some sort of rectifying of the negative part of the signal will be required. The most common method of achieving this is to square it (raise to the power of 2) and then to take the square root. Squaring any negative values will provide positive results (-2 squared equals 4). Taking the square root will restore the absolute values.
An audio signal is an oscillating signal, periodically passing through amplitude zero but these zero amplitudes do not necessarily imply that the signal has decayed to silence as our brain perceives it. Some sort of averaging will be required so that a tracked amplitude of close to zero will only be output when the signal has settled close to zero for some time. Sampling a set of values and outputting their mean will produce a more acceptable sequence of values over time for a signal's change in amplitude. Sample group size will be important: too small a sample group may result in some residual ripple in the output signal, particularly in signals with only low frequency content, whereas too large a group may result in a sluggish response to sudden changes in amplitude. Some judgement and compromise is required.
The procedure described above is implemented in the following example. A simple audio note is created that ramps up and down according to a linseg envelope. In order to track its amplitude, audio values are converted to k-rate values and are then squared, then square rooted and then written into sequential locations of an array 31 values long. The mean is calculated by summing all values in the array and divided by the length of the array. This procedure is repeated every k-cycle. The length of the array will be critical in fine tuning the response for the reasons described in the preceding paragraph. Control rate (kr) will also be a factor therefore is taken into consideration when calculating the size of the array. Changing control rate (kr) or number of audio samples in a control period (ksmps) will then no longer alter response behaviour.
EXAMPLE 05L01_Amplitude_Tracking_First_Principles.csd
<CsoundSynthesizer>
<CsOptions>
-dm0 -odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 16
nchnls = 1
0dbfs = 1
; a rich waveform
giwave ftgen 1,0, 512, 10, 1,1/2,1/3,1/4,1/5
instr 1
; create an audio signal
aenv linseg 0,p3/2,1,p3/2,0 ; triangle shaped envelope
aSig poscil aenv,300,giwave ; audio oscillator
out aSig ; send audio to output
; track amplitude
kArr[] init 500 / ksmps ; initialise an array
kNdx init 0 ; initialise index for writing to array
kSig downsamp aSig ; create k-rate version of audio signal
kSq = kSig ^ 2 ; square it (negatives become positive)
kRoot = kSq ^ 0.5 ; square root it (restore absolute values)
kArr[kNdx] = kRoot ; write result to array
kMean = sumarray(kArr) / lenarray(kArr) ; calculate mean of array
printk 0.1,kMean ; print mean to console
; increment index and wrap-around if end of the array is met
kNdx wrap kNdx+1, 0, lenarray(kArr)
endin
</CsInstruments>
<CsScore>
i 1 0 5
</CsScore>
</CsoundSynthesizer>
In practice it is not necessary for us to build our own amplitude tracker as Csound already offers several opcodes for the task. rms outputs a k-rate amplitude tracking signal by employing mathematics similar to those described above. follow outputs at a-rate and uses a sample and hold method as it outputs data, probably necessitating some sort of low-pass filtering of the output signal. follow2 also outputs at a-rate but smooths the output signal by different amounts depending on whether the amplitude is rising or falling.
A quick comparison of these three opcodes and the original method from first principles is given below:
The sound file used in all three comparisons is 'fox.wav' which can be found as part of the Csound HTML Manual download. This sound is someone saying: “the quick brown fox jumps over the lazy dog”.
First of all by employing the the technique exemplified in example 05L01, the amplitude following signal is overlaid upon the source signal:
It can be observed that the amplitude tracking signal follows the amplitudes of the input signal reasonably well. A slight delay in response at sound onsets can be observed as the array of values used by the averaging mechanism fills with appropriately high values. As discussed earlier, reducing the size of the array will improve response at the risk of introducing ripple. Another approach to dealing with the issue of ripple is to low-pass filter the signal output by the amplitude follower. This is an approach employed by the follow2 opcode. The second thing that is apparent is that the amplitude following signal does not attain the peak value of the input signal. At its peaks, the amplitude following signal is roughly 1/3 of the absolute peak value of the input signal. How close it gets to the absolute peak amplitude depends somewhat on the dynamic nature of the input signal. If an input signal sustains a peak amplitude for some time then the amplitude following signal will tend to this peak value.
The rms opcode employs a method similar to that used in the previous example but with the convenience of an encapsulated opcode. Its output superimposed upon the waveform is shown below:
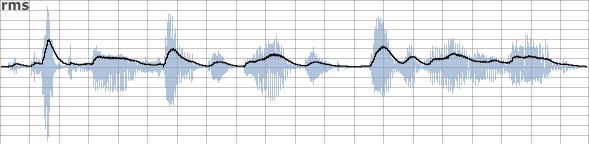
Its method of averaging uses filtering rather than simply taking a mean of a buffer of amplitude values. rms allows us to set the cutoff frequency (kCf) of its internal filter:
kRms rms aSig, kCf
This is an optional argument which defaults to 10. Lowering this value will dampen changes in rms and smooth out ripple, raising it will improve the response but increase the audibility of ripple. A choice can be made based on some foreknowledge of the input audio signal: dynamic percussive input audio might demand faster response whereas audio that dynamically evolves gradually might demand greater smoothing.
The follow opcode uses a sample-and-hold mechanism when outputting the tracked amplitude. This can result in a stepped output that might require addition lowpass filtering before use. We actually defined the period, the duration for which values are held, using its second input argument. The update rate will be one over the period. In the following example the audio is amplitude tracked using the following line:
aRms follow aSig, 0.01
with the following result:
The hump over the word spoken during the third and fourth time divisions initially seem erroneous but it is a result of greater amplitude excursion into the negative domain. follow provides a better reflection of absolute peak amplitude.
follow2 uses a different algorithm with smoothing on both upward and downward slopes of the tracked amplitude. We can define different values for attack and decay time. In the following example the decay time is much longer than the attack time. The relevant line of code is:
iAtt = 0.04 iRel = 0.5 aTrk follow2 aSig, 0.04, 0.5
and the result of amplitude tracking is:
This technique can be used to extend the duration of short input sound events or triggers. Note that the attack and release times for follow2 can also be modulated at k-rate.
Dynamic Gating and Amplitude Triggering
Once we have traced the changing amplitude of an audio signal it is straightforward to use specific changes in that function to trigger other events within Csound. The simplest technique would be to simply define a threshold above which one thing happens and below which something else happens. A crude dynamic gating of the signal above could be implemented thus:
EXAMPLE 05L02_Simple_Dynamic_Gate.csd
<CsoundSynthesizer> <CsOptions> -dm0 -odac </CsOptions> <CsInstruments> ksmps = 32 0dbfs = 1 ; this is a necessary definition, ; otherwise amplitude will be -32768 to 32767 instr 1 aSig diskin "fox.wav", 1 ; read sound file kRms rms aSig ; scan rms iThreshold = 0.1 ; rms threshold kGate = kRms > iThreshold ? 1 : 0 ; gate either 1 or zero aGate interp kGate ; interpolate to create smoother on->off->on switching aSig = aSig * aGate ; multiply signal by gate out aSig ; send to output endin </CsInstruments> <CsScore> i 1 0 10 </CsScore> </CsoundSynthesizer>
Once a dynamic threshold has been defined, in this case 0.1, the RMS value is interrogated every k-cycle as to whether it is above or below this value. If it is above, then the variable kGate adopts a value of '1' (open) or if below, kGate is zero (closed). This on/off switch could just be multiplied to the audio signal to turn it on or off according to the status of the gate but clicks would manifest each time the gates opens or closes so some sort of smoothing or ramping of the gate signal is required. In this example I have simply interpolated it using the 'interp' opcode to create an a-rate signal which is then multiplied to the original audio signal. This means that a linear ramp with be added across the duration of a k-cycle in audio samples – in this case 32 samples. A more elaborate approach might involve portamento and low-pass filtering.
The results of this dynamic gate are shown below:

The threshold is depicted as a red line. It can be seen that each time the RMS value (the black line) drops below the threshold the audio signal (blue waveform) is muted.
The simple solution described above can prove adequate in applications where the user wishes to sense sound event onsets and convert them to triggers but in more complex situations, in particular when a new sound event occurs whilst the previous event is still sounding and pushing the RMS above the threshold, this mechanism will fail. In these cases triggering needs to depend upon dynamic change rather than absolute RMS values. If we consider a two-event sound file where two notes sound on a piano, the second note sounding while the first is still decaying, triggers generated using the RMS threshold mechanism from the previous example will only sense the first note onset. (In the diagram below this sole trigger is illustrated by the vertical black line.) Raising the threshold might seem to be remedial action but is not ideal as this will prevent quietly played notes from generating triggers.
It will often be more successful to use magnitudes of amplitude increase to decide whether to generate a trigger or not. The two critical values in implementing such a mechanism are the time across which a change will be judged ('iSampTim' in the example) and the amount of amplitude increase that will be required to generate a trigger (iThresh). An additional mechanism to prevent double triggerings if an amplitude continues to increase beyond the time span of a single sample period will also be necessary. What this mechanism will do is to bypass the amplitude change interrogation code for a user-definable time period immediately after a trigger has been generated (iWait). A timer which counts elapsed audio samples (kTimer) is used to time how long to wait before retesting amplitude changes.
If we pass our piano sound file through this instrument, the results look like this:

This time we correctly receive two triggers, one at the onset of each note.
The example below tracks audio from the sound-card input channel 1 using this mechanism.
EXAMPLE 05L03_Dynamic_Trigger.csd
<CsoundSynthesizer> <CsOptions> -dm0 -iadc -odac </CsOptions> <CsInstruments> sr = 44100 ksmps = 32 nchnls = 2 0dbfs = 1 instr 1 iThresh = 0.1 ; change threshold aSig inch 1 ; live audio in iWait = 1000 ; prevent repeats wait time (in samples) kTimer init 1001 ; initial timer value kRms rms aSig, 20 ; track amplitude iSampTim = 0.01 ; time across which change in RMS will be measured kRmsPrev delayk kRms, iSampTim ; delayed RMS (previous) kChange = kRms - kRmsPrev ; change if(kTimer>iWait) then ; if we are beyond the wait time... kTrig = kChange > iThresh ? 1 : 0 ; trigger if threshold exceeded kTimer = kTrig == 1 ? 0 : kTimer ; reset timer when a trigger generated else ; otherwise (we are within the wait time buffer) kTimer += ksmps ; increment timer kTrig = 0 ; cancel trigger endif schedkwhen kTrig,0,0,2,0,0.1 ; trigger a note event endin instr 2 aEnv transeg 0.2, p3, -4, 0 ; decay envelope aSig poscil aEnv, 400 ; 'ping' sound indicator out aSig ; send audio to output endin </CsInstruments> <CsScore> i 1 0 [3600*24*7] </CsScore> </CsoundSynthesizer>
Pitch Tracking
Csound currently provides five opcode options for pitch tracking. In ascending order of newness they are: pitch, pitchamdf, pvspitch, ptrack and plltrack. Related to these opcodes are pvscent and centroid but rather than track the harmonic fundamental, they track the spectral centroid of a signal. An example and suggested application for centroid is given a little later on in this chapter.
Each offers a slightly different set of features – some offer simultaneous tracking of both amplitude and pitch, some only pitch tracking. None of these opcodes provide more than one output for tracked frequency therefore none offer polyphonic tracking although in a polyphonic tone the fundamental of the strongest tone will most likely be tracked. Pitch tracking presents many more challenges than amplitude tracking therefore a degree of error can be expected and will be an issue that demands addressing. To get the best from any pitch tracker it is important to consider preparation of the input signal – either through gating or filtering – and also processing of the output tracking data, for example smoothing changes through the use of filtering opcode such as port, median filtering to remove erratic and erroneous data and a filter to simply ignore obviously incorrect data. Parameters for these procedures will rely upon some prior knowledge of the input signal, the pitch range of an instrument for instance. A particularly noisy environment or a distant microphone placement might demand more aggressive noise gating. In general some low-pass filtering of the input signal will always help in providing a more stable frequency tracking signal. Something worth considering is that the attack portion of a note played on an acoustic instrument generally contains a lot of noisy, harmonically chaotic material. This will tend to result in slightly chaotic movement in the pitch tracking signal, we may therefore wish to sense the onset of a note and only begin tracking pitch once the sustain portion has begun. This may be around 0.05 seconds after the note has begun but will vary from instrument to instrument and from note to note. In general lower notes will have a longer attack. However we do not really want to overestimate the duration of this attack stage as this will result in a sluggish pitch tracker. Another specialised situation is the tracking of pitch in singing – we may want to gate sibilant elements ('sss', 't' etc.). pvscent can be useful in detecting the difference between vowels and sibilants.
'pitch' is the oldest of the pitch tracking opcodes on offer and provides the widest range of input parameters.
koct, kamp pitch asig, iupdte, ilo, ihi, idbthresh [, ifrqs] [, iconf] \
[, istrt] [, iocts] [, iq] [, inptls] [, irolloff] [, iskip]
This makes it somewhat more awkward to use initially (although many of its input parameters are optional) but some of its options facilitate quite specialised effects. Firstly it outputs its tracking signal in 'oct' format. This might prove to be a useful format but conversion to other formats is easy anyway. Apart from a number of parameters intended to fine tune the production of an accurate signal it allows us to specify the number of octave divisions used in quantising the output. For example if we give this a value of 12 we have created the basis of a simple chromatic 'autotune' device. We can also quantise the procedure in the time domain using its 'update period' input. Material with quickly changing pitch or vibrato will require a shorter update period (which will demand more from the CPU). It has an input control for 'threshold of detection' which can be used to filter out and disregard pitch and amplitude tracking data beneath this limit. Pitch is capable of very good pitch and amplitude tracking results in real-time.
pitchamdf uses the so-called 'Average Magnitude Difference Function' method. It is perhaps slightly more accurate than pitch as a general purpose pitch tracker but its CPU demand is higher.
pvspitch uses streaming FFT technology to track pitch. It takes an f-signal as input which will have to be created using the pvsanal opcode. At this step the choice of FFT size will have a bearing upon the performance of the pvspitch pitch tracker. Smaller FFT sizes will allow for faster tracking but with perhaps some inaccuracies, particularly with lower pitches whereas larger FFT sizes are likely to provide for more accurate pitch tracking at the expense of some time resolution. pvspitch tries to mimic certain functions of the human ear in how it tries to discern pitch. pvspitch works well in real-time but it does have a tendency to jump its output to the wrong octave – an octave too high – particularly when encountering vibrato.
ptrack also makes uses of streaming FFT but takes an normal audio signal as input, performing the FFT analysis internally. We still have to provide a value for FFT size with the same considerations mentioned above. ptrack is based on an algorithm by Miller Puckette, the co-creator of MaxMSP and creator of PD. ptrack also works well in real-time but it does have a tendency to jump to erroneous pitch tracking values when pitch is changing quickly or when encountering vibrato. Median filtering (using the mediank opcode) and filtering of outlying values might improve the results.
plltrack uses a phase-locked loop algorithm in detecting pitch. plltrack is another efficient real-time option for pitch tracking. It has a tendency to gliss up and down from very low frequency values at the start and end of notes, i.e. when encountering silence. This effect can be minimised by increasing its 'feedback' parameter but this can also make pitch tracking unstable over sustained notes.
In conclusion, pitch is probably still the best choice as a general purpose pitch tracker, pitchamdf is also a good choice. pvspitch, ptrack and plltrack all work well in real-time but might demand additional processing to remove errors.
pvscent and centroid are a little different to the other pitch trackers in that, rather than try to discern the fundemental of a harmonic tone, they assess what the centre of gravity of a spectrum is. An application for this is in the identification of different instruments playing the same note. Softer, darker instruments, such as the french horn, will be characterised by a lower centroid to that of more shrill instruments, such as the violin.
Both opcodes use FFT. Centroid works directly with an audio signal input whereas pvscent requires an f-sig input. Centroid also features a trigger input which allows us to manually trigger it to update its output. In the following example we use centroid to detect individual drums sounds – bass drum, snare drum, cymbal – within a drum loop. We will use the dynamic amplitude trigger from earlier on in this chapter to detect when sound onsets are occurring and use this trigger to activate centroid and also then to trigger another instrument with a replacement sound. Each percussion instrument in the original drum loop will be replaced with a different sound: bass drums will be replaced with a kalimba/thumb piano sound, snare drums will be replaced by hand claps (a la TR-808), and cymbal sounds will be replaced with tambourine sounds. The drum loop used is beats.wav which can be found with the download of the Csound HTML manual (and within the Csound download itself). This loop is not ideal as some of the instruments coincide with one another – for example, the first consists of a bass drum and a snare drum played together. The 'beat replacer' will inevitably make a decision one way or the other but is not advanced enough to detect both instruments playing simultaneously. The critical stage is the series of if... elseifs... at the bottom of instrument 1 where decisions are made about instruments' identities according to what centroid band they fall into. The user can fine tune the boundary division values to modify the decision making process. centroid values are also printed to the terminal when onsets are detected which might assist in this fine tuning.
EXAMPLE 05L04_Drum_Replacement.csd
<CsoundSynthesizer>
<CsOptions>
-dm0 -odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
instr 1
asig diskin "beats.wav",1
iThreshold = 0.05
iWait = 0.1*sr
kTimer init iWait+1
iSampTim = 0.02 ; time across which RMS change is measured
kRms rms asig ,20
kRmsPrev delayk kRms,iSampTim ; rms from earlier
kChange = kRms - kRmsPrev ; change (+ve or -ve)
if kTimer > iWait then ; prevent double triggerings
; generate a trigger
kTrigger = kChange > iThreshold ? 1 : 0
; if trigger is generated, reset timer
kTimer = kTrigger == 1 ? 0 : kTimer
else
kTimer += ksmps ; increment timer
kTrigger = 0 ; clear trigger
endif
ifftsize = 1024
; centroid triggered 0.02 after sound onset to avoid noisy attack
kDelTrig delayk kTrigger,0.02
kcent centroid asig, kDelTrig, ifftsize ; scan centroid
printk2 kcent ; print centroid values
if kDelTrig==1 then
if kcent>0 && kcent<2500 then ; first freq. band
event "i","Cowbell",0,0.1
elseif kcent<8000 then ; second freq. band
event "i","Clap",0,0.1
else ; third freq. band
event "i","Tambourine",0,0.5
endif
endif
endin
instr Cowbell
kenv1 transeg 1,p3*0.3,-30,0.2, p3*0.7,-30,0.2
kenv2 expon 1,p3,0.0005
kenv = kenv1*kenv2
ipw = 0.5
a1 vco2 0.65,562,2,0.5
a2 vco2 0.65,845,2,0.5
amix = a1+a2
iLPF2 = 10000
kcf expseg 12000,0.07,iLPF2,1,iLPF2
alpf butlp amix,kcf
abpf reson amix, 845, 25
amix dcblock2 (abpf*0.06*kenv1)+(alpf*0.5)+(amix*0.9)
amix buthp amix,700
amix = amix*0.5*kenv
out amix
endin
instr Clap
if frac(p1)==0 then
event_i "i", p1+0.1, 0, 0.02
event_i "i", p1+0.1, 0.01, 0.02
event_i "i", p1+0.1, 0.02, 0.02
event_i "i", p1+0.1, 0.03, 2
else
kenv transeg 1,p3,-25,0
iamp random 0.7,1
anoise dust2 kenv*iamp, 8000
iBPF = 1100
ibw = 2000
iHPF = 1000
iLPF = 1
kcf expseg 8000,0.07,1700,1,800,2,500,1,500
asig butlp anoise,kcf*iLPF
asig buthp asig,iHPF
ares reson asig,iBPF,ibw,1
asig dcblock2 (asig*0.5)+ares
out asig
endif
endin
instr Tambourine
asig tambourine 0.3,0.01 ,32, 0.47, 0, 2300 , 5600, 8000
out asig ;SEND AUDIO TO OUTPUTS
endin
</CsInstruments>
<CsScore>
i 1 0 10
</CsScore>
</CsoundSynthesizer>
06 SAMPLES
RECORD AND PLAY SOUNDFILES
Playing Soundfiles From Disk - diskin21
The simplest way of playing a sound file from Csound is to use the diskin2 opcode. This opcode reads audio directly from the hard drive location where it is stored, i.e. it does not pre-load the sound file at initialisation time. This method of sound file playback is therefore good for playing back very long, or parts of very long, sound files. It is perhaps less well suited to playing back sound files where dense polyphony, multiple iterations and rapid random access to the file is required. In these situations reading from a function table or buffer is preferable.
diskin2 has additional parameters for speed of playback, and interpolation.
EXAMPLE 06A01_Play_soundfile.csd
<CsoundSynthesizer>
<CsOptions>
-odac ; activate real-time audio output
</CsOptions>
<CsInstruments>
; example written by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
instr 1 ; play audio from disk
kSpeed init 1 ; playback speed
iSkip init 0 ; inskip into file (in seconds)
iLoop init 0 ; looping switch (0=off 1=on)
; read audio from disk using diskin2 opcode
a1 diskin2 "loop.wav", kSpeed, iSkip, iLoop
out a1 ; send audio to outputs
endin
</CsInstruments>
<CsScore>
i 1 0 6
e
</CsScore>
</CsoundSynthesizer>
Writing Audio to Disk
The traditional method of rendering Csound's audio to disk is to specify a sound file as the audio destination in the Csound command or under <CsOptions>. In fact before real-time performance became a possibility this was the only way in which Csound was used. With this method, all audio that is piped to the output using out, outs etc. will be written to this file. The number of channels that the file will contain will be determined by the number of channels specified in the orchestra header using 'nchnls'. The disadvantage of this method is that we cannot simultaneously listen to the audio in real-time.
EXAMPLE 06A02_Write_soundfile.csd
<CsoundSynthesizer>
<CsOptions>
; audio output destination is given as a sound file (wav format specified)
; this method is for deferred time performance,
; simultaneous real-time audio will not be possible
-oWriteToDisk1.wav -W
</CsOptions>
<CsInstruments>
; example written by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giSine ftgen 0, 0, 4096, 10, 1 ; a sine wave
instr 1 ; a simple tone generator
aEnv expon 0.2, p3, 0.001 ; a percussive envelope
aSig poscil aEnv, cpsmidinn(p4), giSine ; audio oscillator
out aSig ; send audio to output
endin
</CsInstruments>
<CsScore>
; two chords
i 1 0 5 60
i 1 0.1 5 65
i 1 0.2 5 67
i 1 0.3 5 71
i 1 3 5 65
i 1 3.1 5 67
i 1 3.2 5 73
i 1 3.3 5 78
e
</CsScore>
</CsoundSynthesizer>
Writing Audio to Disk with Simultaneous Real-time Audio Output - fout and monitor
Recording audio output to disk whilst simultaneously monitoring in real-time is best achieved through combining the opcodes monitor and fout. 'monitor' can be used to create an audio signal that consists of a mix of all audio output from all instruments. This audio signal can then be rendered to a sound file on disk using 'fout'. 'monitor' can read multi-channel outputs but its number of outputs should correspond to the number of channels defined in the header using 'nchnls'. In this example it is read just in mono. 'fout' can write audio in a number of formats and bit depths and it can also write multi-channel sound files.
EXAMPLE 06A03_Write_RT.csd
<CsoundSynthesizer>
<CsOptions>
-odac ; activate real-time audio output
</CsOptions>
<CsInstruments>
;example written by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giSine ftgen 0, 0, 4096, 10, 1 ; a sine wave
gaSig init 0; set initial value for global audio variable (silence)
instr 1 ; a simple tone generator
aEnv expon 0.2, p3, 0.001 ; percussive amplitude envelope
aSig poscil aEnv, cpsmidinn(p4), giSine ; audio oscillator
out aSig
endin
instr 2 ; write to a file (always on in order to record everything)
aSig monitor ; read audio from output bus
fout "WriteToDisk2.wav",4,aSig ; write audio to file (16bit mono)
endin
</CsInstruments>
<CsScore>
; activate recording instrument to encapsulate the entire performance
i 2 0 8.3
; two chords
i 1 0 5 60
i 1 0.1 5 65
i 1 0.2 5 67
i 1 0.3 5 71
i 1 3 5 65
i 1 3.1 5 67
i 1 3.2 5 73
i 1 3.3 5 78
e
</CsScore>
</CsoundSynthesizer
- diskin2 is an improved version of diskin. In Csound 6, both will use the same code, so it should make no difference whether you use diskin or diskin2.^
RECORD AND PLAY BUFFERS
Playing Audio From RAM - flooper2
Csound offers many opcodes for playing back sound files that have first been loaded into a function table (and therefore are loaded into RAM). Some of these offer higher quality at the expense of computation speed; some are simpler and less fully featured.
One of the newer and easier to use opcodes for this task is flooper2. As its name might suggest it is intended for the playback of files with looping. 'flooper2' can also apply a cross-fade between the end and the beginning of the loop in order to smooth the transition where looping takes place.
In the following example a sound file that has been loaded into a GEN01 function table is played back using 'flooper2'. 'flooper2' also includes a parameter for modulating playback speed/pitch. There is also the option of modulating the loop points at k-rate. In this example the entire file is simply played and looped. You can replace the sound file with one of your own or you can download the one used in the example from here.
Some notes about GEN01 and function table sizes:
When storing sound files in GEN01 function tables we must ensure that we define a table of sufficient size to store our sound file. Normally function table sizes should be powers of 2 (2, 4, 8, 16, 32 etc.). If we know the duration of our sound file, we can derive the required table size by multiplying this duration by the sample rate and then choosing the next power of 2 larger than this. For example when the sampling rate is 44100, we will require 44100 table locations to store 1 second of audio; but 44100 is not a power of 2 so we must choose the next power of 2 larger than this which is 65536. (Hint: you can discover a sound file's duration by using Csound's 'sndinfo' utility.)
There are some 'lazy' options however: if we underestimate the table size when we then run Csound, it will warn us that this table size is too small and conveniently inform us via the terminal what the minimum size required to store the entire file would be - we can then substitute this value in our GEN01 table. We can also overestimate the table size in which case Csound won't complain at all, but this is a rather inefficient approach.
If we give table size a value of zero we have what is referred to as 'deferred table size'. This means that Csound will calculate the exact table size needed to store our sound file and use this as the table size but this will probably not be a power of 2. Many of Csound's opcodes will work quite happily with non-power of 2 function table sizes, but not all! It is a good idea to know how to deal with power of 2 table sizes. We can also explicitly define non-power of 2 table sizes by prefacing the table size with a minus sign '-'.
All of the above discussion about required table sizes assumed that the sound file was mono; to store a stereo sound file will naturally require twice the storage space, for example, 1 second of stereo audio will require 88200 storage locations. GEN01 will indeed store stereo sound files and many of Csound's opcodes will read from stereo GEN01 function tables, but again not all! We must be prepared to split stereo sound files, either to two sound files on disk or into two function tables using GEN01's 'channel' parameter (p8), depending on the opcodes we are using.
Storing audio in GEN01 tables as mono channels with non-deferred and power of 2 table sizes will ensure maximum compatibility.
EXAMPLE 06B01_flooper2.csd
<CsoundSynthesizer>
<CsOptions>
-odac ; activate real-time audio
</CsOptions>
<CsInstruments>
; example written by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
; STORE AUDIO IN RAM USING GEN01 FUNCTION TABLE
giSoundFile ftgen 0, 0, 262144, 1, "loop.wav", 0, 0, 0
instr 1 ; play audio from function table using flooper2 opcode
kAmp = 1 ; amplitude
kPitch = p4 ; pitch/speed
kLoopStart = 0 ; point where looping begins (in seconds)
kLoopEnd = nsamp(giSoundFile)/sr; loop end (end of file)
kCrossFade = 0 ; cross-fade time
; read audio from the function table using the flooper2 opcode
aSig flooper2 kAmp,kPitch,kLoopStart,kLoopEnd,kCrossFade,giSoundFile
out aSig ; send audio to output
endin
</CsInstruments>
<CsScore>
; p4 = pitch
; (sound file duration is 4.224)
i 1 0 [4.224*2] 1
i 1 + [4.224*2] 0.5
i 1 + [4.224*1] 2
e
</CsScore>
</CsoundSynthesizer>
Csound's Built-in Record-Play Buffer - sndloop
Csound has an opcode called sndloop which provides a simple method of recording some audio into a buffer and then playing it back immediately. The duration of audio storage required is defined when the opcode is initialized. In the following example two seconds is provided. Once activated, as soon as two seconds of live audio has been recorded by 'sndloop', it immediately begins playing it back in a loop. 'sndloop' allows us to modulate the speed/pitch of the played back audio as well as providing the option of defining a crossfade time between the end and the beginning of the loop. In the example pressing 'r' on the computer keyboard activates record followed by looped playback, pressing 's' stops record or playback, pressing '+' increases the speed and therefore the pitch of playback and pressing '-' decreases the speed/pitch of playback. If playback speed is reduced below zero it enters the negative domain, in which case playback will be reversed.
You will need to have a microphone connected to your computer in order to use this example.
EXAMPLE 06B02_sndloop.csd
<CsoundSynthesizer>
<CsOptions>
; real-time audio in and out are both activated
-iadc -odac
</CsOptions>
<CsInstruments>
;example written by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
instr 1
; PRINT INSTRUCTIONS
prints "Press 'r' to record, 's' to stop playback, "
prints "'+' to increase pitch, '-' to decrease pitch.\\n"
; SENSE KEYBOARD ACTIVITY
kKey sensekey; sense activity on the computer keyboard
aIn inch 1 ; read audio from first input channel
kPitch init 1 ; initialize pitch parameter
iDur init 2 ; inititialize duration of loop parameter
iFade init 0.05 ; initialize crossfade time parameter
if kKey = 114 then ; if 'r' has been pressed...
kTrig = 1 ; set trigger to begin record-playback
elseif kKey = 115 then ; if 's' has been pressed...
kTrig = 0 ; set trigger to turn off record-playback
elseif kKey = 43 then ; if '+' has been pressed...
kPitch = kPitch + 0.02 ; increment pitch parameter
elseif kKey = 45 then ; if '-' has been pressed
kPitch = kPitch - 0.02 ; decrement pitch parameter
endif ; end of conditional branches
; CREATE SNDLOOP INSTANCE
aOut, kRec sndloop aIn, kPitch, kTrig, iDur, iFade ; (kRec output is not used)
out aOut ; send audio to output
endin
</CsInstruments>
<CsScore>
i 1 0 3600 ; instr 1 plays for 1 hour
</CsScore>
</CsoundSynthesizer>
Recording to and Playback from a Function Table
Writing to and reading from buffers can also be achieved through the use of Csound's opcodes for table reading and writing operations. Although the procedure is a little more complicated than that required for 'sndloop' it is ultimately more flexible. In the next example separate instruments are used for recording to the table and for playing back from the table. Another instrument which runs constantly scans for activity on the computer keyboard and activates the record or playback instruments accordingly. For writing to the table we will use the tablew opcode and for reading from the table we will use the table opcode (if we were to modulate the playback speed it would be better to use one of Csound's interpolating variations of 'table' such as tablei or table3. Csound writes individual values to table locations, the exact table locations being defined by an 'index'. For writing continuous audio to a table this index will need to be continuously moving 1 location for every sample. This moving index (or 'pointer') can be created with an a-rate line or a phasor. The next example uses 'line'. When using Csound's table operation opcodes we first need to create that table, either in the orchestra header or in the score. The duration of the audio buffer can be calculated from the size of the table. In this example the table is 2^17 points long, that is 131072 points. The duration in seconds is this number divided by the sample rate which in our example is 44100Hz. Therefore maximum storage duration for this example is 131072/44100 which is around 2.9 seconds.
EXAMPLE 06B03_RecPlayToTable.csd
<CsoundSynthesizer>
<CsOptions>
; real-time audio in and out are both activated
-iadc -odac -d -m0
</CsOptions>
<CsInstruments>
; example written by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
giBuffer ftgen 0, 0, 2^17, 7, 0; table for audio data storage
maxalloc 2,1 ; allow only one instance of the recording instrument at a time!
instr 1 ; Sense keyboard activity. Trigger record or playback accordingly.
prints "Press 'r' to record, 'p' for playback.\\n"
iTableLen = ftlen(giBuffer) ; derive buffer function table length
idur = iTableLen / sr ; derive storage time in seconds
kKey sensekey ; sense activity on the computer keyboard
if kKey=114 then ; if ASCCI value of 114 ('r') is output
event "i", 2, 0, idur, iTableLen ; activate recording instrument (2)
endif
if kKey=112 then ; if ASCCI value of 112 ('p) is output
event "i", 3, 0, idur, iTableLen ; activate playback instrument
endif
endin
instr 2 ; record to buffer
iTableLen = p4 ; table/recording length in samples
; -- print progress information to terminal --
prints "recording"
printks ".", 0.25 ; print '.' every quarter of a second
krelease release ; sense when note is in final k-rate pass...
if krelease=1 then ; then ..
printks "\\ndone\\n", 0 ; ... print a message
endif
; -- write audio to table --
ain inch 1 ; read audio from live input channel 1
andx line 0,p3,iTableLen ; create an index for writing to table
tablew ain,andx,giBuffer ; write audio to function table
endin
instr 3 ; playback from buffer
iTableLen = p4 ; table/recording length in samples
; -- print progress information to terminal --
prints "playback"
printks ".", 0.25 ; print '.' every quarter of a second
krelease release ; sense when note is in final k-rate pass
if krelease=1 then ; then ...
printks "\\ndone\\n", 0 ; ... print a message
endif; end of conditional branch
; -- read audio from table --
aNdx line 0, p3, iTableLen; create an index for reading from table
a1 table aNdx, giBuffer ; read audio to audio storage table
out a1 ; send audio to output
endin
</CsInstruments>
<CsScore>
i 1 0 3600 ; Sense keyboard activity. Start recording - playback.
</CsScore>
</CsoundSynthesizer>
Encapsulating Record and Play Buffer Functionality to a UDO
Recording and playing back of buffers can also be encapsulated into a User Defined Opcode. This time the tabw opcode will be used for writing audio data to a buffer. tabw is slightly faster than tablew but doesn't offer the same number of protections for out of range index values.
An empty table (buffer) of any size can be created with a negative number as size. A table for recording 10 seconds of audio data can be created in this way:
giBuf1 ftgen 0, 0, -(10*sr), 2, 0
The user can decide whether they want to assign a certain number to the table, or whether to allow Csound do assign one automatically, thereafter calling the table via its variable name, in this case giBuf1. Below follows a UDO for creating a mono buffer, and another UDO for creating a stereo buffer:
opcode BufCrt1, i, io ilen, inum xin ift ftgen inum, 0, -(ilen*sr), 2, 0 xout ift endop opcode BufCrt2, ii, io ilen, inum xin iftL ftgen inum, 0, -(ilen*sr), 2, 0 iftR ftgen inum, 0, -(ilen*sr), 2, 0 xout iftL, iftR endop
This simplifies the procedure of creating a record/play buffer, because the user is just asked for the length of the buffer. A number can be given, but by default Csound will assign this number. This statement will create an empty stereo table for 5 seconds of recording:
iBufL,iBufR BufCrt2 5
A first, simple version of a UDO for recording will just write the incoming audio to sequential locations of the table. This can be done by setting the ksmps value to 1 inside this UDO (setksmps 1), so that each audio sample has its own discrete k-value. In this way the write index for the table can be assigned via the statement andx=kndx, and increased by one for the next k-cycle. An additional k-input turns recording on and off:
opcode BufRec1, 0, aik ain, ift, krec xin setksmps 1 if krec == 1 then ;record as long as krec=1 kndx init 0 andx = kndx tabw ain, andx, ift kndx = kndx+1 endif endop
The reading procedure is just as simple. In fact the same code can be used; it will be sufficient just to replace the opcode for writing (tabw) with the opcode for reading (tab):
opcode BufPlay1, a, ik ift, kplay xin setksmps 1 if kplay == 1 then ;play as long as kplay=1 kndx init 0 andx = kndx aout tab andx, ift kndx = kndx+1 endif endop
Next we will use these first simple UDOs in a Csound instrument. Press the "r" key as long as you want to record, and the "p" key for playing back. Note that you must disable the key repeats on your computer keyboard for this example (in QuteCsound, disable "Allow key repeats" in Configuration -> General).
EXAMPLE 06B04_BufRecPlay_UDO.csd
<CsoundSynthesizer>
<CsOptions>
-i adc -o dac -d -m0
</CsOptions>
<CsInstruments>
;example written by Joachim Heintz
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
opcode BufCrt1, i, io
ilen, inum xin
ift ftgen inum, 0, -(ilen*sr), 2, 0
xout ift
endop
opcode BufRec1, 0, aik
ain, ift, krec xin
setksmps 1
imaxindx = ftlen(ift)-1 ;max index to write
knew changed krec
if krec == 1 then ;record as long as krec=1
if knew == 1 then ;reset index if restarted
kndx = 0
endif
kndx = (kndx > imaxindx ? imaxindx : kndx)
andx = kndx
tabw ain, andx, ift
kndx = kndx+1
endif
endop
opcode BufPlay1, a, ik
ift, kplay xin
setksmps 1
imaxindx = ftlen(ift)-1 ;max index to read
knew changed kplay
if kplay == 1 then ;play as long as kplay=1
if knew == 1 then ;reset index if restarted
kndx = 0
endif
kndx = (kndx > imaxindx ? imaxindx : kndx)
andx = kndx
aout tab andx, ift
kndx = kndx+1
endif
xout aout
endop
opcode KeyStay, k, kkk
;returns 1 as long as a certain key is pressed
key, k0, kascii xin ;ascii code of the key (e.g. 32 for space)
kprev init 0 ;previous key value
kout = (key == kascii || (key == -1 && kprev == kascii) ? 1 : 0)
kprev = (key > 0 ? key : kprev)
kprev = (kprev == key && k0 == 0 ? 0 : kprev)
xout kout
endop
opcode KeyStay2, kk, kk
;combines two KeyStay UDO's (this way is necessary
;because just one sensekey opcode is possible in an orchestra)
kasci1, kasci2 xin ;two ascii codes as input
key,k0 sensekey
kout1 KeyStay key, k0, kasci1
kout2 KeyStay key, k0, kasci2
xout kout1, kout2
endop
instr 1
ain inch 1 ;audio input on channel 1
iBuf BufCrt1 3 ;buffer for 3 seconds of recording
kRec,kPlay KeyStay2 114, 112 ;define keys for record and play
BufRec1 ain, iBuf, kRec ;record if kRec=1
aout BufPlay1 iBuf, kPlay ;play if kPlay=1
out aout ;send out
endin
</CsInstruments>
<CsScore>
i 1 0 1000
</CsScore>
</CsoundSynthesizer>
Next we will create an extended and easier to use version of these two UDOs for recording and playing back a buffer. The requirements of a user might be the following:
Recording:
- allow recording not just from the beginning of the buffer, but also from any arbitrary starting point kstart
- allow circular recording (wrap around) if the end of the buffer has been reached: kwrap=1
Playing:
- play back with different speed kspeed (negative speed means playing backwards)
- start playback at any point of the buffer kstart
- end playback at any point of the buffer kend
- allow certain modes of wraparound kwrap while playing:
- kwrap=0 stops at the defined end point of the buffer
- kwrap=1 repeats playback between defined end and start points
- kwrap=2 starts at a defined starting point but wraps between end point and beginning of the buffer
- kwrap=3 wraps between kstart and the end of the table
The following example provides versions of BufRec and BufPlay which do this job. We will use the table3 opcode instead of the simple tab or table opcodes in this case, because we want to translate any number of samples in the table to any number of output samples using different speed values. In short, we will need to read amplitude values that must be 'imagined' between two existing table value.
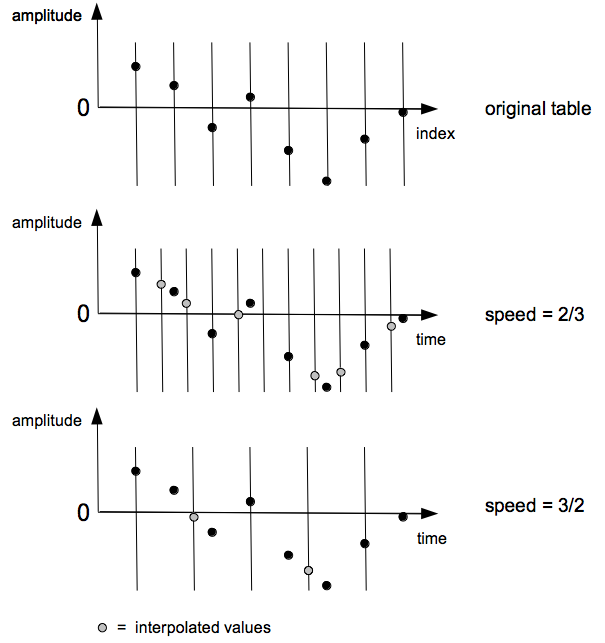
For higher or lower speed values than the original record speed, interpolation must be used in between certain sample values if the original shape of the wave is to be reproduced as accurately as possible. This job is performed with high quality by table3 which employs cubic interpolation.
In a typical application of recording and playing buffer buffers, the ability to interact with the process will be paramount. We can benefit from having interactive access to the following:
- starting and stopping record
- adjusting the start and end points of recording
- use or prevent wraparound while recording
- starting and stopping playback
- adjusting the start and end points of playback
- adjusting wraparound in playback using one of the specified modes (1 - 4)
- applying volume control to the playback signal
These interactions could be carried out via widgets, MIDI, OSC or something else. As we want to provide examples which can be used with any Csound frontend here, we are restricted to triggering the record and play events by hitting the space bar of the computer keyboard. (See the CsoundQt version of this example for a more interactive version.)
EXAMPLE 06B05_BufRecPlay_complex.csd
<CsoundSynthesizer>
<CsOptions>
-i adc -o dac -d
</CsOptions>
<CsInstruments>
;example written by joachim heintz
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
opcode BufCrt2, ii, io ;creates a stereo buffer
ilen, inum xin ;ilen = length of the buffer (table) in seconds
iftL ftgen inum, 0, -(ilen*sr), 2, 0
iftR ftgen inum, 0, -(ilen*sr), 2, 0
xout iftL, iftR
endop
opcode BufRec1, k, aikkkk ;records to a buffer
ain, ift, krec, kstart, kend, kwrap xin
setksmps 1
kendsmps = kend*sr ;end point in samples
kendsmps = (kendsmps == 0 || kendsmps > ftlen(ift) ? ftlen(ift) : kendsmps)
kfinished = 0
knew changed krec ;1 if record just started
if krec == 1 then
if knew == 1 then
kndx = kstart * sr - 1 ;first index to write
endif
if kndx >= kendsmps-1 && kwrap == 1 then
kndx = -1
endif
if kndx < kendsmps-1 then
kndx = kndx + 1
andx = kndx
tabw ain, andx, ift
else
kfinished = 1
endif
endif
xout kfinished
endop
opcode BufRec2, k, aaiikkkk ;records to a stereo buffer
ainL, ainR, iftL, iftR, krec, kstart, kend, kwrap xin
kfin BufRec1 ainL, iftL, krec, kstart, kend, kwrap
kfin BufRec1 ainR, iftR, krec, kstart, kend, kwrap
xout kfin
endop
opcode BufPlay1, ak, ikkkkkk
ift, kplay, kspeed, kvol, kstart, kend, kwrap xin
;kstart = begin of playing the buffer in seconds
;kend = end of playing in seconds. 0 means the end of the table
;kwrap = 0: no wrapping. stops at kend (positive speed) or kstart
; (negative speed).this makes just sense if the direction does not
; change and you just want to play the table once
;kwrap = 1: wraps between kstart and kend
;kwrap = 2: wraps between 0 and kend
;kwrap = 3: wraps between kstart and end of table
;CALCULATE BASIC VALUES
kfin init 0
iftlen = ftlen(ift)/sr ;ftlength in seconds
kend = (kend == 0 ? iftlen : kend) ;kend=0 means end of table
kstart01 = kstart/iftlen ;start in 0-1 range
kend01 = kend/iftlen ;end in 0-1 range
kfqbas = (1/iftlen) * kspeed ;basic phasor frequency
;DIFFERENT BEHAVIOUR DEPENDING ON WRAP:
if kplay == 1 && kfin == 0 then
;1. STOP AT START- OR ENDPOINT IF NO WRAPPING REQUIRED (kwrap=0)
if kwrap == 0 then
; -- phasor freq so that 0-1 values match distance start-end
kfqrel = kfqbas / (kend01-kstart01)
andxrel phasor kfqrel ;index 0-1 for distance start-end
; -- final index for reading the table (0-1)
andx = andxrel * (kend01-kstart01) + (kstart01)
kfirst init 1 ;don't check condition below at the first k-cycle (always true)
kndx downsamp andx
kprevndx init 0
;end of table check:
;for positive speed, check if this index is lower than the previous one
if kfirst == 0 && kspeed > 0 && kndx < kprevndx then
kfin = 1
;for negative speed, check if this index is higher than the previous one
else
kprevndx = (kprevndx == kstart01 ? kend01 : kprevndx)
if kfirst == 0 && kspeed < 0 && kndx > kprevndx then
kfin = 1
endif
kfirst = 0 ;end of first cycle in wrap = 0
endif
;sound out if end of table has not yet reached
asig table3 andx, ift, 1
kprevndx = kndx ;next previous is this index
;2. WRAP BETWEEN START AND END (kwrap=1)
elseif kwrap == 1 then
kfqrel = kfqbas / (kend01-kstart01) ;same as for kwarp=0
andxrel phasor kfqrel
andx = andxrel * (kend01-kstart01) + (kstart01)
asig table3 andx, ift, 1 ;sound out
;3. START AT kstart BUT WRAP BETWEEN 0 AND END (kwrap=2)
elseif kwrap == 2 then
kw2first init 1
if kw2first == 1 then ;at first k-cycle:
reinit wrap3phs ;reinitialize for getting the correct start phase
kw2first = 0
endif
kfqrel = kfqbas / kend01 ;phasor freq so that 0-1 values match distance start-end
wrap3phs:
andxrel phasor kfqrel, i(kstart01) ;index 0-1 for distance start-end
rireturn ;end of reinitialization
andx = andxrel * kend01 ;final index for reading the table
asig table3 andx, ift, 1 ;sound out
;4. WRAP BETWEEN kstart AND END OF TABLE(kwrap=3)
elseif kwrap == 3 then
kfqrel = kfqbas / (1-kstart01) ;phasor freq so that 0-1 values match distance start-end
andxrel phasor kfqrel ;index 0-1 for distance start-end
andx = andxrel * (1-kstart01) + kstart01 ;final index for reading the table
asig table3 andx, ift, 1
endif
else ;if either not started or finished at wrap=0
asig = 0 ;don't produce any sound
endif
xout asig*kvol, kfin
endop
opcode BufPlay2, aak, iikkkkkk ;plays a stereo buffer
iftL, iftR, kplay, kspeed, kvol, kstart, kend, kwrap xin
aL,kfin BufPlay1 iftL, kplay, kspeed, kvol, kstart, kend, kwrap
aR,kfin BufPlay1 iftR, kplay, kspeed, kvol, kstart, kend, kwrap
xout aL, aR, kfin
endop
opcode In2, aa, kk ;stereo audio input
kchn1, kchn2 xin
ain1 inch kchn1
ain2 inch kchn2
xout ain1, ain2
endop
opcode Key, kk, k
;returns '1' just in the k-cycle a certain key has been pressed (kdown)
; or released (kup)
kascii xin ;ascii code of the key (e.g. 32 for space)
key,k0 sensekey
knew changed key
kdown = (key == kascii && knew == 1 && k0 == 1 ? 1 : 0)
kup = (key == kascii && knew == 1 && k0 == 0 ? 1 : 0)
xout kdown, kup
endop
instr 1
giftL,giftR BufCrt2 3 ;creates a stereo buffer for 3 seconds
gainL,gainR In2 1,2 ;read input channels 1 and 2 and write as global audio
prints "PLEASE PRESS THE SPACE BAR ONCE AND GIVE AUDIO INPUT
ON CHANNELS 1 AND 2.\n"
prints "AUDIO WILL BE RECORDED AND THEN AUTOMATICALLY PLAYED
BACK IN SEVERAL MANNERS.\n"
krec,k0 Key 32
if krec == 1 then
event "i", 2, 0, 10
endif
endin
instr 2
; -- records the whole buffer and returns 1 at the end
kfin BufRec2 gainL, gainR, giftL, giftR, 1, 0, 0, 0
if kfin == 0 then
printks "Recording!\n", 1
endif
if kfin == 1 then
ispeed random -2, 2
istart random 0, 1
iend random 2, 3
iwrap random 0, 1.999
iwrap = int(iwrap)
printks "Playing back with speed = %.3f, start = %.3f, end = %.3f,
wrap = %d\n", p3, ispeed, istart, iend, iwrap
aL,aR,kf BufPlay2 giftL, giftR, 1, ispeed, 1, istart, iend, iwrap
if kf == 0 then
printks "Playing!\n", 1
endif
endif
krel release
if kfin == 1 && kf == 1 || krel == 1 then
printks "PRESS SPACE BAR AGAIN!\n", p3
turnoff
endif
outs aL, aR
endin
</CsInstruments>
<CsScore>
i 1 0 1000
e
</CsScore>
</CsoundSynthesizer>
Further Opcodes for Investigation
Csound contains a wide range of opcodes that offer a variety of 'ready-made' methods of playing back audio held in a function table. The oldest group of these opcodes are loscil and loscil3. Despite their age they offer some unique features such as the ability implement both sustain and release stage looping (in a variety of looping modes), their ability to read from stereo as well as mono function tables and their ability to read looping and base frequency data from the sound file stored in the function table. loscil and loscil3 were originally intended as the kernel mechanism for building a sampler.
For reading multichannel files of more than two channels, the more recent loscilx exists as an option.
loscil and loscil3 will only allow looping points to be defined at i-time. lposcil, lposcil3, lposcila, lposcilsa and lposcilsa2 will allow looping points to be changed a k-rate, while the note is playing.
It is worth not forgetting Csound's more exotic methods of playback of sample stored in function tables. mincer and temposcal use streaming vocoder techniques to faciliate independent pitch and time-stretch control during playback (this area is covered more fully in the chapter FOURIER ANALYSIS / SPECTRAL PROCESSING. sndwarp and sndwarpst similiarly faciliate independent pitch and playback speed control but through the technique of granular synthesis this area is covered in detail in the chapter GRANULAR SYNTHESIS.
07 MIDI
RECEIVING EVENTS BY MIDIIN
Csound provides a variety of opcodes, such as cpsmidi, ampmidi and ctrl7, which facilitate the reading of incoming midi data into Csound with minimal fuss. These opcodes allow us to read in midi information without us having to worry about parsing status bytes and so on. Occasionally though when more complex midi interaction is required, it might be advantageous for us to scan all raw midi information that is coming into Csound. The midiin opcode allows us to do this.
In the next example a simple midi monitor is constructed. Incoming midi events are printed to the terminal with some formatting to make them readable. We can disable Csound's default instrument triggering mechanism (which in this example we don't want to use) by writing the line:
massign 0,0
just after the header statement (sometimes referred to as instrument 0).
For this example to work you will need to ensure that you have activated live midi input within Csound, either by using the -M flag or from within the QuteCsound configuration menu. You will also need to make sure that you have a midi keyboard or controller connected. You may also want to include the -m0 flag which will disable some of Csound's additional messaging output and therefore allow our midi printout to be presented more clearly.
The status byte tells us what sort of midi information has been received. For example, a value of 144 tells us that a midi note event has been received, a value of 176 tells us that a midi controller event has been received, a value of 224 tells us that pitch bend has been received and so on.
The meaning of the two data bytes depends on what sort of status byte has been received. For example if a midi note event has been received then data byte 1 gives us the note velocity and data byte 2 gives us the note number. If a midi controller event has been received then data byte 1 gives us the controller number and data byte 2 gives us the controller value.
EXAMPLE 07A01_midiin_print.csd
<CsoundSynthesizer>
<CsOptions>
-Ma -m0
; activates all midi devices, suppress note printings
</CsOptions>
<CsInstruments>
; Example by Iain McCurdy
; no audio so 'sr' or 'nchnls' aren't relevant
ksmps = 32
; using massign with these arguments disables default instrument triggering
massign 0,0
instr 1
kstatus, kchan, kdata1, kdata2 midiin ;read in midi
ktrigger changed kstatus, kchan, kdata1, kdata2 ;trigger if midi data changes
if ktrigger=1 && kstatus!=0 then ;if status byte is non-zero...
; -- print midi data to the terminal with formatting --
printks "status:%d%tchannel:%d%tdata1:%d%tdata2:%d%n"\
,0,kstatus,kchan,kdata1,kdata2
endif
endin
</CsInstruments>
<CsScore>
i 1 0 3600 ; instr 1 plays for 1 hour
</CsScore>
</CsoundSynthesizer>
The principle advantage of using the midiin opcode is that, unlike opcodes such as cpsmidi, ampmidi and ctrl7 which only receive specific midi data types on a specific channel, midiin 'listens' to all incoming data including system exclusive messages. In situations where elaborate Csound instrument triggering mappings that are beyond the capabilities of the default triggering mechanism are required, then the use of midiin might be beneficial.
TRIGGERING INSTRUMENT INSTANCES
Csound's Default System of Instrument Triggering Via Midi
Csound has a default system for instrument triggering via midi. Provided a midi keyboard has been connected and the appropriate command line flags for midi input have been set (see configuring midi for further information) or the appropriate settings have been made in QuteCsound's configuration menu, then midi notes received on midi channel 1 will trigger instrument 1, notes on channel 2 will trigger instrument 2 and so on. Instruments will turn on and off in sympathy with notes being pressed and released on the midi keyboard and Csound will correctly unravel polyphonic layering and turn on and off only the correct layer of the same instrument begin played. Midi activated notes can be thought of as 'held' notes, similar to notes activated in the score with a negative duration (p3). Midi activated notes will sustain indefinitely as long as the performance time will allow until a corresponding note off has been received - this is unless this infinite p3 duration is overwritten within the instrument itself by p3 begin explicitly defined.
The following example confirms this default mapping of midi channels to instruments. You will need a midi keyboard that allows you to change the midi channel on which it is transmmitting. Besides a written confirmation to the console of which instrument is begin triggered, there is an audible confirmation in that instrument 1 plays single pulses, instrument 2 plays sets of two pulses and instrument 3 plays sets of three pulses. The example does not go beyond three instruments. If notes are received on midi channel 4 and above, because corresonding instruments do not exist, notes on any of these channels will be directed to instrument 1.
EXAMPLE 07B01_MidiInstrTrigger.csd
<CsoundSynthesizer>
<CsOptions>
-Ma -odac -m0
;activates all midi devices, real time sound output, and suppress note printings
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
gisine ftgen 0,0,2^12,10,1
instr 1 ; 1 impulse (midi channel 1)
prints "instrument/midi channel: %d%n",p1 ; print instrument number to terminal
reset: ; label 'reset'
timout 0, 1, impulse ; jump to 'impulse' for 1 second
reinit reset ; reninitialise pass from 'reset'
impulse: ; label 'impulse'
aenv expon 1, 0.3, 0.0001 ; a short percussive envelope
aSig poscil aenv, 500, gisine ; audio oscillator
out aSig ; audio to output
endin
instr 2 ; 2 impulses (midi channel 2)
prints "instrument/midi channel: %d%n",p1
reset:
timout 0, 1, impulse
reinit reset
impulse:
aenv expon 1, 0.3, 0.0001
aSig poscil aenv, 500, gisine
a2 delay aSig, 0.15 ; short delay adds another impulse
out aSig+a2 ; mix two impulses at output
endin
instr 3 ; 3 impulses (midi channel 3)
prints "instrument/midi channel: %d%n",p1
reset:
timout 0, 1, impulse
reinit reset
impulse:
aenv expon 1, 0.3, 0.0001
aSig poscil aenv, 500, gisine
a2 delay aSig, 0.15 ; delay adds a 2nd impulse
a3 delay a2, 0.15 ; delay adds a 3rd impulse
out aSig+a2+a3 ; mix the three impulses at output
endin
</CsInstruments>
<CsScore>
f 0 300
e
</CsScore>
<CsoundSynthesizer>
Using massign to Map MIDI Channels to Instruments
We can use the massign opcode, which is used just after the header statement, to explicitly map midi channels to specific instruments and thereby overrule Csound's default mappings. massign takes two input arguments, the first defines the midi channel to be redirected and the second defines which instrument it should be directed to. The following example is identical to the previous one except that the massign statements near the top of the orchestra jumbles up the default mappings. Midi notes on channel 1 will be mapped to instrument 3, notes on channel 2 to instrument 1 and notes on channel 3 to instrument 2. Undefined channel mappings will be mapped according to the default arrangement and once again midi notes on channels for which an instrument does not exist will be mapped to instrument 1.
EXAMPLE 07B02_massign.csd
<CsoundSynthesizer>
<CsOptions>
-Ma -odac -m0
; activate all midi devices, real time sound output, and suppress note printing
</CsOptions>
<CsInstruments>
; Example by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
gisine ftgen 0,0,2^12,10,1
massign 1,3 ; channel 1 notes directed to instr 3
massign 2,1 ; channel 2 notes directed to instr 1
massign 3,2 ; channel 3 notes directed to instr 2
instr 1 ; 1 impulse (midi channel 1)
iChn midichn ; discern what midi channel
prints "channel:%d%tinstrument: %d%n",iChn,p1 ; print instr num and midi channel
reset: ; label 'reset'
timout 0, 1, impulse ; jump to 'impulse' for 1 second
reinit reset ; reninitialize pass from 'reset'
impulse: ; label 'impulse'
aenv expon 1, 0.3, 0.0001 ; a short percussive envelope
aSig poscil aenv, 500, gisine ; audio oscillator
out aSig ; send audio to output
endin
instr 2 ; 2 impulses (midi channel 2)
iChn midichn
prints "channel:%d%tinstrument: %d%n",iChn,p1
reset:
timout 0, 1, impulse
reinit reset
impulse:
aenv expon 1, 0.3, 0.0001
aSig poscil aenv, 500, gisine
a2 delay aSig, 0.15 ; delay generates a 2nd impulse
out aSig+a2 ; mix two impulses at the output
endin
instr 3 ; 3 impulses (midi channel 3)
iChn midichn
prints "channel:%d%tinstrument: %d%n",iChn,p1
reset:
timout 0, 1, impulse
reinit reset
impulse:
aenv expon 1, 0.3, 0.0001
aSig poscil aenv, 500, gisine
a2 delay aSig, 0.15 ; delay generates a 2nd impulse
a3 delay a2, 0.15 ; delay generates a 3rd impulse
out aSig+a2+a3 ; mix three impulses at output
endin
</CsInstruments>
<CsScore>
f 0 300
e
</CsScore>
<CsoundSynthesizer>
massign also has a couple of additional functions that may come in useful. A channel number of zero is interpreted as meaning 'any'. The following instruction will map notes on any and all channels to instrument 1.
massign 0,1
An instrument number of zero is interpreted as meaning 'none' so the following instruction will instruct Csound to ignore triggering for notes received on all channels.
massign 0,0
The above feature is useful when we want to scan midi data from an already active instrument using the midiin opcode, as we did in EXAMPLE 0701.csd.
Using Multiple Triggering
Csound's event/event_i opcode (see the Triggering Instrument Events chapter) makes it possible to trigger any other instrument from a midi-triggered one. As you can assign a fractional number to an instrument, you can distinguish the single instances from each other. Below is an example of using fractional instrument numbers.
EXAMPLE 07B03_MidiTriggerChain.csd
<CsoundSynthesizer>
<CsOptions>
-Ma
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz, using code of Victor Lazzarini
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
massign 0, 1 ;assign all incoming midi to instr 1
instr 1 ;global midi instrument, calling instr 2.cc.nnn
;(c=channel, n=note number)
inote notnum ;get midi note number
ichn midichn ;get midi channel
instrnum = 2 + ichn/100 + inote/100000 ;make fractional instr number
; -- call with indefinite duration
event_i "i", instrnum, 0, -1, ichn, inote
kend release ;get a "1" if instrument is turned off
if kend == 1 then
event "i", -instrnum, 0, 1 ;then turn this instance off
endif
endin
instr 2
ichn = int(frac(p1)*100)
inote = round(frac(frac(p1)*100)*1000)
prints "instr %f: ichn = %f, inote = %f%n", p1, ichn, inote
printks "instr %f playing!%n", 1, p1
endin
</CsInstruments>
<CsScore>
f 0 36000
e
</CsScore>
</CsoundSynthesizer>
This example merely demonstrates a technique for passing information about MIDI channel and note number from the directly triggered instrument to a sub-instrument. A practical application for this would be for creating keygroups - triggering different instruments by playing in different regions of the keyboard. In this case you could change just the line:
instrnum = 2 + ichn/100 + inote/100000
to this:
if inote < 48 then
instrnum = 2 elseif inote < 72 then instrnum = 3 else instrnum = 4 endif instrnum = instrnum + ichn/100 + inote/100000
In this case for any key below C3 instrument 2 will be called, for any key between C3 and B4 instrument 3, and for any higher key instrument 4.
Using this multiple triggering you are also able to trigger more than one instrument at the same time (which is not possible using the massign opcode). Here is an example using a user defined opcode (see the UDO chapter of this manual):
EXAMPLE 07B04_MidiMultiTrigg.csd
<CsoundSynthesizer>
<CsOptions>
-Ma
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz, using code of Victor Lazzarini
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
massign 0, 1 ;assign all incoming midi to instr 1
giInstrs ftgen 0, 0, -5, -2, 2, 3, 4, 10, 100 ;instruments to be triggered
opcode MidiTrig, 0, io
;triggers the first inum instruments in the function table ifn by a midi event,
; with fractional numbers containing channel and note number information
; -- if inum=0 or not given, all instrument numbers in ifn are triggered
ifn, inum xin
inum = (inum == 0 ? ftlen(ifn) : inum)
inote notnum
ichn midichn
iturnon = 0
turnon:
iinstrnum tab_i iturnon, ifn
if iinstrnum > 0 then
ifracnum = iinstrnum + ichn/100 + inote/100000
event_i "i", ifracnum, 0, -1
endif
loop_lt iturnon, 1, inum, turnon
kend release
if kend == 1 then
kturnoff = 0
turnoff:
kinstrnum tab kturnoff, ifn
if kinstrnum > 0 then
kfracnum = kinstrnum + ichn/100 + inote/100000
event "i", -kfracnum, 0, 1
loop_lt kturnoff, 1, inum, turnoff
endif
endif
endop
instr 1 ;global midi instrument
; -- trigger the first two instruments in the giInstrs table
MidiTrig giInstrs, 2
endin
instr 2
ichn = int(frac(p1)*100)
inote = round(frac(frac(p1)*100)*1000)
prints "instr %f: ichn = %f, inote = %f%n", p1, ichn, inote
printks "instr %f playing!%n", 1, p1
endin
instr 3
ichn = int(frac(p1)*100)
inote = round(frac(frac(p1)*100)*1000)
prints "instr %f: ichn = %f, inote = %f%n", p1, ichn, inote
printks "instr %f playing!%n", 1, p1
endin
</CsInstruments>
<CsScore>
f 0 36000
e
</CsScore>
</CsoundSynthesizer>
WORKING WITH CONTROLLERS
Scanning MIDI Continuous Controllers
The most useful opcode for reading in midi continuous controllers is ctrl7. ctrl7's input arguments allow us to specify midi channel and controller number of the controller to be scanned in addition to giving us the option of rescaling the received midi values between a new minimum and maximum value as defined by the 3rd and 4th input arguments. Further possibilities for modifying the data output are provided by the 5th (optional) argument which is used to point to a function table that reshapes the controller's output response to something possibly other than linear. This can be useful when working with parameters which are normally expressed on a logarithmic scale such as frequency.
The following example scans midi controller 1 on channel 1 and prints values received to the console. The minimum and maximum values are given as 0 and 127 therefore they are not rescaled at all. Controller 1 is also the modulation wheel on a midi keyboard.
EXAMPLE 07C01_ctrl7_print.csd
<CsoundSynthesizer>
<CsOptions>
-Ma -odac
; activate all MIDI devices
</CsOptions>
<CsInstruments>
; 'sr' and 'nchnls' are irrelevant so are omitted
ksmps = 32
instr 1
kCtrl ctrl7 1,1,0,127 ; read in controller 1 on channel 1
kTrigger changed kCtrl ; if 'kCtrl' changes generate a trigger ('bang')
if kTrigger=1 then
; Print kCtrl to console with formatting, but only when its value changes.
printks "Controller Value: %d%n", 0, kCtrl
endif
endin
</CsInstruments>
<CsScore>
i 1 0 3600
e
</CsScore>
<CsoundSynthesizer>
There are also 14 bit and 21 bit versions of ctrl7 (ctrl14 and ctrl21) which improve upon the 7 bit resolution of 'ctrl7' but hardware that outputs 14 or 21 bit controller information is rare so these opcodes are seldom used.
Scanning Pitch Bend and Aftertouch
We can scan pitch bend and aftertouch in a similar way by using the opcodes pchbend and aftouch. Once again we can specify minimum and maximum values with which to rescale the output. In the case of 'pchbend' we specify the value it outputs when the pitch bend wheel is at rest followed by a value which defines the entire range from when it is pulled to its minimum to when it is pushed to its maximum. In this example, playing a key on the keyboard will play a note, the pitch of which can be bent up or down two semitones by using the pitch bend wheel. Aftertouch can be used to modify the amplitude of the note while it is playing. Pitch bend and aftertouch data is also printed at the terminal whenever they change. One thing to bear in mind is that for 'pchbend' to function the Csound instrument that contains it needs to have been activated by a MIDI event, i.e. you will need to play a midi note on your keyboard and then move the pitch bend wheel.
EXAMPLE 07C02_pchbend_aftouch.csd
<CsoundSynthesizer>
<CsOptions>
-odac -Ma
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giSine ftgen 0,0,2^10,10,1 ; a sine wave
instr 1
; -- pitch bend --
kPchBnd pchbend 0,4 ; read in pitch bend (range -2 to 2)
kTrig1 changed kPchBnd ; if 'kPchBnd' changes generate a trigger
if kTrig1=1 then
printks "Pitch Bend:%f%n",0,kPchBnd ; print kPchBnd to console when it changes
endif
; -- aftertouch --
kAfttch aftouch 0,0.9 ; read in aftertouch (range 0 to 0.9)
kTrig2 changed kAfttch ; if 'kAfttch' changes generate a trigger
if kTrig2=1 then
printks "Aftertouch:%d%n",0,kAfttch ; print kAfttch to console when it changes
endif
; -- create a sound --
iNum notnum ; read in MIDI note number
; MIDI note number + pitch bend are converted to cycles per seconds
aSig poscil 0.1,cpsmidinn(iNum+kPchBnd),giSine
out aSig ; audio to output
endin
</CsInstruments>
<CsScore>
f 0 300
e
</CsScore>
<CsoundSynthesizer>
Initialising MIDI Controllers
It may be useful to be able to define the initial value of a midi controller, that is, the value any ctrl7s will adopt until their corresponding hardware controls have been moved. Midi hardware controls only send messages when they change so until this happens their values in Csound defaults to their minimum settings unless additional initialisation has been carried out. As an example, if we imagine we have a Csound instrument in which the output volume is controlled by a midi controller it might prove to be slightly frustrating that each time the orchestra is launched, this instrument will remain silent until the volume control is moved. This frustration might become greater when many midi controllers are begin utilised. It would be more useful to be able to define the starting value for each of these controllers. The initc7 opcode allows us to do this. If initc7 is placed within the instrument itself it will be reinitialised each time the instrument is called, if it is placed in instrument 0 (just after the header statements) then it will only be initialised when the orchestra is first launched. The latter case is probably most useful.
In the following example a simple synthesizer is created. Midi controller 1 controls the output volume of this instrument but the initc7 statement near the top of the orchestra ensures that this control does not default to its minimum setting. The arguments that initc7 takes are for midi channel, controller number and initial value. Initial value is defined within the range 0-1, therefore a value of 1 will set this controller to its maximum value (midi value 127), and a value of 0.5 will set it to its halfway value (midi value 64), and so on.
Additionally this example uses the cpsmidi opcode to scan midi pitch (basically converting midi note numbers to cycles-per-second) and the ampmidi opcode to scan and rescale key velocity.
EXAMPLE 07C03_cpsmidi_ampmidi.csd
<CsoundSynthesizer>
<CsOptions>
-Ma -odac
; activate all midi inputs and real-time audio output
</CsOptions>
<CsInstruments>
; Example by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giSine ftgen 0,0,2^12,10,1 ; a sine wave
initc7 1,1,1 ; initialize CC 1 on chan. 1 to its max level
instr 1
iCps cpsmidi ; read in midi pitch in cycles-per-second
iAmp ampmidi 1 ; read in key velocity. Rescale to be from 0 to 1
kVol ctrl7 1,1,0,1 ; read in CC 1, chan 1. Rescale to be from 0 to 1
aSig poscil iAmp*kVol, iCps, giSine ; an audio oscillator
out aSig ; send audio to output
endin
</CsInstruments>
<CsScore>
f 0 3600
e
</CsScore>
<CsoundSynthesizer>
You will maybe hear that this instrument produces 'clicks' as notes begin and end. To find out how to prevent this see the section on envelopes with release sensing in the chapter Sound Modification: Envelopes.
Smoothing 7-bit Quantisation in MIDI Controllers
A problem we encounter with 7 bit midi controllers is the poor resolution that they offer us. 7 bit means that we have 2 to the power of 7 possible values; therefore 128 possible values, which is rather inadequate for defining, for example, the frequency of an oscillator over a number of octaves, the cutoff frequency of a filter or a quickly moving volume control. We soon become aware of the parameter that is being changed moving in steps - so not really a 'continuous' controller. We may also experience clicking artefacts, sometimes called 'zipper noise', as the value changes. The extent of this will depend upon the parameter being controlled. There are some things we can do to address this problem. We can filter the controller signal within Csound so that the sudden changes that occur between steps along the controller's travel are smoothed using additional interpolating values - we must be careful not to smooth excessively otherwise the response of the controller will become sluggish. Any k-rate compatible lowpass filter can be used for this task but the portk opcode is particularly useful as it allows us to define the amount of smoothing as a time taken to glide to half the required value rather than having to specify a cutoff frequency. Additionally this 'half time' value can be varied at k-rate which provides an advantage availed of in the following example.
This example takes the simple synthesizer of the previous example as its starting point. The volume control, which is controlled by midi controller 1 on channel 1, is passed through a 'portk' filter. The 'half time' for 'portk' ramps quickly up to its required value of 0.01 through the use of a linseg statement in the previous line. This ensures that when a new note begins the volume control immediately jumps to its required value rather than gliding up from zero as would otherwise be affected by the 'portk' filter. Try this example with the 'portk' half time defined as a constant to hear the difference. To further smooth the volume control, it is converted to an a-rate variable through the use of the interp opcode which, as well as performing this conversion, interpolates values in the gaps between k-cycles.
EXAMPLE 07C04_smoothing.csd
<CsoundSynthesizer>
<CsOptions>
-Ma -odac
</CsOptions>
<CsInstruments>
;Example by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giSine ftgen 0,0,2^12,10,1
initc7 1,1,1 ; initialize CC 1 to its max. level
instr 1
iCps cpsmidi ; read in midi pitch in cycles-per-second
iAmp ampmidi 1 ; read in note velocity - re-range 0 to 1
kVol ctrl7 1,1,0,1 ; read in CC 1, chan. 1. Re-range from 0 to 1
kPortTime linseg 0,0.001,0.01 ; create a value that quickly ramps up to 0.01
kVol portk kVol,kPortTime ; create a filtered version of kVol
aVol interp kVol ; create an a-rate version of kVol
aSig poscil iAmp*aVol,iCps,giSine
out aSig
endin
</CsInstruments>
<CsScore>
f 0 300
e
</CsScore>
<CsoundSynthesizer>
All of the techniques introduced in this section are combined in the final example which includes a 2-semitone pitch bend and tone control which is controlled by aftertouch. For tone generation this example uses the gbuzz opcode.
EXAMPLE 07C05_MidiControlComplex.csd
<CsoundSynthesizer>
<CsOptions>
-Ma -odac
</CsOptions>
<CsInstruments>
;Example by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
giCos ftgen 0,0,2^12,11,1 ; a cosine wave
initc7 1,1,1 ; initialize controller to its maximum level
instr 1
iNum notnum ; read in midi note number
iAmp ampmidi 0.1 ; read in note velocity - range 0 to 0.2
kVol ctrl7 1,1,0,1 ; read in CC 1, chan. 1. Re-range from 0 to 1
kPortTime linseg 0,0.001,0.01 ; create a value that quickly ramps up to 0.01
kVol portk kVol, kPortTime ; create filtered version of kVol
aVol interp kVol ; create an a-rate version of kVol.
iRange = 2 ; pitch bend range in semitones
iMin = 0 ; equilibrium position
kPchBnd pchbend iMin, 2*iRange ; pitch bend in semitones (range -2 to 2)
kPchBnd portk kPchBnd,kPortTime; create a filtered version of kPchBnd
aEnv linsegr 0,0.005,1,0.1,0 ; amplitude envelope with release stage
kMul aftouch 0.4,0.85 ; read in aftertouch
kMul portk kMul,kPortTime ; create a filtered version of kMul
; create an audio signal using the 'gbuzz' additive synthesis opcode
aSig gbuzz iAmp*aVol*aEnv,cpsmidinn(iNum+kPchBnd),70,0,kMul,giCos
out aSig ; audio to output
endin
</CsInstruments>
<CsScore>
f 0 300
e
</CsScore>
<CsoundSynthesizer>
RECORDING CONTROLLER DATA
Data performed on a controller or controllers can be recorded into GEN tables or arrays so that a real-time interaction with a Csound instrument can be replayed at a later time. This can be preferable to recording the audio output, as this will allow the controller data to be modified. The simplest approach is to simply store each controller value every k-cycle into sequential locations in a function table but this is rather wasteful as controllers will frequently remain unchanged from k-cycle to k-cycle.
A more efficient approach is to store values only when they change and to time stamp those events to that they can be replayed later on in the right order and at the right speed. In this case data will be written to a function table in pairs: time-stamp followed by a value for each new event ('event' refers to when a controller changes). This method does not store durations of each event, merely when they happen, therefore it will not record how long the final event lasts until recording stopped. This may or may not be critical depending on how the recorded controller data is used later on but in order to get around this, the following example stores the duration of the complete recording at index location 0 so that we can derive the duration of the last event. Additionally the first event stored at index location 1 is simply a value: the initial value of the controller (the time stamp for this would always be zero anyway). Thereafter events are stored as time-stamped pairs of data: index 2=time stamp, index 3=associated value and so on.
To use the following example, activate 'Record', move the slider around and then deactivate 'Record'. This gesture can now be replayed using the 'Play' button. As well as moving the GUI slider, a tone is produced, the pitch of which is controlled by the slider.
Recorded data in the GEN table can also be backed up onto the hard drive using ftsave and recalled in a later session using ftload. Note that ftsave also has the capability of storing multiple function tables in a single file.
EXAMPLE 07C06_RecordingController.csd
<CsoundSynthesizer>
<CsOptions>
-odac -dm0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 8
nchnls = 1
0dbfs = 1
FLpanel "Record Gesture",500,90,0,0
gkRecord,gihRecord FLbutton "Rec/Stop",1,0,22,100,25, 5, 5,-1
gkPlay,gihPlay FLbutton "Play", 1,0,22,100,25,110, 5,-1
gksave,ihsave FLbutton "Save to HD", 1,0,21,100,25,290,5,0,4,0,0
gkload,ihload FLbutton "Load from HD", 1,0,21,100,25,395,5,0,5,0,0
gkval, gihval FLslider "Control", 0,1, 0,23, -1,490,25, 5,35
FLpanel_end
FLrun
gidata ftgen 1,0,1048576,-2,0 ; Table for controller data.
opcode RecordController,0,Ki
kval,ifn xin
i_ ftgen 1,0,ftlen(ifn),-2,0 ; erase table
tableiw i(kval),1,ifn ; write initial value at index 1.
;(Index 0 will be used be storing the complete gesture duration.)
kndx init 2 ; Initialise index
kTime timeinsts ; time since this instrument started in seconds
; Write a data event only when the input value changes
if changed(kval)==1 && kndx<=(ftlen(ifn)-2) && kTime>0 then
; Write timestamp to table location defined by current index.
tablew kTime, kndx, ifn
; Write slider value to table location defined by current index.
tablew kval, kndx + 1, ifn
; Increment index 2 steps (one for time, one for value).
kndx = kndx + 2
endif
; sense note release
krel release
; if we are in the final k-cycle before the note ends
if(krel==1) then
; write total gesture duration into the table at index 0
tablew kTime,0,ifn
endif
endop
opcode PlaybackController,k,i
ifn xin
; read first value
; initial controller value read from index 1
ival table 1,ifn
; initial value for k-rate output
kval init ival
; Initialise index to first non-zero timestamp
kndx init 2
; time in seconds since this note started
kTime timeinsts
; first non-zero timestamp
iTimeStamp tablei 2,ifn
; initialise k-variable for first non-zero timestamp
kTimeStamp init iTimeStamp
; if we have reached the timestamp value...
if kTime>=kTimeStamp && kTimeStamp>0 then
; ...Read value from table defined by current index.
kval table kndx+1,ifn
kTimeStamp table kndx+2,ifn ; Read next timestamp
; Increment index. (Always 2 steps: timestamp and value.)
kndx limit kndx+2, 0, ftlen(ifn)-2
endif
xout kval
endop
; cleaner way to start instruments than using FLbutton built-in mechanism
instr 1
; trigger when button value goes from off to on
kOnTrig trigger gkRecord,0.5,0
; start instrument with a held note when trigger received
schedkwhen kOnTrig,0,0,2,0,-1
; trigger when button value goes from off to on
kOnTrig trigger gkPlay,0.5,0
; start instrument with a held note when trigger received
schedkwhen kOnTrig,0,0,3,0,-1
endin
instr 2 ; Record gesture
if gkRecord==0 then ; If record button is deactivated...
turnoff ; ...turn this instrument off.
endif
; call UDO
RecordController gkval,gidata
; Generate a sound.
kporttime linseg 0,0.001,0.02
kval portk gkval,kporttime
asig poscil 0.2,cpsoct((kval*2)+7)
out asig
endin
instr 3 ; Playback recorded gesture
if gkPlay==0 then ; if play button is deactivated...
turnoff ; ...turn this instrument off.
endif
kval PlaybackController gidata
; send initial value to controller
FLsetVal_i i(kval),gihval
; Send values to slider when needed.
FLsetVal changed(kval),kval,gihval
; Generate a sound.
kporttime linseg 0,0.001,0.02
kval portk gkval,kporttime
asig poscil 0.2,cpsoct((kval*2)+7)
out asig
; stop note when end of table reached
kTime timeinsts ; time in seconds since this note began
; read complete gesture duration from index zero
iRecTime tablei 0,gidata
; if we have reach complete duration of gesture...
if kTime>=iRecTime then
; deactivate play button (which will in turn, turn off this note.)
FLsetVal 1,0,gihPlay
endif
endin
instr 4 ; save table
ftsave "ControllerData.txt", 0, gidata
endin
instr 5 ; load table
ftload "ControllerData.txt", 0, gidata
endin
</CsInstruments>
<CsScore>
i 1 0 3600
</CsScore>
</CsoundSynthesizer>
READING MIDI FILES
Instead of using either the standard Csound score or live midi events as input for a orchestra Csound can read a midi file and use the data contained within it as if it were a live midi input.
The command line flag to instigate reading from a midi file is '-F' followed by the name of the file or the complete path to the file if it is not in the same directory as the .csd file. Midi channels will be mapped to instrument according to the rules and options discussed in Triggering Instrument Instances and all controllers can be interpretted as desired using the techniques discussed in Working with Controllers. One thing we need to be concerned with is that without any events in our standard Csound score our performance will terminate immedately. To circumvent this problem we need some sort of dummy event in our score to fool Csound into keeping going until our midi file has completed. Something like the following, placed in the score, is often used.
f 0 3600
This dummy 'f' event will force Csound to wait for 3600 second (1 hour) before terminating performance. It doesn't really matter what number of seconds we put in here, as long as it is more than the number of seconds duration of the midi file. Alternatively a conventional 'i' score event can also keep performance going; sometimes we will have, for example, a reverb effect running throughout the performance which can also prevent Csound from terminating. Performance can be interrupted at any time by typing ctrl+c in the terminal window.
The following example plays back a midi file using Csound's 'fluidsynth' family of opcodes to facilitate playing soundfonts (sample libraries). For more information on these opcodes please consult the Csound Reference Manual. In order to run the example you will need to download a midi file and two (ideally contrasting) soundfonts. Adjust the references to these files in the example accordingly. Free midi files and soundfonts are readily available on the internet. I am suggesting that you use contrasting soundfonts, such as a marimba and a trumpet, so that you can easily hear the parsing of midi channels in the midi file to different Csound instruments. In the example channels 1,3,5,7,9,11,13 and 15 play back using soundfont 1 and channels 2,4,6,8,10,12,14 and 16 play back using soundfont 2. When using fluidsynth in Csound we normally use an 'always on' instrument to gather all the audio from the various soundfonts (in this example instrument 99) which also conveniently keeps performance going while our midi file plays back.
EXAMPLE 07D01_ReadMidiFile.csd
<CsoundSynthesizer>
<CsOptions>
;'-F' flag reads in a midi file
-F AnyMIDIfile.mid
</CsOptions>
<CsInstruments>
;Example by Iain McCurdy
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
sr = 44100
ksmps = 32
nchnls = 2
giEngine fluidEngine; start fluidsynth engine
; load a soundfont
iSfNum1 fluidLoad "ASoundfont.sf2", giEngine, 1
; load a different soundfont
iSfNum2 fluidLoad "ADifferentSoundfont.sf2", giEngine, 1
; direct each midi channels to a particular soundfonts
fluidProgramSelect giEngine, 1, iSfNum1, 0, 0
fluidProgramSelect giEngine, 3, iSfNum1, 0, 0
fluidProgramSelect giEngine, 5, iSfNum1, 0, 0
fluidProgramSelect giEngine, 7, iSfNum1, 0, 0
fluidProgramSelect giEngine, 9, iSfNum1, 0, 0
fluidProgramSelect giEngine, 11, iSfNum1, 0, 0
fluidProgramSelect giEngine, 13, iSfNum1, 0, 0
fluidProgramSelect giEngine, 15, iSfNum1, 0, 0
fluidProgramSelect giEngine, 2, iSfNum2, 0, 0
fluidProgramSelect giEngine, 4, iSfNum2, 0, 0
fluidProgramSelect giEngine, 6, iSfNum2, 0, 0
fluidProgramSelect giEngine, 8, iSfNum2, 0, 0
fluidProgramSelect giEngine, 10, iSfNum2, 0, 0
fluidProgramSelect giEngine, 12, iSfNum2, 0, 0
fluidProgramSelect giEngine, 14, iSfNum2, 0, 0
fluidProgramSelect giEngine, 16, iSfNum2, 0, 0
instr 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 ; fluid synths for channels 1-16
iKey notnum ; read in midi note number
iVel ampmidi 127 ; read in key velocity
; create a note played by the soundfont for this instrument
fluidNote giEngine, p1, iKey, iVel
endin
instr 99 ; gathering of fluidsynth audio and audio output
aSigL, aSigR fluidOut giEngine ; read all audio from soundfont
outs aSigL, aSigR ; send audio to outputs
endin
</CsInstruments>
<CsScore>
i 99 0 3600 ; audio output instrument also keeps performance going
e
</CsScore>
<CsoundSynthesizer>
Midi file input can be combined with other Csound inputs from the score or from live midi and also bear in mind that a midi file doesn't need to contain midi note events, it could instead contain, for example, a sequence of controller data used to automate parameters of effects during a live performance.
Rather than to directly play back a midi file using Csound instruments it might be useful to import midi note events as a standard Csound score. This way events could be edited within the Csound editor or several scores could be combined. The following example takes a midi file as input and outputs standard Csound .sco files of the events contained therein. For convenience each midi channel is output to a separate .sco file, therefore up to 16 .sco files will be created. Multiple .sco files can be later recombined by using #include... statements or simply by using copy and paste.
The only tricky aspect of this example is that note-ons followed by note-offs need to be sensed and calculated as p3 duration values. This is implemented by sensing the note-off by using the release opcode and at that moment triggering a note in another instrument with the required score data. It is this second instrument that is responsible for writing this data to a score file. Midi channels are rendered as p1 values, midi note numbers as p4 and velocity values as p5.
EXAMPLE 07D02_MidiToScore.csd
<CsoundSynthesizer>
<CsOptions>
; enter name of input midi file
-F InputMidiFile.mid
</CsOptions>
<CsInstruments>
; Example by Iain McCurdy
;ksmps needs to be 10 to ensure accurate rendering of timings
ksmps = 10
massign 0,1
instr 1
iChan midichn
iCps cpsmidi ; read pitch in frequency from midi notes
iVel veloc 0, 127 ; read in velocity from midi notes
kDur timeinsts ; running total of duration of this note
kRelease release ; sense when note is ending
if kRelease=1 then ; if note is about to end
; p1 p2 p3 p4 p5 p6
event "i", 2, 0, kDur, iChan, iCps, iVel ; send full note data to instr 2
endif
endin
instr 2
iDur = p3
iChan = p4
iCps = p5
iVel = p6
iStartTime times ; read current time since the start of performance
; form file name for this channel (1-16) as a string variable
SFileName sprintf "Channel%d.sco",iChan
; write a line to the score for this channel's .sco file
fprints SFileName, "i%d\\t%f\\t%f\\t%f\\t%d\\n",\
iChan,iStartTime-iDur,iDur,iCps,iVel
endin
</CsInstruments>
<CsScore>
f 0 480 ; ensure this duration is as long or longer that duration of midi file
e
</CsScore>
</CsoundSynthesizer>
The example above ignores continuous controller data, pitch bend and aftertouch. The second example on the page in the Csound Manual for the opcode fprintks renders all midi data to a score file.
MIDI OUTPUT
Csound's ability to output midi data in real-time can open up many possibilities. We can relay the Csound score to a hardware synthesizer so that it plays the notes in our score, instead of a Csound instrument. We can algorithmically generate streams of notes within the orchestra and have these played by the external device. We could even route midi data internally to another piece of software. Csound could be used as a device to transform incoming midi data, transforming, transposing or arpeggiating incoming notes before they are output again. Midi output could also be used to preset faders on a motorized fader box to desired initial locations.
Initiating Realtime MIDI Output
The command line flag for realtime midi output is -Q. Just as when setting up an audio input or output device or a midi input device we must define the desired device number after the flag. When in doubt what midi output devices we have on our system we can always specify an 'out of range' device number (e.g. -Q999) in which case Csound will not run but will instead give an error and provide us with a list of available devices and their corresponding numbers. We can then insert an appropriate device number.
midiout - Outputting Raw MIDI Data
The analog of the opcode for the input of raw midi data, midiin, is midiout. midiout will output a midi message with its given input arguments once every k period - this could very quickly lead to clogging of incoming midi data in the device to which midi is begin sent unless measures are taken to restrain its output. In the following example this is dealt with by turning off the instrument as soon as the midiout line has been executed just once by using the turnoff opcode. Alternative approaches would be to set the status byte to zero after the first k pass or to embed the midiout within a conditional (if... then...) so that its rate of execution can be controlled in some way.
Another thing we need to be aware of is that midi notes do not contain any information about note duration; instead the device playing the note waits until it receives a corresponding note-off instruction on the same midi channel and with the same note number before stopping the note. We must be mindful of this when working with midiout. The status byte for a midi note-off is 128 but it is more common for note-offs to be expressed as a note-on (status byte 144) with zero velocity. In the following example two notes (and corresponding note offs) are send to the midi output - the first note-off makes use of the zero velocity convention whereas the second makes use of the note-off status byte. Hardware and software synths should respond similarly to both. One advantage of the note-off message using status byte 128 is that we can also send a note-off velocity, i.e. how forcefully we release the key. Only more expensive midi keyboards actually sense and send note-off velocity and it is even rarer for hardware to respond to received note-off velocities in a meaningful way. Using Csound as a sound engine we could respond to this data in a creative way however.
In order for the following example to work you must connect a midi sound module or keyboard receiving on channel 1 to the midi output of your computer. You will also need to set the appropriate device number after the '-Q' flag.
No use is made of audio so sample rate (sr), and number of channels (nchnls) are left undefined - nonetheless they will assume default values.
EXAMPLE 07E01_midiout.csd
<CsoundSynthesizer>
<CsOptions>
; amend device number accordingly
-Q999
</CsOptions>
<CsInstruments>
ksmps = 32 ;no audio so sr and nchnls irrelevant
instr 1
; arguments for midiout are read from p-fields
istatus init p4
ichan init p5
idata1 init p6
idata2 init p7
midiout istatus, ichan, idata1, idata2; send raw midi data
turnoff ; turn instrument off to prevent reiterations of midiout
endin
</CsInstruments>
<CsScore>
;p1 p2 p3 p4 p5 p6 p7
i 1 0 0.01 144 1 60 100 ; note on
i 1 2 0.01 144 1 60 0 ; note off (using velocity zero)
i 1 3 0.01 144 1 60 100 ; note on
i 1 5 0.01 128 1 60 100 ; note off (using 'note off' status byte)
</CsScore>
</CsoundSynthesizer>
The use of separate score events for note-ons and note-offs is rather cumbersome. It would be more sensible to use the Csound note duration (p3) to define when the midi note-off is sent. The next example does this by utilising a release flag generated by the release opcode whenever a note ends and sending the note-off then.
EXAMPLE 07E02_score_to_midiout.csd
<CsoundSynthesizer> <CsOptions> ; amend device number accordingly -Q999 </CsOptions> <CsInstruments> ksmps = 32 ;no audio so sr and nchnls omitted instr 1 ;arguments for midiout are read from p-fields istatus init p4 ichan init p5 idata1 init p6 idata2 init p7 kskip init 0 if kskip=0 then midiout istatus, ichan, idata1, idata2; send raw midi data (note on) kskip = 1; ensure that the note on will only be executed once endif krelease release; normally output is zero, on final k pass output is 1 if krelease=1 then; i.e. if we are on the final k pass... midiout istatus, ichan, idata1, 0; send raw midi data (note off) endif endin </CsInstruments> <CsScore> ;p1 p2 p3 p4 p5 p6 p7 i 1 0 4 144 1 60 100 i 1 1 3 144 1 64 100 i 1 2 2 144 1 67 100 f 0 5; extending performance time prevents note-offs from being lost </CsScore> </CsoundSynthesizer>
Obviously midiout is not limited to only sending only midi note information but instead this information could include continuous controller information, pitch bend, system exclusive data and so on. The next example, as well as playing a note, sends controller 1 (modulation) data which rises from zero to maximum (127) across the duration of the note. To ensure that unnessessary midi data is not sent out, the output of the line function is first converted into integers, and midiout for the continuous controller data is only executed whenever this integer value changes. The function that creates this stream of data goes slightly above this maximum value (it finishes at a value of 127.1) to ensure that a rounded value of 127 is actually achieved.
In practice it may be necessary to start sending the continuous controller data slightly before the note-on to allow the hardware time to respond.
EXAMPLE 07E03_midiout_cc.csd
<CsoundSynthesizer>
<CsOptions>
; amend device number accordingly
-Q999
</CsOptions>
<CsInstruments>
ksmps = 32 ; no audio so sr and nchnls irrelevant
instr 1
; play a midi note
; read in values from p-fields
ichan init p4
inote init p5
iveloc init p6
kskip init 0 ; 'skip' flag ensures that note-on is executed just once
if kskip=0 then
midiout 144, ichan, inote, iveloc; send raw midi data (note on)
kskip = 1 ; flip flag to prevent repeating the above line
endif
krelease release ; normally zero, on final k pass this will output 1
if krelease=1 then ; if we are on the final k pass...
midiout 144, ichan, inote, 0 ; send a note off
endif
; send continuous controller data
iCCnum = p7
kCCval line 0, p3, 127.1 ; continuous controller data function
kCCval = int(kCCval) ; convert data function to integers
ktrig changed kCCval ; generate a trigger each time kCCval changes
if ktrig=1 then ; if kCCval has changed...
midiout 176, ichan, iCCnum, kCCval ; ...send a controller message
endif
endin
</CsInstruments>
<CsScore>
;p1 p2 p3 p4 p5 p6 p7
i 1 0 5 1 60 100 1
f 0 7 ; extending performance time prevents note-offs from being lost
</CsScore>
</CsoundSynthesizer>
midion - Outputting MIDI Notes Made Easier
midiout is the most powerful opcode for midi output but if we are only interested in sending out midi notes from an instrument then the midion opcode simplifies the procedure as the following example demonstrates by playing a simple major arpeggio.
EXAMPLE 07E04_midion.csd
<CsoundSynthesizer>
<CsOptions>
; amend device number accordingly
-Q999
</CsOptions>
<CsInstruments>
; Example by Iain McCurdy
ksmps = 32 ;no audio so sr and nchnls irrelevant
instr 1
; read values in from p-fields
kchn = p4
knum = p5
kvel = p6
midion kchn, knum, kvel ; send a midi note
endin
</CsInstruments>
<CsScore>
;p1 p2 p3 p4 p5 p6
i 1 0 2.5 1 60 100
i 1 0.5 2 1 64 100
i 1 1 1.5 1 67 100
i 1 1.5 1 1 72 100
f 0 30 ; extending performance time prevents note-offs from being missed
</CsScore>
</CsoundSynthesizer>
Changing any of midion's k-rate input arguments in realtime will force it to stop the current midi note and send out a new one with the new parameters.
midion2 allows us to control when new notes are sent (and the current note is stopped) through the use of a trigger input. The next example uses 'midion2' to algorithmically generate a melodic line. New note generation is controlled by a metro, the rate of which undulates slowly through the use of a randomi function.
EXAMPLE 07E05_midion2.csd
<CsoundSynthesizer>
<CsOptions>
; amend device number accordingly
-Q999
</CsOptions>
<CsInstruments>
; Example by Iain McCurdy
ksmps = 32 ; no audio so sr and nchnls irrelevant
instr 1
; read values in from p-fields
kchn = p4
knum random 48,72.99 ; note numbers chosen randomly across a 2 octaves
kvel random 40, 115 ; velocities are chosen randomly
krate randomi 1,2,1 ; rate at which new notes will be output
ktrig metro krate^2 ; 'new note' trigger
midion2 kchn, int(knum), int(kvel), ktrig ; send midi note if ktrig=1
endin
</CsInstruments>
<CsScore>
i 1 0 20 1
f 0 21 ; extending performance time prevents the final note-off being lost
</CsScore>
</CsoundSynthesizer>
'midion' and 'midion2' generate monophonic melody lines with no gaps between notes.
moscil works in a slightly different way and allows us to explicitly define note durations as well as the pauses between notes thereby permitting the generation of more staccato melodic lines. Like 'midion' and 'midion2', 'moscil' will not generate overlapping notes (unless two or more instances of it are concurrent). The next example algorithmically generates a melodic line using 'moscil'.
EXAMPLE 07E06_moscil.csd
<CsoundSynthesizer>
<CsOptions>
; amend device number accordingly
-Q999
</CsOptions>
<CsInstruments>
; Example by Iain McCurdy
ksmps = 32 ;no audio so sr and nchnls omitted
seed 0; random number generators seeded by system clock
instr 1
; read value in from p-field
kchn = p4
knum random 48,72.99 ; note numbers chosen randomly across a 2 octaves
kvel random 40, 115 ; velocities are chosen randomly
kdur random 0.2, 1 ; note durations chosen randomly from 0.2 to 1
kpause random 0, 0.4 ; pauses betw. notes chosen randomly from 0 to 0.4
moscil kchn, knum, kvel, kdur, kpause ; send a stream of midi notes
endin
</CsInstruments>
<CsScore>
;p1 p2 p3 p4
i 1 0 20 1
f 0 21 ; extending performance time prevents final note-off from being lost
</CsScore>
</CsoundSynthesizer>
MIDI File Output
As well as (or instead of) outputting midi in realtime, Csound can render data from all of its midi output opcodes to a midi file. To do this we use the '--midioutfile=' flag followed by the desired name for our file. For example:
<CsOptions> -Q2 --midioutfile=midiout.mid </CsOptions>
will simultaneously stream realtime midi to midi output device number 2 and render to a file named 'midiout.mid' which will be saved in our home directory.
08 OTHER COMMUNICATION
OPEN SOUND CONTROL - NETWORK COMMUNICATION
Open Sound Control (OSC) is a network protocol format for musical control data communication. A few of its advantages compared to MIDI are, that it's more accurate, quicker and much more flexible. With OSC you can easily send messages to other software independent if it's running on the same machine or over network. There is OSC support in software like PD, Max/MSP, Chuck or SuperCollider. A nice screencast of Andrés Cabrera shows communication between PD and Csound via OSC.1
OSC messages contain an IP adress with port information and the data-package, which will be send over network. In Csound, there are two opcodes, which provide access to network communication called OSCsend and OSClisten.
Example 08A01_osc.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 48000
ksmps = 32
nchnls = 2
0dbfs = 1
; localhost means communication on the same machine, otherwise you need
; an IP adress
#define IPADDRESS # "localhost" #
#define S_PORT # 47120 #
#define R_PORT # 47120 #
turnon 1000 ; starts instrument 1000 immediately
turnon 1001 ; starts instrument 1001 immediately
instr 1000 ; this instrument sends OSC-values
kValue1 randomh 0, 0.8, 4
kNum randomh 0, 8, 8
kMidiKey tab (int(kNum)), 2
kOctave randomh 0, 7, 4
kValue2 = cpsmidinn (kMidiKey*kOctave+33)
kValue3 randomh 0.4, 1, 4
Stext sprintf "%i", $S_PORT
OSCsend kValue1+kValue2, $IPADDRESS, $S_PORT, "/QuteCsound",
"fff", kValue1, kValue2, kValue3
endin
instr 1001 ; this instrument receives OSC-values
kValue1Received init 0.0
kValue2Received init 0.0
kValue3Received init 0.0
Stext sprintf "%i", $R_PORT
ihandle OSCinit $R_PORT
kAction OSClisten ihandle, "/QuteCsound", "fff",
kValue1Received, kValue2Received, kValue3Received
if (kAction == 1) then
printk2 kValue2Received
printk2 kValue1Received
endif
aSine poscil3 kValue1Received, kValue2Received, 1
; a bit reverbration
aInVerb = aSine*kValue3Received
aWetL, aWetR freeverb aInVerb, aInVerb, 0.4, 0.8
outs aWetL+aSine, aWetR+aSine
endin
</CsInstruments>
<CsScore>
f 1 0 1024 10 1
f 2 0 8 -2 0 2 4 7 9 11 0 2
e 3600
</CsScore>
</CsoundSynthesizer>
; example by Alex Hofmann (Mar. 2011)
- As another example you can communicate via OSC between Csound and Grame's Inscore. Find the code at https://github.com/joachimheintz/cs_inscore and video tutorials at
http://vimeo.com/54160283 (installation)
http://vimeo.com/54160405 (examples) ^
CSOUND AND ARDUINO
It is the intention of this chapter to suggest a number of ways in which Csound can be paired with an Arduino prototyping circuit board. It is not the intention of this chapter to go into any detail about how to use an Arduino, there is already a wealth of information available elsewhere online about this. It is common to use an Arduino and Csound with another program functioning as an interpreter, so therefore some time is spent discussing these other programs.
An Arduino is a simple microcontroller circuit board that has become enormously popular as a component in multidisciplinary and interactive projects for musicians and artists since its introduction in 2005. An Arduino board can be programmed to do many things and to send and receive data to and from a wide variety of other components and devices. As such it is impossible to specifically define its function here. An Arduino is normally programmed using its own development environment (IDE). A program is written on a computer which is then uploaded to the Arduino; the Arduino then runs this program, independent of the computer if necessary. Arduino's IDE is based on that used by Processing and Wiring. Arduino programs are often referred to as "sketches". There now exists a plethora of Arduino variants and even a number of derivatives and clones but all function in more or less the same way.
Interaction between an Arduino and Csound is essentially a question of communication and as such a number of possible solutions exist. This chapter will suggest several possibilities and it will then be up to the user to choose the one most suitable for their requirements. Most Arduino boards communicate using serial communication (normally via a USB cable). A number of Arduino programs, called "Firmata", exist that are intended to simplify and standardise communication between Arduinos and software. Through the use of a Firmata the complexity of Arduino's serial communication is shielded from the user and a number of simpler objects, ugens or opcodes (depending on what the secondary software is) can instead be used to establish communication. Unfortunately Csound is rather poorly served with facilities to communicate using the Firmata (although this will hopefully improve in the future) so it might prove easiest to use another program (such as Pd or Processing) as an intermediary between the Arduino and Csound.
Arduino - Pd - Csound
First we will consider communication between an Arduino (running a Standard Firmata) and Pd. Later we can consider the options for further communication from Pd to Csound.
Assuming that the Arduino IDE (integrated development environment) has been installed and that the Arduino has been connected, we should then open and upload a Firmata sketch. One can normally be found by going to File -> Examples -> Firmata -> ... There will be a variety of flavours from which to choose but "StandardFirmata" should be a good place to start. Choose the appropriate Arduino board type under Tools -> Board -> ... and then choose the relevant serial port under Tools -> Serial Port -> ... Choosing the appropriate serial port may require some trial and error but if you have chosen the wrong one this will become apparent when you attempt to upload the sketch. Once you have established the correct serial port to use, it is worth taking a note of which number on the list (counting from zero) this corresponds to as this number will be used by Pd to communicate with the Arduino. Finally upload the sketch by clicking on the right-pointing arrow button.
Assuming that Pd is already installed, it will also be necessary to install an add-on library for Pd called Pduino. Follow its included instructions about where to place this library on your platform and then reopen Pd. You will now have access to a set of Pd objects for communicating with your Arduino. The Pduino download will also have included a number of examples Pd. "arduino-test.pd" will probably be the best patch to start. First set the appropriate serial port number to establish communication and then set Arduino pins as "input", "output" etc. as you desire. It is beyond the scope of this chapter to go into further detail regarding setting up an Arduino with sensors and auxiliary components, suffice to say that communication to an Arduino is normally tested by 'blinking' digital pin 13 and communication from an Arduino is normally tested by connecting a 10 kilo-ohm (10k) potentiometer to analog pin zero. For the sake of argument, we shall assume in this tutorial that we are setting the Arduino as a hardware controller and have a potentiometer connected to pin 0.

This picture below demonstrates a simple Pd patch that uses Pduino's objects to receive communication from Arduino's analog and digital inputs. (Note that digital pins 0 and 1 are normally reserved for serial communication if the USB serial communication is unavailable.) In this example serial port '5' has been chosen. Once the analogIns enable box for pin 0 is checked, moving the potentiometer will change the values in the left-most number box (and move the slider connected to it). Arduino's analog inputs generate integers with 10-bit resolution (0 - 1023) but these values will often be rescaled as floats within the range 0 - 1 in the host program for convenience.
Having established communication between the Arduino and Pd we can now consider the options available to us for communicating between Pd and Csound. The most obvious (but not necessarily the best or most flexible) method is to use Pd's csoundapi~ object (csound6~ in Csound6). The above example could be modified to employ csoundapi~ as shown below.
The outputs from the first two Arduino analog controls are passed into Csound using its API. Note that we should use the unpegged (not quantised in time) values directly from the 'route' object. The Csound .csd file 'control.csd' is called upon by Pd and it should reside in the same directory as the Pd patch. Establishing communication to and from Pd could employ code such as that shown below. Data from controller one (Arduino analog 0) is used to modulate the amplitude of an oscillator and data from controller two (Arduino analog 1) varies its pitch across a four octave range.
EXAMPLE 08B01_Pd_to_Csound.csd
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
sr = 44100
nchnls = 2
0dbfs = 1
ksmps = 32
instr 1
; read in controller data from Pd via the API using 'invalue'
kctrl1 invalue "ctrl1"
kctrl2 invalue "ctrl2"
; re-range controller values from 0 - 1 to 7 - 11
koct = (kctrl2*4)+7
; create an oscillator
a1 vco2 kctrl1,cpsoct(koct),4,0.1
outs a1,a1
endin
</CsInstruments>
<CsScore>
i 1 0 10000
e
</CsScore>
</CsoundSynthesizer>
Communication from Pd into Csound is established using the invalue opcodes and audio is passed back to Pd from Csound using outs. Note that Csound does not address the computer's audio hardware itself but merely passes audio signals back to Pd. Greater detail about using Csound within Pd can be found in the chapter Csound in Pd.
A disadvantage of using the method is that in order to modify the Csound patch it will require being edited in an external editor, re-saved, and then the Pd patch will need to be reloaded to reflect these changes. This workflow might be considered rather inefficient.
Another method of data communication between PD and Csound could be to use MIDI. In this case some sort of MIDI connection node or virtual patchbay will need to be employed. On Mac this could be the IAC driver, on Windows this could be MIDI Yoke and on Linux this could be Jack. This method will have the disadvantage that the Arduino's signal might have to be quantised in order to match the 7-bit MIDI controller format but the advantage is that Csound's audio engine will be used (not Pd's; in fact audio can be disabled in Pd) so that making modifications to the Csound .csd and hearing the changes should require fewer steps.
A final method for communication between Pd and Csound is to use OSC. This method would have the advantage that analog 10 bit signal would not have to be quantised. Again workflow should be good with this method as Pd's interaction will effectively be transparent to the user and once started it can reside in the background during working. Communication using OSC is also used between Processing and Csound so is described in greater detail below.
Arduino - Processing - Csound
It is easy to communicate with an Arduino using a Processing sketch and any data within Processing can be passed to Csound using OSC.
The following method makes use of the Arduino and P5 (glove) libraries for processing. Again these need to be copied into the appropriate directory for your chosen platform in order for Processing to be able to use them. Once again there is no requirement to actually know very much about Processing beyond installing it and running a patch (sketch). The following sketch will read all Arduino inputs and output them as OSC.
Start the Processing sketch by simply clicking the triangle button at the top-left of the GUI. Processing is now reading serial data from the Arduino and transmitting this as OSC data within the computer.
The OSC data sent by Processing can be read by Csound using its own OSC opcodes. The following example simply reads in data transmitted by Arduino's analog pin 0 and prints changed values to the terminal. To read in data from all analog and digital inputs you can use this example .csd.
EXAMPLE 08B02_Processing_to_Csound.csd
<CsoundSynthesizer>
<CsOptions>
-o dac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 8
nchnls = 1
0dbfs = 1
; handle used to reference osc stream
gihandle OSCinit 12001
instr 1
; initialise variable used for analog values
gkana0 init 0
; read in OSC channel '/analog/0'
gktrigana0 OSClisten gihandle, "/analog/0", "i", gkana0
; print changed values to terminal
printk2 gkana0
endin
</CsInstruments>
<CsScore>
i 1 0 3600
e
</CsScore>
</CsoundSynthesizer>
Also worth in investigating is Jacob Joaquin's Csoundo - a Csound library for Processing. This library will allow closer interaction between Processing and Csound in the manner of the csoundapi~ object in Pd. This project has more recently been developed by Rory Walsh.
Arduino as a MIDI Device
Some users might find it most useful to simply set the Arduino up as a MIDI device and to use that protocol for communication. In order to do this all that is required is to connect MIDI pin 4 to the Arduino's 5v via a 200k resistor, to connect MIDI pin 5 to the Arduino's TX (serial transmit) pin/pin 1 and to connect MIDI pin 2 to ground, as shown below. In order to program the Arduino it will be necessary to install Arduino's MIDI library.

Programming an Arduino to generate a MIDI controller signal from analog pin 0 could be done using the following code:
// example written by Iain McCurdy
// import midi library
#include <MIDI.h>
const int analogInPin = A0; // choose analog input pin
int sensorValue = 0; // sensor value variable
int oldSensorValue = 0; // sensor value from previous pass
int midiChannel = 1; // set MIDI channel
void setup()
{
MIDI.begin(1);
}
void loop()
{
sensorValue = analogRead(analogInPin);
// only send out a MIDI message if controller has changed
if (sensorValue!=oldSensorValue)
{
// controller 1, rescale value from 0-1023 (Arduino) to 0-127 (MIDI)
MIDI.sendControlChange(1,sensorValue/8,midiChannel);
oldSensorValue = sensorValue; // set old sensor value to current
}
}
delay(10);
}
Data from the Arduino can now be read using Csound's ctrl7 opcodes for reading MIDI controller data.
The Serial Opcodes
Serial data can also be read directly from the Arduino by Csound by using Matt Ingalls' opcodes for serial communication: serialBegin and serialRead.
An example Arduino sketch for serial communication could be as simple as this:
// Example written by Matt Ingalls
// ARDUINO CODE:
void setup() {
// enable serial communication
Serial.begin(9600);
// declare pin 9 to be an output:
pinMode(9, OUTPUT);
}
void loop()
{
// only do something if we received something (this should be at csound's k-rate)
if (Serial.available())
{
// set the brightness of LED (connected to pin 9) to our input value
int brightness = Serial.read();
analogWrite(9, brightness);
// while we are here, get our knob value and send it to csound
int sensorValue = analogRead(A0);
Serial.write(sensorValue/4); // scale to 1-byte range (0-255)
}
}
It will be necessary to provide the correct address of the serial port to which the Arduino is connected (in the given example the Windows platform was being used and the port address was /COM4).
It will be necessary to scale the value to correspond to the range provided by a single byte (0-255) so therefore the Arduino's 10 bit analog input range (0-1023) will have to be divided by four.
EXAMPLE 08B03_Serial_Read.csd
; Example written by Matt Ingalls ; CSOUND CODE: ; run with a commandline something like: ; csound --opcode-lib=serialOpcodes.dylib serialdemo.csd -odac -iadc <CsoundSynthesizer> <CsOptions> </CsOptions> ;--opcode-lib=serialOpcodes.dylib -odac <CsInstruments> ksmps = 500 ; the default krate can be too fast for the arduino to handle 0dbfs = 1 instr 1 iPort serialBegin "/COM4", 9600 kVal serialRead iPort printk2 kVal endin </CsInstruments> <CsScore> i 1 0 3600 e </CsScore> </CsoundSynthesizer>
This example will read serial data from the Arduino and print it to the terminal. Reading output streams from several of Arduino's sensor inputs simultaneously will require more complex parsing of data within Csound as well as more complex packaging of data from the Arduino. This is demonstrated in the following example which also shows how to handle serial transmission of integers larger than 255 (the Arduino analog inputs have 10 bit resolution).
First the Arduino sketch, in this case reading and transmitting two analog and one digital input:
// Example written by Sigurd Saue
// ARDUINO CODE:
// Analog pins
int potPin = 0;
int lightPin = 1;
// Digital pin
int buttonPin = 2;
// Value IDs (must be between 128 and 255)
byte potID = 128;
byte lightID = 129;
byte buttonID = 130;
// Value to toggle between inputs
int select;
/*
** Two functions that handles serial send of numbers of varying length
*/
// Recursive function that sends the bytes in the right order
void serial_send_recursive(int number, int bytePart)
{
if (number < 128) { // End of recursion
Serial.write(bytePart); // Send the number of bytes first
}
else {
serial_send_recursive((number >> 7), (bytePart + 1));
}
Serial.write(number % 128); // Sends one byte
}
void serial_send(byte id, int number)
{
Serial.write(id);
serial_send_recursive(number, 1);
}
void setup() {
// enable serial communication
Serial.begin(9600);
pinMode(buttonPin, INPUT);
}
void loop()
{
// Only do something if we received something (at csound's k-rate)
if (Serial.available())
{
// Read the value (to empty the buffer)
int csound_val = Serial.read();
// Read one value at the time (determined by the select variable)
switch (select) {
case 0: {
int potVal = analogRead(potPin);
serial_send(potID, potVal);
}
break;
case 1: {
int lightVal = analogRead(lightPin);
serial_send(lightID, lightVal);
}
break;
case 2: {
int buttonVal = digitalRead(buttonPin);
serial_send(buttonID, buttonVal);
}
break;
}
// Update the select (0, 1 and 2)
select = (select+1)%3;
}
}
The solution is similar to MIDI messages. You have to define an ID (a unique number >= 128) for every sensor. The ID behaves as a status byte that clearly marks the beginning of a message received by Csound. The remaining bytes of the message will all have a most significant bit equal to zero (value < 128). The sensor values are transmitted as ID, length (number of data bytes), and the data itself. The recursive function serial_send_recursive counts the number of data bytes necessary and sends the bytes in the correct order. Only one sensor value is transmitted for each run through the Arduino loop.
The Csound code receives the values with the ID first. Of course you have to make sure that the IDs in the Csound code matches the ones in the Arduino sketch. Here's an example of a Csound orchestra that handles the messages sent from the Arduino sketch:
EXAMPLE 08B04_Serial_Read_multiple.csd
; Example written by Sigurd Saue ; CSOUND CODE: <CsoundSynthesizer> <CsOptions> -d -odac </CsOptions> <CsInstruments> sr = 44100 ksmps = 500 ; the default krate can be too fast for the arduino to handle nchnls = 2 0dbfs = 1 giSaw ftgen 0, 0, 4096, 10, 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8 instr 1 ; Initialize the three variables to read kPot init 0 kLight init 0 kButton init 0 iPort serialBegin "/COM5", 9600 ;connect to the arduino with baudrate = 9600 serialWrite iPort, 1 ;Triggering the Arduino (k-rate) kValue = 0 kType serialRead iPort ; Read type of data (pot, light, button) if (kType >= 128) then kIndex = 0 kSize serialRead iPort loopStart: kValue = kValue << 7 kByte serialRead iPort kValue = kValue + kByte loop_lt kIndex, 1, kSize, loopStart endif if (kValue < 0) kgoto continue if (kType == 128) then ; This is the potmeter kPot = kValue elseif (kType == 129) then ; This is the light kLight = kValue elseif (kType == 130) then ; This is the button (on/off) kButton = kValue endif continue: ; Here you can do something with the variables kPot, kLight and kButton ; printks "Pot %f\n", 1, kPot ; printks "Light %f\n", 1, kLight ; printks "Button %d\n", 1, kButton ; Example: A simple oscillater controlled by the three parameters kAmp port kPot/1024, 0.1 kFreq port (kLight > 100 ? kLight : 100), 0.1 aOut oscil kAmp, kFreq, giSaw if (kButton == 0) then out aOut endif endin </CsInstruments> <CsScore> i 1 0 60 ; Duration one minute e </CsScore> </CsoundSynthesizer>
Remember to provide the correct address of the serial port to which the Arduino is connected (the example uses "/COM5").
HID
Another option for communication has been made available by a new Arduino board called "Leonardo". It pairs with a computer as if it were an HID (Human Interface Device) such as a mouse, keyboard or a gamepad. Sensor data can therefore be used to imitate the actions of a mouse connected to the computer or keystrokes on a keyboard. Csound is already equipped with opcodes to make use of this data. Gamepad-like data is perhaps the most useful option though and there exist opcodes (at least in the Linux version) for reading gamepad data. It is also possible to read in data from a gamepad using pygame and Csound's python opcodes.
09 CSOUND IN OTHER APPLICATIONS
CSOUND IN PD
INSTALLING
You can embed Csound in PD via the external object csound6~1 which has been written by Victor Lazzarini. This external is either part of the Csound distribution or can be built from the sources at https://github.com/csound/csound_pd . In the examples folder of this repository you can also find all the .csd and .pd files of this chapter.
On Ubuntu Linux, you can install the csound6~ via the Synaptic Package Manager. Just look for "csound6~" or "pd-csound", check "install", and your system will install the library at the appropriate location. If you build Csound from sources, go to https://github.com/csound/csound_pd and follow the build instructions. Once it is compiled, the object will appear as csound6~.pd_linux and should be copied (together with csound6~-help.pd) to /usr/lib/pd/extra, so that PD can find it. If not, add it to PD's search path (File->Path...).
On Mac OSX, you find the csound6~ external, help file and examples in https://github.com/csound/csound_pd/releases
(Prior to 6.11, it was in /Library/Frameworks/CsoundLib64.framework/Versions/6.0/Resources/PD.)
Put these files in a folder which is in PD's search path. For PD-extended, it is by default ~/Library/Pd. But you can put it anywhere. Just make sure that the location is specified in PD's Preferences > Path... menu.
On Windows, you find the csound6~ external, help file and examples in https://github.com/csound/csound_pd/releases
For older versions of Csound, the csound6~ object was included in the installer. The description is left here for the case that someone needs to install one of these older versions:
<<while installing Csound, open up the "Front ends" component in the Installer box and make sure the item "csound6~" is checked:
After having finished the installation, you will find csound6~.dll in the csound/bin folder. Copy this file into the pd/extra folder, or in any other location in PD's search path. Due to the dependencies in Csound 6, you may find that it works better to add the Csound/bin directory to the search paths in Pd's Preferences window.
Note for Csound 6.07 for Windows: As it is build for 64bit architecture, but PD does not fully support the 64 bit CPU architecture with loadable objects at this time, the Windows installer currently comes without the csound6~ external. Use 6.06 or earlier versions until a solution is found.>>
Once you have installed the "csound6~" extension on any platform, and included the file in PD's search path if necessary, you should be able to call the csound6~ object in PD. Just open a PD window, put a new object, and type in "csound6~":
CONTROL DATA
You can send control data from PD to your Csound instrument via the keyword "control" in a message box. In your Csound code, you must receive the data via invalue or chnget. This is a simple example:
EXAMPLE 09A01_pdcs_control_in.csd
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
nchnls = 2
0dbfs = 1
ksmps = 8
giSine ftgen 0, 0, 2^10, 10, 1
instr 1
kFreq invalue "freq"
kAmp invalue "amp"
aSin oscili kAmp, kFreq, giSine
outs aSin, aSin
endin
</CsInstruments>
<CsScore>
i 1 0 10000
</CsScore>
</CsoundSynthesizer>
Save this file under the name "control.csd". Save a PD window in the same folder and create the following patch:
Note that for invalue channels, you first must register these channels by a "set" message. The usage of chnget is easier; a simple example can be found in this example in the csound6~ repository.
As you see, the first two outlets of the csound6~ object are the signal outlets for the audio channels 1 and 2. The third outlet is an outlet for control data (not used here, see below). The rightmost outlet sends a bang when the score has been finished.
LIVE INPUT
Audio streams from PD can be received in Csound via the inch opcode. The number of audio inlets created in the csound6~ object will depend on the number of input channels used in the Csound orchestra. The following .csd uses two audio inputs:
EXAMPLE 09A02_pdcs_live_in.csd
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
0dbfs = 1
ksmps = 8
nchnls = 2
instr 1
aL inch 1
aR inch 2
kcfL randomi 100, 1000, 1; center frequency
kcfR randomi 100, 1000, 1; for band pass filter
aFiltL butterbp aL, kcfL, kcfL/10
aoutL balance aFiltL, aL
aFiltR butterbp aR, kcfR, kcfR/10
aoutR balance aFiltR, aR
outch 1, aoutL
outch 2, aoutR
endin
</CsInstruments>
<CsScore>
i 1 0 10000
</CsScore>
</CsoundSynthesizer>
The corresponding PD patch is extremely simple:
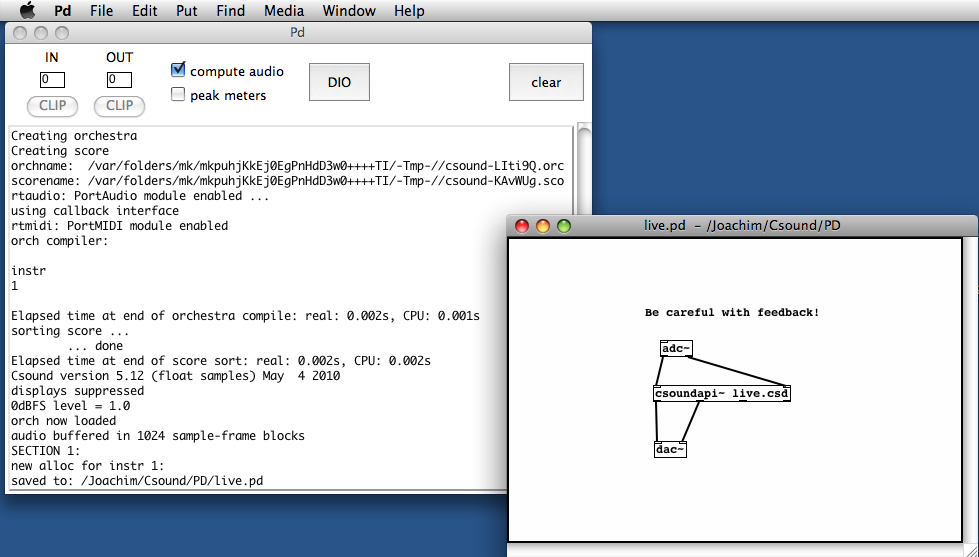
MIDI
The csound6~ object receives MIDI data via the keyword "midi". Csound is able to trigger instrument instances in receiving a "note on" message, and turning them off in receiving a "note off" message (or a note-on message with velocity=0). So this is a very simple way to build a synthesizer with arbitrary polyphonic output:
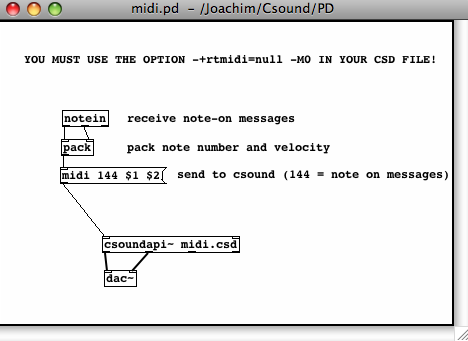
This is the corresponding midi.csd. It must contain the options -+rtmidi=null -M0 in the <CsOptions> tag. It is an FM synth in which the modulation index is defined according to the note velocity. The harder a key is truck, the higher the index of modulation will be; and therefore a greater number of stronger partials will be created. The ratio is calculated randomly between two limits, which can be adjusted.
EXAMPLE 09A03_pdcs_midi.csd
<CsOptions>
-+rtmidi=null -M0
</CsOptions>
<CsoundSynthesizer>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 8
nchnls = 2
0dbfs = 1
giSine ftgen 0, 0, 2^10, 10, 1
instr 1
iFreq cpsmidi ;gets frequency of a pressed key
iAmp ampmidi 8;gets amplitude and scales 0-8
iRatio random .9, 1.1; ratio randomly between 0.9 and 1.1
aTone foscili .1, iFreq, 1, iRatio/5, iAmp+1, giSine; fm
aEnv linenr aTone, 0, .01, .01; avoiding clicks at the end of a note
outs aEnv, aEnv
endin
</CsInstruments>
<CsScore>
f 0 36000; play for 10 hours
e
</CsScore>
</CsoundSynthesizer>
SCORE EVENTS
Score events can be sent from PD to Csound by a message with the keyword event. You can send any kind of score events, like instrument calls or function table statements. The following example triggers Csound's instrument 1 whenever you press the message box on the top. Different sounds can be selected by sending f events (building/replacing a function table) to Csound.

EXAMPLE 09A04_pdcs_events.csd
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
ksmps = 8
nchnls = 2
0dbfs = 1
seed 0; each time different seed
giSine ftgen 1, 0, 2^10, 10, 1; function table 1
instr 1
iDur random 0.5, 3
p3 = iDur
iFreq1 random 400, 1200
iFreq2 random 400, 1200
idB random -18, -6
kFreq linseg iFreq1, iDur, iFreq2
kEnv transeg ampdb(idB), p3, -10, 0
aTone oscili kEnv, kFreq, 1
outs aTone, aTone
endin
</CsInstruments>
<CsScore>
f 0 36000; play for 10 hours
e
</CsScore>
</CsoundSynthesizer>
CONTROL OUTPUT
If you want Csound to pass any control data to PD, you can use the opcode outvalue . You will receive this data at the second outlet from the right of the csound6~ object. The data are sent as a list with two elements. The name of the control channel is the first element, and the value is the second element. You can get the values by a route object or by a send/receive chain. This is a simple example:
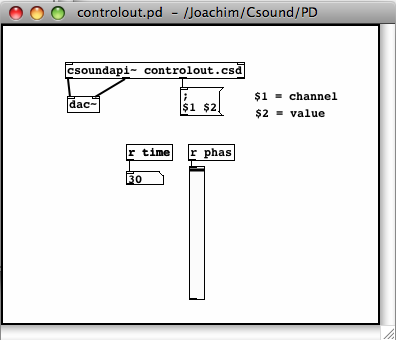
EXAMPLE 09A05_pdcs_control_out.csd
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
;Example by Joachim Heintz
sr = 44100
nchnls = 2
0dbfs = 1
ksmps = 8
instr 1
ktim times
kphas phasor 1
outvalue "time", ktim
outvalue "phas", kphas*127
endin
</CsInstruments>
<CsScore>
i 1 0 30
</CsScore>
</CsoundSynthesizer>
SEND/RECEIVE BUFFERS FROM PD TO CSOUND AND BACK
A PD array can be sent directly to Csound, and a Csound function table to PD. The message tabset [tabset array-name ftable-number] copies a PD array into a Csound function table. The message tabget [tabget array-name ftable-number] copies a Csound function table into a PD array. The example below should explain everything. Just choose another soundfile instead of "stimme.wav".
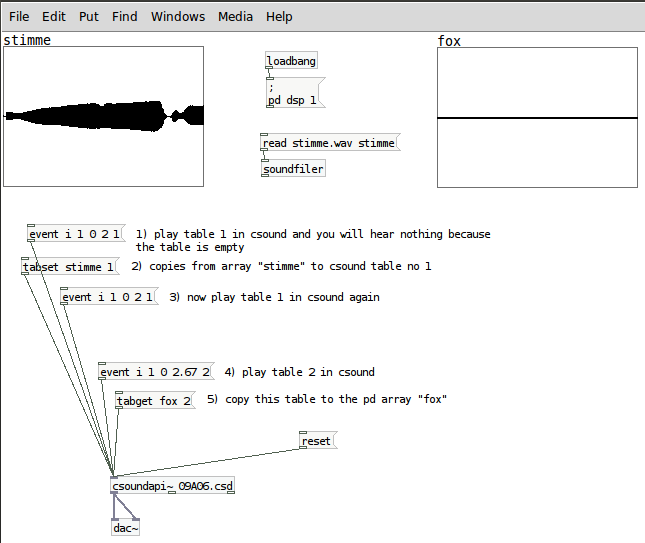
EXAMPLE 06A06_pdcs_tabset_tabget.csd
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 8
nchnls = 1
0dbfs = 1
giCopy ftgen 1, 0, -88200, 2, 0 ;"empty" table
giFox ftgen 2, 0, 0, 1, "fox.wav", 0, 0, 1
opcode BufPlay1, a, ipop
ifn, ispeed, iskip, ivol xin
icps = ispeed / (ftlen(ifn) / sr)
iphs = iskip / (ftlen(ifn) / sr)
asig poscil3 ivol, icps, ifn, iphs
xout asig
endop
instr 1
itable = p4
aout BufPlay1 itable
out aout
endin
</CsInstruments>
<CsScore>
f 0 99999
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
SETTINGS
Make sure that the Csound vector size given by the ksmps value, is not larger than the internal PD vector size. It should be a power of 2. I would recommend starting with ksmps=8. If there are performance problems, try to increase this value to 16, 32, or 64, i.e. ascending powers of 2.
The csound6~ object runs by default if you turn on audio in PD. You can stop it by sending a "run 0" message, and start it again with a "run 1" message.
You can recompile the .csd file of a csound6~ object by sending a "reset" message.
By default, you see all the messages of Csound in the PD window. If you do not want to see them, send a "message 0" message. "message 1" re-enables message printing.
If you want to open a new .csd file in the csound6~ object, send the message "open", followed by the path of the .csd file you want to load.
A "rewind" message rewinds the score without recompilation. The message "offset", followed by a number, offsets the score playback by that number of seconds.
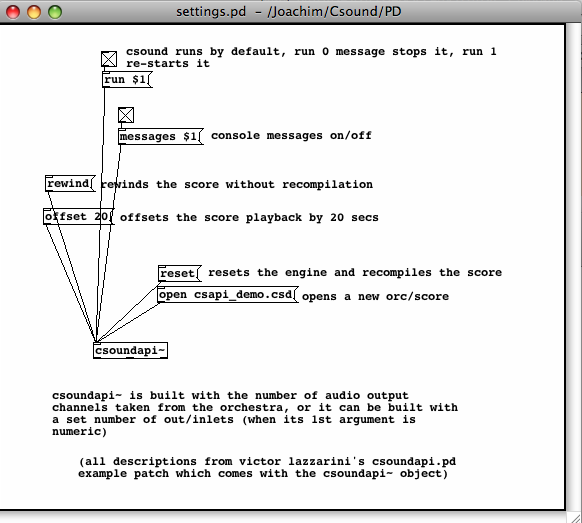
- This is the new name for Csound 6. In Csound 5 the name was csoundapi~. The different names make it possible to have both versions installed. Wherever in this chapter "csoundapi~" is used, it should work the same way as "csound6~" for Csound 6. ^
CSOUND IN MAXMSP
Csound can be embedded in a Max patch using the csound~ object. This allows you to synthesize and process audio, MIDI, or control data with Csound.
INSTALLING
The csound~ requires an installation of Csound. For Csound6, it should be a part of the main installer. If this is not the case, you should find an installer in Csound's file release folder, for instance as to Csound 6.02 here: http://sourceforge.net/projects/csound/files/csound6/Csound6.02/csound%7E_v1.1.1.pkg/download.
The next paragraphs were instructions for Csound5. They may now be obsolete.
INSTALLING ON MAC OS X
- Expand the zip file and navigate to binaries/MacOSX/.
- Choose an mxo file based on what kind of CPU you have (intel or ppc) and which type of floating point numbers are used in your Csound5 version (double or float). The name of the Csound5 installer may give a hint with the letters "f" or "d" or explicitly with the words "double" or "float". However, if you do not see a hint, then that means the installer contains both, in which case you only have to match your CPU type.
- Copy the mxo file to:
- Max 4.5: /Library/Application Support/Cycling '74/externals/
- Max 4.6: /Applications/MaxMSP 4.6/Cycling'74/externals/
- Max 5: /Applications/Max5/Cycling '74/msp-externals/
- Rename the mxo file to "csound~.mxo".
- If you would like to install the help patches, navigate to the help_files folder and copy all files to:
- Max 4.5: /Applications/MaxMSP 4.5/max-help/
- Max 4.6: /Applications/MaxMSP 4.6/max-help/
- Max 5: /Applications/Max5/Cycling '74/msp-help/
INSTALLING ON WINDOWS
- Expand the zip file and navigate to binaries\Windows\.
- Choose an mxe file based on the type of floating point numbers used in your Csound5 version (double or float). The name of the Csound5 installer may give a hint with the letters "f" or "d" or explicitly with the words "double" or "float".
- Copy the mxe file to:
- Max 4.5: C:\Program Files\Common Files\Cycling '74\externals\
- Max 4.6: C:\Program Files\Cycling '74\MaxMSP 4.6\Cycling '74\externals\
- Max 5: C:\Program Files\Cycling '74\Max 5.0\Cycling '74\msp-externals\
- Rename the mxe file to "csound~.mxe".
- If you would like to install the help patches, navigate to the help_files folder and copy all files to:
- Max 4.5: C:\Program Files\Cycling '74\MaxMSP 4.5\max-help\
- Max 4.6: C:\Program Files\Cycling '74\MaxMSP 4.6\max-help\
- Max 5: C:\Program Files\Cycling '74\Max 5.0\Cycling '74\msp-help\
KNOWN ISSUES
On Windows (only), various versions of Csound5 have a known incompatibility with csound~ that has to do with the fluid opcodes. How can you tell if you are affected? Here is how: if you stop a Csound performance (or it stops by itself) and you click on a non-MaxMSP or non-Live window and it crashes, then you are affected. Until this is fixed, an easy solution is to remove/delete fluidOpcodes.dll from your plugins or plugins64 folder. Here are some common locations for that folder:
- C:\Program Files\Csound\plugins
- C:\Program Files\Csound\plugins64
CREATING A CSOUND~ PATCH
- Create the following patch:
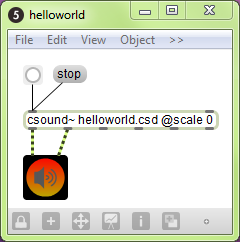
- Save as "helloworld.maxpat" and close it.
- Create a text file called "helloworld.csd" within the same folder as your patch.
- Add the following to the text file:
EXAMPLE 09B01_maxcs_helloworld.csd
<CsoundSynthesizer> <CsInstruments> ;Example by Davis Pyon sr = 44100 ksmps = 32 nchnls = 2 0dbfs = 1 instr 1 aNoise noise .1, 0 outch 1, aNoise, 2, aNoise endin </CsInstruments> <CsScore> f0 86400 i1 0 86400 e </CsScore> </CsoundSynthesizer> - Open the patch, press the bang button, then press the speaker icon.
At this point, you should hear some noise. Congratulations! You created your first csound~ patch.
You may be wondering why we had to save, close, and reopen the patch. This is needed in order for csound~ to find the csd file. In effect, saving and opening the patch allows csound~ to "know" where the patch is. Using this information, csound~ can then find csd files specified using a relative pathname (e.g. "helloworld.csd"). Keep in mind that this is only necessary for newly created patches that have not been saved yet. By the way, had we specified an absolute pathname (e.g. "C:/Mystuff/helloworld.csd"), the process of saving and reopening would have been unnecessary.
The "@scale 0" argument tells csound~ not to scale audio data between Max and Csound. By default, csound~ will scale audio to match 0dB levels. Max uses a 0dB level equal to one, while Csound uses a 0dB level equal to 32768. Using "@scale 0" and adding the statement "0dbfs = 1" within the csd file allows you to work with a 0dB level equal to one everywhere. This is highly recommended.
AUDIO I/O
All csound~ inlets accept an audio signal and some outlets send an audio signal. The number of audio outlets is determined by the arguments to the csound~ object. Here are four ways to specify the number of inlets and outlets:
- [csound~ @io 3]
- [csound~ @i 4 @o 7]
- [csound~ 3]
- [csound~ 4 7]
"@io 3" creates 3 audio inlets and 3 audio outlets. "@i 4 @o 7" creates 4 audio inlets and 7 audio outlets. The third and fourth lines accomplish the same thing as the first two. If you don't specify the number of audio inlets or outlets, then csound~ will have two audio inlets and two audio oulets. By the way, audio outlets always appear to the left of non-audio outlets. Let's create a patch called audio_io.maxpat that demonstrates audio i/o:
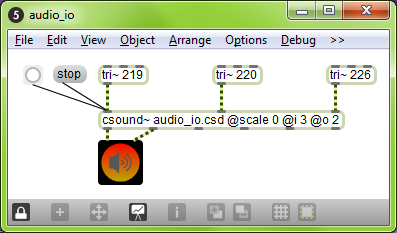
Here is the corresponding text file (let's call it audio_io.csd):
EXAMPLE 09B02_maxcs_audio_io.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Davis Pyon
sr = 44100
ksmps = 32
nchnls = 3
0dbfs = 1
instr 1
aTri1 inch 1
aTri2 inch 2
aTri3 inch 3
aMix = (aTri1 + aTri2 + aTri3) * .2
outch 1, aMix, 2, aMix
endin
</CsInstruments>
<CsScore>
f0 86400
i1 0 86400
e
</CsScore>
</CsoundSynthesizer>
In audio_io.maxpat, we are mixing three triangle waves into a stereo pair of outlets. In audio_io.csd, we use inch and outch to receive and send audio from and to csound~. inch and outch both use a numbering system that starts with one (the left-most inlet or outlet).
Notice the statement "nchnls = 3" in the orchestra header. This tells the Csound compiler to create three audio input channels and three audio output channels. Naturally, this means that our csound~ object should have no more than three audio inlets or outlets.
CONTROL MESSAGES
Control messages allow you to send numbers to Csound. It is the primary way to control Csound parameters at i-rate or k-rate. To control a-rate (audio) parameters, you must use and audio inlet. Here are two examples:
- control frequency 2000
- c resonance .8
Notice that you can use either "control" or "c" to indicate a control message. The second argument specifies the name of the channel you want to control and the third argument specifies the value.
The following patch and text file demonstrates control messages:
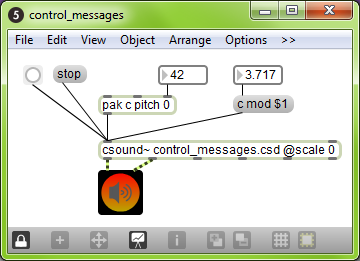
EXAMPLE 09B03_maxcs_control_in.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Davis Pyon
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
giSine ftgen 1, 0, 16384, 10, 1 ; Generate a sine wave table.
instr 1
kPitch chnget "pitch"
kMod invalue "mod"
aFM foscil .2, cpsmidinn(kPitch), 2, kMod, 1.5, giSine
outch 1, aFM, 2, aFM
endin
</CsInstruments>
<CsScore>
f0 86400
i1 0 86400
e
</CsScore>
</CsoundSynthesizer>
In the patch, notice that we use two different methods to construct control messages. The "pak" method is a little faster than the message box method, but do whatever looks best to you. You may be wondering how we can send messages to an audio inlet (remember, all inlets are audio inlets). Don't worry about it. In fact, we can send a message to any inlet and it will work.
In the text file, notice that we use two different opcodes to receive the values sent in the control messages: chnget and invalue. chnget is more versatile (it works at i-rate and k-rate, and it accepts strings) and is a tiny bit faster than invalue. On the other hand, the limited nature of invalue (only works at k-rate, never requires any declarations in the header section of the orchestra) may be easier for newcomers to Csound.
MIDI
csound~ accepts raw MIDI numbers in it's first inlet. This allows you to create Csound instrument instances with MIDI notes and also control parameters using MIDI Control Change. csound~ accepts all types of MIDI messages, except for: sysex, time code, and sync. Let's look at a patch and text file that uses MIDI:

EXAMPLE 09B04_maxcs_midi.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Davis Pyon
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
massign 0, 0 ; Disable default MIDI assignments.
massign 1, 1 ; Assign MIDI channel 1 to instr 1.
giSine ftgen 1, 0, 16384, 10, 1 ; Generate a sine wave table.
instr 1
iPitch cpsmidi
kMod midic7 1, 0, 10
aFM foscil .2, iPitch, 2, kMod, 1.5, giSine
outch 1, aFM, 2, aFM
endin
</CsInstruments>
<CsScore>
f0 86400
e
</CsScore>
</CsoundSynthesizer>
In the patch, notice how we're using midiformat to format note and control change lists into raw MIDI bytes. The "1" argument for midiformat specifies that all MIDI messages will be on channel one.
In the text file, notice the massign statements in the header of the orchestra. "massign 0,0" tells Csound to clear all mappings between MIDI channels and Csound instrument numbers. This is highly recommended because forgetting to add this statement may cause confusion somewhere down the road. The next statement "massign 1,1" tells Csound to map MIDI channel one to instrument one.
To get the MIDI pitch, we use the opcode cpsmidi. To get the FM modulation factor, we use midic7 in order to read the last known value of MIDI CC number one (mapped to the range [0,10]).
Notice that in the score section of the text file, we no longer have the statement "i1 0 86400" as we had in earlier examples. This is a good thing as you should never instantiate an instrument via both MIDI and score events (at least that has been this writer's experience).
Events
To send Csound events (i.e. score statements), use the "event" or "e" message. You can send any type of event that Csound understands. The following patch and text file demonstrates how to send events:
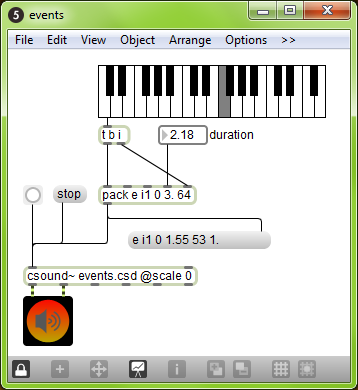
EXAMPLE 09B05_maxcs_events.csd
<CsoundSynthesizer>
<CsInstruments>
;Example by Davis Pyon
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
instr 1
iDur = p3
iCps = cpsmidinn(p4)
iMeth = 1
print iDur, iCps, iMeth
aPluck pluck .2, iCps, iCps, 0, iMeth
outch 1, aPluck, 2, aPluck
endin
</CsInstruments>
<CsScore>
f0 86400
e
</CsScore>
</CsoundSynthesizer>
In the patch, notice how the arguments to the pack object are declared. The "i1" statement tells Csound that we want to create an instance of instrument one. There is no space between "i" and "1" because pack considers "i" as a special symbol signifying an integer. The next number specifies the start time. Here, we use "0" because we want the event to start right now. The duration "3." is specified as a floating point number so that we can have non-integer durations. Finally, the number "64" determines the MIDI pitch. You might be wondering why the pack object output is being sent to a message box. This is good practice as it will reveal any mistakes you made in constructing an event message.
In the text file, we access the event parameters using p-statements. We never access p1 (instrument number) or p2 (start time) because they are not important within the context of our instrument. Although p3 (duration) is not used for anything here, it is often used to create audio envelopes. Finally, p4 (MIDI pitch) is converted to cycles-per-second. The print statement is there so that we can verify the parameter values.
CSOUND IN ABLETON LIVE
Csound can be used in Ableton Live through Max4Live. Max4Live is a toolkit which allows users to build devices for Live using Max/MSP. Please see the previous section on using Csound in Max/MSP for more details on how to use Csound in Live.
Cabbage can also be used to run Csound in Live, or any other audio plugin host. Please refer to the section titled 'Cabbage' in chapter 10.
D. CSOUND AS A VST PLUGIN
Csound can be built into a VST or AU plugin through the use of the Csound host API. Refer to the section on using the Csound API for more details.
If you are not well versed in low level computer programming you can just use Cabbage to create Csound based plugins. See the section titled 'Cabbage' in Chapter 10.
10 CSOUND FRONTENDS
CsoundQt
CsoundQt is a free, cross-platform graphical frontend to Csound. It features syntax highlighting, code completion and a graphical widget editor for realtime control of Csound. It comes with many useful code examples, from basic tutorials to complex synthesizers and pieces written in Csound. It also features an integrated Csound language help display.
CsoundQt (named QuteCsound until automn 2011) can be used as a code editor tailored for Csound, as it facilitates running and rendering Csound files without the need of typing on the command line using the Run and Render buttons.
In the widget editor panel, you can create a variety of widgets to control Csound. To link the value from a widget, you first need to set its channel, and then use the Csound opcodes invalue or chnget. To send values to widgets, e.g. for data display, you need to use the outvalue or chnset opcode.
CsoundQt also now implements the use of HTML and JavaScript code embedded in the optional <html> element of the CSD file. If this element is detected, CsoundQt will parse it out as a Web page, compile it, and display it in the 'HTML5 Gui' window. HTML code in this window can control Csound via a selected part of the Csound API that is exposed in JavaScript. This can be used to define custom user interfaces, display video and 3D graphics, generate Csound scores, and much more. See Chapter 12, Section H, Csound and Html for more information.
CsoundQt also offers convenient facilities for score editing in a spreadsheet like environment which can be transformed using Python scripting (see also chapter 12C).
You will find more detailed information and video tutorials in the CsoundQt home page at http://qutecsound.sourceforge.net.
Configuring CsoundQt
CsoundQt gives easy access to the most important Csound options and to many specific CsoundQt settings via its Configuration Panel. In particular the 'Run' tab offers many choices which have to be understood and set carefully.
The current version of CsoundQt's configuration settings should be found at http://qutecsound.sourceforge.net/pages/documentation.html. So the following descriptions may be outdated.
To open the configuration panel simply push the 'Configure' button. The configuration panel comprises 7 tabs. The available configurable parameters in each tab are described below for each tab.
Run
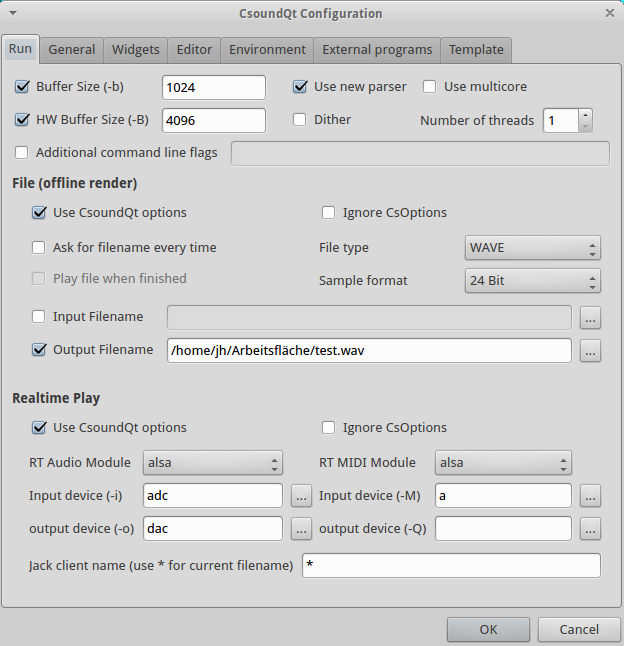
The settings at the top of the “Run” tab allow the user to define the command-line flags with which Csound is invoked.
Buffer Size (-b)
This defines the software buffer size (corresponding with the -b flag).
If you do not tick, CsoundQt will use the defaults.1
If you tick to enter an own value, these are some hints:
- Always use power-of-two values.
- Usually the ksmps block size is 1/4 or 1/2 of the software buffer size. If you use live input and output, it is most effective to set the software buffer size to an integer multiple of ksmps ("full duplex audio").
- Use smaller values (e.g. 128) for live performance (in particular with live input), as it will reduce the latency. Use larger values (e.g. 1024) for other cases, for instance playing sound files.
HW Buffer Size (-B)
This defines the hardware buffer size (corresponding with the -B flag).
If you do not tick, CsoundQt will use the defaults.2
If you tick to enter an own value, these are some hints:
- Always use a multiple integer of the software buffer size. A common relation is: Hardware Buffer Size = 4 * Software Buffer Size.
- The relation between software buffer size and hardware buffer size depends on the audio module.3
Use new parser
Tick this if you use Csound 5.14 or higher. This option has been introduced during the transition between the old and the new parser, and will disappear in future.
Use multicore /Number of threads
This option is only available when the new parser is enabled, and corresponds with the -j flag. For instance, ‘-j 2‘ will tell Csound to use 2 parallel processors when possible.
You should use this option with care. It may be also worth to state that using multiple threads will not in each case improve the performance. Whether it does or not depends on the structure of the csd file you run.
Dither
Switches on dithering (the --dither flag) for the conversion of audio from the internal resolution (now mostly 64 bit double precision float) to the output sample format (see below).
Additional command line flags
This enables the user to add any additional options not listed here. Only use if you know what you are doing!
File (offline render)
These options determine CsoundQt's behaviour if you render to file (by pushing the Render button or selecting the menu item Control -> Render to file).
Use CsoundQt options
Tick this to activate the CsoundQT options configured here.
Ignore CsOptions
Use this to ignore the option embedded in the <CsOptions> section of the csd files you are rendering.
NOTE that care must be taken to avoid inconsistencies between CsOptions and CsoundQt options. For beginners, it is recommended to tick "Ignore CsOptions" when the CsoundQT options are enabled. If you are a more experienced user, you can leave this unchecked to allow some additional options like -m128 to reduce Csound's printout.
NOTE that if you have checked "Use CsoundQt options" and have not checked "Ignore CsOptions", in the case of a conflict between both the CsoundQt options set in the configure panel will have the priority.
Ask for filename every time
Ask for a filename to render the performance to.
File type / Sample format
Use this to set the output file format.
Input Filename
Corresponds with the -i flag (Input soundfile name).
Output Filename
Corresponds with the -o flag for defining the output file name to which the sound is written.
Realtime Play
These options determine CsoundQt's behaviour if you push the Run button (or select the menu item Control -> Run Csound).
Use CsoundQt options
Tick this to activate the CsoundQT options configured here.
Ignore CsOptions
Use this to ignore the option embedded in the <CsOptions> section of the csd files you are running.
NOTE that care must be taken to avoid inconsistencies between CsOptions and CsoundQt options. For beginners, it is recommended to disable CsOptions when the CsoundQT options are enabled. If you are a more experienced user, you can leave this unchecked to allow some additional options like -m128 to reduce Csound's printout.
NOTE that if you have checked "Use CsoundQt options" and have not checked "Ignore CsOptions", in the case of a conflict between both the CsoundQt options set in the configure panel will have the priority.
RT Audio Module
This option is very much dependent on your operating system.
In case you experience crashes or have problems with the real time performance, it is worth to try another module.
The most common choices on the different operating systems are probably:
- For Linux, use alsa or jack.
- For OSX, use coreaudio or portaudio.
- For Windows, use portaudio.
Input device
This option selects the device you are using for real-time input, for instance from a microphone. (Note that you must have ticked "Use CsoundQt options" if you want Csound to use your selection.)
The usual (and most stable) choice here is adc. In this case Csound will use the device which has been selected as standard by your operating system.
If you want to use another device instead, click on the button at the right side. You will find a list of available devices and can choose one of them.
Output device
This option selects the device you are using for real-time output. (Note that you must have ticked "Use CsoundQt options" if you want Csound to use your selection.)
The usual (and most stable) choice here is dac. In this case Csound will use the device which has been selected as standard by your operating system.
If you want to use another device instead, click on the button at the right side. You will find a list of available devices and can choose one of them.
RT MIDI Module
This option is very much dependent on your operating system.
In case you experience problems with MIDI, it is worth to try another module. In case you do not use any MIDI at all, select none to get rid of one possible source of trouble.
The most common choices on the different operating systems are probably:
- For Linux, use alsa or portmidi.
- For OSX, use coremidi4 or portmidi.
- For Windows, use portmidi.
Input device
This option selects the device you are using for real-time MIDI input. (Note that you must have ticked "Use CsoundQt options" if you want Csound to use your selection.)
The usual choice here is a. In this case Csound will use all MIDI devices.
In case your RT MIDI Module does not support this option, click on the button at the right side. You will find a list of available devices and can choose one of them.
Output device
This option selects the device you are using for real-time MIDI output. (Note that you must have ticked "Use CsoundQt options" if you want Csound to use your selection.)
Jack client name
This option specifies the name for communicating with a Jack audio client. The default '*' means 'all' clients.
General

Run Utilities using:
This should be self-explanatory and is only meaningful if you run any of the Csound Utilities like sndinfo or the FFT analysis tool pvanal.
Interface language
Self-explanatory.
Performance tweaks
These are very important options in case you use CsoundQt for real-time usage and experience performance problems.
No messages to consoles
Tick this to disable any printout.
Disable recording and scopes
This refers to CsoundQt's internal Record facility and to the Scope widget.
Disable realtime score events
If you check this, you will not be able to send any live score event, for instance from a Button widget or the Live Event Sheet.
Disable python callback
If you do not use CsoundQt's internal Python scripting facility in real-time, you should check this to improve the overall performance.
Internal MIDI interface
The "Internal MIDI interface" is the MIDI device from which MIDI control messages are sent directly to the CsoundQt widgets. Have a look, for instance, in the properties of a Slider widget to see the MIDI CC number and the MIDI Channel to be specified.
Note that this does not set the input MIDI device for Csound itself (which has be explained above in Run -> RT MIDI Module -> Input device).
Record sample format
Defines the bit depth of the audio file to which CsoundQt records its real-time output, when using the Record button (or the 'record' option from the Control menu). For most cases 32bit float or 24bit formats are recommended. The former is particularly useful as it can hold ‘clipped‘ sample values, which can be later normalised.
Console
You can choose here how the Csound output console looks like.
Control message buffer size
If you do not not want to prevent CsoundQt from printing anything to the console at all (see above) but want to reduce this output for performance's sake, you can set here a limit.
There are some mixed options at the bottom of this tab:
Allow key repeats for sensekey
If you press a key on your computer for a long time, the key is repeated. This may or may not be useful for the sensekey opcode and can be decided here.
Debug mode for Live Event Sheet
Self-explanatory.
Allow simultaneous play
If checked, it allows you to play more than one csd tab simultansously.
Theme
Allows you to choose between the traditional ("fun") CsoundQt look, and a more serious ("boring") one.
Widgets
Enable Widgets
If not checked, you cannot use any of CsoundQt's widgets.
Save Widgets in csd file
Each csd file has a section for widgets and presets. These sections are hidden when you open your csd file in CsoundQt, but are visible in any text editor. So if you do not have checked this option, you will not see any of your widgets the next time you open your csd. So, only useful if you want to export a csd without the widget tags.
Show Widgets on play
If checked, the widget panel will pop up each time you push the Play button.
Show tooltips for widgets
Enables a useful feature which lets you see the channel name of a widget if you stay a moment on it with the computer mouse.
Enable FLTK
FLTK means a built-in (and somehow outdated) method of using widgets in Csound. As these widgets could conflict with CsoundQt's own widgets, you will usually uncheck this.
Run FLTK csds in Terminal
This lets you execute csd files which contain FLTK widgets without conflicting with CsoundQt.
Store Old Widget Format
CsoundQt started in using the file format for widgets from Matt Ingall's 'Mac Csound' for the sake of compatibility. Later it decided to use an own format; mainly for the build-in presets facility. When you check this option, CsoundQt will save the old Mac Csound widgets format in addition to the new proper CsoundQt widget format.
Open properties when creating widgets
Usually you will this have ticked, to enter your channel name and other properties when you create a widget.
Widgets are an independent window
CsoundQt consists of many subwindows except the main Editor panel: the Console, the Help (Manual), the Inspector, and so on. If you check this option, the widget panel will not be considered as one of them, but as independent window. This means that you cannot dock it by double-clicking on the top, like all the other subwindows, but it may have advantages anyhow, depending on your operating system and your configuration.
Font scaling / Font offset
Affects the way the fonts are shown for instance in a Label widget.
Editor
Only one option needs some explanation:
Autoplay files when launched from file
If ticked, a csd file will play immediately when opened.
Environment
There are some important settings here, along with some only for developers. We will focus on the options which can be important for all users.
Html Doc directory
This refers to the folder containing the Canonical Csound Manual. If you choose View -> Help Panel, and see nothing but a message like "not found!", you will have to set here the directory for the manual. Click on the browse button on the right side, and choose the folder where it is on your computer.5
SADIR (Sound Analysis Directory)
You can set here the directory in which Csound will seek for analysis files like .pvx files.
SSDIR (Sound Sample Directory)
This is very useful to set a folder for sound samples, for instance used by diskin. You can then refer to the sample only by name.
SFDIR (Sound File Directory)
To specify a directory for output files. This is usually be done in the 'Run' tab, as explained above (Output Filename).
INCDIR (Include Directory)
Specifies a directory for files which all called by the #include statement.
Favorite dir
Specifies a directory which will then appear under the menu as 'Favorites'.
Python script dir
Usually you will leave this empty so that CsoundQt links to the Python Scripts it comes with. Only specify if you build CsoundQt or want to change the scipts folder.
External Programs
Should be self-explanatory. 'Dot' is the executable from www.graphviz.org. It is used in CsoundQt for the Code Graph Viewer (View -> View Code Graph).
Template
This tab is useful as it allows the user to define a default template for new CSDs. Something like this can be a great timesaver:
- According to the relevant manual page, the defaults are 256 for Linux, 1024 for OSX and 4096 for Windows.^
- According to the manual, 1024 for Linux, 4096 for OSX and 16384 for Windows.^
- In the explanation of Victor Lazzarini (mail to Joachim Heintz, 19 march 2013):
"1. For portaudio, -B is only used to suggest a latency to the backend, whereas -b is used to set the actual buffersize.
2. For coreaudio, -B is used as the size of the internal circular buffer, and -b is used for the actual IO buffer size.
3. For jack, -B is used to determine the number of buffers used in conjunction with -b , num = (N + M + 1) / M. -b is the size of each buffer.
4. For alsa, -B is the size of the buffer size, -b is the period size (a buffer is divided into periods).
5. For pulse, -b is the actual buffersize passed to the device, -B is not used.
In other words, -B is not too significant in 1), not used in 5), but has a part to play in 2), 3) and 4), which is functionally similar." ^ - This options is only available in CsoundQt 0.7.3 or higher. For older versions, you must use the command line flag -+rtmidi=coremidi.^
- Or download the manual, if necessary, from sourceforge (currently http://sourceforge.net/projects/csound/files/csound5/csound5.19/manual/).^

The Cabbage Standalone Host.
The main Cabbage application that launches when you open Cabbage is known as the standalone host. This simple application 'hosts' Cabbage plugins in the same way any DAW hosts a plugin, but it is restricted to one plugin at a time (the host can be instantiated multiple times however). The host also features a source code editor for editing your code, and it also allows users to enter a GUI designer mode within which they can design interfaces using a simple drag-and-drop system. Access to the Csound output console and Reference Manual through the Cabbage host facilitate debugging and learning and the host also facilitates control of audio and MIDI settings used by Csound. If a user wishes to make their Cabbage patch available as a plugin for use within other software they can use the 'Export' option which will prompt them to export their instrument as an audio plugin. In addition to interacting with hosts via audio and MIDI connections, Cabbage plugins can also respond to host controls such as tempo, song position and play/stop status. The plugin formats are currently restricted to VST and Linux Native VST. Whilst the main purpose of the Cabbage standalone host is for prototyping and development, it can also be used as a fully blown production environment depending on the complexity of the hosted instrument.
An example of the GUI and source code editor.
Cabbage Instruments.
Cabbage instruments are nothing more than Csound instruments with an additional <Cabbage></Cabbage> section that exists outside of the <CsoundSynthesizer> tags. Each line of text in this section defines a GUI widget. Special identifiers can be used to control the look and behavior of each widget. This text ultimately defines how the graphical interface will look but recent innovations facilitate the modification of widget appearance from within the Csound orchestra. This opens up interesting possibilities including dynamically hiding and showing parts of the GUI and moving and resizing widgets during performance time. Instruments can be exported as either effects or synths. Effects process incoming audio, while synths won't produce any sound until they are triggered via the MIDI widget, or a MIDI keyboard. Cabbage makes no differentiation between synths and effects, but VST hosts do, so one must be careful when exporting instruments. A full list of available widgets, identifiers and parameters can be found in the Cabbage reference manual that comes with all Cabbage binaries.A Basic Cabbage Synthesiser
Example code to create the most basic Cabbage synthesiser is presented below. This instrument uses the MIDI interop command line flags to pipe MIDI data directly to p-fields in instrument 1. In this case all MIDI pitch data is sent directly to p4, and all MIDI amplitude data is sent to p5. (An alternative approach is to use Csounds opcodes cpsmidi, ampmidi etc. to read midi data into an instrument.) MIDI data sent on channel 1 will cause instrument 1 to play. Data sent on channel 2 will cause instrument 2 to play. If one prefers they may use the massign opcode rather than the MIDI interop flags, but regardless of what mechanism is used, you still need to declare "-+RTMIDI=NULL -M0" in the CsOptions.<Cabbage>
form size(400, 120), caption("Simple Synth"), pluginID("plu1")
keyboard bounds(0, 0, 380, 100)
</Cabbage>
<CsoundSynthesizer>
<CsOptions>
-n -d -+rtmidi=NULL -M0 --midi-key-cps=4 --midi-velocity-amp=5
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 64
nchnls = 2
0dbfs=1
instr 1
kenv linenr p5, 0.1, .25, 0.01
a1 oscil kenv*k1, p4, 1
outs a1, a1
endin
</CsInstruments>
<CsScore>
f1 0 1024 10 1
f0 3600
</CsScore>
</CsoundSynthesizer>
You will notice that a -n and -d are passed to Csound in the <CsOptions> section. -n stops Csound from writing audio to disk. This must be used when Cabbage is managing audio. If users wish to use Csound audio IO modules they need to disable Cabbage audio from the settings menu. The -d prevents any FLTK widgets from displaying. You will also notice that our instrument is stereo. ALL Cabbage instruments operate in stereo.
Controlling Your Instrument
The most obvious limitation to the above instrument is that users cannot interact directly with Csound. In order to do this one can use a Csound channel opcode and a Cabbage control such as a slider. Any control that is to interact with Csound must have a channel identifier.
When one supplies a channel name to the channel() identifier Csound will listen for data being sent on that channel through the use of the named channel opcodes. In order to retrieve data from the named channel bus in Csound one can use the chnget opcode. It is defined in the Csound reference manual as:
kval chnget Sname
Sname is the name of the channel. This same name must be passed to the channel() identifier in the corresponding <Cabbage> section. Cabbage only works with the chnget/chnset method of sending and receiving channel data. The invalue and outvalue opcodes are not supported.
The previous example can be modified so that a slider now controls the volume of our oscillator.
<Cabbage>
form size(400, 170), caption("Simple Synth"), pluginID("plu1")
hslider bounds(0, 110, 380, 50), channel("gain"), range(0, 1, .5), textBox(1)
keyboard bounds(0, 0, 380, 100)
</Cabbage>
<CsoundSynthesizer>
<CsOptions>
-n -d -+rtmidi=NULL -M0 --midi-key-cps=4 --midi-velocity-amp=5
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 64
nchnls = 2
0dbfs=1
instr 1
k1 chnget "gain"
kenv linenr p5, 0.1, 1, 0.1
a1 oscil kenv*k1, p4, 1
outs a1, a1
endin
</CsInstruments>
<CsScore>
f1 0 1024 10 1
f0 3600
</CsScore>
</CsoundSynthesizer>
In the example above we use a hslider control which is a horizontal slider. The bounds() identifier sets up the position and size of the widget. The most important identifier is channel(). It is passed a string "gain". This is the same string we pass to chnget in our Csound code. When a user moves the slider, the current position of the slider is sent to Csound on a channel named "gain". Without the channel() identifier no communication would take place between the Cabbage control and Csound. The keyboard widget can be used en lieu of a real MIDI keyboard when testing plugins. It is also possible to move Cabbage widgets from within the Csound orchestra using the chnset opcode.
A basic Cabbage effect
Cabbage effects are used to process incoming audio. To do so one must make sure they can access the incoming audio stream. Any of Csound's signal input opcodes can be used for this. The examples that come with Cabbage use both the ins and inch opcodes to retrieve the incoming audio signal. The following code is for a simple reverb unit. It accepts a stereo input and outputs a stereo signal.
<Cabbage>
form caption("Reverb") size(230, 130)
groupbox text("Stereo Reverb"), bounds(0, 0, 200, 100)
rslider channel("size"), bounds(10, 25, 70, 70), text("Size"), range(0, 2, 0.2)
rslider channel("fco"), bounds(70, 25, 70, 70), text("Cut-off"), range(0, 22000, 10000)
rslider channel("gain"), bounds(130, 25, 70, 70), text("Gain"), range(0, 1, 0.5)
</Cabbage>
<CsoundSynthesizer>
<CsOptions>
-d -n
</CsOptions>
<CsInstruments>
; Initialize the global variables.
sr = 44100
ksmps = 32
nchnls = 2
instr 1
kfdback chnget "size"
kfco chnget "fco"
kgain chnget "gain"
ainL inch 1
ainR inch 2
aoutL, aoutR reverbsc ainL, ainR, kfdback, kfco
outs aoutL*kgain, aoutR*kgain
endin
</CsInstruments>
<CsScore>
f1 0 4096 10 1
i1 0 1000
</CsScore>
</CsoundSynthesizer>
The above instrument uses 3 sliders to control the reverb size, the cut-off frequency for the internal low-pass filters, and the overall gain. The range() identifier is used with each slider to specify the min, max and starting value of the sliders. If you compare the two score sections in the above instruments you will notice that the synth instrument does not use any i-statement. Instead it uses an f0 3600. This tells Csound to wait for 3600 seconds before exiting. (In recent versions of Csound this step is no longer necessary to sustain performance.) Because synth instruments are controlled via MIDI we don’t need to use an i-statement in the score. In the audio effect example we use an i-statement with a long duration so that the effect runs without stopping for a long time, typically longer than a user session in a DAW.
Recent Innovations
gentable widget
The gentable widget can be used to display any Csound function table.
gentable views can be updated during performance in order to reflect any changes that may have been made to their contents by the Csound orchestra. Updating is actuated by using the gentable widget's so-called 'ident' channel (a channel that is used exclusively for changing the appearance of widgets and that is channel separate from the normal value channel).
It is also possible to modify the contents of a some function tables that are represented using gentable by clicking and dragging upon their GUI representations. This feature is a work in progress and is currently only available with GEN 02, 05 and 07.
soundfiler widget
Whilst audio files stored in GEN 01 function tables can be viewed using gentable it is more efficient (particularly with longer files) to do this using the 'soundfiler' widget.
soundfiler also facilitates zooming into and out of the viewed waveform and a portion of the waveform can be highlighted using click and drag. The start and end points of this highlighted region can be read into Csound and used, for example, as loop points. An example of this can be found in the Table3FilePlayer example in Cabbage's built-in examples in the File Players subsection. A 'scrubber' (a vertical line through the waveform) can also be displayed to indicate playback position.
Using soundfiler in combination with a button widget, we can open a browser and browse for a new sound file during performance. All of the examples in Examples>FilePlayers make use of this possibility.
widgetarray
The widgetarray identifier can be used with most widgets to generate large numbers of widgets in a single step.
The screenshot from the example shown above (which can be found in Cabbage's built-in examples in the 'FunAndGames' subsection) employs 300 image widgets to create the stars and the UFO and these are generated in a single line of code. Each individual widget can be addressed from within the Csound orchestra using a numbered identity channel, thereby they can be individually repositioned or modified in any other way. This process can be simplified by using looping procedures.
texteditor
The texteditor widget can be used to directly type in a string on the computer keyboard which can then be sent to Csound. An example use of this is to type in score events in real time (exemplified in the example RealTimeScoreEvents in the the 'Instructional' subsection in Cabbage's built-in examples.)
plants and popups
Cabbage 'plants' provides a convenient mechanism with which GUI elements which belong together in some way can be grouped. An example of this might be the various widgets pertaining to the values used by an envelope. Thereafter if becomes easier to modify the grouped widgets en masse: to move them somewhere else in the gui or to hide or reveal them completely.
An more elaborate function is to hold a plant in a completely separate GUI window that can be launched using a 'pop-up' button. An example of this is the 'Clavinet' instrument in the 'Synths' subsection in Cabbage's built-in examples.
Range sliders
A special type of slider (horizontal or vertical but not rotary 'r' type) employs two control knobs so that it can output two values.

This widget can be seen in action in the example DelayGrain in the 'Effects' subsection in Cabbage's built-in examples.
Reserved Channels
Reserved channels in Cabbage provide a means of reading in a variety of data beyond that of the Cabbage GUI widgets. This includes providing a means of reading in mouse position and mouse button activations and also tempo, song position and start/stop/record status (if used as a plugin within a host). These channels are read using the chnset opcode.
More information on any of these features can be found in the Cabbage reference manual which comes built into Cabbage or can be found here.
Where can I Download Cabbage?
Cabbage is hosted on GitHub, and pre-compiled binaries for Windows and OSX can be found at:
https://github.com/cabbageaudio/cabbage/releases
If you run Linux you will need to build Cabbage yourself, but instructions are included with the source code. You will need to have Csound installed.
BLUE
General Overview
Blue is a graphical computer music environment for composition, a versatile front-end to Csound. It is written in Java, platform-independent, and uses Csound as its audio engine. It provides higher level abstractions such as a graphical timeline for composition, GUI-based instruments, score generating SoundObjects like PianoRolls, python scripting, Cmask, Jmask and more. It is available for free (donation appreciated) at:
http://blue.kunstmusik.com
Organization of tabs and windows
Blue organizes all tasks that may arise while working with Csound within a single environment. Each task, be it score generation, instrument design, or composition is done in its own window. All the different windows are organized in tabs so that you can flip through easily and access them quickly.
In several places you will find lists and trees: All of your instruments used in a composition are numbered, named and listed in the Orchestra-window.
You will find the same for UDOs (User Defined Opcodes).
From this list you may export or import Instruments and UDOs from a library to the piece and vice versa. You may also bind several UDOs to a particular Instrument and export this instrument along with the UDOs it needs.
Editor
Blue holds several windows where you can enter code in an editor-like window. The editor-like windows are found for example in the Orchestra-window, the window to enter global score or the Tables-window to collect all the functions. There you may type in, import or paste text-based information. It gets displayed with syntax highlighting of Csound code.
Image: The Orchestra-window
The Score timeline as a graphical representation of the composition
The Score timeline allows for visual organization of all the used SoundObjects in a composition.
In the Score-window, which is the main graphical window that represents the composition, you may arrange the composition by arranging the various SoundObjects in the timeline. A SoundObject is an object that holds or even generates a certain amount of score-events. SoundObjects are the building blocks within blue's score timeline. SoundObjects can be lists of notes, algorithmic generators, python script code, Csound instrument definitions, PianoRolls, Pattern Editors, Tracker interfaces, and more. These SoundObjects may be text based or GUI-based as well, depending on their facilities and purposes.
Image: The timeline holding several Sound Objects. One SoundObject is selected and opened in the SoundObject-Editor-window
SoundObjects
To enable every kind of music production style and thus every kind of electronic music, blue holds a set of different SoundObjects. SoundObjects in blue can represent many things, whether it is a single sound, a melody, a rhythm, a phrase, a section involving phrases and multiple lines, a gesture, or anything else that is a perceived sound idea.
Just as there are many ways to think about music, each with their own model for describing sound and vocabulary for explaining music, there are a number of different SoundObjects in blue. Each SoundObject in blue is useful for different purposes, with some being more appropriate for expressing certain musical ideas than others. For example, using a scripting object like the PythonObject or RhinoObject would serve a user who is trying to express a musical idea that may require an algorithmic basis, while the PianoRoll would be useful for those interested in notating melodic and harmonic ideas. The variety of different SoundObjects allows for users to choose what tool will be the most appropriate to express their musical ideas.
Since there are many ways to express musical ideas, to fully allow the range of expression that Csound offers, blue's SoundObjects are capable of generating different things that Csound will use. Although most often they are used for generating Csound SCO text, SoundObjects may also generate ftables, instruments, user-defined opcodes, and everything else that would be needed to express a musical idea in Csound.
Means of modification of a SoundObject
First, you may set the start time and duration of every SoundObject "by hand" by typing in precise numbers or drag it more intuitively back and fourth on the timeline. This modifies and the position in time of a SoundObject, while stretching it modifies the outer boundaries of it and may even change the density of events it generates inside.
If you want to enter information into a SoundObject, you can open and edit it in a SoundObject editor-window.
But there is also a way to modify the “output” of a SoundObject, without having to change its content. The way to do this is using NoteProcessors.
By using NoteProcessors, several operations may be applied onto the parameters of a SoundObject. NoteProcessors allow for modifying the SoundObjects score results, i.e. adding 2 to all p4 values, multiplying all p5 values by 6, etc. These NoteProcessors can be chained together to manipulate and modify objects to achieve things like transposition, serial processing of scores, and more.
Finally the SoundObjects may be grouped together and organized in larger-scale hierarchy by combining them to PolyObjects.
Polyobject are objects, which hold other SoundObjects, and have timelines in themselves. Working within them on their timelines and outside of them on the parent timeline helps organize and understand the concepts of objective time and relative time between different objects.
Instruments with a graphical interface
Instruments and effects with a graphical interface may help to increase musical workflow. Among the instruments with a graphical user interface there are BlueSynthBuilder (BSB)-Instruments, BlueEffects and the blue Mixer.
BlueSynthBuilder (BSB)-Instruments
The BlueSynthBuilder (BSB)-Instruments and the BlueEffects work like conventional Csound instruments, but there is an additional opportunity to add and design a GUI that may contain sliders, knobs, textfields, pull-down menus and more. You may convert any conventional Csound Instrument automatically to a BSB-Instrument and then add and design a GUI. 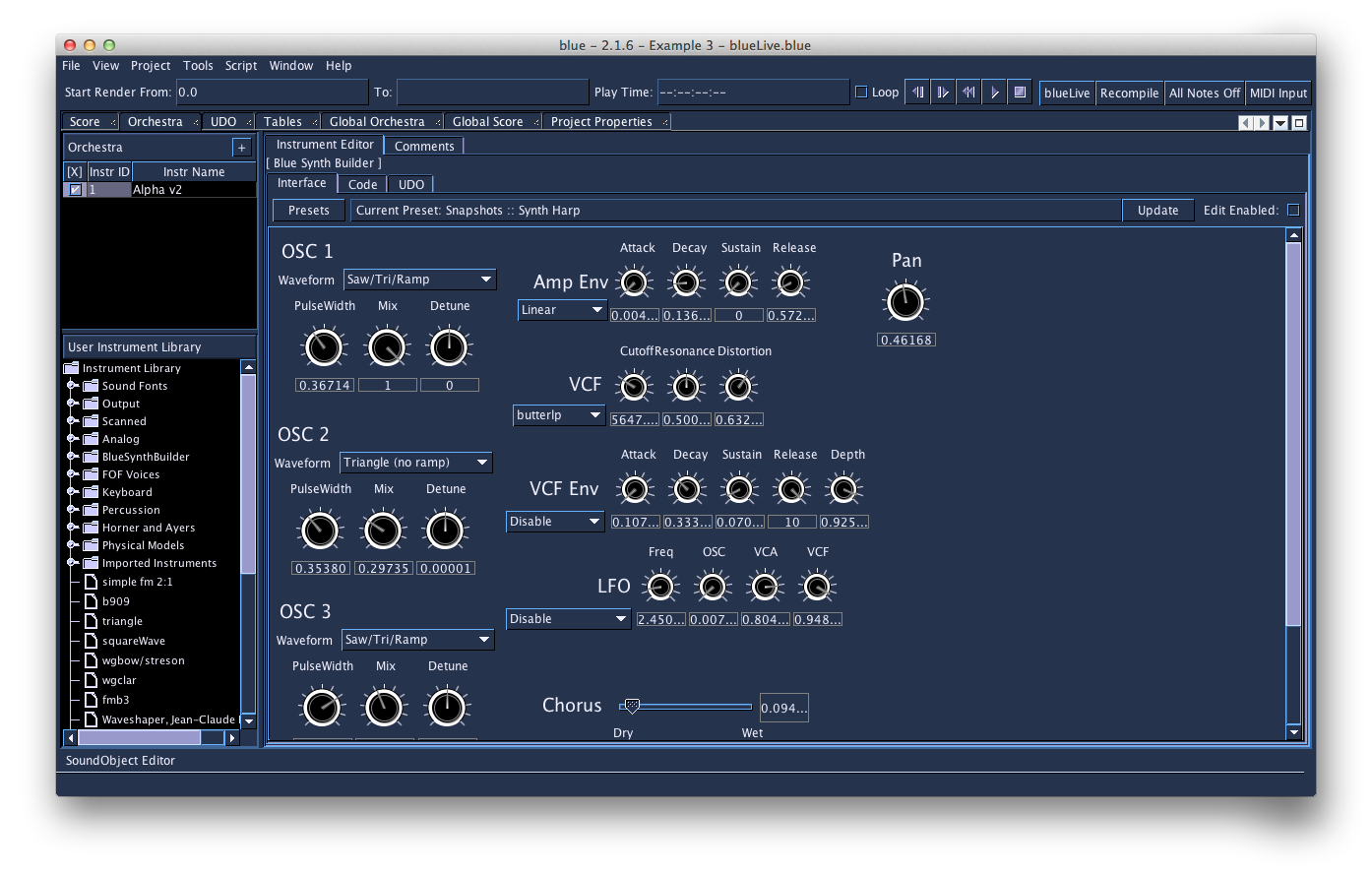
Image: The interface of a BSB-Instrument.
blue Mixer
Blue's graphical mixer system allows signals generated by instruments to be mixed together and further processed by Blue Effects. The GUI follows a paradigm commonly found in music sequencers and digital audio workstations.
The mixer UI is divided into channels, sub-channels, and the master channel. Each channel has a fader for applying level adjustments to the channel's signal, as well as bins pre- and post-fader for adding effects. Effects can be created on the mixer, or added from the Effects Library.
Users can modify the values of widgets by manipulating them in real-time, but they can also draw automation curves to compose value changes over time.
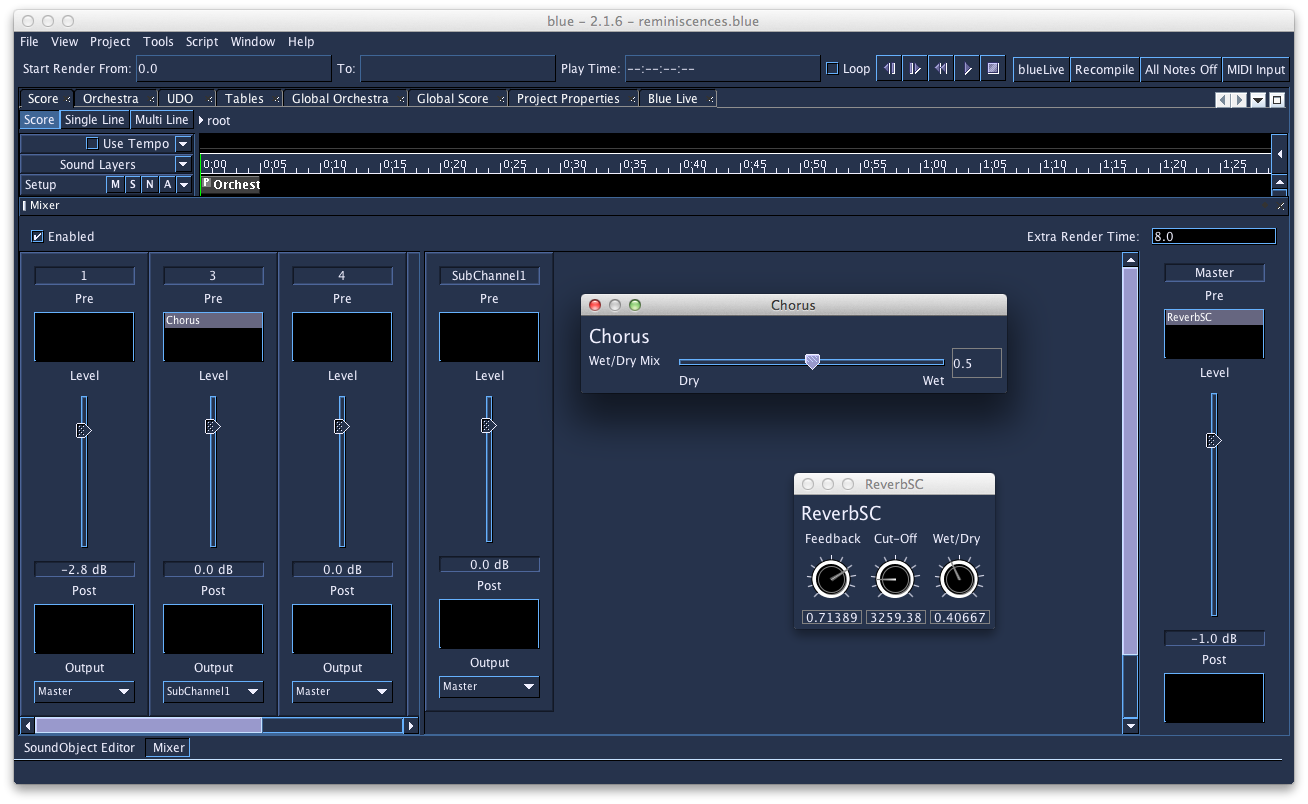
Image: The BlueMixer
Automation
For BSB-Instruments, blueMixer and blueEffects it is possible to use Lines and Graphs within the score timeline to enter and edit parameters via a line. In Blue, most widgets in BlueSynthBuilder and Effects can have automation enabled. Faders in the Mixer can also be automated.
Editing automation is done in the Score timeline. This is done by first selecting a parameter for automation from the SoundLayer's “A” button's popup menu, then selecting the Single Line mode in the Score for editing individual line values.
Using Multi-Line mode in the score allows the user to select blocks of SoundObjects and automations and move them as a whole to other parts of the Score.
Thus the parameters of these instruments with a GUI may be automatized and controlled via an editable graph in the Score-window.
Libraries
blue features also libraries for instruments, SoundObjects, UDOs, Effects (for the blueMixer) and the CodeRepositoryfor code snippets. All these libraries are organized as lists or trees. Items of the library may be imported to the current composition or exported from it to be used later in other pieces.
The SoundObject library allows for instantiating multiple copies of a SoundObject, which allows for editing the original object and updating all copies. If NoteProcessors are applied to the instances in the composition representing the general structure of the composition you may edit the content of a SoundObject in the library while the structure of the composition remains unchanged. That way you may work on a SoundObject while all the occurrences in the composition of that very SoundObject are updated automatically according the changes done in the library.
The Orchestra manager organizes instruments and functions as an instrument librarian.
There is also an Effects Library and a Library for the UDOs
Other Features
- blueLive - work with SoundObjects in realtime to experiment with musical ideas or performance.
- SoundObject freezing - frees up CPU cycles by pre-rendering SoundObjects
- Microtonal supportusing scales defined in the Scala scale format, including a microtonal PianoRoll, Tracker, NoteProcessors, and more.
WinXound
WinXound is a free and open-source Front-End GUI Editor for CSound 6, CSoundAV,
CSoundAC, with Python and Lua support, developed by Stefano Bonetti.
It runs on Microsoft Windows, Apple Mac OsX and Linux.
WinXound is optimized to work with the CSound 6 compiler.
WinXound Features:
- Edit CSound, Python and Lua files (csd, orc, sco, py, lua) with Syntax Highlight and Rectangular Selection;
- Run CSound, CSoundAV, CSoundAC, Python and Lua compilers;
- Run external language tools (QuteCsound, Idle, or other GUI Editors);
- CSound analysis user friendly GUI;
- Integrated CSound manual help;
- Possibilities to set personal colors for the syntax highlighter;
- Convert orc/sco to csd or csd to orc/sco;
- Split code into two windows horizontally or vertically;
- CSound csd explorer (File structure for Tags and Instruments);
- CSound Opcodes autocompletion menu;
- Line numbers;
- Bookmarks;
- ...and much more ... (Download it!)
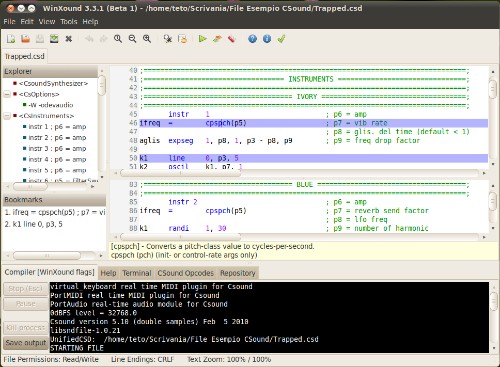
Web Site and Contacts:
- Web: winxound.codeplex.com
- Email: stefano_bonetti@tin.it (or stefano_bonetti@alice.it)
REQUIREMENTS
System requirements for Microsoft Windows:
- Supported: Xp, Vista, Seven (32/64 bit versions);
- (Note: For Windows Xp you also need the Microsoft Framework .Net version 2.0 or major. You can download it from www.microsoft.com site);
- CSound 6: http://sourceforge.net/projects/csound - (needed for CSound and LuaJit compilers);
- Not requested but suggested: CSoundAV by Gabriel Maldonado (http://www.csounds.com/maldonado/);
- Requested to work with Python: Python compiler (http://www.python.org/download/)
- Osx 10.5 or major;
- CSound 6: http://sourceforge.net/projects/csound - (needed for CSound compiler);
System requirements for Linux:
- Gnome environment or libraries;
- Please, read carefully the "ReadMe" file in the source code.
INSTALLATION AND USAGE
Microsoft Windows Installation and Usage:
- Download and install the Microsoft Framework .Net version 2.0 or major (only for Windows Xp);
- Download and install the latest version of CSound 6 (http://sourceforge.net/projects/csound);
- Download the WinXound zipped file, decompress it where you want (see the (*)note below), and double-click on "WinXound_Net" executable;
- (*)note: THE WINXOUND FOLDER MUST BE LOCATED IN A PATH WHERE YOU HAVE FULL READ AND WRITE PERMISSION (for example in your User Personal folder).
- Download and install the latest version of CSound 6 (http://sourceforge.net/projects/csound);
- Download the WinXound zipped file, decompress it and drag WinXound.app to your Applications folder (or where you want). Launch it from there.
Linux Installation and Usage:
- Download and install the latest version of CSound 6 for your distribution;
- Ubuntu (32/64 bit): Download the WinXound zipped file, decompress it in a location where you have the full read and write permissions;
- To compile the source code:
1) Before to compile WinXound you need to install:
- gtkmm-2.4 (libgtkmm-2.4-dev) >= 2.12
- vte (libvte-dev)
- webkit-1.0 (libwebkit-dev)
2) To compile WinXound open the terminal window, go into the uncompressed "winxound_gtkmm" directory and type:
./preconfigure
./configure
(make clean)
make
3) To use WinXound without installing it:
make standalone
./bin/winxound
[Note: WinXound folder must be located in a path where you have full read and write permission.]
4) To install WinXound:
make install
Source Code:
- Windows: The source code is written in C# using Microsoft Visual Studio C# Express Edition 2008.
- OsX: The source code is written in Cocoa and Objective-C using XCode 3.2 version.
- Linux: The source code is written in C++ (Gtkmm) using Anjuta.
Note: The TextEditor is entirely based on the wonderful SCINTILLA text control by Neil Hodgson (http://www.scintilla.org).
Screenshots:
Look at: winxound.codeplex.com
Many thanks for suggestions and debugging help to Roberto Doati, Gabriel Maldonado, Mark Jamerson, Andreas Bergsland, Oeyvind Brandtsegg, Francesco Biasiol, Giorgio Klauer, Paolo Girol, Francesco Porta, Eric Dexter, Menno Knevel, Joseph Alford, Panos Katergiathis, James Mobberley, Fabio Macelloni, Giuseppe Silvi, Maurizio Goina, Andrés Cabrera, Peiman Khosravi, Rory Walsh and Luis Jure.
CSOUND VIA TERMINAL
Whilst many of us now interact with Csound through one of its many front-ends which provide us with an experience more akin the that of mainstream software, new-comers to Csound should bear in mind that there was a time when the only way running Csound was from the command line using the Csound command. In fact we must still run Csound in this way but front-ends do this for us usually via some toolbar button or widget. Many people still prefer to interact with Csound from a terminal window and feel this provides a more 'naked' and honest interfacing with the program. Very often these people come from the group of users who have been using Csound for many years, form the time before front-ends. It is still important for all users to be aware of how to run Csound from the terminal as it provides a useful backup if problems develop with a preferred front-end.
The Csound Command
The Csound command follows the format:
csound [performance_flags] [input_orc/sco/csd]
Executing 'csound' with no additional arguments will run the program but after a variety of configuration information is printed to the terminal we will be informed that we provided "insufficient arguments" for Csound to do anything useful. This action can still be valid for first testing if Csound is installed and configured for terminal use, for checking what version is installed and for finding out what performance flags are available without having to refer to the manual.
Performance flags are controls that can be used to define how Csound will run. All of these flags have defaults but we can make explicitly use flags and change these defaults to do useful things like controlling the amount of information that Csound displays for us while running, activating a MIDI device for input, or altering buffer sizes for fine tuning realtime audio performance. Even if you are using a front-end, command line flags can be manipulated in a familiar format usually in 'settings' or 'preferences' menu. Adding flags here will have the same effect as adding them as part of the Csound command. To learn more about Csound's command line flags it is best to start on the page in the reference manual where they are listed and described by category.
Command line flags can also be defined within the <CsOptions> </CsOptions> part of a .csd file and also in a file called .csoundrc which can be located in the Csound home program directory and/or in the current working directory. Having all these different options for where esentially the same information is stored might seem excessive but it is really just to allow flexibiliy in how users can make changes to how Csound runs, depending on the situation and in the most efficient way possible. This does however bring up one one issue in that if a particular command line flag has been set in two different places, how does Csound know which one to choose? There is an order of precedence that allows us to find out.
Beginning from its own defaults the first place Csound looks for additional flag options is in the .csoundrc file in Csound's home directory, the next is in a .csoundrc file in the current working directory (if it exists), the next is in the <CsOptions> of the .csd and finally the Csound command itself. Flags that are read later in this list will overwrite earlier ones. Where flags have been set within a front-end's options, these will normally overwrite any previous instructions for that flag as they form part of the Csound command. Often a front-end will incorporate a check-box for disabling its own inclusion of flag (without actually having to delete them from the dialogue window).
After the command line flags (if any) have been declared in the Csound command, we provide the name(s) of out input file(s) - originally this would have been the orchestra (.orc) and score (.sco) file but this arrangement has now all but been replaced by the more recently introduced .csd (unified orchestra and score) file. The facility to use a separate orchestra and score file remains however.
For example:
Csound -d -W -osoundoutput.wav inputfile.csd
will run Csound and render the input .csd 'inputfile.csd' as a wav file ('-W' flag) to the file 'soundoutput.wav' ('-o' flag). Additionally displays will be suppressed as dictated by the '-d' flag. The input .csd file will need to be in the current working directory as no full path has been provided. the output file will be written to the current working directory of SFDIR if specified.
WEB BASED CSOUND
Using Csound via UDP with the --port Option
The --port=N option allows users to send orchestras to be compiled on-the-fly by Csound via UDP connection. This way, Csound can be started with no instruments, and will listen to messages sent to it. Many programs are capable of sending UDP messages, and scripting languages, such as Python, can also be used for this purpose. The simplest way of trying out this option is via the netcat program, which can be used in the terminal via the nc command.
Let's explore this as an example of the --port option. First, Csound is started with the following command:
$ csound -odac --port=1234
Alternatively, if using a frontend such as CsoundQT, it is possible run an empty CSD, with the --port in its CsOptions field:
<CsoundSynthesizer> <CsOptions> --port=1234 </CsOptions> <CsInstruments> </CsInstruments> <CsScore> </CsScore> </CsoundSynthesizer>
This will start Csound in a daemon mode, waiting for any UDP messages in port 1234. Now with netcat, orchestra code can be sent to Csound. A basic option is to use it interactively in the terminal, with a heredocument command (<<) to indicate the end of the orchestra we are sending:
$ nc -u 127.0.0.1 1234 << EOF > instr 1 > a1 oscili p4*0dbfs,p5 > out a1 > endin > schedule 1,0,1,0.5,440 > EOF
Csound will respond with a 440Hz sinewave. The ctl-c key combination can be used to close nc and go back to the shell prompt. Alternatively, we could write our orchestra code to a file and then send it to Csound via
the following command (orch is the name of our file):
$ nc -u 127.0.0.1 1234 < orch
Csound performance can be stopped in the usual way via ctl-c in the terminal, or through the dedicated
transport controls in a frontend. We can also close the server it via a special UDP message:
ERROR WITH MACRO close
However, this will not close Csound, but just stop the UDP server.
pNaCl - Csound for Portable Native Client
Native Client (NaCl) is a sandboxing technology developed by Google that allows C/C++ modules to extend the support provided by HTML5. Portable Native Client (pNaCl) is one of the toolchains in the NaCl SDK (the others are newlib and glibc). The advantage of pNaCl over the other options is that it only requires a single module to be built for all supported architectures.
The other major advantage is that pNaCl is, as of Google Chrome 31, enabled by default in the browser. This means that users just need to load a page containing the pNaCl application and it will work. pNaCl modules are compiled to llvm bytecode that is translated to a native binary by the browser. To check whether your version of Chrome supports pNaCl, use the following address:
chrome://nacl
The pNaCl Csound implementation allows users to embed the system in web pages. With a minimal use of Javascript, it is possible to create applications and frontends for Csound, to be run inside a web browser (Chrome, Chromium).
A binary package for pNaCl-Csound can be found in the Csound releases http://sourceforge.net/projects/csound/files/csound6
Running the example application
NaCl pages need to be served over http, which means they will not work when opened as local files. For this you will need a http server. A minimal one, written in Python, can be found in the NaCl SDK https://developer.chrome.com/native-client/sdk/download.
Csound pNaCl module reference
The interface to Csound is found in the csound.js javascript file. Csound is ready on module load, and can accept control messages from then on.
Control functions
The following control functions can be used to interact with Csound:
- csound.Play() - starts performance
- csound.PlayCsd(s) - starts performance from a CSD file s, which can be in ./http/ (ORIGIN server) or ./local/ (local sandbox).
- csound.RenderCsd(s) - renders a CSD file s, which can be in ./http/ (ORIGIN server) or ./local/ (local sandbox), with no RT audio output. The “finished render” message is issued on completion.
- csound.Pause() - pauses performance
- csound.StartAudioInput() - switches on audio input (available in Chrome version 36 onwards)
- csound.CompileOrc(s) - compiles the Csound code in the string s
- csound.ReadScore(s) - reads the score in the string s (with preprocessing support)
- csound.Event(s) - sends in the line events contained in the string s (no preprocessing)
- csound.SetChannel(name, value) - sends the control channel name the value value.
- csound.SetStringChannel(name, string) - sends the string channel name the string string.
- csound.SetTable(num, pos, value) - sets the table name at index pos the value value.
- csound.RequestTable(num) - requests the table data for table num. The “Table::Complete” message is issued on completion.
- csound.GetTableData() - returns the most recently requested table data as an ArrayObject.
- MIDIin(byte1, byte2, byte3) - sends a MIDI in message to Csound.
- NoteOn(channel,number,velocity) - sends a Note ON message to Csound.
- NoteOff(channel,number,velocity) - sends a Note OFF message to Csound.
- PolyAftertouch(channel,number,aftertouch) - sends a polyphonic aftertouch message to Csound.
- ControlChange(channel,control,amount) - sends a control change message to Csound.
- ProgramChange(channel,control) - sends a program change message to Csound.
- Aftertouch(channel,amount) - sends a mono aftertouch message to Csound.
- PitchBend(channel,fine,coarse) - sends a pitchbend message to Csound
Filesystem functions
In order to facilitate access to files, the following filesystem functions can be used:
- csound.CopyToLocal(src, dest) - copies the file src in the ORIGIN directory to the local file dest, which can be accessed at ./local/dest. The “Complete” message is issued on completion.
- csound.CopyUrlToLocal(url,dest) - copies the url url to the local file dest, which can be accessed at ./local/dest. Currently only ORIGIN and CORS urls are allowed remotely, but local files can also be passed if encoded as urls with the webkitURL.createObjectURL() javascript method. The “Complete” message is issued on completion.
- csound.RequestFileFromLocal(src) - requests the data from the local file src. The “Complete” message is issued on completion.
- csound.GetFileData() - returns the most recently requested file data as an ArrayObject.
Callbacks
The csound.js module will call the following window functions when it starts:
- function moduleDidLoad(): this is called as soon as the module is loaded
- function handleMessage(message): called when there are messages from Csound (pnacl module). The string message.data contains the message.
- function attachListeners(): this is called when listeners for different events are to be attached.
You should implement these functions in your HTML page script, in order to use the Csound javascript interface. In addition to the above, Csound javascript module messages are always sent to the HTML element with id=‘console’, which is normally of type <div> or <textarea>.
Example
Here is a minimal HTML example showing the use of Csound.
<!DOCTYPE html>
<html>
<!--
Csound pnacl minimal example
Copyright (C) 2013 V Lazzarini
-->
<head>
<title>Minimal Csound Example</title>
<script type="text/javascript" src="csound.js"></script>
<script type="text/javascript">
// called by csound.js
function moduleDidLoad() {
csound.Play();
csound.CompileOrc(
"instr 1 \n" +
"icps = 440+rnd(440) \n" +
"chnset icps, \"freq\" \n" +
"a1 oscili 0.1, icps\n" +
"outs a1,a1 \n" +
"endin");
document.getElementById("tit").innerHTML = "Click on the page below to play";
}
function attachListeners() {
document.getElementById("mess").
addEventListener("click",Play);
}
function handleMessage(message) {
var mess = message.data;
if(mess.slice(0,11) == "::control::") {
var messField = document.getElementById("console")
messField.innerText = mess.slice(11);
}
else {
var messField = document.getElementById("mess")
messField.innerText += mess;
csound.RequestChannel("freq");
}
}
// click handler
function Play() {
csound.Event("i 1 0 5");
}
</script>
</head>
<body>
<div id="console"></div>
<h3 id="tit"> </h3>
<div id="mess">
</div>
<!--pNaCl csound module-->
<div id="engine"></div>
</body>
</html>
Limitations
The following limitations apply:
- MIDI is implemented so that Csound MIDI opcodes can be used. MIDI hardware interface needs to be provided in Javascript by another library (e.g. WebMIDI).
- no plugins, as pNaCl does not support dlopen() and friends. This means some opcodes are not available as they reside in plugin libraries. It might be possible to add some of these opcodes statically to the Csound pNaCl library in the future.
More information on Csound for pNaCl can be found http://vlazzarini.github.io/.
libcsound.js - Csound as a Javascript Library
Introduction
The javascript build of Csound allows any standards compliant web browser to run an instance of Csound in a web page without the need for plugins or add ons. This is made possible by using Emscripten, a program that can convert software written in C (such as Csound) into Javascript, allowing it to be run natively within any web browser that supports modern web standards.
Caveats
The javascript build of Csound is currently in early stages of development and therefore there are a number of caveats and limitations with its current implementation which should be noted.
-
Emscripten generates a highly optimisable subset of Javascript called asm.js. This allows Javascript engines which have been optimised for this subset to achieve substantial performance increases over other Javascript engines. At this time the only Javascript engine that supports asm.js optimisations is the Spider Monkey engine which is part of Firefox. Therefore the Emscripten build of Csound will perform best on the current version of Firefox.
-
At this time, due to the design of the Web Audio API, the Csound javascript library can only execute within the main thread of a web page. This means that it must pause execution of any performance when any other process that uses the main thread (such as the UI) needs to execute. This can cause dropouts and/or glitching of the audio during a performance.
-
As this project is in its infancy, there are a minimal number of routines implemented so far in order to instantiate, compile and perform a .csd file. Additional routines will be added over time as the project matures.
Getting libcsound.js
The javascript build of Csound now comes as part of the regular distribution of the Csound source code. It can be found in the emscripten folder which also contains a markdown file that gives the instructions on how to compile the javascript library.
Using libcsound.js
In order to demonstrate how to use the Csound javascript library, what follows is a tutorial which shows the steps necessary to create a simple website that can open .csd files, compile them, and play them back from the browser.
Create a simple website
First create a new folder for the website and copy the libcsound.js and libcsound.js.mem files from the emscripten/dist directory into the new websites directory. Next, create an index.html file at the top level of the new websites directory that contains the following minimal html code:
<html>
<head>
<meta http-equiv="content-type" content="text/html; charset=utf-8">
</head>
<body>
</body>
</html>Instantiate Csound
We need to write some Javascript to create an instance of CsoundObj, so within the body tags ad new script tags and insert the following code:
<html>
<head>
<meta http-equiv="content-type" content="text/html; charset=utf-8">
</head>
<body>
<script src="libcsound.js"></script>
<script>
Module['noExitRuntime'] = true;
Module['_main'] = function() {
var csoundObj = new CsoundObj();
};
</script>
</body>
</html>The Module functions within this code are related to how emscripten built javascript libraries execute when a webpage is loaded. The noExitRuntime variable sets whether the emscripten runtime environment is exited once the main function has finished executing. The _main variable is actually a function that is executed as soon as the webpage has finished loading. Csound itself is instantiated using a constructor for the CsoundObj object. This object provides all the methods for directly interacting with the current running instance of csound.
The Javascript console of the web browser should now show some messages that give the version number of Csound, the build date and the version of libsndfile being used by Csound.
Upload .csd file to Javascript File System
In order to run a .csd file from the Csound javascript library, we first need to upload the file from the local file system to the javascript virtual file system. In the emscripten/examples directory there is the FileManager.js file that provides an object which greatly simplifies the process of uploading files to the virtual file system. Copy FileManager.js to the root directory of the web page.
<html>
<head>
<meta http-equiv="content-type" content="text/html; charset=utf-8">
</head>
<body>
<script src="libcsound.js"></script>
<script src="FileManager.js"></script>
<script>
Module['noExitRuntime'] = true;
Module['_main'] = function() {
var csoundObj = new CsoundObj();
var fileManger = new FileManager(['csd'], console.log);
fileManger.fileUploadFromServer("test.csd", function() {
csoundObj.compileCSD("test.csd");
});
};
</script>
</body>
</html>
As can be seen in the code above, the file manager is instantiated with two arguments. The first argument is an array of strings which tells the file manager instance which file extensions that are permitted to be uploaded. The second argument is the function with which the file manger will print error messages, in this case it will print to the javascript console. The file managers upload method also takes two arguments. The first argument is the files path relative to the website root directory and the second is the function to execute when the file has been successfully uploaded. In this case when the file has been uploaded csound will compile the .csd file.
If the web page is reloaded now, the file test.csd will be uploaded to the javascript file system and csound will compile it making it ready for performance.
Running Csound
Once the .csd file has been compiled csound can execute a performance. In the following code we will create an html button and add some code to the button so that when pressed it will run a performance of csound.
<html>
<head>
<meta http-equiv="content-type" content="text/html; charset=utf-8">
</head>
<body>
<script src="libcsound.js"></script>
<script src="FileManager.js"></script>
<script>
Module['noExitRuntime'] = true;
Module['_main'] = function() {
var csoundObj = new CsoundObj();
var fileManger = new FileManager(['csd'], console.log);
fileManger.fileUploadFromServer("test.csd", function() {
csoundObj.compileCSD("test.csd");
});
var startButton = document.createElement("BUTTON");
startButton.innerHTML = "Start Csound";
startButton.onclick = function() {
csoundObj.start();
};
document.body.appendChild(startButton);
};
</script>
</body>
</html>
Here we can see that the button startButton is instantiated using the document.createElement method. The buttons label is set using the innerHTML method, and we can set the buttons action by defining a function and assigning it to the buttons onclick method. The function simply calls the start method from CsoundObj. The button is then added to the DOM using document.body.appendChild.
If the page is reloaded there should now be a button present that is labelled with the text "Start Csound". When the button is pressed csound should perform the .csd file which was uploaded to the javascript file system.
CsoundObj.js Reference
CsoundObj.compileCSD(fileName)
This method takes as its argument the address of a CSD file fileName and compiles it for performance. The CSD file must be present in Emscripten's javascript virtual filesystem.
CsoundObj.disableAudioInput()
This method disables audio input to the web browser. Audio input will not be available to the running Csound instance
CsoundObj.enableAudioInput()
This method enables audio input to the web browser. When called, it triggers a permissions dialogue in the host web browser requesting permission to allow audio input. If permission is granted, audio input is available for the running Csound instance.
CsoundObj.enableMidiInput()
This method enables Midi input to the web browser. When activated on supported browsers (currently only Chrome supports web midi) it is possible for the running instance of Csound to receive midi messages from a compatible input device.
CsoundObj.evaluateCode()
This method takes a string of Csound orchestra code and evaluates it on the fly. Any instruments contained in the code will be created and added to the running Csound process.
CsoundObj.readScore()
This method takes a string of Csound score code and evaluates it.
CsoundObj.render()
This method renders the currently compiled .csd file as quickly as possible. This method is currently only used to evaluate the performance of libcsound.js and is of no practical use to end users.
CsoundObj.reset()
This method resets the currently running instance of Csound. This method should be called before a new .csd file needs to be read and compiled for performance.
CsoundObj.setControlChannel()
This method sets a named Csound control channel to a specified value.
CsoundObj.setControlChannel()
This method gets the current value of a named Csound control channel.
CsoundObj.start()
This method starts a performance of a compiled .csd file.
11 CSOUND UTILITIES
CSOUND UTILITIES
Csound comes bundled with a variety of additional utility applications. These are small programs that perform a single function, very often with a sound file, that might be useful just before or just after working with the main Csound program. Originally these were programs that were run from the command line but many of Csound front-ends now offer direct access to many of these utilities through their own utilities menus. It is useful to still have access to these programs via the command line though, if all else fails.
The standard syntax for using these programs from the command line is to type the name of the utility followed optionally by one or more command line flags which control various performance options of the program - all of these will have useable defaults anyway - and finally the name of the sound file upon which the utility will operate.
utility_name [flag(s)] [file_name(s)]
If we require some help or information about a utility and don't want to be bothered hunting through the Csound Manual we can just type the the utility's name with no additional arguments, hit enter and the commmand line response will give us some information about that utility and what command line flags it offers. We can also run the utility through Csound - perhaps useful if there are problems running the utility directly - by calling Csound with the -U flag. The -U flag will instruct Csound to run the utility and to interpret subsequent flags as those of the utility and not its own.
Csound -U utility_name [flag(s)] [file_name(s)]
sndinfo
As an example of invoking one of these utilities from the command line we shall look at the utility 'sndinfo' (sound information) which provides the user with some information about one or more sound files. 'sndinfo' is invoked and provided with a file name:
sndinfo /Users/iainmccurdy/sounds/mysound.wav
If you are unsure of the file address of your sound file you can always just drag and drop it into the terminal window. The output should be something like:
util sndinfo: /Users/iainmccurdy/sounds/mysound.wav: srate 44100, stereo, 24 bit WAV, 3.335 seconds (147078 sample frames)
'sndinfo' will accept a list of file names and provide information on all of them in one go so it may prove more efficient gleaning the same information from a GUI based sample editor. We also have the advantage of being able to copy and paste from the terminal window into a .csd file.
Analysis Utilities
Although many of Csound's opcodes already operate upon commonly encountered sound file formats such as 'wav' and 'aiff', a number of them require sound information in more specialised and pre-analysed formats, and for this Csound provides the sound analysis utilities atsa, cvanal, hetro, lpanal and pvanal. By far the most commonly used of these is pvanal which, although originally written to provide analysis files for pvoc and its generation of opcodes, has now been extended to be able to generate files in the pvoc-ex (.pvx) format for use with the newer 'pvs' streaming pvoc opcodes.
This time as well as requiring an input sound file for analysis we will need to provide a name (and optionally the full address) for the output file. Using pvanal's command flags we can have full control over typical FFT conversion parameters such as FFT size, overlap, window type etc. as well as additional options that may prove useful such as the ability to select a fragment of a larger sound file for the analysis. In the following illustration we shall make use of just one flag, -s, for selecting which channel of the input sound file to analyse, all other flag values shall assume their default values which should work fine in most situations.
pvanal -s1 mysound.wav myanalysis.pvx
pvanal will analyse the first (left if stereo) channel of the input sound file 'mysound.wav' (and in this case as no full address has been provided it will need to be in either the current working directory or SSDIR), and a name has been provided for the output file 'myanalysis.pvx', which, as no full address has been given, will be placed in the current working directory. While pvanal is running it will print a running momentary and finally inform us once the process is complete.
If you use CsoundQT you can have direct access to pvanal with all its options through the 'utilities' button in the toolbar. Once opened it will reveal a dialogue window looking something like this:
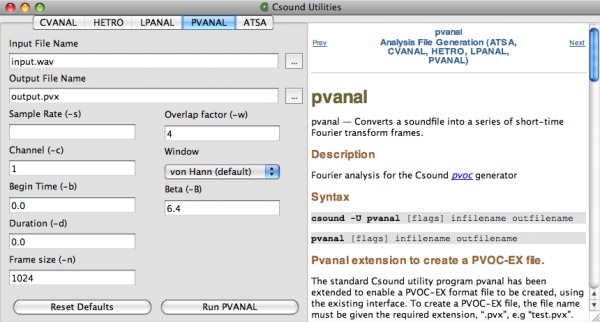
Especially helpful is the fact that we are also automatically provided with pvanal's manual page.
File Conversion Utilities
The next group of utilities, het_import, het_export, pvlook, pv_export, pv_import, sdif2ad and srconv facilitate file conversions between various types. Perhaps the most interesting of these are pvlook, which prints to the terminal a formatted text version of a pvanal file - useful to finding out exactly what is going on inside individual analysis bins, something that may be of use when working with the more advanced resynthesis opcodes such as pvadd or pvsbin. srconv can be used to convert the sample rate of a sound file.
Miscellaneous Utilities
A final group gathers together various unsorted utilities: cs, csb64enc, envext, extractor, makecsd, mixer, scale and mkdb. Most interesting of these are perhaps extractor which will extract a user defined fragment of a sound file which it will then write to a new file, mixer which mixes together any number of sound files and with gain control over each file and scale which will scale the amplitude of an individual sound file.
Conclusion
It has been seen that the Csound utilities offer a wealth of useful, but often overlooked, tools to augment our work with Csound. Whilst some of these utilities may seem redundant now that most of us have access to fully featured 3rd-party sound editing software, it should be borne in mind that many of these utilities were written in the 1980s and early 90s when such tools were less readily available.
12 CSOUND AND OTHER PROGRAMMING LANGUAGES
THE CSOUND API
An application programming interface (API) is an interface provided by a computer system, library or application that allows users to access functions and routines for a particular task. It gives developers a way to harness the functionality of existing software within a host application. The Csound API can be used to control an instance of Csound through a series of different functions thus making it possible to harness all the power of Csound in one’s own applications. In other words, almost anything that can be done within Csound can be done with the API. The API is written in C, but there are interfaces to other languages as well, such as Python, C++ and Java.Though it is written in C, the Csound API uses an object structure. This is achieved through an opaque pointer representing a Csound instance. This opaque pointer is passed as the first argument when an API function is called from the host program.
To use the Csound C API, you have to include csound.h in your source file and to link your code with libcsound64 (or libcsound if using the 32 bit version of the library). Here is an example of the csound command line application written in C, using the Csound C API:
#include <csound/csound.h>
int main(int argc, char **argv)
{
CSOUND *csound = csoundCreate(NULL);
int result = csoundCompile(csound, argc, argv);
if (result == 0) {
result = csoundPerform(csound);
}
csoundDestroy(csound);
return (result >= 0 ? 0 : result);
}
First we create an instance of Csound. To do this we call csoundCreate() which returns the opaque pointer that will be passed to most Csound API functions. Then we compile the orc/sco files or the csd file given as input arguments through the argv parameter of the main function. If the compilation is successful (result == 0), we call the csoundPerform() function. csoundPerform() will cause Csound to perform until the end of the score is reached. When this happens csoundPerform() returns a non-zero value and we destroy our instance before ending the program.
On a linux system, using libcsound64 (double version of the csound library), supposing that all include and library paths are set correctly, we would build the above example with the following command (notice the use of the -DUSE_DOUBLE flag to signify that we compile against the 64 bit version of the csound library):
gcc -DUSE_DOUBLE -o csoundCommand csoundCommand.c -lcsound64
The command for building with a 32 bit version of the library would be:
gcc -o csoundCommand csoundCommand.c -lcsound
Within the C or C++ examples of this chapter, we will use the MYFLT type for the audio samples. Doing so, the same source files can be used for both development (32 bit or 64 bit), the compiler knowing how to interpret MYFLT as double if the macro USE_DOUBLE is defined, or as float if the macro is not defined.
The C API has been wrapped in a C++ class for convenience. This gives the Csound basic C++ API. With this API, the above example would become:
#include <csound/csound.hpp>
int main(int argc, char **argv)
{
Csound *cs = new Csound();
int result = cs->Compile(argc, argv);
if (result == 0) {
result = cs->Perform();
}
return (result >= 0 ? 0 : result);
}
Here, we get a pointer to a Csound object instead of the csound opaque pointer. We call methods of this object instead of C functions, and we don't need to call csoundDestroy in the end of the program, because the C++ object destruction mechanism takes care of this. On our linux system, the example would be built with the following command:
g++ -DUSE_DOUBLE -o csoundCommandCpp csoundCommand.cpp -lcsound64
Threading
Before we begin to look at how to control Csound in real time we need to look at threads. Threads are used so that a program can split itself into two or more simultaneously running tasks. Multiple threads can be executed in parallel on many computer systems. The advantage of running threads is that you do not have to wait for one part of your software to finish executing before you start another.
In order to control aspects of your instruments in real time your will need to employ the use of threads. If you run the first example found on this page you will see that the host will run for as long as csoundPerform() returns 0. As soon as it returns non-zero it will exit the loop and cause the application to quit. Once called, csoundPerform() will cause the program to hang until it is finished. In order to interact with Csound while it is performing you will need to call csoundPerform() in a separate unique thread.
When implementing threads using the Csound API, we must define a special performance function thread. We then pass the name of this performance function to csoundCreateThread(), thus registering our performance-thread function with Csound. When defining a Csound performance-thread routine you must declare it to have a return type uintptr_t, hence it will need to return a value when called. The thread function will take only one parameter, a pointer to void. This pointer to void is quite important as it allows us to pass important data from the main thread to the performance thread. As several variables are needed in our thread function the best approach is to create a user defined data structure that will hold all the information your performance thread will need. For example:
typedef struct {
int result; /* result of csoundCompile() */
CSOUND *csound; /* instance of csound */
bool PERF_STATUS; /* performance status */
} userData;
Below is a basic performance-thread routine. *data is cast as a userData data type so that we can access its members.
uintptr_t csThread(void *data)
{
userData *udata = (userData *)data;
if (!udata->result) {
while ((csoundPerformKsmps(udata->csound) == 0) &&
(udata->PERF_STATUS == 1));
csoundDestroy(udata->csound);
}
udata->PERF_STATUS = 0;
return 1;
}
In order to start this thread we must call the csoundCreateThread() API function which is declared in csound.h as:
void *csoundCreateThread(uintptr_t (*threadRoutine (void *),
void *userdata);
If you are building a command line program you will need to use some kind of mechanism to prevent int main() from returning until after the performance has taken place. A simple while loop will suffice.
The first example presented above can now be rewritten to include a unique performance thread:
#include <stdio.h>
#include <csound/csound.h>
uintptr_t csThread(void *clientData);
typedef struct {
int result;
CSOUND *csound;
int PERF_STATUS;
} userData;
int main(int argc, char *argv[])
{
int finish;
void *ThreadID;
userData *ud;
ud = (userData *)malloc(sizeof(userData));
MYFLT *pvalue;
ud->csound = csoundCreate(NULL);
ud->result = csoundCompile(ud->csound, argc, argv);
if (!ud->result) {
ud->PERF_STATUS = 1;
ThreadID = csoundCreateThread(csThread, (void *)ud);
}
else {
return 1;
}
/* keep performing until user types a number and presses enter */
scanf("%d", &finish);
ud->PERF_STATUS = 0;
csoundDestroy(ud->csound);
free(ud);
return 0;
}
/* performance thread function */
uintptr_t csThread(void *data)
{
userData *udata = (userData *)data;
if (!udata->result) {
while ((csoundPerformKsmps(udata->csound) == 0) &&
(udata->PERF_STATUS == 1));
csoundDestroy(udata->csound);
}
udata->PERF_STATUS = 0;
return 1;
}
The application above might not appear all that interesting. In fact it's almost the exact same as the first example presented except that users can now stop Csound by hitting 'enter'. The real worth of threads can only be appreciated when you start to control your instrument in real time.
Channel I/O
The big advantage to using the API is that it allows a host to control your Csound instruments in real time. There are several mechanisms provided by the API that allow us to do this. The simplest mechanism makes use of a 'software bus'.
The term bus is usually used to describe a means of communication between hardware components. Buses are used in mixing consoles to route signals out of the mixing desk into external devices. Signals get sent through the sends and are taken back into the console through the returns. The same thing happens in a software bus, only instead of sending analog signals to different hardware devices we send data to and from different software.
Using one of the software bus opcodes in Csound we can provide an interface for communication with a host application. An example of one such opcode is chnget. The chnget opcode reads data that is being sent from a host Csound API application on a particular named channel, and assigns it to an output variable. In the following example instrument 1 retrieves any data the host may be sending on a channel named "pitch":
instr 1
kfreq chnget "pitch"
asig oscil 10000, kfreq, 1
out asig
endin
One way in which data can be sent from a host application to an instance of Csound is through the use of the csoundGetChannelPtr() API function which is defined in csound.h as:
int csoundGetChannelPtr(CSOUND *, MYFLT **p, const char *name, int type);
CsoundGetChannelPtr() stores a pointer to the specified channel of the bus in p. The channel pointer p is of type MYFLT *. The argument name is the name of the channel and the argument type is a bitwise OR of exactly one of the following values:
CSOUND_CONTROL_CHANNEL - control data (one MYFLT value)
CSOUND_AUDIO_CHANNEL - audio data (ksmps MYFLT values)
CSOUND_STRING_CHANNEL - string data (MYFLT values with enough space to store csoundGetChannelDatasize() characters, including the NULL character at the end of the string)
and at least one of these:
CSOUND_INPUT_CHANNEL - when you need Csound to accept incoming values from a host
CSOUND_OUTPUT_CHANNEL - when you need Csound to send outgoing values to a host
If the call to csoundGetChannelPtr() is successful the function will return zero. If not, it will return a negative error code. We can now modify our previous code in order to send data from our application on a named software bus to an instance of Csound using csoundGetChannelPtr().
#include <stdio.h>
#include <csound/csound.h>
/* performance thread function prototype */
uintptr_t csThread(void *clientData);
/* userData structure declaration */
typedef struct {
int result;
CSOUND *csound;
int PERF_STATUS;
} userData;
/*-----------------------------------------------------------
* main function
*-----------------------------------------------------------*/
int main(int argc, char *argv[])
{
int userInput = 200;
void *ThreadID;
userData *ud;
ud = (userData *)malloc(sizeof(userData));
MYFLT *pvalue;
ud->csound = csoundCreate(NULL);
ud->result = csoundCompile(ud->csound, argc, argv);
if (csoundGetChannelPtr(ud->csound, &pvalue, "pitch",
CSOUND_INPUT_CHANNEL | CSOUND_CONTROL_CHANNEL) != 0) {
printf("csoundGetChannelPtr could not get the \"pitch\" channel");
return 1;
}
if (!ud->result) {
ud->PERF_STATUS = 1;
ThreadID = csoundCreateThread(csThread, (void*)ud);
}
else {
printf("csoundCompiled returned an error");
return 1;
}
printf("\nEnter a pitch in Hz(0 to Exit) and type return\n");
while (userInput != 0) {
*pvalue = (MYFLT)userInput;
scanf("%d", &userInput);
}
ud->PERF_STATUS = 0;
csoundDestroy(ud->csound);
free(ud);
return 0;
}
/*-----------------------------------------------------------
* definition of our performance thread function
*-----------------------------------------------------------*/
uintptr_t csThread(void *data)
{
userData *udata = (userData *)data;
if (!udata->result) {
while ((csoundPerformKsmps(udata->csound) == 0) &&
(udata->PERF_STATUS == 1));
csoundDestroy(udata->csound);
}
udata->PERF_STATUS = 0;
return 1;
}
There are several ways of sending data to and from Csound through software buses. They are divided in two categories:
Named Channels with no Callback
This category uses csoundGetChannelPtr() to get a pointer to the data of the named channel. There are also six functions to send data to and from a named channel in a thread safe way:
| MYFLT csoundGetControlChannel(CSOUND *csound, const char *name, int *err)
|
| void csoundSetControlChannel(CSOUND *csound, const char *name, MYFLT val)
|
| void csoundGetAudioChannel(CSOUND *csound, const char *name, MYFLT *samples)
|
| void csoundSetAudioChannel(CSOUND *csound, const char *name, MYFLT *samples)
|
| void csoundGetStringChannel(CSOUND *csound, const char *name, char *string)
|
| void csoundSetStringChannel(CSOUND *csound, const char *name, char *string)
|
The opcodes concerned are chani, chano, chnget and chnset. When using numbered channels with chani and chano, the API sees those channels as named channels, the name being derived from the channel number (i.e. 1 gives "1", 17 gives "17", etc).
There is also a helper function returning the data size of a named channel:
int csoundGetChannelDatasize(CSOUND *csound, const char *name)
It is particularly useful when dealing with string channels.
Named Channels with Callback
Each time a named channel with callback is used (opcodes invalue, outvalue, chnrecv, and chnsend), the corresponding callback registered by one of those functions will be called:
| void csoundSetInputChannelCallback(CSOUND *csound,
|
| channelCallback_t inputChannelCalback)
|
| void csoundSetOutputChannelCallback(CSOUND *csound, |
| channelCallback_t outputChannelCalback)
|
Other Channel Functions
| int csoundSetPvsChannel(CSOUND *, const PVSDATEXT *fin, const char *name), and
|
| int csoundGetPvsChannel(CSOUND *csound, PVSDATEXT *fout, const char *name)
|
| int csoundSetControlChannelHints(CSOUND *, const char *name, |
| controlChannelHints_t hints), and
|
| int csoundGetControlChannelHints(CSOUND *, const char *name, |
| controlChannelHints_t *hints)
|
int *csoundGetChannelLock(CSOUND *, const char *name)
| int csoundKillInstance(CSOUND *csound, MYFLT instr,
|
| char *instrName, int mode, int allow_release)
|
kills off one or more running instances of an instrument.
| int csoundRegisterKeyboardCallback(CSOUND *,
|
| int (*func)(void *userData, void *p, unsigned int type),
|
| void *userData, unsigned int type), and
|
| void csoundRemoveKeyboardCallback(CSOUND *csound,
|
| int (*func)(void *, void *, unsigned int))
|
Score Events
Adding score events to the csound instance is easy to do. It requires that csound has its threading done, see the paragraph above on threading. To enter a score event into csound, one calls the following function:
void myInputMessageFunction(void *data, const char *message)
{
userData *udata = (userData *)data;
csoundInputMessage(udata->csound, message );
}
Now we can call that function to insert Score events into a running csound instance. The formatting of the message should be the same as one would normally have in the Score part of the .csd file. The example shows the format for the message. Note that if you're allowing csound to print its error messages, if you send a malformed message, it will warn you. Good for debugging. There's an example with the csound source code that allows you to type in a message, and then it will send it.
/* instrNum start duration p4 p5 p6 ... pN */ const char *message = "i1 0 1 0.5 0.3 0.1"; myInputMessageFunction((void*)udata, message);
Callbacks
Csound can call subroutines declared in the host program when some special events occur. This is done through the callback mechanism. One has to declare to Csound the existence of a callback routine using an API setter function. Then when a corresponding event occurs during performance, Csound will call the host callback routine, eventually passing some arguments to it.
The example below shows a very simple command line application allowing the user to rewind the score or to abort the performance. This is achieved by reading characters from the keyboard: 'r' for rewind and 'q' for quit. During performance, Csound executes a loop. Each pass in the loop yields ksmps audio frames. Using the API csoundSetYieldCallback function, we can tell to Csound to call our own routine after each pass in its internal loop.
The yieldCallback routine must be non-blocking. That's why it is a bit tricky to force the C getc function to be non-blocking. To enter a character, you have to type the character and then hit the return key.
#include <csound/csound.h>
int yieldCallback(CSOUND *csound)
{
int fd, oldstat, dummy;
char ch;
fd = fileno(stdin);
oldstat = fcntl(fd, F_GETFL, dummy);
fcntl(fd, F_SETFL, oldstat | O_NDELAY);
ch = getc(stdin);
fcntl(fd, F_SETFL, oldstat);
if (ch == -1)
return 1;
switch (ch) {
case 'r':
csoundRewindScore(csound);
break;
case 'q':
csoundStop(csound);
break;
}
return 1;
}
int main(int argc, char **argv)
{
CSOUND *csound = csoundCreate(NULL);
csoundSetYieldCallback(csound, yieldCallback);
int result = csoundCompile(csound, argc, argv);
if (result == 0) {
result = csoundPerform(csound);
}
csoundDestroy(csound);
return (result >= 0 ? 0 : result);
}
The user can also set callback routines for file open events, real-time audio events, real-time MIDI events, message events, keyboards events, graph events, and channel invalue and outvalue events.
CsoundPerformanceThread: a Swiss Knife for the API
Beside the API, Csound provides a helper C++ class to facilitate threading issues: CsoundPerformanceThread. This class performs a score in a separate thread, allowing the host program to do its own processing in its main thread during the score performance. The host program will communicate with the CsoundPerformanceThread class by sending messages to it, calling CsoundPerformanceThread methods. Those messages are queued inside CsoundPerformanceThread and are treated in a first in first out (FIFO) manner.
The example below is equivalent to the example in the callback section. But this time, as the characters are read in a different thread, there is no need to have a non-blocking character reading routine.
#include <csound/csound.hpp>
#include <csound/csPerfThread.hpp>
#include <iostream>
using namespace std;
int main(int argc, char **argv)
{
Csound *cs = new Csound();
int result = cs->Compile(argc, argv);
if (result == 0) {
CsoundPerformanceThread *pt = new CsoundPerformanceThread(cs);
pt->Play();
while (pt->GetStatus() == 0) {
char c = cin.get();
switch (c) {
case 'r':
cs->RewindScore();
break;
case 'q':
pt->Stop();
pt->Join();
break;
}
}
}
return (result >= 0 ? 0 : result);
}
Because CsoundPerformanceThread is not part of the API, we have to link to libcsnd6 to get it working:
g++ -DUSE_DOUBLE -o perfThread perfThread.cpp -lcsound64 -lcsnd6
When using this class from Python or Java, this is not an issue because the csnd6.py module and the csnd6.jar package include the API functions and classes, and the CsoundPerformanceThread class as well (see below).
Here is a more complete example which could be the base of a frontal application to run Csound. The host application is modeled through the CsoundSession class which has its own event loop (mainLoop). CsoundSession inherits from the API Csound class and it embeds an object of type CsoundPerformanceThread. Most of the CsoundPerformanceThread class methods are used.
#include <csound/csound.hpp>
#include <csound/csPerfThread.hpp>
#include <iostream>
#include <string>
using namespace std;
class CsoundSession : public Csound
{
public:
CsoundSession(string const &csdFileName = "") : Csound() {
m_pt = NULL;
m_csd = "";
if (!csdFileName.empty()) {
m_csd = csdFileName;
startThread();
}
};
void startThread() {
if (Compile((char *)m_csd.c_str()) == 0 ) {
m_pt = new CsoundPerformanceThread(this);
m_pt->Play();
}
};
void resetSession(string const &csdFileName) {
if (!csdFileName.empty())
m_csd = csdFileName;
if (!m_csd.empty()) {
stopPerformance();
startThread();
}
};
void stopPerformance() {
if (m_pt) {
if (m_pt->GetStatus() == 0)
m_pt->Stop();
m_pt->Join();
m_pt = NULL;
}
Reset();
};
void mainLoop() {
string s;
bool loop = true;
while (loop) {
cout << endl << "l)oad csd; e(vent; r(ewind; t(oggle pause; s(top; p(lay; q(uit: ";
char c = cin.get();
switch (c) {
case 'l':
cout << "Enter the name of csd file:";
cin >> s;
resetSession(s);
break;
case 'e':
cout << "Enter a score event:";
cin.ignore(1000, '\n'); //a bit tricky, but well, this is C++!
getline(cin, s);
m_pt->InputMessage(s.c_str());
break;
case 'r':
RewindScore();
break;
case 't':
if (m_pt)
m_pt->TogglePause();
break;
case 's':
stopPerformance();
break;
case 'p':
resetSession("");
break;
case 'q':
if (m_pt) {
m_pt->Stop();
m_pt->Join();
}
loop = false;
break;
}
cout << endl;
}
};
private:
string m_csd;
CsoundPerformanceThread *m_pt;
};
int main(int argc, char **argv)
{
string csdName = "";
if (argc > 1)
csdName = argv[1];
CsoundSession *session = new CsoundSession(csdName);
session->mainLoop();
}
The application is built with the following command:
g++ -o csoundSession csoundSession.cpp -lcsound64 -lcsnd6When using this class from Python or Java, this is not an issue because the csnd6.py module
There are also methods in CsoundPerformanceThread for sending score events (ScoreEvent), for moving the time pointer (SetScoreOffsetSeconds), for setting a callback function (SetProcessCallback) to be called at the end of each pass in the process loop, and for flushing the message queue (FlushMessageQueue).
As an exercise, the user should complete this example using the methods above and then try to rewrite the example in Python and/or in Java (see below).
Csound API Review
The best source of information is the csound.h header file. Let us review some important API functions in a C++ example:
#include <csound/csound.hpp>
#include <csound/csPerfThread.hpp>
#include <iostream>
#include <string>
#include <vector>
using namespace std;
string orc1 =
"instr 1 \n"
"idur = p3 \n"
"iamp = p4 \n"
"ipch = cpspch(p5) \n"
"kenv linen iamp, 0.05, idur, 0.1 \n"
"a1 poscil kenv, ipch \n"
" out a1 \n"
"endin";
string orc2 =
"instr 1 \n"
"idur = p3 \n"
"iamp = p4 \n"
"ipch = cpspch(p5) \n"
"a1 foscili iamp, ipch, 1, 1.5, 1.25 \n"
" out a1 \n"
"endin\n";
string orc3 =
"instr 1 \n"
"idur = p3 \n"
"iamp = p4 \n"
"ipch = cpspch(p5-1) \n"
"kenv linen iamp, 0.05, idur, 0.1 \n"
"asig rand 0.45 \n"
"afilt moogvcf2 asig, ipch*4, ipch/(ipch * 1.085) \n"
"asig balance afilt, asig \n"
" out kenv*asig \n"
"endin\n";
string sco1 =
"i 1 0 1 0.5 8.00\n"
"i 1 + 1 0.5 8.04\n"
"i 1 + 1.5 0.5 8.07\n"
"i 1 + 0.25 0.5 8.09\n"
"i 1 + 0.25 0.5 8.11\n"
"i 1 + 0.5 0.8 9.00\n";
string sco2 =
"i 1 0 1 0.5 9.00\n"
"i 1 + 1 0.5 8.07\n"
"i 1 + 1 0.5 8.04\n"
"i 1 + 1 0.5 8.02\n"
"i 1 + 1 0.5 8.00\n";
string sco3 =
"i 1 0 0.5 0.5 8.00\n"
"i 1 + 0.5 0.5 8.04\n"
"i 1 + 0.5 0.5 8.00\n"
"i 1 + 0.5 0.5 8.04\n"
"i 1 + 0.5 0.5 8.00\n"
"i 1 + 0.5 0.5 8.04\n"
"i 1 + 1.0 0.8 8.00\n";
void noMessageCallback(CSOUND* cs, int attr, const char *format, va_list valist)
{
// Do nothing so that Csound will not print any message,
// leaving a clean console for our app
return;
}
class CsoundSession : public Csound
{
public:
CsoundSession(vector<string> & orc, vector<string> & sco) : Csound() {
m_orc = orc;
m_sco = sco;
m_pt = NULL;
};
void mainLoop() {
SetMessageCallback(noMessageCallback);
SetOutput((char *)"dac", NULL, NULL);
GetParams(&m_csParams);
m_csParams.sample_rate_override = 48000;
m_csParams.control_rate_override = 480;
m_csParams.e0dbfs_override = 1.0;
// Note that setParams is called before first compilation
SetParams(&m_csParams);
if (CompileOrc(orc1.c_str()) == 0) {
Start(this->GetCsound());
// Just to be sure...
cout << GetSr() << ", " << GetKr() << ", ";
cout << GetNchnls() << ", " << Get0dBFS() << endl;
m_pt = new CsoundPerformanceThread(this);
m_pt->Play();
}
else {
return;
}
string s;
TREE *tree;
bool loop = true;
while (loop) {
cout << endl << "1) 2) 3): orchestras, 4) 5) 6): scores; q(uit: ";
char c = cin.get();
cin.ignore(1, '\n');
switch (c) {
case '1':
tree = ParseOrc(m_orc[0].c_str());
CompileTree(tree);
DeleteTree(tree);
break;
case '2':
CompileOrc(m_orc[1].c_str());
break;
case '3':
EvalCode(m_orc[2].c_str());
break;
case '4':
ReadScore((char *)m_sco[0].c_str());
break;
case '5':
ReadScore((char *)m_sco[1].c_str());
break;
case '6':
ReadScore((char *)m_sco[2].c_str());
break;
case 'q':
if (m_pt) {
m_pt->Stop();
m_pt->Join();
}
loop = false;
break;
}
}
};
private:
CsoundPerformanceThread *m_pt;
CSOUND_PARAMS m_csParams;
vector<string> m_orc;
vector<string> m_sco;
};
int main(int argc, char **argv)
{
vector<string> orc;
orc.push_back(orc1);
orc.push_back(orc2);
orc.push_back(orc3);
vector<string> sco;
sco.push_back(sco1);
sco.push_back(sco2);
sco.push_back(sco3);
CsoundSession *session = new CsoundSession(orc, sco);
session->mainLoop();
}
Deprecated Functions
csoundQueryInterface(), csoundSetInputValueCallback(), csoundSetOutputValueCallback(), csoundSetChannelIOCallback(), and csoundPerformKsmpsAbsolute() are still in the header file but are now deprecated.
Builtin Wrappers
The Csound API has also been wrapped to other languages. Usually Csound is built and distributed including a wrapper for Python and a wrapper for Java. Those wrappers are automatically generated using the SWIG development tool.
To use the Python Csound API wrapper, you have to import the csnd6 module. The csnd6 module is normally installed in the site-packages or dist-packages directory of your python distribution as a csnd6.py file. Our csound command example becomes:
import sys
import csnd6
def csoundCommand(args):
csound = csnd6.Csound()
arguments = csnd6.CsoundArgVList()
for s in args:
arguments.Append(s)
result = csound.Compile(arguments.argc(), arguments.argv())
if result == 0:
result = csound.Perform()
return result
def main():
csoundCommand(sys.argv)
if __name__ =='__main__':
main()
We use a Csound object (remember Python has OOp features). Note the use of the CsoundArgVList helper class to wrap the program input arguments into a C++ manageable object. In fact, the Csound class has syntactic sugar (thanks to method overloading) for the Compile method. If you have less than six string arguments to pass to this method, you can pass them directly. But here, as we don't know the number of arguments to our csound command, we use the more general mechanism of the CsoundArgVList helper class.
This example would be launched with the following command:
python csoundCommand.py myexample.csd
To use the Java Csound API wrapper, you have to import the csnd6 package. The csnd6 package is located in the csnd6.jar archive which has to be known from your Java path. Our csound command example becomes:
import csnd6.*;
public class CsoundCommand
{
private Csound csound = null;
private CsoundArgVList arguments = null;
public CsoundCommand(String[] args) {
csound = new Csound();
arguments = new CsoundArgVList();
arguments.Append("dummy");
for (int i = 0; i < args.length; i++) {
arguments.Append(args[i]);
}
int result = csound.Compile(arguments.argc(), arguments.argv());
if (result == 0) {
result = csound.Perform();
}
System.out.println(result);
}
public static void main(String[] args) {
CsoundCommand csCmd = new CsoundCommand(args);
}
}
Note the "dummy" string as first argument in the arguments list. C, C++ and Python expect that the first argument in a program argv input array is implicitly the name of the calling program. This is not the case in Java: the first location in the program argv input array contains the first command line argument if any. So we have to had this "dummy" string value in the first location of the arguments array so that the C API function called by our csound.Compile method is happy.
This illustrates a fundamental point about the Csound API. Whichever API wrapper is used (C++, Python, Java, etc), it is the C API which is working under the hood. So a thorough knowledge of the Csound C API is highly recommended if you plan to use the Csound API in any of its different flavours.On our linux system, with csnd.jar located in /usr/local/lib/, our Java Program would be compiled and run with the following commands:
javac -cp /usr/local/lib/csnd6.jar CsoundCommand.java java -cp /usr/local/lib/csnd6.jar:. CsoundCommand
There is a drawback using those wrappers: as they are built during the Csound build, the host system on which Csound will be used must have the same version of Python and Java than the ones which were on the system used to build Csound. The mechanism presented in the next section can solve this problem.
Foreign Function Interfaces
Modern programming languages often propose a mechanism called Foreign Function Interface (FFI) which allows the user to write an interface to shared libraries written in C.
Python provides the ctypes module which can be used for this purpose. Here is a version of the csound command using ctypes:
# This is the wrapper part defining our python interface to
# the Csound API functions that we will use, and a helper function
# called csoundArgList, which makes a pair of C argc, argv arguments from
# a python string list.
# This wrapper could be written in a separate file and imported
# in the main program.
import ctypes as ct
libcsound = ct.CDLL("libcsound64.so")
csoundCreate = libcsound.csoundCreate
csoundCreate.restype = ct.c_void_p
csoundCreate.argtypes = [ct.c_void_p]
csoundCompile = libcsound.csoundCompile
csoundCompile.restype = ct.c_int
csoundCompile.argtypes = [ct.c_void_p, ct.c_int, ct.POINTER(ct.c_char_p)]
csoundPerform = libcsound.csoundPerform
csoundPerform.restype = ct.c_int
csoundPerform.argtypes = [ct.c_void_p]
csoundDestroy = libcsound.csoundDestroy
csoundDestroy.argtype = [ct.c_void_p]
def csoundArgList(lst):
argc = ct.c_int(len(lst))
argv = (ct.POINTER(ct.c_char_p) * len(lst))()
for i in range(len(lst)):
argv[i] = ct.cast(ct.pointer(ct.create_string_buffer(lst[i])), \
ct.POINTER(ct.c_char_p))
return argc, ct.cast(argv, ct.POINTER(ct.c_char_p))
# This is the Csound commandline program using the wrapper interface
import sys
argc, argv = csoundArgList(sys.argv)
csound = csoundCreate(None)
result = csoundCompile(csound, argc, argv)
if result == 0:
csoundPerform(csound)
csoundDestroy(csound)
Lua proposes the same functionality through the LuaJIT project. Here is a version of the csound command using LuaJIT FFI:
-- This is the wrapper part defining our LuaJIT interface to
-- the Csound API functions that we will use, and a helper function
-- called csoundCompile, which makes a pair of C argc, argv arguments from
-- the script input args and calls the API csoundCompile function
-- This wrapper could be written in a separate file and imported
-- in the main program.
local ffi = require("ffi")
ffi.cdef[[
typedef void CSOUND;
CSOUND *csoundCreate(void *hostData);
int csoundCompile(CSOUND *, int argc, const char *argv[]);
int csoundPerform(CSOUND *);
void csoundDestroy(CSOUND *);
]]
csoundAPI = ffi.load("csound64.so")
string_array_t = ffi.typeof("const char *[?]")
function csoundCompile(csound, args)
local argv = {"dummy"}
for i, v in ipairs(args) do
argv[i+1] = v
end
local cargv = string_array_t(#argv + 1, argv)
cargv[#argv] = nil
return csoundAPI.csoundCompile(csound, #argv, cargv)
end
-- This is the Csound commandline program using the wrapper interface
csound = csoundAPI.csoundCreate(nil)
result = csoundCompile(csound, {...})
if result == 0 then
csoundAPI.csoundPerform(csound)
end
csoundAPI.csoundDestroy(csound)
The FFI package of the Google Go programming language is called cgo. Here is a version of the csound command using cgo:
package main
/* This is the wrapper part defining our Go interface to
the Csound API functions that we will use. It uses the go object
model building methods that will call the corresponding API functions.
This wrapper could be written in a separate file and imported
in the main program.
*/
/*
#cgo CFLAGS: -DUSE_DOUBLE=1
#cgo CFLAGS: -I /usr/local/include
#cgo linux CFLAGS: -DLINUX=1
#cgo LDFLAGS: -lcsound64
#include <csound/csound.h>
*/
import "C"
import (
"os"
"unsafe"
)
type CSOUND struct {
Cs (*C.CSOUND)
}
type MYFLT float64
func CsoundCreate(hostData unsafe.Pointer) CSOUND {
var cs (*C.CSOUND)
if hostData != nil {
cs = C.csoundCreate(hostData)
} else {
cs = C.csoundCreate(nil)
}
return CSOUND{cs}
}
func (csound CSOUND) Compile(args []string) int {
argc := C.int(len(args))
argv := make([]*C.char, argc)
for i, arg := range args {
argv[i] = C.CString(arg)
}
result := C.csoundCompile(csound.Cs, argc, &argv[0])
for _, arg := range argv {
C.free(unsafe.Pointer(arg))
}
return int(result)
}
func (csound CSOUND) Perform() int {
return int(C.csoundPerform(csound.Cs))
}
func (csound *CSOUND) Destroy() {
C.csoundDestroy(csound.Cs)
csound.Cs = nil
}
// This is the Csound commandline program using the wrapper interface
func main() {
csound := CsoundCreate(nil)
if result := csound.Compile(os.Args); result == 0 {
csound.Perform()
}
csound.Destroy()
}
A complete wrapper to the Csound API written in Go is available at https://github.com/fggp/go-csnd6.
The different examples in this section are written for Linux. For other operating systems, some adaptations are needed: for example, for Windows the library name suffix is .dll instead of .so.
The advantage of FFI over Builtin Wrappers is that as long as the signatures of the functions in the interface are the same than the ones in the API, it will work without caring about the version number of the foreign programming language used to write the host program. Moreover, one need to include in the interface only the functions used in the host program. However a good understanding of the C language low level features is needed to write the helper functions needed to adapt the foreign language data structures to the C pointer system.
References & Links
Rory Walsh 2006, "Developing standalone applications using the Csound Host API and wxWidgets", Csound Journal Volume 1 Issue 4 - Summer 2006, http://csoundjournal.com/2006summer/wxCsound.html
Rory Walsh 2010, "Developing Audio Software with the Csound Host API", The Audio Programming Book, DVD Chapter 35, The MIT Press
François Pinot 2011, "Real-time Coding Using the Python API: Score Events", Csound Journal Issue 14 - Winter 2011, http://csoundjournal.com/issue14/realtimeCsoundPython.html
François Pinot 2014, "Go Binding for Csound6", https://github.com/fggp/go-csnd6
Note: A collection of examples in different languages can be found at http://github.com/csound/csoundAPI_examples.
PYTHON INSIDE CSOUND
This chapter is based on Andrés Cabrera's article Using Python inside Csound, An introduction to the Python opcodes, Csound Journal Issue 6, Spring 2007: http://csoundjournal.com/issue6/pythonOpcodes.html. Some basic knowledge of Python is required. For using Csound's Python opcodes, you must have Python installed (currently version 2.7, Python 3.x will not work). This should be the case on OSX1 and Linux. For Windows some version of Python 2.7 must be installed. If you're using 64-bit Csound, you must install a 64-bit version of Python 2.7. Python 2.7.8 for Windows is the most recent 64-bit version of 2.7. This can be downloaded from https://www.python.org/download/releases/2.7.8. When running the Windows Csound installer, you must also check the "Python features" checkbox in the Select Components dialog.
Starting the Python Interpreter and Running Python Code at i-Time: pyinit and pyruni
To use the Python opcodes inside Csound, you must first start the Python interpreter. This is done using the pyinit opcode. The pyinit opcode must be put in the header before any other Python opcode is used, otherwise, since the interpreter is not running, all Python opcodes will return an error. You can run any Python code by placing it within quotes as argument to the opcode pyruni. This opcode executes the Python code at init time and can be put in the heade. The example below, shows a simple csd file which prints the text "Hello Csound world!" to the terminal.2 Note that a dummy instrument must be declared to satisfy the Csound parser.
EXAMPLE 12B01_pyinit.csd
<CsoundSynthesizer> <CsOptions> -ndm0 </CsOptions> <CsInstruments> ;start python interpreter pyinit ;run python code at init-time pyruni "print '*********************'" pyruni "print '*Hello Csound world!*'" pyruni "print '*********************'" instr 1 endin </CsInstruments> <CsScore> i 1 0 0 </CsScore> </CsoundSynthesizer> ;Example by Andrés Cabrera and Joachim Heintz
Prints:
*********************
*Hello Csound world!*
*********************
Python Variables Are Usually Global
The Python interpreter maintains its state for the length of the Csound run. This means that any variables declared will be available on all calls to the Python interpreter. In other words, they are global. The code below shows variables "c" and "d" being calculated both in the header ("c") and in instrument 2 ("d"), and that they are available in all instruments (here printed out in instrument 1 and 3). A multi-line string can be written in Csound with the {{...}} delimiters. This can be useful for longer Python code snippets.
EXAMPLE 12B02_python_global.csd
<CsoundSynthesizer>
<CsOptions>
-ndm0
</CsOptions>
<CsInstruments>
pyinit
;Execute a python script in the header
pyruni {{
a = 2
b = 3
c = a + b
}}
instr 1 ;print the value of c
prints "Instrument %d reports:\n", p1
pyruni "print 'a + b = c = %d' % c"
endin
instr 2 ;calculate d
prints "Instrument %d calculates the value of d!\n", p1
pyruni "d = c**2"
endin
instr 3 ;print the value of d
prints "Instrument %d reports:\n", p1
pyruni "print 'c squared = d = %d' % d"
endin
</CsInstruments>
<CsScore>
i 1 1 0
i 2 3 0
i 3 5 0
</CsScore>
</CsoundSynthesizer>
;Example by Andrés Cabrera and Joachim Heintz
Prints:
Instrument 1 reports:
a + b = c = 5
Instrument 2 calculates the value of d!
Instrument 3 reports:
c squared = d = 25
Running Python Code at k-Time
Python scripts can also be executed at k-rate using pyrun. When pyrun is used, the script will be executed again on every k-pass for the instrument, which means it will be executed kr times per second. The example below shows a simple example of pyrun. The number of control cycles per second is set here to 100 via the statement kr=100. After setting the value of variable "a" in the header to zero, instrument 1 runs for one second, thus incrementing the value of "a" to 100 by the Python statement a = a + 1. Instrument 2, starting after the first second, prints the value. Instrument 1 is then called again for another two seconds, so the value of variable "a" is 300 afterwards. Then instrument 3 is called which performs both, incrementing (in the '+=' short form) and printing, for the first two k-cycles.
EXAMPLE 12B03_pyrun.csd
<CsoundSynthesizer> <CsOptions> -ndm0 </CsOptions> <CsInstruments> kr=100 ;start the python interpreter pyinit ;set variable a to zero at init-time pyruni "a = 0" instr 1 ;increment variable a by one in each k-cycle pyrun "a = a + 1" endin instr 2 ;print out the state of a at this instrument's initialization pyruni "print 'instr 2: a = %d' % a" endin instr 3 ;perform two more increments and print out immediately kCount timeinstk pyrun "a += 1" pyrun "print 'instr 3: a = %d' % a" ;;turnoff after k-cycle number two if kCount == 2 then turnoff endif endin </CsInstruments> <CsScore> i 1 0 1 ;Adds to a for 1 second i 2 1 0 ;Prints a i 1 2 2 ;Adds to a for another two seconds i 3 4 1 ;Prints a again </CsScore> </CsoundSynthesizer> ;Example by Andrés Cabrera and Joachim Heintz
Prints:
instr 2: a = 100
instr 3: a = 301
instr 3: a = 302
Running External Python Scripts: pyexec
Csound allows you to run Python script files that exist outside your csd file. This is done using pyexec. The pyexec opcode will run the script indicated, like this:
pyexec "/home/python/myscript.py"
In this case, the script "myscript.py" will be executed at k-rate. You can give full or relative path names.
There are other versions of the pyexec opcode, which run at initialization only (pyexeci) and others that include an additional trigger argument (pyexect).
Passing values from Python to Csound: pyeval(i)
The opcode pyeval and its relatives, allow you to pass to Csound the value of a Python expression. As usual, the expression is given as a string. So we expect this to work:
Not Working Example!
<CsoundSynthesizer> <CsOptions> -ndm0 </CsOptions> <CsInstruments> pyinit pyruni "a = 1" pyruni "b = 2" instr 1 ival pyevali "a + b" prints "a + b = %d\n", ival endin </CsInstruments> <CsScore> i 1 0 0 </CsScore> </CsoundSynthesizer>
Running this code results in an error with this message:
INIT ERROR in instr 1: pyevali: expression must evaluate in a float
What happens is that Python has delivered an integer to Csound, which expects a floating-point number. Csound always works with numbers which are not integers (to represent a 1, Csound actually uses 1.0). This is equivalent mathematically, but in computer memory these two numbers are stored in a different way. So what you need to do is tell Python to deliver a floating-point number to Csound. This can be done by Python's float() facility. So this code should work:
EXAMPLE 12B04_pyevali.csd
<CsoundSynthesizer> <CsOptions> -ndm0 </CsOptions> <CsInstruments> pyinit pyruni "a = 1" pyruni "b = 2" instr 1 ival pyevali "float(a + b)" prints "a + b = %d\n", ival endin </CsInstruments> <CsScore> i 1 0 0 </CsScore> </CsoundSynthesizer> ;Example by Andrés Cabrera and Joachim Heintz
Prints:
a + b = 3
Passing Values from Csound to Python: pyassign(i)
You can pass values from Csound to Python via the pyassign opcodes. This is a very simple example which calculates the cent distance of the proportion 3/2:
EXAMPLE 12B05_pyassigni.csd
<CsoundSynthesizer>
<CsOptions>
-ndm0
</CsOptions>
<CsInstruments>
pyinit
instr 1 ;assign 3/2 to the python variable "x"
pyassigni "x", 3/2
endin
instr 2 ;calculate cent distance of this proportion
pyruni {{
from math import log
cent = log(x,2)*1200
print cent
}}
endin
</CsInstruments>
<CsScore>
i 1 0 0
i 2 0 0
</CsScore>
</CsoundSynthesizer>
;example by joachim heintz
Unfortunately, you can neither pass strings from Csound to Python via pyassign, nor from Python to Csound via pyeval. So the interchange between both worlds is actually limited to numbers.
Calling Python Functions with Csound Variables
Apart from reading and setting variables directly with an opcode, you can also call Python functions from Csound and have the function return values directly to Csound. This is the purpose of the pycall opcodes. With these opcodes you specify the function to call and the function arguments as arguments to the opcode. You can have the function return values (up to 8 return values are allowed) directly to Csound i- or k-rate variables. You must choose the appropriate opcode depending on the number of return values from the function, and the Csound rate (i- or k-rate) at which you want to run the Python function. Just add a number from 1 to 8 after to pycall, to select the number of outputs for the opcode. If you just want to execute a function without return value simply use pycall. For example, the function "average" defined above, can be called directly from Csound using:
kave pycall1 "average", ka, kb
The output variable kave, will calculate the average of the variable ka and kb at k-rate.
As you may have noticed, the Python opcodes run at k-rate, but also have i-rate versions if an "i" is added to the opcode name. This is also true for pycall. You can use pycall1i, pycall2i, etc. if you want the function to be evaluated at instrument initialization, or in the header. The following csd shows a simple usage of the pycall opcodes:
EXAMPLE 12B06_pycall.csd
<CsoundSynthesizer>
<CsOptions>
-dnm0
</CsOptions>
<CsInstruments>
pyinit
pyruni {{
def average(a,b):
ave = (a + b)/2
return ave
}} ;Define function "average"
instr 1 ;call it
iave pycall1i "average", p4, p5
prints "a = %i\n", iave
endin
</CsInstruments>
<CsScore>
i 1 0 1 100 200
i 1 1 1 1000 2000
</CsScore>
</CsoundSynthesizer>
;example by andrés cabrera and joachim heintz
This csd will print the following output:
a = 150
a = 1500
Local Instrument Scope
Sometimes you want Python variables to be global, and sometimes you may want Python variables to be local to the instrument instance. This is possible using the local Python opcodes. These opcodes are the same as the ones shown above, but have the prefix pyl instead of py. There are opcodes like pylruni, pylcall1t and pylassigni, which will behave just like their global counterparts, but they will affect local Python variables only. It is important to have in mind that this locality applies to instrument instances, not instrument numbers. The next example shows both, local and global behaviour.
EXAMPLE 12B07_local_vs_global.csd
<CsoundSynthesizer> <CsOptions> -dnm0 </CsOptions> <CsInstruments> pyinit giInstanceLocal = 0 giInstanceGlobal = 0 instr 1 ;local python variable 'value' kTime timeinsts pylassigni "value", p4 giInstanceLocal = giInstanceLocal+1 if kTime == 0.5 then kvalue pyleval "value" printks "Python variable 'value' in instr %d, instance %d = %d\n", 0, p1, giInstanceLocal, kvalue turnoff endif endin instr 2 ;global python variable 'value' kTime timeinsts pyassigni "value", p4 giInstanceGlobal = giInstanceGlobal+1 if kTime == 0.5 then kvalue pyleval "value" printks "Python variable 'value' in instr %d, instance %d = %d\n", 0, p1, giInstanceGlobal, kvalue turnoff endif endin </CsInstruments> <CsScore> ; p4 i 1 0 1 100 i 1 0 1 200 i 1 0 1 300 i 1 0 1 400 i 2 2 1 1000 i 2 2 1 2000 i 2 2 1 3000 i 2 2 1 4000 </CsScore> </CsoundSynthesizer> ;Example by Andrés Cabrera and Joachim Heintz
Prints:
Python variable 'value' in instr 1, instance 4 = 100
Python variable 'value' in instr 1, instance 4 = 200
Python variable 'value' in instr 1, instance 4 = 300
Python variable 'value' in instr 1, instance 4 = 400
Python variable 'value' in instr 2, instance 4 = 4000
Python variable 'value' in instr 2, instance 4 = 4000
Python variable 'value' in instr 2, instance 4 = 4000
Python variable 'value' in instr 2, instance 4 = 4000
Both instruments pass the value of the score parameter field p4 to the python variable "value". The only difference is that instrument 1 does this local (with pylassign and pyleval) and instrument 2 does it global (with pyassign and pyeval). Four instances of instrument 1 are called at the same time, for the same duration. Thanks to the local variables, each assignment to the variable "value" stays independent from each other. This is shown when all instances are adviced to print out "value" after 0.5 seconds.
When the four instances of instrument 2 are called, each new instance overwrites the "value" of all previous instances with its own p4. So the second instance sets "value" to 2000 for itself but only for the first instance. The third instance sets "value" to 3000 also for instance one and two. And the fourth instance sets "value" to 4000 for all previous instances, too, and that is shown in the printout, again after 0.5 seconds.
Triggered Versions of Python Opcodes
All of the python opcodes have a "triggered" version, which will only execute when its trigger value is different to 0. The names of these opcodes have a "t" added at the end of them (e.g. pycallt or pylassignt), and all have an additional parameter called ktrig for triggering purposes. See the example in the next chapter for usage.
Simple Markov Chains Using the Python Opcodes
Python opcodes can simplify the creation of complex data structures for algorithmic composition. Below you'll find a simple example of using the Python opcodes to generate Markov chains for a pentatonic scale. Markov chains require in practice building matrices, which start becoming unwieldy in Csound, especially for more than two dimensions. In Python multi-dimensional matrices can be handled as nested lists very easily. Another advange is that the size of matrices (or lists) need not be known in advance, since it is not necessary in python to declare the sizes of lists.
EXAMPLE 12B08_markov.csd
<CsoundSynthesizer>
<CsOptions>
-odac -dm0
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
0dbfs = 1
pyinit
; Python script to define probabilities for each note as lists within a list
; Definition of the get_new_note function which randomly generates a new
; note based on the probabilities of each note occuring.
; Each note list must total 1, or there will be problems!
pyruni {{
c = [0.1, 0.2, 0.05, 0.4, 0.25]
d = [0.4, 0.1, 0.1, 0.2, 0.2]
e = [0.2, 0.35, 0.05, 0.4, 0]
g = [0.7, 0.1, 0.2, 0, 0]
a = [0.1, 0.2, 0.05, 0.4, 0.25]
markov = [c, d, e, g, a]
from random import random, seed
seed()
def get_new_note(previous_note):
number = random()
accum = 0
i = 0
while accum < number:
accum = accum + markov[int(previous_note)] [int(i)]
i = i + 1
return i - 1.0
}}
giSine ftgen 0, 0, 2048, 10, 1 ;sine wave
giPenta ftgen 0, 0, -6, -2, 0, 2, 4, 7, 9 ;Pitch classes for pentatonic scale
instr 1 ;Markov chain reader and note spawner
;p4 = frequency of note generation
;p5 = octave
ioct init p5
klastnote init 0 ;Used to remember last note played (start at first note of scale)
ktrig metro p4 ;generate a trigger with frequency p4
knewnote pycall1t ktrig, "get_new_note", klastnote ;get new note from chain
schedkwhen ktrig, 0, 10, 2, 0, 0.2, knewnote, ioct ;launch note on instrument 2
klastnote = knewnote ;New note is now the old note
endin
instr 2 ;A simple sine wave instrument
;p4 = note to be played
;p5 = octave
ioct init p5
ipclass table p4, giPenta
ipclass = ioct + (ipclass / 100) ; Pitch class of the note
ifreq = cpspch(ipclass) ;Note frequency in Hertz
aenv linen .2, 0.05, p3, 0.1 ;Amplitude envelope
aout poscil aenv, ifreq , giSine ;Simple oscillator
outs aout, aout
endin
</CsInstruments>
<CsScore>
; frequency of Octave of
; note generation melody
i 1 0 30 3 7
i 1 5 25 6 9
i 1 10 20 7.5 10
i 1 15 15 1 8
</CsScore>
</CsoundSynthesizer>
;Example by Andrés Cabrera
- Open a Terminal and type "python". If your python version is not 2.7, download and install the proper version from www.python.org.^
- This printing does not work in CsoundQt. You should run all the examples here in the Terminal.^
C. PYTHON IN CSOUNDQT1
If CsoundQt is built with PythonQt support,2 it enables a lot of new possibilities, mostly in three main fields: interaction with the CsoundQt interface, interaction with widgets and using classes from Qt libraries to build custom interfaces in python.
If you start CsoundQt and can open the panels "Python Console" and "Python Scratch Pad", you are ready to go.
The CsoundQt Python Object
As CsoundQt has formerly been called QuteCsound, this name can still be found in the sources. The QuteCsound object (called PyQcsObject in the sources) is the interface for scripting CsoundQt. All declarations of the class can be found in the file pyqcsobject.h in the sources.
It enables the control of a large part of CsoundQt's possibilities from the python interpreter, the python scratchpad, from scripts or from inside of a running Csound file via Csound's python opcodes.3
By default, a PyQcsObject is already available in the python interpreter of CsoundQt called “q”. To use any of its methods, use form like
q.stopAll()
The methods can be divided into four groups:
- access CsoundQt's interface (open or close files, start or stop performance etc)
- edit Csound files which has already been opened as tabs in CsoundQt
- manage CsoundQt's widgets
- interface with the running Csound engine
File and Control Access
If you have CsoundQt running on your computer, you should type the following code examples in the Python Console (if only one line) or the Python Scratch Pad (if more than one line of code).4
Create or Load a csd File
Type q.newDocument('cs_floss_1.csd') in your Python Console and hit the Return key. This will create a new csd file named "cs_floss_1.csd" in your working directory. And it also returns an integer (in the screenshot below: 3) as index for this file.
If you close this file and then execute the line q.loadDocument('cs_floss_1.csd'), you should see the file again as tab in CsoundQt.
Let us have a look how these two methods newDocument and loadDocument are described in the sources:
int newDocument(QString name) int loadDocument(QString name, bool runNow = false)
The method newDocument needs a name as string ("QString") as argument, and returns an integer. The method loadDocument also takes a name as input string and returns an integer as index for this csd. The additional argument runNow is optional. It expects a boolean value (True/False or 1/0). The default is "false" which means "do not run immediately after loading". So if you type instead q.loadDocument('cs_floss_1.csd', True) or q.loadDocument('cs_floss_1.csd', 1), the csd file should start immediately.
Run, Pause or Stop a csd File
For the next methods, we first need some more code in our csd. So let your "cs_floss_1.csd" look like this:
EXAMPLE 12C01_run_pause_stop.csd
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
0dbfs = 1
nchnls = 1
giSine ftgen 0, 0, 1024, 10, 1
instr 1
kPitch expseg 500, p3, 1000
aSine poscil .2, kPitch, giSine
out aSine
endin
</CsInstruments>
<CsScore>
i 1 0 10
</CsScore>
</CsoundSynthesizer>
This instrument performs a simple pitch glissando from 500 to 1000 Hz in ten seconds. Now make sure that this csd is the currently active tab in CsoundQt, and execute this:
q.play()
This starts the performance. If you do nothing, the performance will stop after ten seconds. If you type instead after some seconds
q.pause()
the performance will pause. The same task q.pause() will resume the performance. Note that this is different from executing q.play() after q.pause() ; this will start a new performance. With
q.stop()
you can stop the current performance.
Access to Different csd Tabs via Indices
The play(), pause() and stop() method, as well as other methods in CsoundQt's integrated Python, allow also to access csd file tabs which are not currently active. As we saw in the creation of a new csd file by q.newDocument('cs_floss_1.csd'), each of them gets an index. This index allows universal access to all csd files in a running CsoundQt instance.
First, create a new file "cs_floss_2.csd", for instance with this code:
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
0dbfs = 1
nchnls = 1
giSine ftgen 0, 0, 1024, 10, 1
instr 1
kPitch expseg 500, p3, 1000
aSine poscil .2, kPitch, giSine
out aSine
endin
</CsInstruments>
<CsScore>
i 1 0 10
</CsScore>
</CsoundSynthesizer>
Now get the index of these two tabs in executing q.getDocument('cs_floss_1.csd') resp. q.getDocument('cs_floss_2.csd') . This will show something like this:
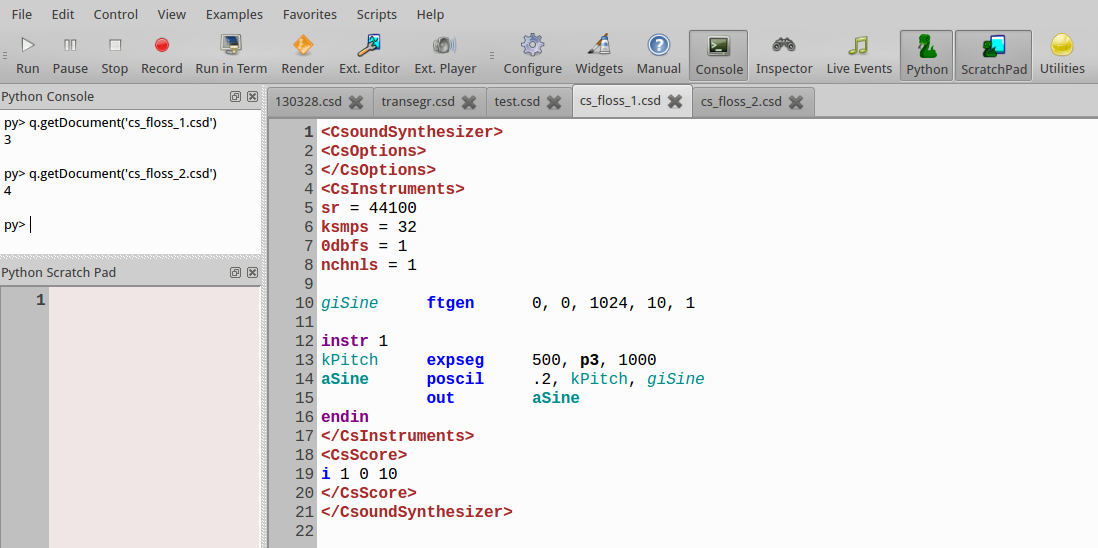
So in my case the indices are 3 and 4.5 Now you can start, pause and stop any of these files with tasks like these:
q.play(3) q.play(4) q.stop(3) q.stop(4)
If you have checked "Allow simultaneous play" in CsoundQt's Configure->General ...

.. you should be able to run both csds simultaneously. To stop all running files, use:
q.stopAll()
To set a csd as active, use setDocument(index). This will have the same effect as clicking on the tab.
Send Score Events
Now comment out the score line in the file "cs_floss_2.csd", or simply remove it. When you now start Csound, this tab should run.6 Now execute this command:
q.sendEvent('i 1 0 2')
This should trigger instrument 1 for two seconds.
Query File Name or Path
In case you need to know the name7 or the path of a csd file, you have these functions:
getFileName() getFilePath()
Calling the method without any arguments, it refers to the currently active csd. An index as argument links to a specific tab. Here is a Python code snippet which returns indices, file names and file paths of all tabs in CsoundQt:
index = 0
while q.getFileName(index):
print 'index = %d' % index
print ' File Name = %s' % q.getFileName(index)
print ' File Path = %s' % q.getFilePath(index)
index += 1
Which returns for instance:
index = 0
File Name = /home/jh/Joachim/Stuecke/30Carin/csound/130328.csd
File Path = /home/jh/Joachim/Stuecke/30Carin/csound
index = 1
File Name = /home/jh/src/csoundmanual/examples/transegr.csd
File Path = /home/jh/src/csoundmanual/examples
index = 2
File Name = /home/jh/Arbeitsfläche/test.csd
File Path = /home/jh/Arbeitsfläche
index = 3
File Name = /home/jh/Joachim/Csound/FLOSS/Release03/Chapter_12C_PythonInCsoundQt/cs_floss_1.csd
File Path = /home/jh/Joachim/Csound/FLOSS/Release03/Chapter_12C_PythonInCsoundQt
index = 4
File Name = /home/jh/Joachim/Csound/FLOSS/Release03/Chapter_12C_PythonInCsoundQt/cs_floss_2.csd
File Path = /home/jh/Joachim/Csound/FLOSS/Release03/Chapter_12C_PythonInCsoundQt
Get and Set csd Text
One of the main features of Python scripting in CsoundQt is the ability to edit any section of a csd file. There are several "get" functions, to query text, and also "set" functions to change or insert text.
Get Text from a csd File
Make sure your "cs_floss_2.csd" is the active tab, and execute the following python code lines:
q.getCsd() q.getOrc() q.getSco()
The q.getOrc() task should return this:
u'\nsr = 44100\nksmps = 32\n0dbfs = 1\nnchnls = 1\n\ngiSine ftgen 0, 0, 1024, 10, 1\n\ninstr 1\nkPitch expseg 1000, p3, 500\naSine poscil .2, kPitch, giSine\n out aSine\nendin\n'
The u'...' indicates that a unicode string is returned. As usual in format expressions, newlines are indicated with the '\n' formatter.
You can also get the text for the <CsOptions>, the text for CsoundQt's widgets and presets, or the full text of this csd:
getOptionsText() getWidgetsText() getPresetsText()getCsd() getFullText()
If you select some text or some widgets, you will get the selection with these commands:
getSelectedText() getSelectedWidgetsText()
As usual, you can specify any of the loaded csds via its index. So calling q.getOrc(3) instead of q.getOrc()will return the orc text of the csd with index 3, instead of the orc text of the currently active csd.
Set Text in a csd File
Set the cursor anywhere in your active csd, and execute the following line in the Python Console:
q.insertText('my nice insertion')
You will see your nice insertion in the csd file. In case you do not like it, you can choose Edit->Undo. It does not make a difference for the CsoundQt editor whether the text has been typed by hand, or by the internal Python script facility.
Text can also be inserted to individual sections using the functions:
setCsd(text) setFullText(text) setOrc(text) setSco(text) setWidgetsText(text) setPresetsText(text) setOptionsText(text)
Note that the whole section will be overwritten with the string text.
Opcode Exists
You can ask whether a string is an opcode name, or not, with the function opcodeExtists, for instance:
py> q.opcodeExists('line')
True
py> q.opcodeExists('OSCsend')
True
py> q.opcodeExists('Line')
False
py> q.opcodeExists('Joe')
NotYet
Example: Score Generation
A typical application for setting text in a csd is to generate a score. There have been numerous tools and programs to do this, and it can be very pleasant to use CsoundQt's Python scripting for this task. Let us modify our previous instrument first to make it more flexible:
EXAMPLE 12C02_score_generated.csd
<CsoundSynthesizer>
<CsOptions>
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 32
0dbfs = 1
nchnls = 1
giSine ftgen 0, 0, 1024, 10, 1
instr 1
iOctStart = p4 ;pitch in octave notation at start
iOctEnd = p5 ;and end
iDbStart = p6 ;dB at start
iDbEnd = p7 ;and end
kPitch expseg cpsoct(iOctStart), p3, cpsoct(iOctEnd)
kEnv linseg iDbStart, p3, iDbEnd
aSine poscil ampdb(kEnv), kPitch, giSine
iFad random p3/20, p3/5
aOut linen aSine, iFad, p3, iFad
out aOut
endin
</CsInstruments>
<CsScore>
i 1 0 10 ;will be overwritten by the python score generator
</CsScore>
</CsoundSynthesizer>
The following code will now insert 30 score events in the score section:
from random import uniform
numScoEvents = 30
sco = ''
for ScoEvent in range(numScoEvents):
start = uniform(0, 40)
dur = 2**uniform(-5, 3)
db1, db2 = [uniform(-36, -12) for x in range(2)]
oct1, oct2 = [uniform(6, 10) for x in range(2)]
scoLine = 'i 1 %f %f %f %f %d %d\n' % (start, dur, oct1, oct2, db1, db2)
sco = sco + scoLine
q.setSco(sco)
This generates a texture with either falling or rising gliding pitches. The durations are set in a way that shorter durations are more frequently than larger ones. The volume and pitch ranges allow many variations in the simple shape.
Widgets
Creating a Label
Click on the "Widgets" button to see the widgets panel. Then execute this command in the Python Console:
q.createNewLabel()
The properties dialog of the label pops up. Type "Hello Label!" or something like this as text.

When you click "Ok", you will see the label widget in the panel, and a strange unicode string as return value in the Python Console:

The string u'{3a171aa2-4cf8-4f05-9f30-172863909f56}' is a "universally unique identifier" (uuid). Each widget can be accessed by this ID.
Specifying the Common Properties as Arguments
Instead of having a live talk with the properties dialog, we can specify all properties as arguments for the createNewLabel method:
q.createNewLabel(200, 100, "second_label")
This should be the result:

A new label has been created—without opening the properties dialog—at position x=200 y=1008 with the name "second_label". If you want to create a widget not in the active document, but in another tab, you can also specify the tab index. This command will create a widget at the same position and with the same name in the first tab:
q.createNewLabel(200, 100, "second_label", 0)
Setting the Specific Properties
Each widget has a xy position and a channel name.9 But the other properties depend on the type of widget. A Display has name, width and height, but no resolution like a SpinBox. The function setWidgetProperty refers to a widget via its ID and sets a property. Let us try this for a Display widget. This command creates a Display widget with channel name "disp_chan_01" at position x=50 y=150:
q.createNewDisplay(50, 150, "disp_chan_01")
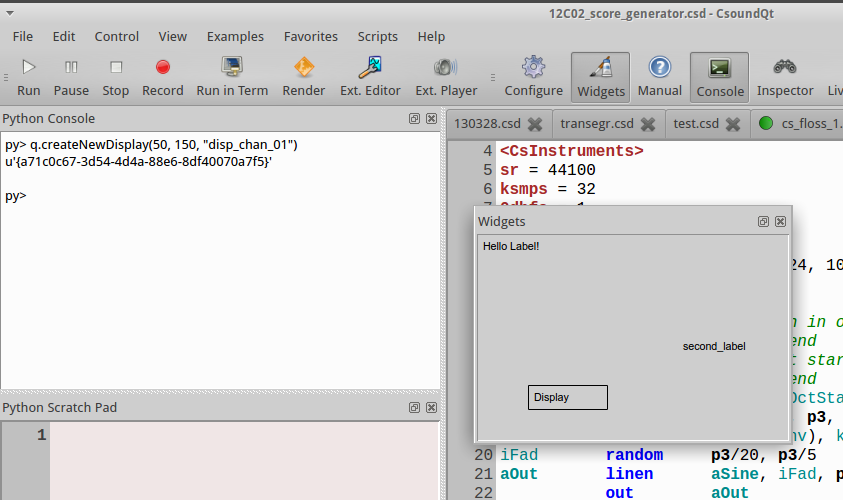
And this sets the text to a new string:10
q.setWidgetProperty("disp_chan_01", "QCS_label", "Hey Joe!")
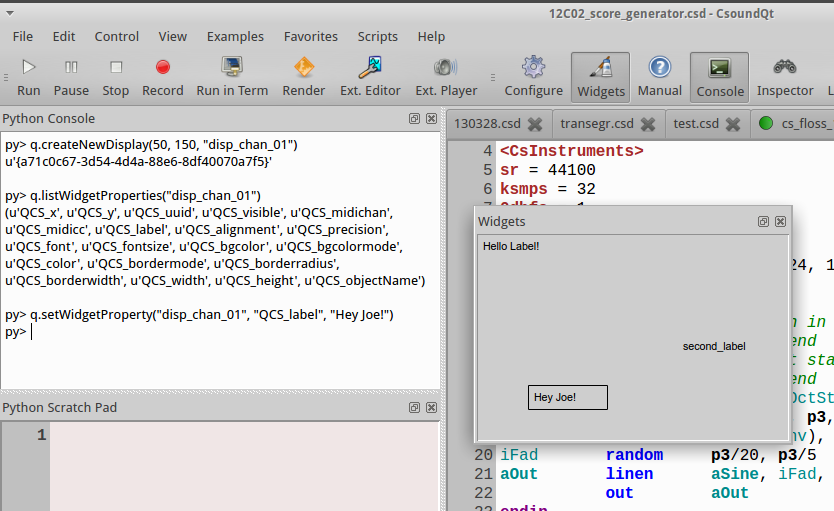
The setWidgetProperty method needs the ID of a widget first. This can be expressed either as channel name ("disp_chan_01") as in the command above, or as uuid. As I got the string u'{a71c0c67-3d54-4d4a-88e6-8df40070a7f5}' as uuid, I can also write:
q.setWidgetProperty(u'{a71c0c67-3d54-4d4a-88e6-8df40070a7f5}', "QCS_label", "Hey Joeboe!")
For humans, referring to the channel name as ID is probably preferable ...11 - But as the createNew... method returns the uuid, you can use it implicitely, for instance in this command:
q.setWidgetProperty(q.createNewLabel(70, 70, "WOW"), "QCS_fontsize", 18)
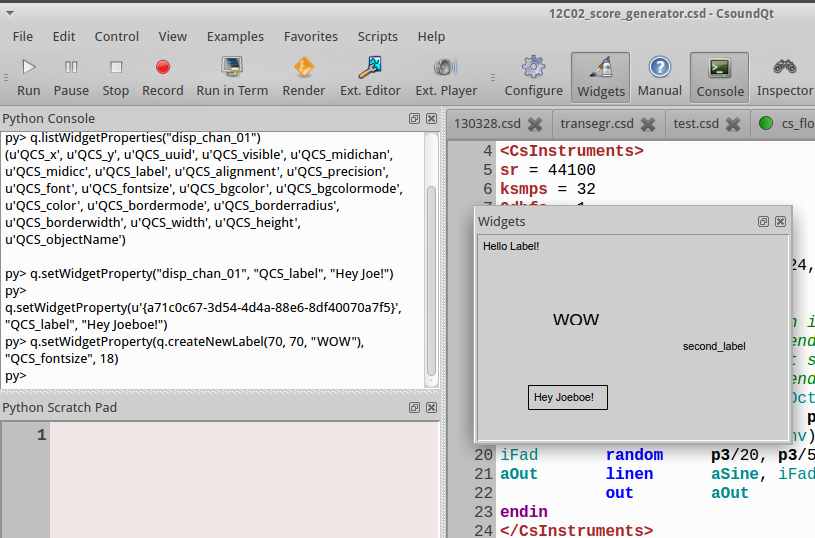
Getting the Property Names and Values
You may have asked how to know that the visible text of a Display widget is called "QCS_label" and the fontsize "QCS_fontsize". If you do not know the name of a property, ask CsoundQt for it via the function listWidgetProperties:
py> q.listWidgetProperties("disp_chan_01")
(u'QCS_x', u'QCS_y', u'QCS_uuid', u'QCS_visible', u'QCS_midichan', u'QCS_midicc', u'QCS_label', u'QCS_alignment', u'QCS_precision', u'QCS_font', u'QCS_fontsize', u'QCS_bgcolor', u'QCS_bgcolormode', u'QCS_color', u'QCS_bordermode', u'QCS_borderradius', u'QCS_borderwidth', u'QCS_width', u'QCS_height', u'QCS_objectName')
As you see, listWidgetProperties returns all properties in a tuple. You can query the value of a single property with the function getWidgetProperty, which takes the uuid and the property as inputs, and returns the property value. So this code snippet asks for all property values of our Display widget:
widgetID = "disp_chan_01"
properties = q.listWidgetProperties(widgetID)
for property in properties:
propVal = q.getWidgetProperty(widgetID, property)
print property + ' = ' + str(propVal)
Returns:
QCS_x = 50
QCS_y = 150
QCS_uuid = {a71c0c67-3d54-4d4a-88e6-8df40070a7f5}
QCS_visible = True
QCS_midichan = 0
QCS_midicc = -3
QCS_label = Hey Joeboe!
QCS_alignment = left
QCS_precision = 3
QCS_font = Arial
QCS_fontsize = 10
QCS_bgcolor = #ffffff
QCS_bgcolormode = False
QCS_color = #000000
QCS_bordermode = border
QCS_borderradius = 1
QCS_borderwidth = 1
QCS_width = 80
QCS_height = 25
QCS_objectName = disp_chan_01
Get the UUIDs of all Widgets
For getting the uuid strings of all widgets in the active csd tab, type
q.getWidgetUuids()

As always, the uuid strings of other csd tabs can be accessed via the index.
Some Examples for Creating and Modifying Widgets
Create a new slider with the channel name "level" at position 10,10 in the (already open but not necessarily active) document "test.csd":
q.createNewSlider(10, 10, "level", q.getDocument("test.csd"))
Create ten knobs with the channel names "partial_1", "partial_2" etc, and the according labels "amp_part_1", "amp_part_2" etc in the currently active document:
for no in range(10):
q.createNewKnob(100*no, 5, "partial_"+str(no+1))
q.createNewLabel(100*no+5, 90, "amp_part_"+str(no+1))Alternatively, you can store the uuid strings while creating:
knobs, labels = [], []
for no in range(10):
knobs.append(q.createNewKnob(100*no, 5, "partial_"+str(no+1)))
labels.append(q.createNewLabel(100*no+5, 90, "amp_part_"+str(no+1)))
The variables knobs and labels now contain the IDs:
py> knobs
[u'{8d10f9e3-70ce-4953-94b5-24cf8d6f6adb}', u'{d1c98b52-a0a1-4f48-9bca-bac55dad0de7}', u'{b7bf4b76-baff-493f-bc1f-43d61c4318ac}', u'{1332208d-e479-4152-85a8-0f4e6e589d9d}', u'{428cc329-df4a-4d04-9cea-9be3e3c2a41c}', u'{1e691299-3e24-46cc-a3b6-85fdd40eac15}', u'{a93c2b27-89a8-41b2-befb-6768cae6f645}', u'{26931ed6-4c28-4819-9b31-4b9e0d9d0a68}', u'{874beb70-b619-4706-a465-12421c6c8a85}', u'{3da687a9-2794-4519-880b-53c2f3b67b1f}']
py> labels
[u'{9715ee01-57d5-407d-b89a-bae2fc6acecf}', u'{71295982-b5e7-4d64-9ac5-b8fbcffbd254}', u'{09e924fa-2a7c-47c6-9e17-e710c94bd2d1}', u'{2e31dbfb-f3c2-43ab-ab6a-f47abb4875a3}', u'{adfe3aef-4499-4c29-b94a-a9543e54e8a3}', u'{b5760819-f750-411d-884c-0bad16d68d09}', u'{c3884e9e-f0d8-4718-8fcb-66e82456f0b5}', u'{c1401878-e7f7-4e71-a097-e92ada42e653}', u'{a7d14879-1601-4789-9877-f636105b552c}', u'{ec5526c4-0fda-4963-8f18-1c7490b0a667}'
Move the first knob 200 pixels downwards:
q.setWidgetProperty( knobs[0], "QCS_y", q.getWidgetProperty(knobs[0], "QCS_y")+200)
Modify the maximum of each knob so that the higher partials have less amplitude range (set maximum to 1, 0.9, 0.8, ..., 0.1):
for knob in range(10):
q.setWidgetProperty(knobs[knob], "QCS_maximum", 1-knob/10.0)
Deleting widgets
You can delete a widget using the method destroyWidget. You have to pass the widget's ID, again either as channel name or (better) as uuid string. This will remove the first knob in the example above:
q.destroyWidget("partial_1")
This will delete all knobs:
for w in knobs:
q.destroyWidget(w)
And this will delete all widgets of the active document:
for w in q.getWidgetUuids():
q.destroyWidget(w)
Getting and Setting Channel Names and Values
After this cruel act of destruction, let us again create a slider and a display:
py> q.createNewSlider(10, 10, "level")
u'{b0294b09-5c87-4607-afda-2e55a8c7526e}'
py> q.createNewDisplay(50, 10, "message")
u'{a51b438f-f671-4108-8cdb-982387074e4d}'
Now we will ask for the values of these widgets12 with the methods getChannelValue and getChannelString:
py> q.getChannelValue('level')
0.0
py> q.getChannelString("level")
u''
py> q.getChannelValue('message')
0.0
py> q.getChannelString('message')
u'Display'
As you see, it depends on the type of the widget whether to query its value by getChannelValue or getChannelString. Although CsoundQt will not return an error, it makes no sense to ask a slider for its string (as its value is a number), and a display for its number (as its value is a string).
With the methods setChannelValue and setChannelString we can change the main content of a widget very easily:
py> q.setChannelValue("level", 0.5)
py> q.setChannelString("message", "Hey Joe again!")
This is much more handy than the general method using setWidgetProperty:
py> q.setWidgetProperty("level", "QCS_value", 1)
py> q.setWidgetProperty("message", "QCS_label", "Nono")
Presets
Now right-click in the widget panel and choose Store Preset -> New Preset:
You can (but need not) enter a name for the preset. The important thing here is the number of the preset (here 0). - Now change the value of the slider and the text of the display widget. Save again as preset, now being preset 1. - Now execute this:
q.loadPreset(0)
You will see the content of the widgets reloaded to the first preset. Again, with
q.loadPreset(1)
you can switch to the second one.
Like all python scripting functions in CsoundQt, you can not only use these methods from the Python Console or the Python Cratch Pad, but also from inside any csd. This is an example how to switch all the widgets to other predefined states, in this case controlled by the score. You will see the widgets for the first three seconds in Preset 0, then for the next three seconds in Preset 1, and finally again in Preset 0:
EXAMPLE 12C03_presets.csd
<CsoundSynthesizer> <CsOptions> -odac </CsOptions> <CsInstruments> pyinit instr loadPreset index = p4 pycalli "q.loadPreset", index endin </CsInstruments> <CsScore> i "loadPreset" 0 3 0 i "loadPreset" + . 1 i "loadPreset" + . 0 </CsScore> </CsoundSynthesizer> ;example by tarmo johannes and joachim heintz
Csound Functions
Several functions can interact with the Csound engine, for example to query information about it. Note that the functions getSampleRate, getKsmps, getNumChannels and getCurrentCsound refer to a running instance of Csound.
py> q.getVersion() # CsoundQt API version u'1.0' py> q.getSampleRate() 44100.0 py> q.getKsmps() 32 py> q.getNumChannels() 1 py> q.getCurrentCsound() CSOUND (C++ object at: 0x2fb5670)
With getCsChannel, getCsStringChannel and setCsChannel you can access csound channels directly, independently from widgets. They are useful when testing a csd for use with the Csound API (in another application, a csLapdsa or Cabbage plugin, Android application) or similar. These are some examples, executed on a running csd instance:
py> q.getCsChannel('my_num_chn')
0.0
py> q.getCsStringChannel('my_str_chn')
u''
py> q.setCsChannel('my_num_chn', 1.1)
py> q.setCsChannel('my_str_chn', 'Hey Csound')
py> q.getCsChannel('my_num_chn')
1.1
py> q.getCsStringChannel('my_str_chn')
u'Hey Csound'
If you have a function table in your running Csound instance which has for instance been created with the line giSine ftgen 1, 0, 1024, 10, 1, you can query getTableArray like this:
py> q.getTableArray(1) MYFLT (C++ object at: 0x35d1c58)
Finally, you can register a Python function as a callback to be executed in between processing blocks for Csound. The first argument should be the text that should be called on every pass. It can include arguments or variables which will be evaluated every time. You can also set a number of periods to skip to avoid.
registerProcessCallback(QString func, int skipPeriods = 0)
You can register the python text to be executed on every Csound control block callback, so you can execute a block of code, or call any function which is already defined.
Creating Own GUIs with PythonQt
One of the very powerful features of using Python inside CsoundQt is the ability to build own GUIs. This is done via the PythonQt library which gives you access to the Qt toolkit via Python. We will show some examples here. Have a look in the "Scripts" menu in CsoundQt to find much more (you will find the code in the "Editor" submenu).
Dialog Box
Sometimes it is practical to ask from user just one question - number or name of something and then execute the rest of the code (it can be done also inside a csd with python opcodes). In Qt, the class to create a dialog for one question is called QInputDialog.
To use this or any other Qt classes, it is necessary to import the PythonQt and its Qt submodules. In most cases it is enough to add this line:
from PythonQt.Qt import *
or
from PythonQt.QtGui import *
At first an object of QInputDialog must be defined, then you can use its methods getInt, getDouble, getItem or getText to read the input in the form you need. This is a basic example:
from PythonQt.Qt import * inpdia = QInputDialog() myInt = inpdia.getInt(inpdia,"Example 1","How many?") print myInt # example by tarmo johannes
Note that the variable myInt is now set to a value which remains in your Python interpreter. Your Python Console may look like this when executing the code above, and then ask for the value of myInt:
py> 12 Evaluated 5 lines. py> myInt 12
Depending on the value of myInt, you can do funny or serious things. This code re-creates the Dialog Box whenever the user enters the number 1:
from PythonQt.Qt import *
def again():
inpdia = QInputDialog()
myInt = inpdia.getInt(inpdia,"Example 1","How many?")
if myInt == 1:
print "If you continue to enter '1' I will come back again and again."
again()
else:
print "Thanks - Leaving now."
again()
# example by joachim heintz
This is a simple example showing how you can embed an own GUI in your Csound code. Here, Csound waits for the user input, and the prints out the entered value as the Csound variable giNumber:
EXAMPLE 12C04_dialog.csd
<CsoundSynthesizer>
<CsOptions>
-n
</CsOptions>
<CsInstruments>
pyinit
pyruni {{
from PythonQt.Qt import *
dia = QInputDialog()
dia.setDoubleDecimals(4)
}}
giNumber pyevali {{
dia.getDouble(dia,"CS question","Enter number: ")
}} ; get the number from Qt dialog
instr 1
print giNumber
endin
</CsInstruments>
<CsScore>
i 1 0 0
</CsScore>
</CsoundSynthesizer>
;example by tarmo johannes
Simple GUI with Buttons
The next example takes the user input (as a string) and transforms it to a sounding sequence of notes. First, make sure that the following csd is your active tab in CsoundQt:EXAMPLE 12C05_string_sound.csd
<CsoundSynthesizer>
<CsInstruments>
sr = 44100
nchnls = 2
0dbfs = 1
ksmps = 32
giSine ftgen 1, 0, 4096, 10, 1 ; sine
#define MAINJOB(INSTNO) #
Sstr strget p4
ilen strlen Sstr
ipos = 0
marker: ; convert every character in the string to pitch
ichr strchar Sstr, ipos
icps = cpsmidinn(ichr)-$INSTNO*8
;print icps
event_i "i", "sound", 0+ipos/8, p3, ichr,icps, $INSTNO ; chord with arpeggio
loop_lt ipos, 1, ilen, marker
#
instr 1
$MAINJOB(1)
endin
instr 2
$MAINJOB(2)
endin
instr 3
$MAINJOB(3)
endin
instr sound
ichar = p4
ifreq = p5
itype = p6
kenv linen 0.1,0.1, p3,0.5
if itype== 1 then
asig pluck kenv,ifreq,ifreq,0, 3, 0
elseif itype==2 then
kenv adsr 0.05,0.1,0.5,1
asig poscil kenv*0.1,ifreq,giSine
else
asig buzz kenv,ifreq,10, giSine
endif
outs asig,asig
endin
</CsInstruments>
<CsScore>
f0 3600
i 1 0 4 "huhuu"
</CsScore>
</CsoundSynthesizer>
;example by tarmo johannes
Now copy this Python code into your Python Scratch Pad and evaluate it. Then type anything in the "type here" box and push the "insert" button. After pushing "play", the string will be played. You can also send the string as real-time event, to different instruments, in different durations.
from PythonQt.Qt import *
# FUNCTIONS==============================
def insert(): # read input from UI and insert a line to score of csd file, open in CsoundQt with index csdIndex
scoreLine = "f0 3600\n" + "i " + instrSpinBox.text + " 0 " + durSpinBox.text + ' "' + par1LineEdit.text + "\""
print scoreLine
q.setSco(scoreLine, csdIndex)
def play(): # play file with index csdIndex
print "PLAY"
q.play(csdIndex)
def send(): # read input from UI send live event
scoreLine = "i " + instrSpinBox.text + " 0 " + durSpinBox.text + ' "' + par1LineEdit.text + "\""
print scoreLine
q.sendEvent(csdIndex, scoreLine)
def stopAndClose(): #stop csdIndex, close UI
print "STOP"
q.stop(csdIndex)
window.delete()
# MAIN ====================================
window = QWidget() # window as main widget
layout = QGridLayout(window) # use gridLayout - the most flexible one - to place the widgets in a table-like structure
window.setLayout(layout)
window.setWindowTitle("PythonQt inteface example")
instrLabel = QLabel("Select instrument")
layout.addWidget(instrLabel,0,0) # first row, first column
instrSpinBox = QSpinBox(window)
instrSpinBox.setMinimum(1)
instrSpinBox.setMaximum(3)
layout.addWidget(instrSpinBox, 0, 1) # first row, second column
durLabel = QLabel("Duration: ")
layout.addWidget(durLabel,1,0) # etc
durSpinBox = QSpinBox(window)
durSpinBox.setMinimum(1)
durSpinBox.setMaximum(20)
durSpinBox.setValue(3)
layout.addWidget(durSpinBox, 1, 1)
par1Label = QLabel("Enter string for parameter 1: ")
layout.addWidget(par1Label,2,0)
par1LineEdit = QLineEdit(window)
par1LineEdit.setMaxLength(30) # don't allow too long strings
par1LineEdit.setText("type here")
layout.addWidget(par1LineEdit,2,1)
insertButton = QPushButton("Insert",window)
layout.addWidget(insertButton, 3,0)
playButton = QPushButton("Play",window)
layout.addWidget(playButton, 3,1)
sendButton = QPushButton("Send event",window)
layout.addWidget(sendButton, 4,0)
closeButton = QPushButton("Close",window)
layout.addWidget(closeButton, 4,1)
# connect buttons and functions ================
#NB! function names must be without parenthesis!
# number and type of arguments of the signal and slot (called function) must match
insertButton.connect(SIGNAL("clicked()"),insert ) # when clicked, run function insert()
playButton.connect(SIGNAL("clicked()"),play) #etc
sendButton.connect(SIGNAL("clicked()"),send)
closeButton.connect(SIGNAL("clicked()"),stopAndClose)
window.show() # show the window and wait for clicks on buttons
A Color Controller
To illustrate how to use power of Qt together with CsoundQt, the following example uses the color picking dialog of Qt. When user moves the cursor around in the RGB palette frame, the current red-green-blue values are forwarded to CsoundQt as floats in 0..1, visualized as colored meters and used as controlling parameters for sound.
Qt's object QColorDialog emits the signal currentColorChanged(QColor) every time when any of the RGB values in the colorbox has changed. The script connects the signal to a function that forwards the color values to Csound. So with one mouse movement, three parameters can be controlled instantly.
In the Csound implementation of this example I used - thinking on the colors - three instruments from Richard Boulanger's "Trapped in convert" - red, green and blue. The RGB values of the dialog box control the mix between these three instruments.
As usual, let the following csd be your active tab in CsoundQt, then run the Python code in the Python Scratch Pad.13
EXAMPLE 12C06_color_controller.csd
<CsoundSynthesizer>
<CsInstruments>
sr = 44100
ksmps = 32
nchnls = 2
garvb init 0
alwayson "_reverb"
;============================================================================;
;==================================== RED ===================================;
;============================================================================;
; parameters from original score
;i 8 15.5 3.1 3 50 4000 129 8 2.6 0.3
instr red
ifuncl = 16
p4 = 2.2 ; amp
p5 = 50 ; FilterSweep StartFreq
p6 = 4000 ; FilterSweep EndFreq
p7= 129 ; bandwidth
p8 = 8 ; cps of rand1
p9 = 2.6 ; cps of rand2
p10 = 0.3 ; reverb send factor
k1 expon p5, p3, p6
k2 line p8, p3, p8 * .93
k3 phasor k2
k4 table k3 * ifuncl, 20
anoise rand 8000
aflt1 reson anoise, k1, 20 + (k4 * k1 / p7), 1
k5 linseg p6 * .9, p3 * .8, p5 * 1.4, p3 * .2, p5 * 1.4
k6 expon p9 * .97, p3, p9
k7 phasor k6
k8 tablei k7 * ifuncl, 21
aflt2 reson anoise, k5, 30 + (k8 * k5 / p7 * .9), 1
abal oscil 1000, 1000, 1
a3 balance aflt1, abal
a5 balance aflt2, abal
k11 linen p4, .15, p3, .5
a3 = a3 * k11
a5 = a5 * k11
k9 randh 1, k2
aleft = ((a3 * k9) * .7) + ((a5 * k9) * .3)
k10 randh 1, k6
aright = ((a3 * k10) * .3)+((a5 * k10) * .7)
klevel invalue "red"
klevel port klevel,0.05
outs aleft*klevel, aright*klevel
garvb = garvb + (a3 * p10)*klevel
endin
;============================================================================;
;==================================== BLUE ==================================;
;============================================================================;
;i 2 80.7 8 0 8.077 830 0.7 24 19 0.13
instr blue ; p6 = amp
p5 = 8.077 ; pitch
p6 = 830 ; amp
p7 = 0.7 ; reverb send factor
p8 = 24 ; lfo freq
p9 = 19 ; number of harmonic
p10 = 0.1+rnd(0.2) ;0.5 ; sweep rate
ifreq random 500,1000;cpspch(p5)
k1 randi 1, 30
k2 linseg 0, p3 * .5, 1, p3 * .5, 0
k3 linseg .005, p3 * .71, .015, p3 * .29, .01
k4 oscil k2, p8, 1,.2
k5 = k4 + 2
ksweep linseg p9, p3 * p10, 1, p3 * (p3 - (p3 * p10)), 1
kenv expseg .001, p3 * .01, p6, p3 * .99, .001
asig gbuzz kenv, ifreq + k3, k5, ksweep, k1, 15
klevel invalue "blue"
klevel port klevel,0.05
asig = asig*klevel
outs asig, asig
garvb = garvb + (asig * p7)
endin
;============================================================================;
;==================================== GREEN =================================;
;============================================================================;
; i 5 43 1.1 9.6 3.106 2500 0.4 1.0 8 3 17 34
instr green ; p6 = amp
p5 = 3.106 ; pitch
p6 = 2500 ; amp
p7 = 0.4 ; reverb send
p8 = 0.5 ; pan direction
p9 = 8 ; carrier freq
p10 = 3 ; modulator freq
p11 = 17 ; modulation index
p12 = 34 ; rand freq
ifreq = cpspch(p5) ; p7 = reverb send factor
; p8 = pan direction
k1 line p9, p3, 1 ; ... (1.0 = L -> R, 0.1 = R -> L)
k2 line 1, p3, p10 ; p9 = carrier freq
k4 expon 2, p3, p12 ; p10 = modulator freq
k5 linseg 0, p3 * .8, 8, p3 * .2, 8 ; p11 = modulation index
k7 randh p11, k4 ; p12 = rand freq
k6 oscil k4, k5, 1, .3
kenv1 linen p6, .03, p3, .2
a1 foscil kenv1, ifreq + k6, k1, k2, k7, 1
kenv2 linen p6, .1, p3, .1
a2 oscil kenv2, ifreq * 1.001, 1
amix = a1 + a2
kpan linseg int(p8), p3 * .7, frac(p8), p3 * .3, int(p8)
klevel invalue "green"
klevel port klevel,0.05
amix = amix*klevel
outs amix * kpan, amix * (1 - kpan)
garvb = garvb + (amix * p7)
endin
instr _reverb
p4 = 1/10 ; p4 = panrate
k1 oscil .5, p4, 1
k2 = .5 + k1
k3 = 1 - k2
asig reverb garvb, 2.1
outs asig * k2, (asig * k3) * (-1)
garvb = 0
endin
</CsInstruments>
<CsScore>
;============================================================================;
;========================= FUNCTIONS ========================================;
;============================================================================;
f1 0 8192 10 1
; 15 - vaja
f15 0 8192 9 1 1 90
;kasutusel red
f16 0 2048 9 1 3 0 3 1 0 6 1 0
f20 0 16 -2 0 30 40 45 50 40 30 20 10 5 4 3 2 1 0 0 0
f21 0 16 -2 0 20 15 10 9 8 7 6 5 4 3 2 1 0 0
r 3 COUNT
i "red" 0 20
i "green" 0 20
i "blue" 0 6
i . + 3
i . + 4
i . + 7
s
f 0 1800
</CsScore>
</CsoundSynthesizer>
;example by tarmo johannes, after richard boulanger
from PythonQt.Qt import *
# write the current RGB values as floats 0..1 to according channels of "rgb-widgets.csd"
def getColors(currentColor):
q.setChannelValue("red",currentColor.redF(),csd)
q.setChannelValue("green",currentColor.greenF(),csd)
q.setChannelValue("blue",currentColor.blueF(),csd)
# main-----------
cdia = QColorDialog() #create QColorDiaog object
cdia.connect(SIGNAL("currentColorChanged(QColor)"),getColors) # create connection between color changes in the dialog window and function getColors
cdia.show() # show the dialog window,
q.play(csd) # and play the csd
List of PyQcsObject Methods in CsoundQt
Load/Create/Activate a csd File
int loadDocument(QString name, bool runNow = false) int getDocument(QString name = "") int newDocument(QString name) void setDocument(int index)
Play/Pause/Stop a csd File
void play(int index = -1, bool realtime = true) void pause(int index = -1) void stop(int index = -1) void stopAll()
Send Score Events
void sendEvent(int index, QString events) void sendEvent(QString events) void schedule(QVariant time, QVariant event)
Query File Name/Path
QString getFileName(int index = -1) QString getFilePath(int index = -1)
Get csd Text
QString getSelectedText(int index = -1, int section = -1) QString getCsd(int index = -1) QString getFullText(int index = -1) QString getOrc(int index = -1) QString getSco(int index = -1) QString getWidgetsText(int index = -1) QString getSelectedWidgetsText(int index = -1) QString getPresetsText(int index = -1) QString getOptionsText(int index = -1)
Set csd Text
void insertText(QString text, int index = -1, int section = -1) void setCsd(QString text, int index = -1) void setFullText(QString text, int index = -1) void setOrc(QString text, int index = -1) void setSco(QString text, int index = -1) void setWidgetsText(QString text, int index = -1) void setPresetsText(QString text, int index = -1) void setOptionsText(QString text, int index = -1)
Opcode Exists
bool opcodeExists(QString opcodeName)
Create Widgets
QString createNewLabel(int x = 0, int y = 0, QString channel = QString(), int index = -1) QString createNewDisplay(int x = 0, int y = 0, QString channel = QString(), int index = -1) QString createNewScrollNumber(int x = 0, int y = 0, QString channel = QString(), int index = -1) QString createNewLineEdit(int x = 0, int y = 0, QString channel = QString(), int index = -1) QString createNewSpinBox(int x = 0, int y = 0, QString channel = QString(), int index = -1) QString createNewSlider(QString channel, int index = -1) QString createNewSlider(int x = 0, int y = 0, QString channel = QString(), int index = -1) QString createNewButton(int x = 0, int y = 0, QString channel = QString(), int index = -1) QString createNewKnob(int x = 0, int y = 0, QString channel = QString(), int index = -1) QString createNewCheckBox(int x = 0, int y = 0, QString channel = QString(), int index = -1) QString createNewMenu(int x = 0, int y = 0, QString channel = QString(), int index = -1) QString createNewMeter(int x = 0, int y = 0, QString channel = QString(), int index = -1) QString createNewConsole(int x = 0, int y = 0, QString channel = QString(), int index = -1) QString createNewGraph(int x = 0, int y = 0, QString channel = QString(), int index = -1) QString createNewScope(int x = 0, int y = 0, QString channel = QString(), int index = -1)
Query Widgets
QVariant getWidgetProperty(QString widgetid, QString property, int index= -1) double getChannelValue(QString channel, int index = -1) QString getChannelString(QString channel, int index = -1) QStringList listWidgetProperties(QString widgetid, int index = -1) QStringList getWidgetUuids(int index = -1)
Modify Widgets
void setWidgetProperty(QString widgetid, QString property, QVariant value, int index= -1) void setChannelValue(QString channel, double value, int index = -1) void setChannelString(QString channel, QString value, int index = -1)
Delete Widgets
bool destroyWidget(QString widgetid)
Presets
void loadPreset(int presetIndex, int index = -1)
Live Event Sheet
QuteSheet* getSheet(int index = -1, int sheetIndex = -1) QuteSheet* getSheet(int index, QString sheetName)
Csound / API
QString getVersion() void refresh() void setCsChannel(QString channel, double value, int index = -1) void setCsChannel(QString channel, QString value, int index = -1) double getCsChannel(QString channel, int index = -1) QString getCsStringChannel(QString channel, int index = -1) CSOUND* getCurrentCsound() double getSampleRate(int index = -1) int getKsmps(int index = -1) int getNumChannels(int index = -1) MYFLT *getTableArray(int ftable, int index = -1) void registerProcessCallback(QString func, int skipPeriods = 0, int index = -1)
- This chapter is based on Andrés Cabrera's paper Python Scripting in QuteCsound at the Csound Conference in Hannover (2011).^
- This should be the case for CsoundQt 0.7 or higher on OSX. On Windows, the corrent version 0.7.0 is built with PythonQt support. You must have installed Python 2.7, too. For building CsoundQt with Python support, have a look at the descriptions in http://sourceforge.net/apps/mediawiki/qutecsound.^
- See chapter 12B for more information on these.^
- To evaluate multiple lines of Python code in the Scratch Pad, choose either Edit->Evaluate Section (Alt+E), or select and choose Edit->Evaluate Selection (Alt+Shift+E).^
- If you have less or more csd tabs already while creating the new files, the index will be lower or higher.^
- If not, you are probably using an older version of Csound. In this case, insert the scoreline "f 0 99999", and this csd will run and wait for your real-time score events for 99999 seconds.^
- Different to most usages, 'name' means here the full path including the file name.^
- Pixels from left resp. from top.^
- Only a label does not have a channel name. So as we saw, in case of a label the name is its displayed text.^
- For the main property of a widget (text for a Display, number for Sliders, SpinBoxes etc) you can also use the setChannelString and setChannelValue method. See below at "Getting and Setting Channel Values" ^
- Note that two widgets can share the same channel name (for instance a slider and a spinbox). In this case, referring to a widget via its channel name is not possible at all.^
- Here again accessed by the channel name. Of course accessing by uuid would also be possible (and more safe, as explained above).^
- The example should also be availiable in CsoundQt's Scripts menu.^
D. LUA IN CSOUND
Have a look at Michael Gogins' paper Writing Csound Opcodes in Lua at the Csound Conference in Hannover (there is also a video from the workshop at www.youtube.com/user/csconf2011).
CSOUND IN iOS
Note: this chapter can be found in PDF form here and the Csound iOS SDK can be downloaded here.
1 Introduction
This guide aims to introduce and illustrate some of the power that the Csound language offers to iOS Developers. It assumes that the reader has a rudimentary background in Csound, and some experience and understanding of iOS development with either Swift or Objective-C.
1.1 Csound for iOS
Csound for iOS offers the developer a number of powerful tools have been created to aid in the development of audio software for Apple's iOS platform. Here we describe a promising avenue for audio programmers, and especially for those with some background in Csound: the Csound for iOS API. We hope that it will serve as a guide to those who hope to advance or diversify as audio programmers for iOS by harnessing the powerful synthesis, signal-processing, and other capabilities of Csound and the Csound API.
The Csound for iOS Manual (Lazzarini, Yi, Boulanger) that ships with the Csound for iOS API is intended to serve as a lighter reference for developers. This guide is distinct from it in that it is intended to be a more thorough, step-by-step approach to learning the API for the first time.
2 Getting Started
There are a number of ways in which one might begin to learn to work with the Csound for iOS API. Here, to aid in exploring it, we first describe how the project of examples that ships with the API is structured. We then talk about how to go about configuring a new iOS Xcode project to work with Csound from scratch.
2.1 Csound for iOS Examples
The Csound for iOS Examples project contains a number of simple examples (in both Objective-C and Swift) of how one might use Csound’s synthesis and signal processing capabilities, and the communicative functionality of the API.
In the ’ViewControllers’ group, a number of subgroups exist to organize the various individual examples into a single application. This is done using the Master-Detail application layout paradigm, wherein a set of options, all of them listed in a ’master’ table, correlates to a single ’detail’ ViewController. Familiar examples of this design model, employed by Apple and provided with every iOS device, are the Settings app, and the Notes app – each of these contains a master table upon which the detail ViewController’s content is predicated.
In each of these folders, you will find a unique example showcasing how one might use some of the features of the Csound for iOS API to communicate with Csound to produce and process sounds and make and play music. These are designed to introduce you to these features in a practical setting, and etch of these has a unifying theme that informs its content, interactions, and structure.
2.2 Adding Csound to Your Project
If you are working in Objective-C, adding Csound for iOS to your project is as simple as dragging the csound-iOS folder into your project. You should select "Groups" rather than "Folder References", and it is recommended that you elect to copy the csound-iOS folder into your project folder ("Copy Items if Needed").
Once you have successfully added this folder, including the CsoundObj class (the class that manages Csound on iOS) is as simple as adding an import statement to the class. For example:
//
// ViewController.h
//
#import "CsoundObj.h"
Note that this only makes the CsoundObj class available, which provides an interface for Csound. There are other objects containing UI and CoreMotion bindings, as well as MIDI handling. These are discussed later in this document, and other files will need to be imported in order to access them.
For Swift users, the process is slightly different: you will need to first create a "bridging header": a .h header file that can import the Objective-C API for access in Swift. The naming convention is [YourProjectName]-Bridging Header.h and this file can be easily created manually in Xcode by choosing File > New > File > Header File (Under ’Source’), and using the naming convention described above. After this, you will need to navigate to your project build settings and add the path to this file (relative to your project’s .xcodeproj project file).
Once this is done, navigate to the bridging header in Xcode and add your Objective-C #import statements here. For example:
//
// CsoundiOS_ExampleSwift-Bridging-Header.h
// CsoundiOS_ExampleSwift
//
#ifndef CsoundiOS_ExampleSwift_Bridging_Header_h
#define CsoundiOS_ExampleSwift_Bridging_Header_h
#import "CsoundObj.h"
#endif /* CsoundiOS_ExampleSwift_Bridging_Header_h */
You do not need to add any individual import statements to Swift files, CsoundObj’s functionality should be accessible in your .swift files after this process is complete.
2.3 Playing a .csd File
The first thing we will do so that we can play a .csd file is add our .csd file to our project. In this case, we will add a simple .csd (in this case named test.csd) that plays a sine tone with a frequency of 440Hz for ten seconds. Sample Csound code for this is:
<CsoundSynthesizer>
<CsOptions>
-odac
</CsOptions>
<CsInstruments>
sr = 44100
ksmps = 128
nchnls = 2
0dbfs = 1
instr 1
asig poscil 0.5 , 440
outs asig , asig
endin
</CsInstruments>
<CsScore>
i1 0 10
</CsScore>
</CsoundSynthesizer>
We will add this to our Xcode project by dragging and dropping it into our project’s main folder, making sure to select "Copy items if needed" and to add it to our main target.
In order to play this .csd file, we must first create an instance of the CsoundObj class. We can do this by creating a property of our class as follows, in our .h file (for example, in ViewController.h):
//
// ViewController.h
// CsoundiOS_ExampleProject
//
#import <UIKit/UIKit.h>
#import "CsoundObj.h"
@interface ViewController : UIViewController
@property CsoundObj *csound;
@end
Once we’ve done this, we can move over to the corresponding .m file (in this case, ViewController.m) and instantiate our Csound object. Here we will do this in our viewDidLoad method, that is called when our ViewController’s view loads.
//
// ViewController.m
// CsoundiOS_ExampleProject
//
@interface ViewController()
@end
@implementation ViewController
- (void)viewDidLoad {
[super viewDidLoad];
// Allocate memory for and initialize a CsoundObj
self.csound = [[CsoundObj alloc] init];
}
Note: in order to play our .csd file, we must first get a path to it that we can give Csound. Because part of this path can vary depending on certain factors (for example, the user’s native language setting), we cannot pass a static or "hard-coded" path. Instead, we will access the file using the NSBundle class (or ’Bundle’ in Swift).
The .csd file is copied as a resource (you can see this under the ’Build Phases’ tab in your target’s settings), and so we will access it and tell Csound to play it as follows:
- (void)viewDidLoad {
[super viewDidLoad];
self.csound = [[CsoundObj alloc] init];
//CsoundObj *csound is declared as a property in .h
NSString *pathToCsd = [[NSBundle mainBundle pathForResource: @"test" ofType:@ "csd"];
[self.csound play:pathToCsd];
}
Note that in Swift, this is a little easier and we can simply use:
import UIKit
class ViewController: UIViewController {
var csound = CsoundObj()
override func viewDidLoad() {
super.viewDidLoad()
let pathToCsd = Bundle.main.path(forResource: "test", ofType: "csd")
self.csound.play(pathToCsd)
}
}
With this, the test.csd file should load and play, and we should hear a ten-second long sine tone shortly after the application runs (i.e. when the main ViewController’s main view loads).
3 Recording and Rendering
3.1 Recording (Real-Time)
To record the output of Csound in real-time, instead of the play method, use:
// Objective-C
NSURL *docsDirURL = [[[NSFileManager defaultManager] URLsForDirectory:NSDocumentDirectory inDomains:NSUserDomainMask] lastObject];
NSURL *file = [docsDirURL URLByAppendingPathComponent:@"outputFile.aif"]];
NSString *csdPath = [[NSBundle mainBundle] pathForResource:@"csdToRecord" ofType:@"csd"];
[self.csound record:csdPath toURL:file];
// Swift
let docsDirURL = FileManager.default.urls(for: .documentDirectory, in: .userDomainMask)[0]
let file = docsDirURL.appendingPathComponent("outFile.aif")
let csdPath = Bundle.main.path(forResource: "csdFile", ofType: "csd")
csound.record(csdPath, to: file)
Alternatively, the recordToURL method can be used while Csound is already running to begin recording:
// Objective-C
NSURL *docsDirURL = [[[NSFileManager defaultManager] URLsForDirectory:NSDocumentDirectory inDomains:NSUserDomainMask] lastObject];
NSURL *file = [docsDirURL URLByAppendingPathComponent:@"outputFile.aif"]];
[self.csound recordToURL:file];
// Swift
let docsDirURL = FileManager.default.urls(for: .documentDirectory, in: .userDomainMask)[0]
let file = docsDirURL.appendingPathComponent("outFile.aif")
csound.record(to: file)
Note: the stopRecording method is used to stop recording without also stopping Csound’s real-time rendering.
3.2 Rendering (Offline)
You can also render a .csd to an audio file offline. To render Csound offline to disk, use the record:toFile: method, which takes a path rather than a URL as its second argument. For example:
// Objective-C
NSString *docsDir = NSSearchPathForDirectoriesInDomains(NSDocumentDirectory, NSUserDomainMask, YES)[0];
NSString *file = [docsDir stringByAppendingPathComponent:@"outFile.aif"];
NSString *csdPath = [[NSBundle mainBundle] pathForResource:@"csdFile" ofType:@"csd"];
[self record:csdPath toFile:file];
// Swift
let docsDir = NSSearchPathForDirectoriesInDomains(.documentDirectory, .userDomainMask, true)[0]
let file = docsDir.appending("/outFile.aif")
let csdPath = Bundle.main.path(forResource: "csdFile", ofType: "csd")
csound.record(csdPath, toFile: file)
These demonstrations above save the audio files in the app’s documents directory, which allows write access for file and subdirectory storage on iOS. Note that the -W and -A flags behave as usual on iOS: they will decide whether the file rendered is a WAV or an AIFF file. In the event that neither is provided, the latter will be used as a default.
4 The CsoundUI Class
The CsoundUI class provides for direct bindings between named Csound channels and commonly used objects from the UIKit iOS framework. While it is not necessary to use a CsoundUI object for this communication between iOS and Csound, it can, in many cases, abstract the process of setting up a UI object binding to a single line of code. To initialize a CsoundUI object, we must give it a reference to our Csound object:
//Objective-C
CsoundUI *csoundUI = [[CsoundUI alloc] initWithCsoundObj: self.csound];
// Swift
var csoundUI = CsoundUI(csoundObj: csound)
Normally, however, these objects are declared as properties rather than locally in methods. As mentioned, CsoundUI uses named channels for communicating to and from Csound. Once set-up, values passed to these named channels are normally accessed through the chnget opcode, for example:
instr 1
kfreq chnget " frequency "
asig oscil 0.5 , kfreq
outs asig , asig
endin
Conversely, in order to pass values from Csound, the chnset opcode is normally used with two arguments. The first is the variable, and it is followed by the channel name:
instr 1
krand randomi 300 , 2000 , 1 , 3
asig poscil 0.5 , krand
outs asig , asig
chnset krand , " randFreq "
endin
4.1 UIButton Binding
The UIButton binding is predominantly contained within the CsoundButtonBinding class, which CsoundUI uses to create individual button bindings. To add a button binding, use:
//Objective-C
[self.csoundUI addButton:self.button forChannelName:"channelName"];
// Swift
csoundUI.add(button, forChannelName: "channelName")
Where self.button is the button you would like to bind to, and the string "channelName" contains the name of the channel referenced by chnget in Csound.
The corresponding value in Csound will be equal to 1 while the button is touched, and reset to 0 when it is released. A simple example of how this might be used in Csound, based on the pvscross example by Joachim Heintz, is shown below:
instr 1
kpermut chnget " crossToggle "
ain1 soundin " fox .wav"
ain2 soundin " wave .wav"
;fft - analysis of file 1
fftin1 pvsanal ain1 , 1024 , 256 , 1024 , 1
;fft - analysis of file 2
fftin2 pvsanal ain2 , 1024 , 256 , 1024 , 1
if kpermut == 1 then
fcross pvscross fftin2 , fftin1 , .5 , .5
else
fcross pvscross fftin1 , fftin2 , .5 , .5
endif
aout pvsynth fcross
out aout
endin
4.2 UISwitch Binding
The UISwitch binding provides a connection between the UISwitch object and a named channel in Csound. This binding is managed in the CsoundSwitchBinding class and you can create a UISwitch binding by using:
//Objective-C
[self.csoundUI addSwitch:self.uiSwitch forChannelName:"channelName"];
// Swift
csoundUI.add(switch, forChannelName: "channelName")
As in the case of the UIButton binding, the UISwitch binding provides an on-off state value (1 or 0 respectively) to Csound. Below we use it to turn on or off a simple note generator:
; Triggering instrument
instr 1
kTrigFreq randomi gkTrigFreqMin , gkTrigFreqMax , 5
ktrigger metro kTrigFreq
kdur randomh .1 , 2 , 5
konoff chnget " instrToggle "
if konoff == 1 then
schedkwhen ktrigger , 0 , 0 , 2 , 0 , kdur
endif
endin
; Sound generating instrument
instr 2
iamp random 0.03 ,0.5
ipan random 0 , 1
ipdx random 0 ,13
ipch table ipdx , 2+i( gkscale )
aenv expseg 1 , ( p3 ) , .001
asig oscil iamp * aenv , cpspch(ipch) , 1
outs asig * ipan , asig * (1 - ipan)
endin
4.3 UILabel Binding
The UILabel binding allows you to display any value from Csound in a UILabel object. This can often be a helpful way of providing feedback to the user. You can add a label binding with:
//Objective-C
[self.csoundUI addLabel:self.label forChannelName:"channelName"];
// Swift
csoundUI.add(label, forChannelName: "channelName")
However, in this case the channel is an output channel. To demonstrate, let us add an output channel in Csound to display the frequency of the sound generating instrument’s oscillator from the previous example (for UISwitch):
; Triggering instrument
instr 1
kTrigFreq randomi gkTrigFreqMin , gkTrigFreqMax , 5
ktrigger metro kTrigFreq
kdur randomh .1 , 2 , 5
konoff chnget " instrToggle "
if konoff == 1 then
schedkwhen ktrigger , 0 , 0 , 2 , 0 , kdur
endif
endin
; Sound generating instrument
instr 2
iamp random 0.03 ,0.5
ipan random 0 , 1
ipdx random 0 ,13
ipch table ipdx , 2+i( gkscale )
aenv expseg 1 , ( p3 ) , .001
asig oscil iamp * aenv , cpspch(ipch) , 1
chnset cpspch(ipch) , " pitchOut "
outs asig * ipan , asig * (1 - ipan)
endin
Note additionally that the desired precision of the value display can be set beforehand using the labelPrecision property of the CsoundUI object. For example:
self.csoundUI.labelPrecision = 4;
4.4 UISlider Binding
The UISlider binding is possibly the most commonly used UI binding - it allows the value of a UISlider object to be passed to Csound whenever it changes. This is set up in the CsoundSliderBinding class and we access it via CsoundUI using:
// Objective-C
[self.csoundUI addSlider:self.slider
forChannelName:"channelName"];
// Swift
csoundUI.add(slider, forChannelName: "channelName")
Note that this restricts you to using the slider’s actual value, rather than a rounded verion of it or some other variation, which would normally be best suited to a manual value binding, which is addressed later in this guide. An example is provided below of two simple such UISlider-bound values in Csound:
sr = 44100
ksmps = 128
nchnls = 2
0dbfs = 1
instr 1
kfreq chnget " frequency " ; input 0 - 1
kfreq expcurve kfreq , 500 ; exponential distribution
kfreq *= 19980 ; scale to range
kfreq += 20 ;add offset
kamp chnget " amplitude "
kamp port kamp , .001 ; smooth values
asig poscil kamp , kfreq
outs asig , asig
endin
Above we get ’around’ being restricted to the value of the UISlider by creating an exponential distribution in Csound. Of course we could simply make the minimum and maximum values of the UISlider 20 and 20000 respectively, but that would be a linear distribution by default. In both cases here, the UISlider’s range of floating point values is set to be from 0 to 1.
4.5 Momentary Button Binding
The momentary button binding is similar to the normal UIButton binding in that it uses a UIButton, however it differs in how it uses this object. The UIButton binding passes a channel value of 1 for as long as the UIButton is held, whereas the momentary button binding sets the channel value to 1 for one Csound k-period (i.e. one k-rate sample). It does this by setting an intermediate value to 1 when the button is touched, passing this to Csound on the next k-cycle, and immediately resetting it to 0 after passing it. This is all occurring predominantly in the CsoundMomentaryButtonBinding class, which we access using:
// Objective-C
[self.csoundUI addMomentaryButton:self.triggerButton forChannelName:"channelName"];
// Swift
csoundUI.addMomentaryButton(triggerButton, forChannelName: "channelName")
Here’s a simple usage example:
; Triggering instrument
instr 1
ktrigger chnget " noteTrigger "
schedkwhen ktrigger , 0 , 0 , 2 , 0 , kdur
endin
; Sound generating instrument
instr 2
iamp random 0.03 ,0.5
ipan random 0 , 1
ipdx random 0 ,13
ipch table ipdx , 2+i( gkscale )
aenv expseg 1 , ( p3 ) , .001
asig oscil iamp * aenv , cpspch(ipch) , 1
chnset cpspch(ipch) , " pitchOut "
outs asig * ipan , asig * (1 - ipan)
endin
This replaces the automatic instrument triggering with a manual trigger. Every time the UIButton is touched, a note (by way of an instance of instr 2) will be triggered. This may seem like a more esoteric binding, but there are a variety of potential uses.
5 The CsoundMotion Class
The CsoundMotion class and its associated bindings allow information to be passed from a device’s motion sensors, via the CoreMotion framework, to Csound. As with CsoundUI, it is possible to pass this data indirectly by writing code to mediate between CoreMotion and Csound, but CsoundMotion simplifies and greatly abstracts this process. Subsection 4.4 shows an example of how these values are accessed and might be used in Csound. Note that with CsoundMotion, you do not assign channel names: they are pre-assigned by the relevant objects (e.g. "AccelerometerX").
To declare and initialize a CsoundMotion object, use:
// Objective-C
CsoundMotion *csoundMotion = [[CsoundMotion alloc] initWithCsoundObj:self.csound];
// Swift
var csoundMotion = CsoundMotion(csoundObj: csound)
As with CsoundUI, it may often be advantageous to declare the CsoundMotion object as a property rather than locally.
5.1 Accelerometer Binding
The acclerometer binding, implemented in the CsoundAccelerometerBinding class and enabled through the CsoundMotion class, allows access to an iOS device’s accelerometer data along its three axes (X, Y, Z). The accelerometer is a device that measures acceleration, aiding in several basic interactions. To enable it, use:
// Objective-C
[csoundMotion enableAccelerometer];
// Swift
csoundMotion.enableAccelerometer()
5.2 Gyroscope Binding
The gyroscope binding, implemented in the CsoundGyroscopeBinding class and enabled through the CsoundMotion class, allows access to an iOS device’s gyroscope data along its three axes (X, Y, Z). The accelerometer is a device that allows rotational velocity to be determined, and together with the accelerometer forms a system with six degrees of freedom. To enable it, use:
// Objective-C
[csoundMotion enableGyroscope];
// Swift
csoundMotion.enableGyroscope()
5.3 Attitude Binding
Finally, the attitude binding, implemented in CsoundAttitudeBinding and enabled through CsoundMotion, allows access to an iOS device’s ’attitude data’. As the Apple reference notes, ’attitude’ refers to the orientation of a body relative to a given frame of reference. CsoundMotion enables this as three Euler angle valies: ’roll’, ’pitch’, and ’yaw’ (rotation around X, Y, and Z respectively). To enable the attitude binding, use:
// Objective-C
[csoundMotion enableAttitude];
// Swift
csoundMotion.enableAttitude()
Together, these bindings enable control of Csound parameters with device motion in ways that are very simple and straightforward. In the following subsection, an example demonstrating each of the pre-set channel names as well as how some of this information might be used is provided.
5.4 Motion Csound Example
Here is an example of a Csound instrument that accesses all of the data, and demonstrates uses for some of it. This example is taken from the Csound for iOS Examples project.
instr 1
kaccelX chnget " accelerometerX "
kaccelY chnget " accelerometerY "
kaccelZ chnget " accelerometerZ "
kgyroX chnget " gyroX "
kgyroY chnget " gyroY "
kgyroZ chnget " gyroZ "
kattRoll chnget " attitudeRoll "
kattPitch chnget " attitudePitch "
kattYaw chnget " attitudeYaw "
kcutoff = 5000 + (4000 * kattYaw )
kresonance = .3 + (.3 * kattRoll )
kpch = 880 + ( kaccelX * 220)
a1 vco2 ( kattPitch + .5) * .2 , kpch
a1 moogladder a1 , kcutoff , kresonance
aL , aR reverbsc a1 , a1 , .72 , 5000
outs aL , aR
endin
Each of the channel names is shown here, and each corresponds to what is automatically set in the relevant binding. A little experimenting can be very helpful in determining what to use these values for in your particular application, and of course one is never under any obligation to use all of them. Regardless, they can be helpful and very straightforward ways to add now-familiar interactions.
6 The CsoundBinding Protocol
The CsoundBinding protocol allows you to read values from and write values to Csound using named channels that can be referenced in your .csd file using opcodes like chnget and chnset, as described in the earlier section on CsoundUI. The protocol definition from CsoundObj is:
@protocol CsoundBinding <NSObject>
- (void)setup:(CsoundObj*)csoundObj;
@optional
- (void)cleanup;
- (void)updateValuesFromCsound;
- (void)updateValuesToCsound;
@end
In order to add a binding object to Csound, use CsoundObj’s addBinding method:
// Objective-C
[self.csound addBinding:self];
// Swift
csound.addBinding(self)
Note that you will need to conform to the CsoundBinding protocol, and implement. at minimum, the required setup method. The CsoundBinding setup method will be called on every object added as a binding, and the remaining methods, marked with the @optional directive will be called on any bindings that implement them.
6.1 Channels and Channel Types
Named channels allow us to pass data to and from Csound while it is running. These channels refer to memory locations that we can write to and Csound can read from, and vice-versa. The two most common channel types are: CSOUND_CONTROL_CHANNEL refers to a floating point control channel, normally associated with a k-rate variable in Csound. CSOUND_AUDIO_CHANNEL refers to an array of floating point audio samples of length ksmps.
Each of these can be an input or output channel depending on whether values are being passed to or from Csound.
Given below is an example of using named channels in a simplified Csound instrument. The polymorphic chnget and chnset opcodes are used, and the context here implies that kverb received its value from an input control channel named "verbMix", and that asig outputs to an audio channel named "samples".
giSqr ftgen 2 , 0 , 8192 , 10 , 1 , 0 , .33 , 0 , .2 , 0 , .14 , 0 , .11 , 0 , .09
instr 1
kfreq = p4
kverb chnget " verbMix "
aosc poscil .5 , kfreq , 2
arvb reverb aosc , 1.5
asig = (aosc * (1 - kverb) ) + (arvb * kverb)
chnset asig , " samples "
outs asig , asig
endin
The section that follows will describe how to set up and pass values to and from this instrument’s channels in an iOS application.
6.2 The Setup Method
The setup method is called before Csound’s first performance pass, and this is typically where channel references are created. For example:
// Objective-C
// verbPtr and samplesPtr are instance variables of type float*
-(void)setup:(CsoundObj *)csoundObj {
verbPtr = [csoundObj getInputChannelPtr:@"verbMix" channelType:CSOUND_CONTROL_CHANNEL];
samplesPtr = [csoundObj getOutputChannelPtr:@"samples" channelType:CSOUND_AUDIO_CHANNEL];
}
// Swift
var verbPtr: UnsafeMutablePointer<Float>?
var samplesPtr: UnsafeMutablePointer<Float>?
func setup(_ csoundObj: CsoundObj) {
verbPtr = csoundObj.getInputChannelPtr("verbMix", channelType: CSOUND_CONTROL_CHANNEL)
samplesPtr = csoundObj.getOutputChannelPtr("samples", channelType: CSOUND_AUDIO_CHANNEL)
}
The cleanup method from CsoundBinding, also optional, is intended for use in removing bindings once they are no longer active. This can be done using CsoundObj’s removeBinding method:
// Objective-C
// verbPtr and samplesPtr are instance variables of type float*
-(void)cleanup {
[self.csound removeBinding:self];
}
// Swift
func cleanup() {
csound.removeBinding(self)
}
6.3 Communicating Values To and From Csound
Communicating values to Csound is normally handled in the updateValuesToCsound method. This method is called once per performance pass (i.e. at the k-rate). For example:
// Objective-C
-(void)updateValuesToCsound {
*verbPtr = self.verbSlider.value;
}
// Swift
func updateValuesToCsound() {
verbPtr?.pointee = verbSlider.value
}
This updates the value at a memory location that Csound has already associated with a named channel (in the setup method). This process has essentially replicated the functionality of the CsoundUI API’s slider binding. The advantage here is that we could perform any transformation on the slider value, or associate another value (that might not be associated with a UI object) with the channel altogether. To pass values back from Csound, we use the updateValuesFromCsound method.
// Objective-C
-(void)updateValuesFromCsound {
float *samps = samplesPtr;
}
Note that in Swift, we have do a little extra work in order to get an array of samples that we can easily index into:
// Swift
func updateValuesFromCsound() {
let samps = samplesPtr?.pointee
let sampsArray = [Float](UnsafeBufferPointer(start: audioPtr,
count: Int(csound.getKsmps())))
}
Note also that updateValuesToCsound is called before updateValuesFromCsound during each performance pass, with the Csound engine performance call in between the two.
7 The CsoundObjListener Protocol
The CsoundObjListener protocol allows objects in your program to be notified when Csound begins running, and when it completes running. The protocol definition from CsoundObj is:
@protocol CsoundObjListener <NSObject>
@optional
- (void)csoundObjStarted:(CsoundObj *)csoundObj;
- (void)csoundObjCompleted:(CsoundObj *)csoundObj;
@end
Note that there are no methods that an object is required to adopt in order to conform to this protocol. These methods simply allow an object to elect to be notified when Csound either begins, completes running, or both. Note that these methods are not called on the main thread, so any UI work must be explicitly run on the main thread. For example:
// Objective-C
-(void)viewDidLoad {
[super viewDidLoad];
[self.csound addListener:self];
}
- (void)csoundObjStarted:(CsoundObj *)csoundObj {
[self.runningLabel performSelectorOnMainThread:@selector(setText:) withObject:@"Csound Running" waitUntilDone:NO];
}
// Swift
override func viewDidLoad() {
super.viewDidLoad()
csound.add(self)
}
func csoundObjCompleted(_ csoundObj: CsoundObj) {
DispatchQueue.main.async { [unowned self] in
self.runningLabel.text = "Csound Stopped"
}
}
8 Console Output
Console output from Csound is handled via a callback. You can set the method that handles console info using CsoundObj’s setMessageCallbackSelector method, and passing in an appropriate selector, for instance:
// Objective-C
[self.csound setMessageCallbackSelector:@selector(printMessage:)];
// Swift
csound.setMessageCallbackSelector(#selector(printMessage(_:)))
An object of type NSValue will be passed in. This object is acting as a wrapper for a C struct of type Message. The definition for Message in CsoundObj.h is:
typedef struct {
CSOUND *cs;
int attr;
const char *format;
va_list valist;
} Message;
The two fields of interest to us for the purposes of console output are format and valist. The former is a format string, and the latter represents a list of arguments to match its format specifiers.
The process demonstrated in the code examples below can be described as:
- Declare an instance of a Message struct.
- Unwrap the NSValue to store its contained Message value at the address of this instance.
- Declare an empty C string, to act as a buffer.
- Use the vsnprintf function to populate the buffer with the formatted output string.
- Wrap this C string in an Objective-C NSString or Swift String.
// Objective-C
- (void)printMessage:(NSValue *)infoObj
Message info;
[infoObj getValue:&info];
char message[1024];
vsnprintf(message, 1024, info.format, info.valist);
NSString *messageStr = [NSString stringWithFormat:@"%s", message];
NSLog(@"%@", messageStr);
}
Note that in Swift, we have to create a CVaListPointer (equivalent to a va_list* in C) for use with the vsnprintf() function:
// Swift
func messageCallback(_ infoObj: NSValue) {
var info = Message()
infoObj.getValue(&info)
let message = UnsafeMutablePointer<Int8>.allocate(capacity: 1024)
let va_ptr: CVaListPointer = CVaListPointer(_fromUnsafeMutablePointer: &(info.valist))
vsnprintf(message, 1024, info.format, va_ptr)
let messageStr = String(cString: message)
print(messageStr)
}
In both cases above, we are printing the resulting string objects to Xcode’s console. This can be very useful for finding and addressing issues that have to do with Csound or with a .csd file you might be using.
We could also pass the resulting string object around in our program; for example, we could insert the contents of this string object into a UITextView for a simulated Csound console output.
9 Csound-iOS and MIDI
9.1 CsoundObj and MIDI
The Csound iOS API provides two possible ways of passing MIDI information to Csound. CsoundObj can receive MIDI events from CoreMIDI directly. By default, this functionality is disabled, but setting CsoundObj’s midiInEnabled property to true (or YES on Objective-C) enables it. This must, however be done before Csound is run.
Note that you must also set the appropriate command-line flag in your csd, under CsOptions. For example, -M0. Additionally, the MIDI device must be connected before the application is started.
9.2 MidiWidgetsManager
The second way that is provided to communicate MIDI information to Csound is indirect, via the use of UI widgets and CsoundUI. In this case, the MidiWidgetsManager uses a MidiWidgetsWrapper to connect a MIDI CC to a UI object, and then CsoundUI can be used to connect this UI object’s value to a named channel in Csound. For instance:
// Objective-C
MidiWidgetsManager *widgetsManager = [[MidiWidgetsManager alloc] init];
[widgetsManager addSlider:self.cutoffSlider forControllerNumber:5];
[csoundUI addSlider:self.cutoffSlider forChannelName:@"cutoff"];
[widgetsManager openMidiIn];
// Swift
let widgetsManager = MidiWidgetsManager()
widgetsManager.add(cutoffSlider, forControllerNumber: 5)
csoundUI?.add(cutoffSlider, forChannelName: "cutoff")
widgetsManager.openMidiIn()
An advantage of this variant is that MIDI connections to the UI widgets are active even when Csound is not running, so visual feedback can still be provided, for example. At the time of writing, support is only built-in for UISliders.
10 Other Functionality
This section describes a few methods of CsoundObj that are potentially helpful for more complex applications.
10.1 getCsound
(CSOUND *)getCsound;
The getCsound method returns a pointer to a struct of type CSOUND, the underlying Csound instance in the C API that the iOS API wraps. Because the iOS API only wraps the most commonly needed functionality from the Csound C API, this method can be helpful for accessing it directly without needing to modify the Csound iOS API to do so.
Note that this returns an opaque pointer because the declaration of this struct type is not directly accessible. This should, however, still allow you to pass it into Csound C API functions in either Objective-C or Swift if you would like to access them.
10.2 getAudioUnit
(AudioUnit *)getAudioUnit;
The getAudioUnit method returns a pointer to a CsoundObj instance’s I/O AudioUnit, which provides audio input and output to Csound from iOS.
This can have several potential purposes. As a simple example, you can use the AudioOutputUnitStop() function with the returned value’s pointee to pause rendering, and AudioOutputUnitStart() to resume.
10.3 updateOrchestra
(void)updateOrchestra:(NSString *)orchestraString;
The updateOrchestra method allows you to supply a new Csound orchestra as a string.
10.4 Other
Additionally, getKsmps returns the current ksmps value, and getNumChannels returns the number of audio channels in use by the current Csound instance. These both act directly as wrappers to Csound C API functions.
11 Example Projects
The Csound iOS examples project, available in both Objective-C and Swift, is a collection of code that demonstrates common uses of and interactions with the Csound iOS API.
For documentation on the examples, refer to the Csound-iOS reference manual (Yi, Lazzarini, Boulanger), included with the API and examples.
11.1 csoundSynthesizer
csoundSynthesizer is a separate project that demonstrates building a small, simple iOS application that is usable as a rudimentary synthesizer. It is not intended to be an exhaustive reference, for which purpose the Csound iOS Examples projects are better suited, but to help a new user get up and running with Csound on iOS. The project is available in both Swift and Objective-C here.
12 Conclusion
This guide provides an outline of the Csound iOS API’s functionality, and demonstrates some common applications of it, in order to aid those who have acquired even some background in Csound to develop powerful audio applications without worrying about the low-level intricacies of Apple’s Core Audio.
We wish you all the best as you continue your journey into developing apps with the power and possibilities Csound has to offer.
F. CSOUND ON ANDROID
Introduction
Now that we have spent some time with Csound on Android, we have come to realize that a high end smartphone, not to mention a tablet, is in every sense of the word a real computer. The limits to what can be programmed on it are indefinable. On a high-end personal computer, it is easier to type, and Csound runs quite a bit faster; but there is no essential difference between running Csound on a computer and running it on a smartphone.
Csound has been available on the Android platform since 2012 (Csound 5.19), thanks to the work of Victor Lazzarini and Steven Yi. Csound 6 was ported to Android, and enhanced, by Michael Gogins and Steven Yi in the summer of 2013. This chapter is about Csound 6 for Android, or just Csound for Android.
The following packages are available for Android:
- The CsoundAndroid library, which is intended to be used by developers for creating apps based on Csound.
- The Csound6 app, which is a self-contained environment for creating, editing, debugging, and performing Csound pieces on Android. (It used to be called the CSDPlayer, but has since been enhanced to support editing and other features.) The app includes a number of built-in example pieces.
These packages are available for download from the SourceForge site's file pages at http://sourceforge.net/projects/csound/files/csound6/.
For more information about these packages, download them and consult the documentation contained therein.
The Csound6 app
The Csound6 app (or Csound for Android) permits the user, on any Android device that is powerful enough, including most tablets and the most powerful smartphones, to do most things that can be done with Csound on any other platform such as OS X, Windows, or Linux. This includes creating Csound pieces, editing them, debugging them, and performing them, either in real time to audio output or to a soundfile for later playback.
The app has a built-in, pre-configured user interface with five sliders, five push buttons, one trackpad, and a 3 dimensional accelerometer that are pre-assigned to control channels which can be read using Csound's chnget opcode.
The app also contains an embedded Web browser, based on WebKit, that can parse, interpret, and present HTML and JavaScript code that is contained in the <html> element of the CSD file. The embedded browser implements most features of the HTML5 standard. Selected commonly used functions from the Csound API are available from JavaScript embedded in this <html> code, and can be used to control Csound from HTML user interfaces, generate scores, and do many other things. For a more complete introduction to the use of HTML with Csound, see Chapter 12, Section H, Csound and HTML. On Android, if the <html> element is present in the CSD file, the built-in widgets will be replaced by a Web page that will be constructed from the code in the <html> element of the CSD.
The app also has some limitations and missing features compared with the longer-established platforms. These include:
- There is no real-time MIDI input or output.
- Audio input is not accurately synchronized with audio output.
- Many plugin opcodes are missing, including most opcodes involved with using other plugin formats or inter-process communications.
However, some of the more useful plugins are indeed available on Android:
- The signal flow graph opcodes for routing audio from instruments to effects, etc.
- The FluidSynth opcodes for playing SoundFonts.
- The Lua opcodes for running Lua code in Csound and even defining new Csound opcodes in Lua.
- The Open Sound Control (OSC) opcodes.
- The libstdutil library, which enables Csound to be used for various time/frequency analysis and resynthesis tasks, and for other purposes.
Installing the App
There are two ways to install the Csound6 app. You can download it using your device, or you can download it to a computer and transfer it to your device. These methods are presented below.
Preparing Your Device
Using the Csound6 app is similar to using an application on a regular computer. You need to be able to browse the file system, and you need to be able to edit csd files.
There are a number of free and paid apps that give users the ability to browse the Linux file system that exists on all Android devices. If you don't already have such a utility, you should install a file browser that provides access to as much as possible of the file system on your device, including system storage and external store such as an SD card. I have found that the free AndroZip app can do this.
There also is an increasing number of free and paid text editors for Android. The one that I chose to use for developing, testing, and using the Csound6 app is the free version of the Jota text editor. There are also various enhanced paid versions of this app, and of course you may find some other editor more suitable to your purposes. Other editors should also be able to work with Csound, although they have only very lightly been tested.
When you use Csound, the command for editing csd files will transparently invoke the editor, as though it was an integral part of the app. This kind of integration is an appealing feature of the Android operating system.
If you render soundfiles, they take up a lot of space. For example, CD-quality stereo soundfiles (44.1 KHz, 16 bit) take up about 10 megabytes per minute of sound. Higher quality or more channels take up even more room. But even without extra storage, a modern smartphone should have gigabytes, thousands of megabytes, of free storage. This is actually enough to make an entire album of pieces.
On most devices, installing extra storage is easy and not very expensive. I recommend obtaining the largest possible SD card, if your device supports them. This will vastly expand the amount of available space, up to 32 or 64 gigabytes or even more.
Download to Device
To download the Csound6 app to your device, go online using Google Search or a Web browser. You can find the application package file, Csound6.apk, on SourceForge, on the Csound project site, on the File page (you may first have to allow your android to install an app which is not in Google Play). The app will be on one of the more recent releases of Csound 6. For example, you can find it at Csound6.apk. But you should look for the latest release and use that.
Click on the filename to download the package. The download will happen in the background. You can then go to the notifications bar of your device and click on the downloaded file. You will be presented with one or more options for how to install it. The installer will ask for certain permissions, which you need to grant.
Transfer from a Computer
It's also easy to download the Csound6.apk file to a personal computer. Once you have downloaded the file from SourceForge, connect your device to the computer with a USB cable. The file system of the device should then automatically be mounted on the file system of the computer. Find the Csound6.apk in the computer's download directory, and copy the Csound6.apk file. Find your device's download directory, and paste the Csound.apk file there.
Then you will need to use a file browser that is actually on your device, such as AndropZip. Browse to your Download directory, select the Csound6.apk file, and you should be presented with a choice of actions. Select the Install action. The installer will ask for certain permissions, which you should give.
User Interface
New – creates a blank template CSD file in the root directory of the user's storage for the user to edit. The CSD file will be remembered and performed by Csound.
Open – opens an existing CSD file in the root directory of the user's storage. The user's storage filesystem can be navigated to find other files.
Edit – opens a text editor to edit the current CSD file. Be sure to save the file before you perform it! I recommend the free, open source Jota text editor on smartphones and, though I haven't tried Jota on tablets, it probably works well there as well.
Start/Stop – if a CSD file has been loaded, pushing the button starts running Csound; if Csound is running, pushing the button stops Csound. If the <CsOptions> element of the CSD file contains -odac, Csound's audio output will go to the device audio output. If the element contains -osoundfilename, Csound's audio output will go to the file soundfilename, which should be a valid Linux pathname in the user's storage filesystem.
The widgets are assigned control channel names slider1 through slider5, butt1 through butt5, trackpad.x, and trackpad.y. In addition, the accelerometer on the Android device is available as accelerometerX, accelerometerY, and accelerometerZ.
The values of these widgets are normalized between 0 and 1, and can be read into Csound during performance using the chnget opcode, like this:
kslider1_value chnget “slider1”
The area below the trackpad prints messages output by Csound as it runs.
The Settings Menu
The Settings menu on your device offers the following choices:
- Examples contains a number of example pieces that are built in to the app. Selecting an example will load it into Csound for performance or editing.
- User guide links to this chapter of this online manual.
- Csound help links to the online Csound Reference Manual.
- About Csound links to the csounds.com Web site, which acts as a portal for all things concerning Csound.
- Settings opens a dialog for setting environment variables that specify default locations for soundfiles, samples, scores, and so on. In the Csound6 app, these environment variables are configured by Android app settings.
Configuring Default Directories
Run the Csound6 app, invoke the menu button, and choose Settings. You will be given choices for specifying an (additional) Plugins directory, a soundfile Output directory, a Samples directory, an Analysis directory, and an Include directory for score and orchestra files to be #included by a Csound piece.
These settings are not required, but they can make using Csound easier and faster to use.
Loading and Performing a Piece
Example Pieces
From the app's menu, select the Examples command, then select one of the listed examples, for example Xanadu by Joseph Kung. You may then click on the Start button to perform the example, or the Edit button to view the code for the piece. If you want to experiment with the piece, you can use the Save as... button to save a copy on your device's file system under a different name. You can then edit the piece and save your changes.
Running an Existing Piece
If you have access to a mixer and monitor speakers, or even a home stereo system, or even a boom box, you can hook up your device's headphone jack to your sound system with an adapter cable. Most devices have reasonably high quality audio playback capabilities, so this can work quite well.
Just to prove that everything is working, start the Csound app. Go to the app menu, select the Examples item, select the Xanadu example, and it will be loaded into Csound. Then click on the Start button. Its name should change to Stop, and Csound's runtime messages should begin to scroll down the black pane at the bottom of the screen. At the same time, you should hear the piece play. You can stop the performance at any time by selecting the Stop button, or you can let the performance complete on its own.
That's all there is to it. You can scroll up and down in the messages pane if you need to find a particular message, such as an error or warning.
If you want to look at the text of the piece, or edit it, select the Edit button. If you have installed Jota, that editor should open with the text of the piece, which you can save, or not. You can edit the piece with the this editor, and any changes you make and save will be performed the next time you start the piece.
Creating a New Piece
This example will take you through the process of creating a new Csound piece, step by step. Obviously, this piece is not going to reveal anything like the full power of Csound. It is only intended to get you to the point of being able to create, edit, and run a Csound piece that will actually make sound on your Android device – from scratch.
Before you get started, install the Jota text editor on your device. Other text editors might work with the Csound app, but this one is known to work.
Run the Csound6 app...
Select the New button. You should be presented with an input dialog asking you for a filename for your piece. Type in toot.csd, and select the Ok button. The file will be stored in the root directory of your user storage on your device. You can save the file to another place using Jota's File menu, if you like.
The text editor should open with a “template” CSD file. Your job is to fill out this template to hear something.
Create a blank line between <CsOptions> and </CsOptions>, and type -odac -d -m3. This means send audio to the real-time output (-odac), do not display any function tables (-d), and log some informative messages during Csound's performance (-m3).
Create a blank line between <CsInstruments> and </CsInstruments> and type the following text:
sr = 44100
ksmps = 32
nchnls = 1
0dbfs = 1
instr 1
asignal poscil 0.2, 440
out asignal
endin
This is just about the simplest possible Csound orchestra. The orchestra header specifies an audio signal sampling rate of 44,100 frames per second, with 10 audio frames per control signal sample, and one channel of audio output. The instrument is just a simple sine oscillator. It plays a tone at concert A.
Create a blank line between <CsScore> and </CsScore> and type:
i1 0 5
This means play instrument 1 starting at time 0 for 5 seconds.
Select the text editor's Save button and then its Quit button.
Select the Csound app's Start button. You should hear a loud sine tone for 5 seconds.
If you want to save your audio output to a soundfile named test.wav, change -odac above to -o/sdcard/test.wav.
That's it!
Using the Widgets
This chapter shows how to use the built-in widgets of the Csound for Android app for controlling Csound in performance. For instructions on how to use the <html> element of the CSD file to create custom user interfaces, see the "Csound and HTML" chapter of this book.
The Csound for Android app provides access to a set of predefined on-screen widgets, as well as to the accelerometer on the device. All of these controllers are permanently assigned to pre-defined control channels with pre-defined names, and mapped to a pre-defined range of values, from 0 to 1.
All of this pre-definition... this is both good and bad. I have found, following the example of Iain McCurdy who has graciously contributed a number of the examples for the app, an approach that simplifies using the controllers. For an example of this approach in action, look at the source code for the Gogins/Drone-IV.csd example.
You should be able to cut and paste this code into your own pieces without many changes.
The first step is to declare one global variable for each of the control channels, with the same name as the control channel, at the top of the orchestra header, initialized to a value of zero:
gkslider1 init 0
gkslider2 init 0
gkslider3 init 0
gkslider4 init 0
gkslider5 init 0
gkbutt1 init 0
gkbutt2 init 0
gkbutt3 init 0
gkbutt4 init 0
gkbutt5 init 0
gktrackpadx init 0
gktrackpady init 0
gkaccelerometerx init 0
gkaccelerometery init 0
gkaccelerometerz init 0
Then write an "always-on" instrument that reads each of these control channels into each of those global variables. At the top of the orchestra header:
alwayson "Controls"
As the next to last instrument in your orchestra:
instr Controls
gkslider1 chnget "slider1"
gkslider2 chnget "slider2"
gkslider3 chnget "slider3"
gkslider4 chnget "slider4"
gkslider5 chnget "slider5"
gkbutt1 chnget "butt1"
gkbutt2 chnget "butt2"
gkbutt3 chnget "butt3"
gkbutt4 chnget "butt4"
gkbutt5 chnget "butt5"
gktrackpadx chnget "trackpad.x"
gktrackpady chnget "trackpad.y"
gkaccelerometerx chnget "accelerometerX"
gkaccelerometery chnget "accelerometerY"
gkaccelerometerz chnget "accelerometerZ"
endin
So far, everything is common to all pieces. Now, for each specific piece and specific set of instruments, write another always-on instrument that will map the controller values to the names and ranges required for your actual instruments. This code, in addition, can make use of the peculiar button widgets, which only signal changes of state and do not report continuously whether they are "on" or "off." These examples are from Gogins/Drone-IV.csd.
At the top of the orchestra header:
alwayson "VariablesForControls"
As the very last instrument in your orchestra:
instr VariablesForControls
if gkslider1 > 0 then
gkFirstHarmonic = gkslider1 * 2
gkgrainDensity = gkslider1 * 400
gkratio2 = gkslider1 ;1/3
endif
if gkslider2 > 0 then
gkDistortFactor = gkslider2 * 2
gkgrainDuration = 0.005 + gkslider2 / 2
gkindex1 = gkslider2 * 4
endif
if gkslider3 > 0 then
gkVolume = gkslider3 * 5
gkgrainAmplitudeRange = gkslider3 * 300
gkindex2 = gkslider3 ;0.0125
endif
if gkslider4 > 0 then
gkgrainFrequencyRange = gkslider4 / 10
endif
if gktrackpady > 0 then
gkDelayModulation = gktrackpady * 2
; gkGain = gktrackpady * 2 - 1
endif
if gktrackpadx > 0 then
gkReverbFeedback = (3/4) + (gktrackpadx / 4)
; gkCenterHz = 100 + gktrackpadx * 3000
endif
kbutt1 trigger gkbutt1, .5, 0
if kbutt1 > 0 then
gkbritels = gkbritels / 1.5
gkbritehs = gkbritehs / 1.5
; gkQ = gkQ / 2
endif
kbutt2 trigger gkbutt2, .5, 0
if kbutt2 > 0 then
gkbritels = gkbritels * 1.5
gkbritehs = gkbritehs * 1.5
; gkQ = gkQ * 2
endif
endin
Now, the controllers are re-mapped to sensible ranges, and have names that make sense for your intruments. They can be used as follows. Note particularly that, just above the instrument definition, in other words actually in the orchestra header, these global variables are initialized with values that will work in performance, in case the user does not set up the widgets in appropriate positions before starting Csound. This is necessary because the widgets in the Csound6 app, unlike say the widgets in CsoundQt, do not "remember" their positions and values from performance to performance.
gkratio1 init 1
gkratio2 init 1/3
gkindex1 init 1
gkindex2 init 0.0125
instr Phaser
insno = p1
istart = p2
iduration = p3
ikey = p4
ivelocity = p5
iphase = p6
ipan = p7
iamp = ampdb(ivelocity) * 8
iattack = gioverlap
idecay = gioverlap
isustain = p3 - gioverlap
p3 = iattack + isustain + idecay
kenvelope transeg 0.0, iattack / 2.0, 1.5, iamp / 2.0, iattack / 2.0, -1.5, iamp, isustain, 0.0, iamp, idecay / 2.0, 1.5, iamp / 2.0, idecay / 2.0, -1.5, 0
ihertz = cpsmidinn(ikey)
print insno, istart, iduration, ikey, ihertz, ivelocity, iamp, iphase, ipan
isine ftgenonce 0,0,65536,10,1
khertz = ihertz
ifunction1 = isine
ifunction2 = isine
a1,a2 crosspm gkratio1, gkratio2, gkindex1, gkindex2, khertz, ifunction1, ifunction2
aleft, aright pan2 a1+a2, ipan
adamping linseg 0, 0.03, 1, p3 - 0.1, 1, 0.07, 0
aleft = adamping * aleft * kenvelope
aright = adamping * aright * kenvelope
outleta "outleft", aleft
outleta "outright", aright
endin
CSOUND AND HASKELL
Csound-expression
Csound-expression is a framework for creation of computer music.
It's a Haskell library to make Csound much more friendly.
It generates Csound files out of Haskell code.
With the help of the library we can create our instruments on the fly. A few lines in the interpreter is enough to get the cool sound going out of your speakers. Some of the features of the library are heavily inspired by reactive programming. We can invoke the instruments with event streams. Event streams can be combined in the manner of reactive programming. The GUI-widgets are producing the event streams as a control messages. Moreover with Haskell we get all standard types and functions like lists, maps, trees. It's a great way to organize code and data.
Csound-expression is an open source library. It's available on Hackage (the main base of Haskell projects).
Key principles
Here is an overview of the features and principles:
- Keep it simple and compact.
- Try to hide low level Csound's wiring as much as we can (no ids for ftables, instruments, global variables). The haskell is a modern language with rich set of abstractions. The author tried to keep the Csound primitives as close to the haskell as possible. For example, invocation of the instrument is just an application of the function.
- No distinction between audio and control rates on the type level. Derive all rates from the context. If the user plugs signal to an opcode that expects an audio rate signal the argument is converted to the right rate.
- Less typing, more music. Use short names for all types. Make library so that all expressions can be built without type annotations. Make it simple for the compiler to derive all types. Don't use complex type classes.
- Ensure that output signal is limited by amplitude. Csound can produce signals with HUGE amplitudes. Little typo can damage your ears and your speakers. In generated code all signals are clipped by 0dbfs value. 0dbfs is set to 1. Just as in Pure Data. So 1 is absolute maximum value for amplitude.
- Remove score/instrument barrier. Let instrument play a score within a note and trigger other instruments. Triggering the instrument is just an application of the function. It produces the signal as output which can be used in another instrument and so on.
- Set Csound flags with meaningful (well-typed) values. Derive as much as you can from the context. This principle let's us start for very simple expressions. We can create our audio signal apply the function dac to it and we are ready to hear the result in the speakers. No need for XML copy and paste form. It's as easy as typing the line ~~~haskell
> dac (osc 440)
~~~
in the interpreter. - The standard functions for musical needs. We often need standard waveforms and filters and adsrs. Some functions are not so easy to use in the Csound. So there are a lot of predefined functions that capture lots of musical ideas. the library strives to defines audio DSP primitives in the most basic easiest form.
- There are audio waves: osc, saw, tri, sqr, pw, ramp, and their unipolar friends (usefull for LFOs).
- There are filters: lp, hp, bp, br, mlp (moog low pass), filt (for packing several filters in chain), formant filters with ppredefined vowels.
- There are handy envelopes: fades, fadeOut, fadeIn, linseg (with held last value).
- There noisy functions: white, pink.
- There are step sequencers: sqrSeq, sawSeq, adsrSeq, and many more. Step sequencer can produce the sequence of unipolar shapes for a given wave-form. The scale factors are defined as the list of values.
- Composable GUIs. Interactive instruments should be easy to make. The GUI widget is a container for signal. It carries an output alongside with visual representation. There are standard ways of composition for the visuals (like horizontal or vertical grouping). It gives us the easy way to combine GUIs. That's how we can create a filtered saw-tooth that is controlled with sliders:
~~~haskell
> dac $ vlift2 (\cps q -> mlp (100 + 5000 * cps) q (saw 110)) (uslider 0.5) (uslider 0.5)
~~~
The function `uslider` produces slider which outputs a unipolar signal (ranges from 0 to 1). The single argument is an initial value. The function vlift2 groups visuals vertically and applies a function of two arguments to the outputs of the sliders. This way we get a new widget that produces the filtered sawtooth wave and contains two sliders. It can become a part of another expression. No need for separate declarations. - Event streams inspired with FRP (functional reactive programming). Event stream can produce values over time. It can be a metronome click or a push of the button, switch of the toggle button and so on. We have rich set of functions to combine events. We can map over events and filter the stream of events, we can merge two streams, accumulate the result.
That's how we can count the number of clicks:
~~~
let clicks = lift1 (\evt -> appendE (0 :: D) (+) $ fmap (const 1) evt) $ button "Click me!"
~~~ - There is a library that greatly simplifies the creation of the music that is based on samples. It's called csound-sampler. With it we can easily create patterns out of wav-files, we can reverse files or play random segments of files.
- There is a novel model for composition predefined in the library. It's based on the assumption that we can delay a signal with an event stream and stop it with an event stream. There is a tiny set of primitives:
~~~haskell
toSeg -- creates a segment out of the signal (it lasts indefinitely)
slim -- limits a segment by an event stream (the segment lasts and waits for the first
event in the event stream to stop itself)
sflow -- it plays a list of segments on after another
spar -- it plays a list of segments at the same time
sloop -- it plays a segment over and over again.
~~~ - With the library we can create our own libraries. We can create a palette of instruments and use it as a library. It means we can just import the instruments o need for copy and paste and worry for collision of names while pasting. In fact there is a library on hackage that is called csound-catalog. It defines some instruments from the Csound Catalog.
Links
The library homepage on hackage: http://hackage.haskell.org/package/csound-expression
The library homepage on github: http://github.com/anton-k/csound-expression/blob/master/tutorial/Index.md
The csound-sampler library: http://github.com/anton-k/csound-sampler
The csound-catalog library homepage on hackage: http://hackage.haskell.org/package/csound-catalog
Music made with Haskell and Csound: http://soundcloud.com/anton-kho
H. CSOUND AND HTML
Introduction
Certain Csound front ends, currently including CsoundQt and Csound for Android, have the ability to use HTML to define user interfaces, to control Csound, and to generate Csound scores and even orchestras. The HTML code is embedded in the optional <html> element of the Csound Structured Data (CSD) file. This element essentially defines a Web page that contains Csound.
This chapter is organized as follows:
- Introduction (this section)
- Installation
- Tutorial User's Guide
- Conclusion
HTML must be understood here to represent not only Hyper Text Markup Language, but also all of the other Web standards that currently are supported by Web browsers, Web servers, and the Internet, including cascading style sheets (CSS), HTML5 features such as drawing on a graphics canvas visible in the page, producing animated 3-dimensional graphics with WebGL including shaders and GPU acceleration, Web Audio, various forms of local data storage, Web Sockets, and so on and so on. This whole conglomeration of standards is currently defined and maintained under the non-governmental leadership of the World Wide Web Consortium (W3C) which in turn is primarily driven by commercial interests belonging to the Web Hypertext Application Technology Working Group (WHATWG). Most modern Web browsers implement almost all of the W3C standards up to and including HTML5 at an impressive level of performance and consistency. To see what features are available in your own Web browser, go to this test page. All of this stuff is now usable in Csound pieces....
Examples of Use
For an example of a few of the things are possible with HTML in Csound, take a look at the following screen shots. Both of these examples are included in the Windows installer for Csound, which also includes the HTML-enabled version of CsoundQt.
 Figure 1. GameOfLife3d.csd.
Figure 1. GameOfLife3d.csd.
In Figure 1, GameOfLife3d.csd demonstrates the following features of HTML: style sheets for formatting the legend, WebGL for displaying a rotating 3-dimensional form of John Conway's Game of Life with shifting lighting, animation which "tweens" the cubes from one state of the game to the next, and the Csound API. The JavaScript code that generates the display also builds up a chunk of Csound score that is sent to Csound. Thus, each new state of the game plays a chord using Csound instruments. The user can interact with the game, rotating it and zooming it.
 Figure 2. LindenmayerCanvas.csd.
Figure 2. LindenmayerCanvas.csd.
In Figure 2, LindenmayerCanvas.csd, the HTML code is used to do these things:
- Define slider widgets for controlling Csound with the channel API, using HTML input elements with JavaScript event handlers.
- Style the sliders and the table containing them with a Custom Style Sheet (CSS).
- Save the positions of the widgets when the 'Save control values' button is clicked, and restore the positions of the widgets when the 'Restore control values' button is clicked, using the Local Storage feature of HTML5. These values are retrieved whenever the piece is loaded.
- Use JavaScript to define a context-free Lindenmayer system for generating not only the tree image drawn on the HTML Canvas at the bottom of the screen, but also a Csound score representing the tree, when the 'Generate score' button is clicked. Being able to see some sort of graphical representation of a score is very useful when doing algorithmic composition.
It is true that LaTeX can do a better job of typesetting than HTML and CSS. It is true that game engines can do a better job for interactive, 3-dimensional computer animation with scene graphs than WebGL. It is true that compiled C or C++ code runs faster than JavaScript. It is true that Haskell is a more fully-featured functional programming language than JavaScript. It is true that MySQL is a more powerful database than HTML5 storage.
But the fact is, there is no single program except for a Web browser that manages to be quite functional in all of these categories in a way that beginning to intermediate programmers can use, and for which the only required runtime is the Web browser itself.
For this reason alone, HTML makes a very good front end for Csound. Furthermore, the Web standards are maintained in a stable form by a large community of competent developers representing diverse interests. So I believe HTML as a front end for Csound should be quite stable and remain backwardly compatible, just as Csound itself remains backwardly compatible with old pieces.
How it Works
The Web browser embedded into CsoundQt is the Chromium Embedded Framework. The Web browser embedded into Csound for Android is the WebView available in the Android SDK.
The front end parses the <html> element out of the CSD file and simply saves it as an HTML file, in other words, as a Web page. For example, MyCsoundPiece.csd will produce MyCsoundPiece.csd.html. The front end's embedded browser then loads this Web page, compiles it, displays it, executes any scripts contained in it, and lets the user interact with it.
It is important to understand that any valid HTML code can be used in Csound's <html> element. It is just a Web page like any other Web page.
In general, the different Web standards are either defined as JavaScript classes and libraries, or glued together using JavaScript. In other words, HTML without JavaScript is dead, but HTML with JavaScript handlers for HTML events and attached to the document elements in the HTML code, comes alive. Indeed, JavaScript can itself define HTML documents by programmatically creating Document Object Model objects.
JavaScript is the engine and the major programming language of the World Wide Web in general, and of code that runs in Web browsers in particular. JavaScript is a standardized language, and it is a functional programming language not that dissimilar in concept from Scheme. JavaScript also allows classes to be defined by prototypes.
The JavaScript execution context of a Csound Web page contains Csound itself as a "csound" JavaScript object that has the following methods:
getVersion() [returns a number]
compileOrc(orchestra_code)evalCode(orchestra_code) [returns the numeric result of the evaluation]
readScore(score_lines)
setControlChannel(channel_name,number)
getControlChannel(channel_name) [returns a number representing the channel value]
message(text)
getSr() [returns a number]
getKsmps() [returns a number]
getNchnls() [returns a number]
isPlaying() [returns 1 if Csound is playing, 0 if not]
The front end contains a mechanism for forwarding JavaScript calls in the Web page's JavaScript context to native functions that are defined in the front end, which passes them on to Csound. This involves a small amount of C++ glue code that the user does not need to know about. In CsoundQt, the glue code uses asynchronous IPC because the Chromium Embedded Framework forks several threads or even processes to implement the Web browser, but again, the user does not need to know anything about this.
In the future, more functions from the Csound API will be added to this JavaScript interface, including, at least in some front ends, the ability for Csound to appear as a Node in a Web Audio graph (this already is possible in the Emscripten built of Csound).
Also in the future, the JavaScript methods of Csound in Emscripten will be harmonized with these methods.
Also in the future, there will be a native Node extension for the NW.js HTML5 desktop application framework, providing the same JavaScript interface to Csound.
Installation
On Windows, simply download the current Csound installer from SourceForge and use it to install Csound on your computer. HTML is enabled by default in CsoundQt, which is included in the installer.
On Android, simply download the current Csound6.apk from SourceForge and use it to install Csound on your Android device. This can be any reasonably powerful Android smartphone or tablet. HTML is enabled by default, but the HTML5 features that are available will depend upon your version of Android.
Currently, WebGL may or may not be enabled on Android, depending on your versions of hardware and software.
Tutorial User Guide
Let's get started and do a few things in the simplest possible way, in a series of "toots." These pieces also are included in the examples/html directory of the Windows installation and can be found in the Csound Git repository as well.
- Display "Hello, World, this is Csound!" in HTML.
- Create a button that will generate a series of notes based on the logistic equation.
- Create a slider to set the value of the parameter that controls the degree of chaos produced by iterating the logistic equation, and two other sliders to control the frequency ratio and modulation index of the FM instrument that plays the notes from the logistic equation.
- Style the HTML elements using a style sheet.
01_HelloWorld.csd
This is the bare minimum CSD that shows some HTML output. In its entirety it is:
<CsoundSynthesizer> <CsOptions> </CsOptions> <CsInstruments> sr = 44100 ksmps = 128 nchnls = 2 0dbfs = 1.0 </CsInstruments> <html> Hello, World, this is Csound! </html> <CsScore> </CsScore> </CsoundSynthesizer>
Not much to it. HTML is full of graceful defaults. In HTML, plain text without any tags is imply printed as plain text.
02_ScoreGenerator.csd
Here I have introduced a simple Csound orchestra consisting of a single frequency modulation instrument feeding first into a reverberation effect, and then into a master output unit. These are connected using the signal flow graph opcodes. The actual orchestra is of little interest here. And this piece has no score, because the score will be generated at run time. In the <html> element, I also have added this button:
<button onclick="generate()"> Generate score </button>
When this button is clicked, it calls a JavaScript function that uses the logistic equation, which is a simple quadratic dynamical system, to generate a Csound score from a chaotic attractor of the system. This function also is quite simple. Its main job, aside from iterating the logistic equation a few hundred times, is to translate each iteration of the system into a musical note and send that note to Csound to be played using the Csound API function readScore(). So the following <script> element is added to the body of the <html> element:
<script>
var c = 0.99;
var y = 0.5;
function generate() {
csound.message("generate()...\n");
for (i = 0; i < 200; i++) {
var t = i * (1.0 / 3.0);
var y1 = 4.0 * c * y * (1.0 - y);
y = y1;
var key = Math.round(36.0 + (y * 60.0));
var note = "i 1 " + t + " 2.0 " + key + " 60 0.0 0.5\n";
csound.readScore(note);
};
};
</script>
03_Sliders.csd
The next step is to add more user control to this piece. We will enable the user to control the attractor of the piece by varying the constant c, and we will enable the user to control the sound of the Csound orchestra by varying the frequency modulation index, frequency modulation carrier ratio, reverberation time, and master output level.
This code is demonstrated on a low level, so that you can see all of the details and understand exactly what is going on. A real piece would most likely be written at a higher level of abstraction, for example by using a third party widget toolkit, such as jQuery UI.
A slider in HTML is just an 'input' element like this:
<input type=range min=0 max=1 value=.5 id=sliderC step=0.001 oninput="on_sliderC(value)">
This element has attributes of minimum value 0, maximum value 1, which normalizes the user's possible values between 0 and 1. This could be anything, but in many musical contexts, for example VST plugins, user control values are always normalized between 0 and 1. The tiny 'step' attribute simply approximates a continuous range of values.
The most important thing is the 'oninput' attribute, which sets the value of a JavaScript event handler for the 'oninput' event. This function is called whenever the user changes the value of the slider.
For ease of understanding, a naming convention is used here, with 'sliderC' being the basic name and other names of objects associated with this slider taking names built up by adding prefixes or suffixes to this basic name.
Normally a slider has a label, and it is convenient to show the actual numerical value of the slider. This can be done like so:
<table> <col width="2*"> <col width="5*"> <col width="100px"> <tr> <td> <label for=sliderC>c</label> <td> <input type=range min=0 max=1 value=.5 id=sliderC step=0.001 oninput="on_sliderC(value)"> <td> <output for=sliderC id=sliderCOutput>.5</output> </tr> </table>
If the slider, its label, and its numeric display are put into an HTML table, that table will act like a layout manager in a standard widget toolkit, and will resize the contained elements as required to get them to line up.
For this slider, the JavaScript handler is:
function on_sliderC(value) {
c = parseFloat(value);
document.querySelector('#sliderCOutput').value = c;
}
The variable c was declared at global scope just above the generate() function, so that variable is accessible within the on_sliderC function.
Keep in mind, if you are playing with this code, that a new value of c will only be heard when a new score is generated.
Very similar logic can be used to control variables in the Csound orchestra. The value of the slider has to be sent to Csound using the channel API, like this:
function on_sliderFmIndex(value) {
var numberValue = parseFloat(value);
document.querySelector('#sliderFmIndexOutput').value = numberValue;
csound.setControlChannel('gk_FmIndex', numberValue);
}
Then, in the Csound orchestra, that value has to be retrieved using the chnget opcode and applied to the instrument to which it pertains. It is most efficient if the variables controlled by channels are global variables declared just above their respective instrument definitions. The normalized values can be rescaled as required in the Csound instrument code.
gk_FmIndex init 0.5
instr ModerateFM
...
kindex = gk_FmIndex * 20
...
endin
Also for the sake of efficiency, a global, always-on instrument can be used to read the control channels and assign their values to these global variables:
instr Controls gk_FmIndex_ chnget "gk_FmIndex" if gk_FmIndex_ != 0 then gk_FmIndex = gk_FmIndex_ endif gk_FmCarrier_ chnget "gk_FmCarrier" if gk_FmCarrier_ != 0 then gk_FmCarrier = gk_FmCarrier_ endif gk_ReverberationDelay_ chnget "gk_ReverberationDelay" if gk_ReverberationDelay_ != 0 then gk_ReverberationDelay = gk_ReverberationDelay_ endif gk_MasterLevel_ chnget "gk_MasterLevel" if gk_MasterLevel_ != 0 then gk_MasterLevel = gk_MasterLevel_ endif endin
Note that each actual global variable has a default value, which is only overridden if the user actually operates its slider.
04_CustomStyle.csd
The default appearance of HTML elements is brutally simple. But each element has attributes that can be used to change its appearance, and these offer a great deal of control.
Of course, setting for example the font attribute for each label on a complex HTML layout is tedious. Therefore, this example shows how to use a style sheet. We don't need much style to get a much improved appearance:
<style type="text/css">
input[type='range'] {
-webkit-appearance: none;
border-radius: 5px;
box-shadow: inset 0 0 5px #333;
background-color: #999;
height: 10px;
width: 100%;
vertical-align: middle;
}
input[type=range]::-webkit-slider-thumb {
-webkit-appearance: none;
border: none;
height: 16px;
width: 16px;
border-radius: 50%;
background: yellow;
margin-top: -4px;
border-radius: 10px;
}
table td {
border-width: 2px;
padding: 8px;
border-style: solid;
border-color: transparent;
color:yellow;
background-color: teal;
font-family: sans-serif
}
</style>
This little style sheet is generic, that is, it applies to every element on the HTML page. It says, for example, that 'table td' (table cells) are to have a yellow sans-serif font on a teal background, and this will apply to every table cell on the page. Style sheets can be made more specialized by giving them names. But for this kind of application, that is not usually necessary.
Conclusion
Most, if not all all, of the functions performed by other Csound front ends could be encompassed by HTML and JavaScript. However, there are a few gotchas. For CsoundQt and other front ends based on Chrome, there may be extra latency and processing overhead required by inter-process communications. For Emscripten and other applications that use Web Audio, there may also be additional latency.
Obviously, much more can be done with HTML, JavaScript, and other Web standards found in contemporary Web browsers. Full-fledged, three-dimensional, interactive, multi-player computer games are now being written with HTML and JavaScript. Other sorts of Web applications also are being written this way.
Sometimes, JavaScript is embedded into an application for use as a scripting language. The Csound front ends discussed here are examples, but there are others. For example, Max for Live can be programmed in JavaScript, and so can the open source score editor MuseScore. In fact, in MuseScore, JavaScript can be used to algorithmically generate notated scores.
13 EXTENDING CSOUND
EXTENDING CSOUND
Developing Plugin Opcodes
Csound is possibly one of the most easily extensible of all modern music programming languages. The addition of unit generators (opcodes) and function tables is generally the most common type of extension to the language. This is possible through two basic mechanisms: user-defined opcodes (UDOs), written in the Csound language itself and pre-compiled/binary opcodes, written in C or C++.
To facilitate the latter case, Csound offers a simple opcode development API, from which dynamically-loadable, or ‘plugin’ unit generators can be built. A similar mechanism for function tables is also available. For this we can use either the C++ or the C languages. C++ opcodes are written as classes derived from a template (‘pseudo-virtual’) base class OpcodeBase. In the case of C opcodes, we normally supply a module according to a basic description. The sections on plugin opcodes will use the C language. For those interested in object-oriented programming, alternative
C++ class implementations for the examples discussed in this text can be extrapolated from the original C code.
You may find additional information and examples at https://github.com/csound/opcode_sdk.
Csound data types and signals
The Csound language provides four basic data types: i-, k-, a- and f-types (there is also a fifth type, w, which will not be discussed here). These are used to pass the data between opcodes, each opcode input or output parameter relating to one of these types. The Csound i-type variable is used for initialisation variables, which will assume only one value in performance. Once set, they will remain constant throughout the instrument or UDO code, unless there is a reinitialisation pass. In a plugin opcode, parameters that receive i-type variables are set inside the initialisation part of the code, because they will not change during processing.
The other types are used to hold scalar (k-type) , vectorial (a-type) and spectral-frame (f) signal variables. These will change in performance, so parameters assigned to these variables are set and modified in the opcode processing function. Scalars will hold a single value, whereas vectors hold an array of values (a vector). These values are floating-point numbers, either 32- or 64-bit, depending on the executable version used, defined in C/C++ as a custom MYFLT type.
Plugin opcodes will use pointers to input and output parameters to read and write their input/output. The Csound engine will take care of allocating the memory used for its variables, so the opcodes only need to manipulate the pointers to the addresses of these variables.
A Csound instrument code can use any of these variables, but opcodes will have to accept specific types as input and will generate data in one of those types. Certain opcodes, known as polymorphic opcodes, will be able to cope with more than one type for a specific parameter (input or output). This generally implies that more than one version of the opcode will have to be implemented, which will be called depending on the parameter types used.
Plugin opcodes
Originally, Csound opcodes could only be added to the system as statically-linked code. This required that the user recompiled the whole Csound code with the added C module. The introduction of a dynamic-loading mechanism has provided a simpler way for opcode addition, which only requires the C code to be compiled and built as a shared, dynamic library. These are known in Csound parlance as plugin opcodes and the following sections are dedicated to their development process.
Anatomy of an opcode
The C code for a Csound opcode has three main programming components: a data structure to hold the internal data, an initialising function and a processing function. From an object-oriented perspective, an opcode is a simple class, with its attributes, constructor and perform methods. The data structure will hold the attributes of the class: input/output parameters and internal variables (such as delays, coefficients, counters, indices etc.), which make up its dataspace.
The constructor method is the initialising function, which sets some attributes to certain values, allocates memory (if necessary) and anything that is needed for an opcode to be ready for use. This method is called by the Csound engine when an instrument with its opcodes is allocated in memory, just before performance, or when a reinitialisation is required.
Performance is implemented by the processing function, or perform method, which is called when new output is to be generated. This happens at every control period, or ksmps samples. This implies that signals are generated at two different rates: the control rate, kr, and the audio rate, sr, which is kr * ksmps samples/sec. What is actually generated by the opcode, and how its perform method is implemented, will depend on its input and output Csound language data types.
Opcoding basics
C-language opcodes normally obey a few basic rules and their development require very little in terms of knowledge of the actual processes involved in Csound. Plugin opcodes will have to provide the three main programming components outlined above: a data structure plus the initialisation and processing functions. Once these elements are supplied, all we need to do is to add a line telling Csound what type of opcode it is, whether it is an i-, k- or a-rate based unit generator and what arguments it takes.
The data structure will be organised in the following fashion:
1. The OPDS data structure, holding the common components of all opcodes.
2. The output pointers (one MYFLT pointer for each output)
3. The input pointers (as above)
4. Any other internal dataspace member.
The Csound opcode API is defined by csdl.h, which should be included at the top of the source file. The example below shows a simple data structure for an opcode with one output and three inputs, plus a couple of private internal variables:
#include "csdl.h"
typedef struct _newopc {
OPDS h;
MYFLT *out;/* output pointer */
MYFLT *in1,*in2,*in3; /* input pointers */
MYFLT var1; /* internal variables */
MYFLT var2;
} newopc;
Initialisation
The initialisation function is only there to initialise any data, such as the internal variables, or allocate memory, if needed. The plugin opcode model in Csound 6 expects both the initialisation function and the perform function to return an int value, either OK or NOTOK. Both methods take two arguments: pointers to the CSOUND data structure and the opcode dataspace. The following example shows an example initialisation function. It initialises one of the variables to 0 and the other to the third opcode input parameter.
int newopc_init(CSOUND *csound, newopc *p){
p->var1 = (MYFLT) 0;
p->var2 = *p->in3;
return OK;
}
Control-rate performance
The processing function implementation will depend on the type of opcode that is being created. For control rate opcodes, with k- or i-type input parameters, we will be generating one output value at a time. The example below shows an example of this type of processing function. This simple example just keeps ramping up or down depending on the value of the second input. The output is offset by the first input and the ramping is reset if it reaches the value of var2 (which is set to the third input argument in the constructor above).
int newopc_process_control(CSOUND *csound, newopc *p){
MYFLT cnt = p->var1 + *(p->in2);
if(cnt > p->var2) cnt = (MYFLT) 0; /* check bounds */
*(p->out) = *(p->in1) + cnt; /* generate output */
p->var1 = cnt; /* keep the value of cnt */
return OK;
}
Audio-rate performance
For audio rate opcodes, because it will be generating audio signal vectors, it will require an internal loop to process the vector samples. This is not necessary with k-rate opcodes, because, as we are dealing with scalar inputs and outputs, the function has to process only one sample at a time. If we were to make an audio version of the control opcode above (disregarding its usefulness), we would have to change the code slightly. The basic difference is that we have an audio rate output instead of control rate. In this case, our output is a whole vector (a MYFLT array) with ksmps samples, so we have to write a loop to fill it. It is important to point out that the control rate and audio rate processing functions will produce exactly the same result. The difference here is that in the audio case, we will produce ksmps samples, instead of just one sample. However, all the vector samples will have the same value (which actually makes the audio rate function redundant, but we will use it just to illustrate our point).
Another important thing to consider is to support the --sample-accurate mode introduced in Csound 6. For this we will need to add code to start processing at an offset (when this is given), and finish early (if that is required). The opcode will then lookup these two variables (called "offset" and "early") that are passed to it from the container instrument, and act to ensure these are taken into account. Without this, the opcode would still work, but not support the sample-accurate mode.
int newopc_process_audio(CSOUND *csound, newopc *p){
int i, n = CS_KSMPS;
MYFLT *aout = p->out; /* output signal */
MYFLT cnt = p->var1 + *(p->in2);
uint32_t offset = p->h.insdshead->ksmps_offset;
uint32_t early = p->h.insdshead->ksmps_no_end;
/* sample-accurate mode mechanism */
if(offset) memset(aout, '\0', offset*sizeof(MYFLT));
if(early) {
n -= early;
memset(&aout[n], '\0', early*sizeof(MYFLT));
}
if(cnt > p->var2) cnt = (MYFLT) 0; /* check bounds */
/* processing loop */
for(i=offset; i < n; i++) aout[i] = *(p->in1) + cnt;
p->var1 = cnt; /* keep the value of cnt */
return OK;
}
In order for Csound to be aware of the new opcode, we will have to register it. This is done by filling an opcode registration structure OENTRY array called localops (which is static, meaning that only one such array exists in memory at a time):
static OENTRY localops[] = {
{ "newopc", sizeof(newopc), 0, 7, "s", "kki",(SUBR) newopc_init,
(SUBR) newopc_process_control, (SUBR) newopc_process_audio }
};
LINKAGE
The OENTRY structure defines the details of the new opcode:
- the opcode name (a string without any spaces).
- the size of the opcode dataspace, set using the macro S(struct_name), in most cases; otherwise this is a code indicating that the opcode will have more than one implementation, depending on the type of input arguments (a polymorphic opcode).
- Flags to control multicore operation (0 for most cases).
- An int code defining when the opcode is active: 1 is for i-time, 2 is for k-rate and 4 is for a-rate. The actual value is a combination of one or more of those. The value of 7 means active at i-time (1), k-rate (2) and a-rate (4). This means that the opcode has an init function, plus a k-rate and an a-rate processing functions.
- String definition the output type(s): a, k, s (either a or k), i, m (multiple output arguments), w or f (spectral signals).
- Same as above, for input types: a, k, s, i, w, f, o (optional i-rate, default to 0), p (opt, default to 1), q (opt, 10), v(opt, 0.5), j(opt, ?1), h(opt, 127), y (multiple inputs, a-type), z (multiple inputs, k-type), Z (multiple inputs, alternating k- and a-types), m (multiple inputs, i-type), M (multiple inputs, any type) and n (multiple inputs, odd number of inputs, i-type).
- I-time function (init), cast to (SUBR).
- K-rate function.
- A-rate function.
Since we have defined our output as 's', the actual processing function called by csound will depend on the output type. For instance
k1 newopc kin1, kin2, i1
will use newopc_process_control(), whereas
a1 newopc kin1, kin2, i1
will use newopc_process_audio(). This type of code is found for instance in the oscillator opcodes, which can generate control or audio rate (but in that case, they actually produce a different output for each type of signal, unlike our example).
Finally, it is necessary to add, at the end of the opcode C code the LINKAGE macro, which defines some functions needed for the dynamic loading of the opcode.
Building opcodes
The plugin opcode is build as a dynamic module. All we need is to build the opcode as a dynamic library, as demonstrated by the examples below.
On OSX:
gcc -O2 -dynamiclib -o myopc.dylib opsrc.c -DUSE_DOUBLE -I/Library/Frameworks/CsoundLib64.framework/Headers
Linux:
gcc -O2 -shared -o myopc.so -fPIC opsrc.c -DUSE_DOUBLE -I<path to Csound headers>
Windows (MinGW+MSYS):
gcc -O2 -shared -o myopc.dll opsrc.c -DUSE_DOUBLE -I<path to Csound headers>
CSD Example
To run Csound with the new opcodes, we can use the --opcode-lib=libname option.
<CsoundSynthesizer> <CsOptions> --opcode-lib=newopc.so ; OSX: newopc.dylib; Windows: newopc.dll </CsOptions> <CsInstruments> schedule 1,0,100,440 instr 1 asig newopc 0, 0.001, 1 ksig newopc 1, 0.001, 1.5 aosc oscili 1000, p4*ksig outs aosc*asig endin </CsInstruments> </CsoundSynthesizer> ;example by victor lazzarini
OPCODE GUIDE
OPCODE GUIDE: OVERVIEW
If you run Csound from the command line with the option -z, you get a list of all opcodes. Currently (Csound 5.13), the total number of all opcodes is about 1500. There are already overviews of all of Csound's opcodes in the Opcodes Overview and the Opcode Quick Reference of the Canonical Csound Manual.
This chapter is another attempt to provide some orientation within Csound's wealth of opcodes. Unlike the references mentioned above, not all opcodes are listed here, but the ones that are, are commented upon briefly. Some opcodes appear more than once and in different sections to reflect the different contexts in which they could be used. This guide intends to provide insights into the opcodes listed that the other sources do not.
BASIC SIGNAL PROCESSING
-
OSCILLATORS AND PHASORS
-
ENVELOPES
-
DELAYS
-
FILTERS
Compare Standard Filters and Specialized Filters overviews.
-
SIGNAL MEASUREMENT, DYNAMIC PROCESSING, SAMPLE LEVEL OPERATIONS
-
SPATIALIZATION
ADVANCED SIGNAL PROCESSING
-
MODULATION AND DISTORTION
-
FFT AND SPECTRAL PROCESSING
-
PHYSICAL MODELS AND FM INSTRUMENTS
DATA
-
BUFFER / FUNCTION TABLES
-
SIGNAL INPUT/OUTPUT, SAMPLE AND LOOP PLAYBACK, SOUNDFONTS
-
Signal Input and Output
-
Sample Playback With Optional Looping
flooper2 sndloop -
Soundfonts and Fluid Opcodes
fluidEngine fluidSetInterpMethod fluidLoad fluidProgramSelect fluidNote fluidCCi fluidCCk fluidControl fluidOut fluidAllOut
-
-
FILE INPUT AND OUTPUT
-
PRINTING AND STRINGS
REALTIME INTERACTION
-
MIDI
-
OPEN SOUND CONTROL AND NETWORK
-
Open Sound Control
-
Remote Instruments
-
Network Audio
-
-
HUMAN INTERFACES
-
Widgets
FLTK overview here
-
Keys
-
Mouse
-
WII
-
P5 Glove
-
INSTRUMENT CONTROL
-
SCORE PARAMETER ACCESS
-
TIME AND TEMPO
-
EVENT TRIGGERING
event_i / event scoreline_i / scoreline schedkwhen seqtime /seqtime2 timedseq
-
INSTRUMENT SUPERVISION
MATHS
-
MATHEMATICAL CALCULATIONS
-
CONVERTERS
PYTHON AND SYSTEM
PLUGINS
-
PLUGIN HOSTING
-
EXPORTING CSOUND FILES TO PLUGINS
OPCODE GUIDE: BASIC SIGNAL PROCESSING
-
OSCILLATORS AND PHASORS
-
Standard Oscillators
oscils is a very simple sine oscillator which is ideally suited for quick tests. It needs no function table, but offers just i-rate input arguments.
ftgen generates a function table, which is needed by any oscillator except oscils. The GEN Routines fill the function table with any desired waveform, either a sine wave or any other curve. Refer to the function table chapter of this manual for more information.
poscil can be recommended as standard oscillator because it is very precise, in particular for long tables and low frequencies. It provides linear interpolation, any rate its amplitude and frequency input arguments, and works also for non-power-of-two tables. poscil3 provides cubic interpolation, but has just k-rate input. Other common oscillators are oscili and oscil3. They are less precise than poscil/poscili, but you can skip the initialization which can be useful in certain situations. The oscil opcode does not provide any interpolation, so it should usually be avoided. More Csound oscillators can be found here.
-
Dynamic Spectrum Oscillators
buzz and gbuzz generate a set of harmonically related cosine partials.
mpulse generates a set of impulses of user-definable amplitude and interval gap between impulses.
vco and vco2 implement band-limited, analogue modelled oscillators that can use variety of standard waveforms.
-
Phasors
phasor produces the typical moving phase values between 0 and 1. The more complex syncphasor lets you synchronize more than one phasor precisely.
-
-
RANDOM AND NOISE GENERATORS
seed sets the seed value for the majority of the Csound (pseudo) random number generators. A seed value of zero will seed random number generators from the system clock thereby guaranteeing a different result each time Csound is run, while any other seed value generates the same random values each time.
rand is the usual opcode for uniformly distributed bipolar random values. If you give 1 as input argument (called "amp"), you will get values between -1 and +1. randi interpolates between values which are generated with a variable frequency. randh holds the value until the next one is generated (sample and hold). You can control the seed value by an input argument (a value greater than 1 seeds from current time), you can decide whether to generate 16bit or 31bit random numbers and you can add an offset.
rnd31 can output all rates of variables (i-rate variables are not supported by rand). It also gives the user control over the random distribution, but has no offset parameter.
random provides extra conveniece in that the user can define both the minimum and a maximum of the distribution as input argument; rand and rnd31 only output bipolar ranges and we define amplitude. It can also be used for all rates, but you have no direct seed input, and the randomi/randomh variants always start from the lower border, instead anywhere between the borders.
pinkish produces pink noise at audio-rate (white noise can be produced using rand or noise).
There are many more random opcodes worth investigating. Here is an overview. A number of GEN routines are also used for generating random distributions. They can be found in the GEN Routines overview.
-
ENVELOPES
-
Simple Standard Envelopes
linen applies a linear rise (fade in) and decay (fade out) to a signal. It is very easy to use, as you put the raw audio signal in and get the enveloped signal out.
linenr does the same for any note whose duration is not known when they begin. This could mean MIDI notes or events triggered in real time. linenr begins the final stage of the envelope only when that event is turned off (released). The penultimate value is held until this release is received.
adsr calculates the classic attack-decay-sustain-release envelope. The result is to be multiplied with the audio signal to get the enveloped signal.
madsr does the same for notes triggered in real time (functioning in a similar way to linenr explained above).
Other standard envelope generators can be found in the Envelope Generators overview of the Canonical Csound Manual.
-
Envelopes By Linear And Exponential Generators
linseg creates one or more segments of lines between specified points.
expseg does the same but with exponential segments. Note that zero values or crossing the zero axis are illegal.
transeg is particularly flexible as you can specify the shape of each segment individually (continuously from convex to linear to concave).
All of these opcodes have 'r' variants (linsegr, expsegr, transegr) for MIDI or other real time triggered events. ('r' stands for 'release'.)
More opcodes for generating envelopes can be found in this overview.
-
Envelopes By Function Tables
Any function table (or part of it) can be used as envelope. Once a function table has been created using ftgen or a GEN Routine it can then be read using an oscillator, and multiply the result with the audio signal you want to envelope.
-
-
DELAYS
-
Audio Delays
The vdelay family of opcodes are easy to use and implement all the necessary features expected when working with delays:
vdelay implements a variable delay at audio rate with linear interpolation.
vdelay3 offers cubic interpolation.
vdelayx has an even higher quality interpolation (and is for this reason slower). vdelayxs lets you input and output two channels, and vdelayxq four.
vdelayw changes the position of the write tap in the delay line instead of the read tap. vdelayws is for stereo, and vdelaywq for quadro.
The delayr/delayw opcodes establishes a delay line in a more complicated way. The advantage is that you can have as many taps in one delay line as you need.
delayr establishes a delay line and reads from the end of it.
delayw writes an audio signal to the delay line.
deltap, deltapi, deltap3, deltapx and deltapxw function in a similar manner to the relevant opcodes of the vdelay family (see above) bearing the same suffixes.
deltapn offers a tap delay measured in samples, not seconds. This might be more useful in the design of filters -
Control Delays
delk and vdel_k let you delay any k-signal by some time interval (useful, for instance, as a kind of 'wait' function).
-
-
FILTERS
Csound boasts an extensive range of filters and they can all be perused on the Csound Manual pages for Standard Filters and Specialized Filters. Here, some of the most frequently used filters are mentioned, and some tips are given. Note that filters usually change the signal level, so you may also find the balance opcode useful.
-
Low Pass Filters
tone is a first order recursive low pass filter. tonex implements a series of tone filters.
butlp is a second order low pass Butterworth filter.
clfilt lets you choose between different filter types and different numbers of poles in the design.
-
High Pass Filters
atone is a first order recursive high pass filter. atonex implements a series of atone filters.
buthp is a second order high pass Butterworth filter.
clfilt lets you choose between different filter types and different numbers of poles in the design.
-
Band Pass And Resonant Filters
reson is a second order resonant filter. resonx implements a series of reson filters, while resony emulates a bank of second order bandpass filters in parallel. resonr and resonz are variants of reson with variable frequency response.
butbp is a second order band-pass Butterworth filter.
-
-
REVERB
Note that you can easily work in Csound with convolution reverbs based on impulse response files, for instance with pconvolve.
freeverb is the implementation of Jezar's well-known free (stereo) reverb.
reverbsc is a stereo FDN reverb, based on work of Sean Costello.
reverb and nreverb are the traditional Csound reverb units.
babo is a physical model reverberator ("ball within the box").
-
SIGNAL MEASUREMENT, DYNAMIC PROCESSING, SAMPLE LEVEL OPERATIONS
-
Amplitude Measurement And Amplitude Envelope Following
rms determines the root-mean-square amplitude of an audio signal.
balance adjusts the amplitudes of an audio signal according to the rms amplitudes of another audio signal.
follow / follow2 are envelope followers which report the average amplitude in a certain time span (follow) or according to an attack/decay rate (follow2).
peak reports the highest absolute amplitude value received.
max_k outputs the local maximum or minimum value of an incoming audio signal, checked in a certain time interval.
-
Pitch Estimation
ptrack, pitch and pitchamdf track the pitch of an incoming audio signal, using different methods.
pvscent calculates the spectral centroid for FFT streaming signals (see below under "FFT And Spectral Processing")
-
Tempo Estimation
tempest estimates the tempo of beat patterns in a control signal.
-
Dynamic Processing
compress compresses, limits, expands, ducks or gates an audio signal.
dam is a dynamic compressor/expander.
clip clips an a-rate signal to a predefined limit, in a “soft” manner. -
Sample Level Operations
limit sets the lower and upper limits of an incoming value (all rates).
samphold performs a sample-and-hold operation on its a- or k-input.
vaget / vaset allow getting and setting certain samples of an audio vector at k-rate.
-
-
SPATIALIZATION
-
Panning
pan2 distributes a mono audio signal across two channels according to a variety of panning laws.
pan distributes a mono audio signal amongst four channels.
-
VBAP
vbaplsinit configures VBAP output according to loudspeaker parameters for a 2- or 3-dimensional space.
vbap4 / vbap8 / vbap16 distributes an audio signal among up to 16 channels, with k-rate control over azimut, elevation and spread. -
Ambisonics
bformenc1 encodes an audio signal to the Ambisonics B format.
bformdec1 decodes Ambisonics B format signals to loudspeaker signals in different possible configurations. -
Binaural / HRTF
hrtfstat, hrtfmove and hrtfmove2 are opcodes for creating 3d binaural audio for headphones. hrtfer is an older implementation. All of these opcodes require data files containing information about the sound shadowing qualities of the human head and ears.
-
OPCODE GUIDE: ADVANCED SIGNAL PROCESSING
-
MODULATION AND DISTORTION
-
Frequency Modulation
foscil and foscili implement composite units for FM in the Chowning setup.
crossfm, crossfmi, crosspm, crosspmi, crossfmpm and crossfmpmi are different units for cross-frequency and cross-phase modulation.
-
Distortion And Wave Shaping
distort and distort1 perform waveshaping using a function table (distort) or by modified hyperbolic tangent distortion (distort1).
powershape waveshapes a signal by raising it to a variable exponent.
polynomial efficiently evaluates a polynomial of arbitrary order.
chebyshevpoly efficiently evaluates the sum of Chebyshev polynomials of arbitrary order.
GEN03, GEN13, GEN14 and GEN15 are also used for waveshaping. -
Flanging, Phasing, Phase Shaping
flanger implements a user controllable flanger.
harmon analyzes an audio input and generates harmonizing voices in synchrony.
phaser1 and phaser2 implement first- or second-order allpass filters arranged in a series.
pdclip, pdhalf and pdhalfy are useful for phase distortion synthesis. -
Doppler Shift
doppler lets you calculate the doppler shift depending on the position of the sound source and the microphone.
-
-
GRANULAR SYNTHESIS
partikkel is the most flexible opcode for granular synthesis. You should be able to do everything you like in this field. The only drawback is the large number of input arguments, so you may want to use other opcodes for certain purposes.
You can find a list of other relevant opcodes here.
sndwarp focusses granular synthesis on time stretching and/or pitch modifications. Compare waveset and the pvs-opcodes pvsfread, pvsdiskin, pvscale, pvshift for other implementations of time and/or pitch modifications.
-
CONVOLUTION
pconvolve performs convolution based on a uniformly partitioned overlap-save algorithm.
ftconv is similar to pconvolve, but you can also use parts of the impulse response file, instead of reading the whole file. It also permits the use of multichannel impulse files (up to 8-channels) to create multichannel outputs.
dconv performs direct convolution.
-
FFT AND SPECTRAL PROCESSING
-
Realtime Analysis And Resynthesis
pvsanal performs a Fast Fourier Transformation of an audio stream (a-signal) and stores the result in an f-variable.
pvstanal creates an f-signal directly from a sound file which is stored in a function table (usually via GEN01).
pvsynth performs an Inverse FFT (takes a f-signal and returns an audio-signal).
pvsadsyn is similar to pvsynth, but resynthesizes with a bank of oscillators, instead of direct IFFT.
-
Writing FFT Data To a File and Reading From it
pvsfwrite writes an f-signal (= the FFT data) from inside Csound to a file. This file has the PVOCEX format and uses the file extension .pvx.
pvanal actually does the same as Csound Utility (a seperate program which can be called in QuteCsound or via the Terminal). In this case, the input is an audio file.
pvsfread reads the FFT data from an existing .pvx file. This file can be generated by the Csound Utility pvanal. Reading of the file is carried out using a time pointer.
pvsdiskin is similar to pvsfread, but reading is done by a speed argument.
-
Writing FFT Data To a Buffer and Reading From it
pvsbuffer writes an f-signal into a circular buffer that it also creates.
pvsbufread reads an f-signal from a buffer which was created by pvsbuffer.
pvsftw writes amplitude and/or frequency data from a f-signal to a function table.
pvsftr transforms amplitude and/or frequency data from a function table to a f-signal.
-
FFT Info
pvsinfo gets information, either from a realtime f-signal or from a .pvx file.
pvsbin gets the amplitude and frequency values from a single bin of an f-signal.
pvscent calculates the spectral centroid of a signal.
-
Manipulating FFT Signals
pvscale transposes the frequency components of a f-stream by simple multiplication.
pvshift changes the frequency components of a f-stream by adding a shift value, starting at a certain bin.
pvsbandp and pvsbandr applies a band pass and band reject filter to the frequency components of a f-signal.
pvsmix, pvscross, pvsfilter, pvsvoc and pvsmorph perform different methods of cross synthesis between two f-signals.
pvsfreeze freezes the amplitude and/or frequency of an f-signal according to a k-rate trigger.
pvsmaska, pvsblur, pvstencil, pvsarp, pvsmooth perform a variety of other manipulations on a stream of FFT data.
-
-
PHYSICAL MODELS AND FM INSTRUMENTS
OPCODE GUIDE: DATA
-
BUFFER / FUNCTION TABLES
See the chapter about function tables for more detailed information.
-
Creating Function Tables (Buffers)
ftgen can generates function tables from within the orchestra. The function table will exist until the end of the current Csound performance. Different GEN Routines are used to fill a function table with different kinds of data. This could be waveforms, sound files, envelopes, window functions and so on.
-
Writing To Tables
tableiw / tablew: Write values to a function table at i-rate (tableiw), k-rate and a-rate (tablew). These opcodes provide many options and are robust in use as they check for user error in defining table reading index values. They may however experience problems with non-power-of-two table sizes.tabw_i / tabw: Write values to a function table at i-rate (tabw_i), k-rate or a-rate (tabw). These opcodes offer fewer options than tableiw and tablew but will work consistently with non-power-of-two table sizes. They do not provide a boundary check on index values given to them which makes them fast but also then demands user responsibility in protecting against invalid index values.
-
Reading From Tables
table / tablei / table3: Read values from a function table at any rate, either by direct indexing (table), or by linear interpolation (tablei) or cubic interpolation (table3). These opcodes provide many options and are robust in use as they check for user error in defining table reading index values. They may however experience problems with non-power-of-two table sizes.
tab_i / tab: Read values from a function table at i-rate (tab_i), k-rate or a-rate (tab). They offer no interpolation and fewer options than the table opcodes but they will also work with non-power-of-two table sizes. They do not provide a boundary check which makes them fast but also give the user the responsibility not to read any value beyond the table boundaries.
-
Saving Tables to Files
ftsave / ftsavek: Save a function table as a file, at i-time (ftsave) or at k-rate (ftsavek). These files can be text files or binary files but not sound files. To save a table as a sound file you can use the user defined opcode TableToSF.
-
Reading Tables From Files
ftload / ftloadk: Load a function table which has previously been saved using ftsave/ftsavek.
GEN23 transfers the contents of a text file into a function table.
-
-
SIGNAL INPUT/OUTPUT, SAMPLE AND LOOP PLAYBACK, SOUNDFONTS
-
Signal Input And Output
inch read the audio input from any channel of your audio device. Make sure you have the nchnls value in the orchestra header set properly.
outch writes any audio signal(s) to any output channel(s). If Csound is in realtime mode (by the flag '-o dac' or by the 'Render in Realtime' mode of a frontend like QuteCsound), the output channels are the channels of your output device. If Csound is in 'Render to file' mode (by the flag '-o mysoundfile.wav' or the the frontend's choice), the output channels are the channels of the soundfile which is being written. Make sure you have the nchnls value in the orchestra header set properly to get the number of channels you wish to have.
out and outs are frequently used for mono and stereo output. They always write to channel 1 (out) or channels 1 and 2 (outs).
monitor can be used (in an instrument with the highest number) to gather the sum of all audio on all output channels.
-
Sample Playback With Optional Looping
flooper2 is a function table based crossfading looper.
sndloop records input audio and plays it back in a loop with user-defined duration and crossfade time.
Note that there are additional user defined opcodes for the playback of samples stored in buffers / function tables.
-
Soundfonts And Fluid Opcodes
fluidEngine instantiates a FluidSynth engine.
fluidSetInterpMethod sets an interpolation method for a channel in a FluidSynth engine.
fluidLoad loads SoundFonts.
fluidProgramSelect assigns presets from a SoundFont to a FluidSynth engine's MIDI channel.
fluidNote plays a note on a FluidSynth engine's MIDI channel.
fluidCCi sends a controller message at i-time to a FluidSynth engine's MIDI channel.
fluidCCk sends a controller message at k-rate to a FluidSynth engine's MIDI channel.
fluidControl plays and controls loaded Soundfonts (using 'raw' MIDI messages).
fluidOut receives audio from a single FluidSynth engine.
fluidAllOut receives audio from all FluidSynth engines.
-
-
FILE INPUT AND OUTPUT
-
Sound File Input
soundin reads from a sound file (up to 24 channels). It is important to ensure that the sr value in the orchestra header matches the sample rate of your sound file otherwise the sound file will play back at a different speed and pitch.
diskin is like soundin, but can also alter the speed of reading also resulting in higher or lower pitches. There is also the option to loop the file.
diskin2 is similar to diskin, but it automatically converts the sample rate of the sound file if it does not match the sample rate of the orchestra. It also offers different interpolation methods to implement different levels of sound quality when sound files are read at altered speeds.
GEN01 loads a sound file into a function table (buffer).
mp3in facilitates the playing of mp3 sound files. -
Sound File Queries
filelen returns the length of a sound file in seconds.
filesr returns the sample rate of a sound file.
filenchnls returns the number of channels of a sound file.
filepeak returns the peak absolute value of a sound file, either of one specified channel, or from all channels. Make sure you have set 0dbfs to 1; otherwise you will get values relative to Csound's default 0dbfs value of 32768.
filebit returns the bit depth of a sound file. -
Sound File Output
Keep in mind that Csound always writes output to a file if you have set the '-o' flag to the name of a sound file (or if you choose 'render to file' in a front-end like QuteCound).
fout writes any audio signal(s) to a file, regardless of whether Csound is in realtime or non-realtime mode. This opcode is recommended for rendering a realtime performance as a sound file on disc.
-
Non-Soundfile Input And Output
readk can read data from external files (for instance a text file) and transform them to k-rate values.
GEN23 transfers a text file into a function table.
dumpk writes k-rate signals to a text file.
fprints / fprintks write any formatted string to a file. If you call this opcode several times during one performance, the strings are appended. If you write to an pre-existing file, the file will be overwritten.
ftsave / ftsavek: Save a function table as a binary or text file, in a specific format.
ftload / ftloadk: Load a function table which has been written by ftsave/ftsavek.
-
-
CONVERTERS OF DATA TYPES
-
i <- k
i(k) returns the value of a k-variable at init-time. This can be useful to get the value of GUI controllers, or when using the reinit feature.
-
k <- a
downsamp converts an a-rate signal to a k-rate signal, with optional averaging.
max_k returns the maximum of an k-rate signal in a certain time span, with different options of calculation -
a <- k
upsamp converts a k-rate signal to an a-rate signal by simple repetitions. It is the same as the statement asig=ksig.
interp converts a k-rate signal to an a-rate signal by interpolation.
-
-
PRINTING AND STRINGS
-
Simple Printing
print is a simple opcode for printing i-variables. Note that the printed numbers are rounded to 3 decimal places.
printk is its counterpart for k-variables. The itime argument specifies the time in seconds between printings (itime=0 means one printout in each k-cycle which is usually some thousand printings per second).
printk2 prints a k-variable whenever it changes.
puts prints S-variables. The ktrig argument lets you print either at i-time or at k-rate. -
Formatted Printing
prints lets you print a format string at i-time. The format is similar to the C-style syntax but there is no %s format, therefore string variables cannot can be printed.
printf_i is very similar to prints. It also works at init-time. The advantage in comparision to prints is the ability of printing string variables. On the other hand, you need a trigger and at least one input argument.
printks is like prints, but takes k-variables, and like printk, you must specify a time between printing.
printf is like printf_i, but works at k-rate. -
String Variables
sprintf works like printf_i, but stores the output in a string variable, instead of printing it out.
sprintfk is the same for k-rate arguments.
strset links any string with a numeric value.
strget transforms a strset number back to a string. -
String Manipulation And Conversion
There are many opcodes for analysing, manipulating and converting strings. There is a good overview in the Canonical Csound Manual on this and that page.
-
OPCODE GUIDE: REALTIME INTERACTION
-
MIDI
-
Opcodes For Use In MIDI-Triggered Instruments
massign assigns specified midi channels to instrument numbers. See the Triggering Instrument Instances chapter for more information.
pgmassign assigns midi program changes to specified instrument numbers.
notnum retrieves the midi number of the key which has been pressed and activated this instrument instance.
cpsmidi converts this note number to the frequency in cycles per second (Hertz).
veloc and ampmidi get the velocity of the key which has been pressed and activated this instrument instance.
midichn returns the midi channel number from which the note was activated.
pchbend reads pitch bend information.
aftouch and polyaft read the monophonic aftertouch (afttouch) and polyphonic aftertouch (polyaft) information. -
Opcodes For Use In All Instruments
ctrl7 reads the values of a usual (7 bit) controller and scales it. ctrl14 and ctrl21 can be used for high definition controllers.
initc7 or ctrlinit set the initial value of 7 bit controllers. Use initc14 and initc21 for high definition devices.
midiin reads all incoming midi events.
midiout writes any type of midi message to the midi out port.
-
-
OPEN SOUND CONTROL AND NETWORK
-
Open Sound Control
OSCinit initialises a port for later use of the OSClisten opcode.
OSClisten receives messages of the port which was initialised by OSCinit.
OSCsend sends messages to a port.
-
Remote Instruments
remoteport defines the port for use with the remote system.
insremot will send note events from a source machine to one destination.
insglobal will send note events from a source machine to many destinations.
midiremot will send midi events from a source machine to one destination.
midiglobal will broadcast the midi events to all the machines involved in the remote concert. -
Network Audio
socksend sends audio data to other processes using the low-level UDP or TCP protocols.
sockrecv receives audio data from other processes using the low-level UDP or TCP protocols.
-
-
HUMAN INTERFACES
-
Widgets
The FLTK Widgets are integrated in Csound. Information and examples can be found here.
QuteCsound implements a more modern and easy-to-use system for widgets. The communication between the widgets and Csound is done via invalue (or chnget) and outvalue (or chnset).
-
Keys
sensekey reads the input of the computer keyboard.
-
Mouse
xyin reads the current mouse position. This should be used if your frontend does not provide any other means of reading mouse information.
-
WII
wiiconnect reads data from a number of external Nintendo Wiimote controllers.
wiidata reads data fields from a number of external Nintendo Wiimote controllers.
wiirange sets scaling and range limits for certain Wiimote fields.
wiisend sends data to one of a number of external Wii controllers. -
P5 Glove
p5gconnect reads data from an external P5 glove controller.
p5gdata reads data fields from an external P5 glove controller.
-
OPCODE GUIDE: INSTRUMENT CONTROL
-
SCORE PARAMETER ACCESS
p(x) gets the value of a specified p-field. (So, 'p(5)' and 'p5' both return the value of the fifth parameter in a certain score line, but in the former case you can insert a variable to specify the p-field.
pindex does actually the same, but as an opcode instead of an expression.
pset sets p-field values in case there is no value from a scoreline.
passign assigns a range of p-fields to i-variables.
pcount returns the number of p-fields belonging to a note event. -
TIME AND TEMPO
-
Time Reading
times / timek return the time in seconds (times) or in control cycles (timek) since the start of the current Csound performance.
timeinsts / timeinstk return the time in seconds (timeinsts) or in control cycles (timeinstk) since the start of the instrument in which they are defined.
date / dates return the number of seconds since 1 January 1970, using the operating system's clock, either as a number (date) or as a string (dates).
setscorepos sets the playback position of the current score performance to a given position. -
Tempo Reading
tempo allows the performance speed of Csound scored events to be controlled from within an orchestra.
miditempo returns the current tempo at k-rate, of either the midi file (if available) or the score.
tempoval reads the current value of the tempo.
-
Duration Modifications
ihold forces a finite-duration note to become a 'held' note.
xtratim extend the duration of the current instrument instance by a specified time duration. -
Time Signal Generators
metro outputs a metronome-like control signal (1 value impulses separated by zeroes). Rate of impulses can be specified as impulses per second
mpulse generates an impulse for one sample of user definable amplitude, followed by a user-definable time gap.
-
-
CONDITIONS AND LOOPS
changed reports whether any of its k-rate variable inputs has changed.
trigger informs whether a k-rate signal crosses a certain threshold, either in an upward direction, in a downward direction or both.
if branches conditionally at initialisation or during performance time.
loop_lt, loop_le, loop_gt and loop_ge perform loops either at i-time or at k-rate.
-
PROGRAM FLOW
init initializes a k- or a-variable (assigns a value to a k- or a-variable which is valid at i-time).
igoto jumps to a label at i-time.
kgoto jumps to a label at k-rate.
timout jumps to a label for a given time. Can be used in conjunction with reinit to perform time loops (see the chapter about Control Structures for more information).
reinit / rigoto / rireturn forces a certain section of code to be reinitialised (i.e. i-rate variables will be refreshed).
-
EVENT TRIGGERING
event_i / event: Generate an instrument event at i-time (event_i) or at k-time (event). Easy to use, but you cannot send a string to the subinstrument.
scoreline_i / scoreline: Generate an instrument at i-time (scoreline_i) or at k-time (scoreline). Like event_i/event, but you can send to more than one instrument but unlike event_i/event you can send strings. On the other hand, you must usually pre-format your scoreline-string using sprintf.
schedkwhen triggers an instrument event at k-time if a certain condition is given.
seqtime / seqtime2 can be used to generate a trigger signal according to time values in a function table.
timedseq is an event-sequencer in which time can be controlled by a time-pointer. Sequence data is stored in a function table or text file.
-
INSTRUMENT SUPERVISION
-
Instances And Allocation
active returns the number of active instances of an instrument.
maxalloc limits the number of allocations (instances) of an instrument.
prealloc creates space for instruments but does not run them.
-
Turning On And Off
turnon activates an instrument for an indefinite time.
turnoff / turnoff2 enables an instrument to turn itself, or another instrument, off.
mute mutes/unmutes new instances of a given instrument.
remove removes the definition of an instrument as long as it is not in use.
exitnow causes Csound to exit as fast as possible and with no cleaning up. -
Named Instruments
nstrnum returns the number of a named instrument.
-
-
SIGNAL EXCHANGE AND MIXING
-
chn opcodes
chn_k, chn_a, and chn_S declare a control, audio, or string channel. Note that this can be done implicitly in most cases by chnset/chnget.
chnset writes a value (i, k, S or a) to a software channel (which is identified by a string as its name).
chnget gets the value of a named software channel.
chnmix writes audio data to an named audio channel, mixing to the previous output.
chnclear clears an audio channel of the named software bus to zero. -
zak
zakinit initialised zak space for the storage of zak variables.
zaw, zkw and ziw write to (or overwrite) a-rate, k-rate or i-rate zak variables respectively.
zawm, zkwm and ziwm mix (accumulate) a-rate, k-rate or i-rate zak variables respectively.
zar, zkr and zir read from a-rate, k-rate or i-rate zak variables respectively.
zacl and zkcl clears a range of a-rate or k-rate zak variables respectively.
-
OPCODE GUIDE: MATH, PYTHON/ SYSTEM, PLUGINS
MATHS
-
MATHEMATICAL CALCULATIONS
-
Arithmetic Operations
+, -, *, /, ^, % are the usual signs for addition, subtraction, multiplication, division, raising to a power and modulo. The precedence is like that used in common mathematics (* binds stronger than + etc.), but you can change this behaviour with parentheses: 2^(1/12) returns 2 raised by 1/12 (= the 12st root of 2), while 2^1/12 returns 2 raised by 1, and the result divided by 12.
exp(x), log(x), log10(x) and sqrt(x) return e raised to the xth power, the natural log of x, the base 10 log of x, and the square root of x.
abs(x) returns the absolute value of a number.
int(x) and frac(x) return the integer respective the fractional part of a number.
round(x), ceil(x), floor(x) round a number to the nearest, the next higher or the next lower integer. -
Trigonometric Functions
sin(x), cos(x), tan(x) perform a sine, cosine or tangent function.
sinh(x), cosh(x), tanh(x) perform a hyperbolic sine, cosine or tangent function.
sininv(x), cosinv(x), taninv(x) and taninv2(x) perform the arcsine, arccosine and arctangent functions. -
Logic Operators
&& and || are the symbols for a logical "and" and "or". Note that you can use here parentheses for defining the precedence, too, for instance: if (ival1 < 10 && ival2 > 5) || (ival1 > 20 && ival2 < 0) then ...
! is the symbol for logical "not". For example: if (kx != 2) then ... would serve a conditional branch if variable kx was not equal to '2'.
-
-
CONVERTERS
-
MIDI To Frequency
cpsmidi converts a MIDI note number from a triggered instrument to the frequency in Hertz.
cpsmidinn does the same for any input values (i- or k-rate).
Other opcodes convert to Csound's pitch- or octave-class system. They can be found here.
-
Frequency To MIDI
Csound has no own opcode for the conversion of a frequency to a midi note number, because this is a rather simple calculation. You can find a User Defined Opcode for rounding to the next possible midi note number or for the exact translation to a midi note number and a cent value as fractional part.
-
Cent Values To Frequency
cent converts a cent value to a multiplier. For instance, cent(1200) returns 2, cent(100) returns 1.059403. If you multiply this with the frequency you reference to, you get frequency of the note which corresponds to the cent interval.
-
Amplitude Converters
ampdb returns the amplitude equivalent of the dB value. ampdb(0) returns 1, ampdb(-6) returns 0.501187, and so on.
ampdbfs returns the amplitude equivalent of the dB value, according to what has been set as 0dbfs (1 is recommended, the default is 15bit = 32768). So ampdbfs(-6) returns 0.501187 for 0dbfs=1, but 16422.904297 for 0dbfs=32768.
dbamp returns the decibel equivalent of the amplitude value, where an amplitude of 1 is the maximum. So dbamp(1) -> 0 and dbamp(0.5) -> -6.020600.
dbfsamp returns the decibel equivalent of the amplitude value set by the 0dbfs statement. So dbfsamp(10) is 20.000002 for 0dbfs=0 but -70.308998 for 0dbfs=32768. -
Scaling
Scaling of signals from an input range to an output range, like the "scale" object in Max/MSP, is not implemented in Csound, because it is a rather simple calculation. It is available as User Defined Opcode: Scali (i-rate), Scalk (k-rate) or Scala (a-rate).
-
PYTHON AND SYSTEM
-
PYTHON OPCODES
pyinit initializes the Python interpreter.
pyrun runs a Python statement or block of statements.
pyexec executes a script from a file at k-time, i-time or if a trigger has been received.
pycall invokes the specified Python callable at k-time or i-time.
pyeval evaluates a generic Python expression and stores the result in a Csound k- or i-variable, with optional trigger.
pyassign assigns the value of the given Csound variable to a Python variable possibly destroying its previous content.
-
SYSTEM OPCODES
getcfg returns various Csound configuration settings as a string at init time.
system / system_i call an external program via the system call.
PLUGINS
-
PLUGIN HOSTING
-
LADSPA
dssiinit loads a plugin.
dssiactivate activates or deactivates a plugin if it has this facility.
dssilist lists all available plugins found in the LADSPA_PATH and DSSI_PATH global variables.
dssiaudio processes audio using a plugin.
dssictls sends control information to a plugin's control port.
-
VST
vstinit loads a plugin.
vstaudio / vstaudiog return a plugin's output.
vstmidiout sends midi data to a plugin.
vstparamset / vstparamget sends and receives automation data to and from the plugin.
vstnote sends a midi note with a definite duration.
vstinfo outputs the parameter and program names for a plugin.
vstbankload loads an .fxb bank.
vstprogset sets the program in a .fxb bank.
vstedit opens the GUI editor for the plugin, when available.
-
APPENDIX
METHODS OF WRITING CSOUND SCORES
Although the use of Csound real-time has become more prevalent and arguably more important whilst the use if the score has diminished and become less important, composing using score events within the Csound score remains an important bedrock to working with Csound. There are many methods for writing Csound score several of which are covered here; starting with the classical method of writing scores by hand, then with the definition of a user-defined score language, and concluding several external Csound score generating programs.
Writing Score by Hand
In Csound's original incarnation the orchestra and score existed as separate text files. This arrangement existed partly in an attempt to appeal to composers who had come from a background of writing for conventional instruments by providing a more familiar paradigm. The three unavoidable attributes of a note event - which instrument plays it, when, and for how long - were hardwired into the structure of a note event through its first three attributes or 'p-fields'. All additional attributes (p4 and beyond), for example: dynamic, pitch, timbre, were left to the discretion of the composer, much as they would be when writing for conventional instruments. It is often overlooked that when writing score events in Csound we define start times and durations in 'beats'. It just so happens that 1 beat defaults to a duration of 1 second leading to the consequence that many Csound users spend years thinking that they are specifying note events in terms of seconds rather than beats. This default setting can easily be modified and manipulated as shown later on.
The most basic score event as described above might be something like this:
i 1 0 5
which would demand that instrument number '1' play a note at time zero (beats) for 5 beats. After time of constructing a score in this manner it quickly becomes apparent that certain patterns and repetitions recur. Frequently a single instrument will be called repeatedly to play the notes that form a longer phrase therefore diminishing the worth of repeatedly typing the same instrument number for p1, an instrument may play a long sequence of notes of the same duration as in a phrase of running semiquavers rendering the task of inputting the same value for p3 over and over again slightly tedious and often a note will follow on immediately after the previous one as in a legato phrase intimating that the p2 start-time of that note might better be derived from the duration and start-time of the previous note by the computer than to be figured out by the composer. Inevitably short-cuts were added to the syntax to simplify these kinds of tasks:
i 1 0 1 60 i 1 1 1 61 i 1 2 1 62 i 1 3 1 63 i 1 4 1 64
could now be expressed as:
i 1 0 1 60 i . + 1 > i . + 1 > i . + 1 > i . + 1 64
where '.' would indicate that that p-field would reuse the same p-field value from the previous score event, where '+', unique for p2, would indicate that the start time would follow on immediately after the previous note had ended and '>' would create a linear ramp from the first explicitly defined value (60) to the next explicitly defined value (64) in that p-field column (p4).
A more recent refinement of the p2 shortcut allows for staccato notes where the rhythm and timing remain unaffected. Each note lasts for 1/10 of a beat and each follows one second after the previous.
i 1 0 .1 60 i . ^+1 . > i . ^+1 . > i . ^+1 . > i . ^+1 . 64
The benefits offered by these short cuts quickly becomes apparent when working on longer scores. In particular the editing of critical values once, rather than many times is soon appreciated.
Taking a step further back, a myriad of score tools, mostly also identified by a single letter, exist to manipulate entire sections of score. As previously mentioned Csound defaults to giving each beat a duration of 1 second which corresponds to this 't' statement at the beginning of a score:
t 0 60
"At time (beat) zero set tempo to 60 beats per minute"; but this could easily be anything else or evena string of tempo change events following the format of a linsegb statement.
t 0 120 5 120 5 90 10 60
This time tempo begins at 120bpm and remains steady until the 5th beat, whereupon there is an immediate change to 90bpm; thereafter the tempo declines in linear fashion until the 10th beat when the tempo has reached 60bpm.
'm' statements allow us to define sections of the score that might be repeated ('s' statements marking the end of that section). 'n' statements referencing the name given to the original 'm' statement via their first parameter field will call for a repetition of that section.
m verse i 1 0 1 60 i . ^+1 . > i . ^+1 . > i . ^+1 . > i . ^+1 . 64 s n verse n verse n verse
Here a 'verse' section is first defined using an 'm' section (the section is also played at this stage). 's' marks the end of the section definition and 'n' recalls this section three more times.
Just a selection of the techniques and shortcuts available for hand-writing scores have been introduced here (refer to the Csound Reference Manual for a more encyclopedic overview). It has hopefully become clear however that with a full knowledge and implementation of these techniques the user can adeptly and efficiently write and manipulate scores by hand.
Extension of the Score Language: bin="..."
It is possible to pass the score as written through a pre-processor before it is used by Csound to play notes. instead it can be first interpretted by a binary (application), which produces a usual csound score as a result. This is done by the statement bin="..." in the <CsScore> tag. What happens?
- If just a binary is specified, this binary is called and two files are passed to it:
- A copy of the user written score. This file has the suffix .ext
- An empty file which will be read after the interpretation by Csound. This file has the usual score suffix .sco
- If a binary and a script is specified, the binary calls the script and passes the two files to the script.
If you have Python installed on your computer, you should be able to run the following examples. They do actually nothing but print the arguments (= file names).
Calling a binary without a script
EXAMPLE Score_methods_01.csd
<CsoundSynthesizer> <CsInstruments> instr 1 endin </CsInstruments> <CsScore bin="python"> from sys import argv print "File to read = '%s'" % argv[0] print "File to write = '%s'" % argv[1] </CsScore> </CsoundSynthesizer>
When you execute this .csd file in the terminal, your output should include something like this:
File to read = '/tmp/csound-idWDwO.ext'
File to write = '/tmp/csound-EdvgYC.sco'
And there should be a complaint because the empty .sco file has not been written:
cannot open scorefile /tmp/csound-EdvgYC.sco
Calling a binary and a script
To test this, first save this file as print.py in the same folder where your .csd examples are:
from sys import argv print "Script = '%s'" % argv[0] print "File to read = '%s'" % argv[1] print "File to write = '%s'" % argv[2]
Then run this csd:
EXAMPLE Score_methods_02.csd
<CsoundSynthesizer> <CsInstruments> instr 1 endin </CsInstruments> <CsScore bin="python print.py"> </CsScore> </CsoundSynthesizer>
The output should include these lines:
Script = 'print.py'
File to read = '/tmp/csound-jwZ9Uy.ext'
File to write = '/tmp/csound-NbMTfJ.sco'
And again a complaint about the invalid score file:
cannot open scorefile /tmp/csound-NbMTfJ.sco
Csbeats
As an alternative to the classical Csound score, Csbeats is included with Csound. This is a domain specific language tailored to the concepts of beats, rhythm and standard western notation. To use Csbeat, specify "csbeats" as the CsScore bin option in a Csound unified score file.
<CsScore bin="csbeats">
For more information, refer to the Csound Manual. Csbeats is written by Brian Baugn.
Scripting Language Examples
The following script uses a perl script to allow seeding options in the score. A random seed can be set as a comment; like ";;SEED 123". If no seed has been set, the current system clock is used. So there will be a different value for the first three random statements, while the last two statements will always generate the same values.
EXAMPLE Score_methods_03.csd
<CsoundSynthesizer>
<CsInstruments>
;example by tito latini
instr 1
prints "amp = %f, freq = %f\n", p4, p5;
endin
</CsInstruments>
<CsScore bin="perl cs_sco_rand.pl">
i1 0 .01 rand() [200 + rand(30)]
i1 + . rand() [400 + rand(80)]
i1 + . rand() [600 + rand(160)]
;; SEED 123
i1 + . rand() [750 + rand(200)]
i1 + . rand() [210 + rand(20)]
e
</CsScore>
</CsoundSynthesizer>
# cs_sco_rand.pl
my ($in, $out) = @ARGV;
open(EXT, "<", $in);
open(SCO, ">", $out);
while (<EXT>) {
s/SEED\s+(\d+)/srand($1);$&/e;
s/rand\(\d*\)/eval $&/ge;
print SCO;
}
Pysco
Pysco is a modular Csound score environment for event generation, event processing, and the fashioning musical structures in time. Pysco is non-imposing and does not force composers into any one particular compositional model; Composers design their own score frameworks by importing from existing Python libraries, or fabricate their own functions as needed. It fully supports the existing classical Csound score, and runs inside a unified CSD file.
Pysco is designed to be a giant leap forward from the classical Csound score by leveraging Python, a highly extensible general-purpose scripting language. While the classical Csound score does feature a small handful of score tricks, it lacks common computer programming paradigms, offering little in terms of alleviating the tedious process of writing scores by hand. Python plus the Pysco interface transforms the limited classical score into highly flexible and modular text-based compositional environment.
Transitioning away from the Classical Csound Score
Composers concerned about transitioning from the classical Csound score into this new environment should fear not. Only two changes are necessary to get started. First, the optional bin argument for the CsScore tag needs to specify "python pysco.py" . Second, all existing classical Csound score code works when placed inside the score() function.
<CsScore bin="python pysco.py">
score('''
f 1 0 8192 10 1
t 0 144
i 1 0.0 1.0 0.7 8.02
i 1 1.0 1.5 0.4 8.05
i 1 2.5 0.5 0.3 8.09
i 1 3.0 1.0 0.4 9.00
''')
</CsScore>
Boiler plate code that is often associated with scripting and scoring, such as file management and string concatenation, has been conveniently factored out.
The last step in transitioning is to learn a few of Python or Pysco features. While Pysco and Python offers an incredibly vast set of tools and features, one can supercharge their scores with only a small handful.
Managing Time with the cue()
The cue() object is Pysco context manager for controlling and manipulating time in a score. Time is a fundamental concept in music, and the cue() object elevates the role of time to that of other control such as if and for statements, synthesizing time into the form of the code.
In the classical Csound score model, there is only the concept of beats. This forces composers to place events into the global timeline, which requires an extra added incovenience of calculating start times for individual events. Consider the following code in which measure 1 starts at time 0.0 and measure 2 starts at time 4.0.
; Measure 1 i 1 0.0 1.0 0.7 8.02 i 1 1.0 1.5 0.4 8.05 i 1 2.5 0.5 0.3 8.09 i 1 3.0 1.0 0.4 9.00 ; Measure 2 i 1 4.0 1.0 0.7 8.07 i 1 5.0 1.5 0.4 8.10 i 1 6.5 0.5 0.3 9.02 i 1 7.0 1.0 0.4 9.07
In an ideal situation, the start times for each measure would be normalized to zero, allowing composers to think local to the current measure rather than the global timeline. This is the role of Pysco's cue() context manager. The same two measures in Pysco are rewritten as follows:
# Measure 1
with cue(0):
score('''
i 1 0.0 1.0 0.7 8.02
i 1 1.0 1.5 0.4 8.05
i 1 2.5 0.5 0.3 8.09
i 1 3.0 1.0 0.4 9.00
''')
# Measure 2
with cue(4):
score('''
i 1 0.0 1.0 0.7 8.07
i 1 1.0 1.5 0.4 8.10
i 1 2.5 0.5 0.3 9.02
i 1 3.0 1.0 0.4 9.07
''')
The start of measure 2 is now 0.0, as opposed to 4.0 in the classical score environment. The physical layout of these time-based block structure also adds visual cues for the composer, as indentation and "with cue()" statements adds clarity when scanning a score for a particular event.
Moving events in time, regardless of how many there are, is nearly effortless. In the classical score, this often involves manually recalculating entire columns of start times. Since the cue() supports nesting, it's possible and rather quite easy, to move these two measures any where in the score with a new "with cue()" statement.
# Movement 2
with cue(330):
# Measure 1
with cue(0):
i 1 0.0 1.0 0.7 8.02
i 1 1.0 1.5 0.4 8.05
i 1 2.5 0.5 0.3 8.09
i 1 3.0 1.0 0.4 9.00
#Measure 2
with cue(4):
i 1 0.0 1.0 0.7 8.07
i 1 1.0 1.5 0.4 8.10
i 1 2.5 0.5 0.3 9.02
i 1 3.0 1.0 0.4 9.07
These two measures now start at beat 330 in the piece. With the exception of adding an extra level of indentation, the score code for these two measures are unchanged.
Generating Events
Pysco includes two functions for generating a Csound score event. The score() function simply accepts any and all classical Csound score events as a string. The second is event_i(), which generates a properly formatted Csound score event. Take the following Pysco event for example:
event_i(1, 0, 1.5, 0.707 8.02)
The event_i() function transforms the input, outputting the following Csound score code:
i 1 0 1.5 0.707 8.02
These event score functions combined with Python's extensive set of features aid in generating multiple events. The following example uses three of these features: the for statement, range(), and random().
from random import random
score('t 0 160')
for time in range(8):
with cue(time):
frequency = 100 + random() * 900
event_i(1, 0, 1, 0.707, frequency)
Python's for statement combined with range() loops through the proceeding code block eight times by iterating through the list of values created with the range() function. The list generated by range(8) is:
[0, 1, 2, 3, 4, 5, 6, 7]
As the script iterates through the list, variable time assumes the next value in the list; The time variable is also the start time of each event. A hint of algorithmic flair is added by importing the random() function from Python's random library and using it to create a random frequency between 100 and 1000 Hz. The script produces this classical Csound score:
t 0 160 i 1 0 1 0.707 211.936363038 i 1 1 1 0.707 206.021046104 i 1 2 1 0.707 587.07781543 i 1 3 1 0.707 265.13585797 i 1 4 1 0.707 124.548796225 i 1 5 1 0.707 288.184408335 i 1 6 1 0.707 396.36805871 i 1 7 1 0.707 859.030151952
Processing Events
Pysco includes two functions for processing score event data called p_callback() and pmap(). The p_callback() is a pre-processor that changes event data before it's inserted into the score object while pmap() is a post-processor that transforms event data that already exists in the score.
p_callback(event_type, instr_number, pfield, function, *args) pmap(event_type, instr_number, pfield, function, *args)
The following examples demonstrates a use case for both functions. The p_callback() function pre-processes all the values in the pfield 5 column for instrument 1 from conventional notation (D5, G4, A4, etc) to hertz. The pmap() post-processes all pfield 4 values for instrument 1, converting from decibels to standard amplitudes.
p_callback('i', 1, 5, conv_to_hz)
score('''
t 0 120
i 1 0 0.5 -3 D5
i 1 + . . G4
i 1 + . . A4
i 1 + . . B4
i 1 + . . C5
i 1 + . . A4
i 1 + . . B4
i 1 + . . G5
''')
pmap('i', 1, 4, dB)
The final output is:
f 1 0 8192 10 1 t 0 120 i 1 0 0.5 0.707945784384 587.329535835 i 1 + . . 391.995435982 i 1 + . . 440.0 i 1 + . . 493.883301256 i 1 + . . 523.251130601 i 1 + . . 440.0 i 1 + . . 493.883301256 i 1 + . . 783.990871963
- www.python.org
- In some linux distributions (archlinux for example), the default python is python3. In that case, one should explicitly call python2 with the line: "python2 pysco"
CMask
CMask is an application that produces score files for Csound, i.e. lists of notes or rather events. Its main application is the generation of events to create a texture or granular sounds. The program takes a parameter file as input and makes a score file that can be used immediately with Csound.
The basic concept in CMask is the tendency mask. This is an area that is limited by 2 time variant boundaries. These area describes a space of possible values for a score parameter, for example amplitude, pitch, pan, duration etc. For every parameter of an event (a note statement pfield in Csound) a random value will be selected from the range that is valid at this time.
There are also other means in CMask for the parameter generation, for example cyclic lists, oscillators, polygons and random walks. Each parameter of an event can be generated by a different method. A set of notes / events generated by a set of methods lasting for a certain time span is called a field.
A CMask example: creation of a dynamic texture
{ f1 0 8193 10 1 ;sine wave } f 0 20 ;field duration: 20 secs p1 const 1 p2 ;decreasing density rnd uni ;from .03 - .08 sec to .5 - 1 sec mask [.03 .5 ipl 3] [.08 1 ipl 3] map 1 prec 2 p3 ;increasing duration rnd uni mask [.2 3 ipl 1] [.4 5 ipl 1] prec 2 p4 ;narrowing frequency grid rnd uni mask [3000 90 ipl 1] [5000 150 ipl 1] map 1 quant [400 50] .95 prec 2 p5 ;FM index gets higher from 2-4 to 4-7 rnd uni mask [2 4] [4 7] prec 2 p6 range 0 1 ;panorama position uniform distributed prec 2 ;between left and right
The output is:
f1 0 8193 10 1 ;sine wave ; ------- begin of field 1 --- seconds: 0.00 - 20.00 -------- ;ins time dur p4 p5 p6 i1 0 0.37 3205.55 3.57 0.8 i1 0.07 0.24 3190.83 3.55 0.28 i1 0.12 0.3 3589.39 2.74 0.51 i1 0.2 0.38 3576.81 3.46 0.14 i1 0.25 0.2 3158.89 2.3 0.8 i1 0.28 0.28 2775.01 2.25 1 ........ ........ ........ i1 18.71 4.32 145.64 5.75 0.27 i1 19.12 3.27 129.68 5.27 0.3 i1 19.69 4.62 110.64 6.87 0.65 ; ------- end of field 1 --- number of events: 241 -------
Cmask can be downloaded for MacOS9, Win, Linux (by André Bartetzki) and is ported to OSX(by Anthony Kozar).
nGen
nGen is a free multi-platform generation tool for creating Csound event-lists (score files) and standard MIDI files. It is written in C and runs on a variety of platforms (version 2.1.2 is currently available for Macintosh OS 10.5 and above, Linux Intel and Windows 7+). All versions run in the UNIX command-line style (at a command-line shell prompt). nGen was designed and written by composer Mikel Kuehn and was inspired in part by the basic syntax of Aleck Brinkman's Score11 note list preprocessor (Score11 is available for Linux Intel from the Eastman Computer Music Center) and Leland Smith's Score program.
nGen will allow you to do several things with ease that are either difficult or not possible using Csound and/or MIDI sequencing programs; nGen is a powerful front-end for creating Csound score-files and basic standard MIDI files. Some of the basic strengths of nGen are:
- Event-based granular textures can be generated quickly. Huge streams of values can be generated with specific random-number distributions (e.g., Gaussian, flat, beta, exponential, etc.).
- Note-names and rhythms can be entered in intuitive formats (e.g., pitches: C4, Df3; rhythms: 4, 8, 16, 32).
- "Chords" can be specified as a single unit (e.g., C4:Df:E:Fs). Textual and numeric macros are available.
Additionally, nGen supplies a host of conversion routines that allow p-field data to be converted to different formats in the resulting Csound score file (e.g., octave.pitch-class can be formatted to Hz values, etc.). A variety of formatting routines are also supplied (such as the ability to output floating-point numbers with a certain precision width).
nGen is a portable text-based application. It runs on most platforms (Windows, Mac, Linux, Irix, UNIX, etc.) and allows for macro- and micro-level generation of event-list data by providing many dynamic functions for dealing with statistical generation (such as interpolation between values over the course of many events, varieties of pseudo-random data generation, p-field extraction and filtering, 1/f data, the use of "sets" of values, etc.) as well as special modes of input (such as note-name/octave-number, reciprocal duration code, etc.). Its memory allocation is dynamic, making it useful for macro-level control over huge score-files. In addition, nGen contains a flexible text-based macro pre-processor (identical to that found in recent versions of Csound), numeric macros and expressions, and also allows for many varieties of data conversion and special output formatting. nGen is command-line based and accepts an ASCII formatted text-file which is expanded into a Csound score-file or a standard MIDI file. It is easy to use and is extremely flexible making it suitable for use by those not experienced with high-level computer programming languages.
An example of simple granular synthesis with wave forms
;These lines go directly to the output file
>f1 0 16384 10 1 ;sine wave
>f2 0 16384 10 1 0 .5 0 .25 0 .125 0 .0625 ;odd partials (dec.)
>f3 0 16384 10 1 .5 .25 .125 .0625 ;all w/ decreasing strength
>f4 0 16384 10 1 1 1 1 1 ;pulse
>f5 0 16384 10 1 0 1 0 1 ;odd
>f82 0 16385 20 2 1 ;grain envelope
#define MAX #16000# ;a macro for the maximum amplitude
i1 = 7 0 10 {
p2 .01 ;intervalic start time
/* The duration of each event slowly changes over time starting at 20x the
initial start time interval to 1x the ending start-time interval. The "T"
variable is used to control the duration of both move statements (50% of the
entire i-block duration). */
p3 mo(T*.5 1. 20 1) mo(T*.5 1. 1 10)
/* Amplitude gets greater in the center to compensate for shorter grains the
MAX macro (see above) is used to set the high range anchor. */
p4 rd(.1) mo(T*.5, 1. E 0 $MAX) mo(T*.5 1. E $MAX 0)
/* Frequency: moves logarithmically from 3000 to a range between 100 and 200
then exponentially up to a range between 1000 and 4000. The "T" variable
is again used to specify a percentage of the iblock's total duration. If
you try to compile this as a MIDI file, all of the Herz values will turn
into MIDI note numbers through VALUE % 128 -- rapidly skimming over the
entire keyboard... */
p5 rd (0) mo(T*.4 1. l 3000 [100 200]) mo(T*.6 1. e [100 200] [1000 4000])
/* Spatial placement: 25% hard-left 25% hard-right 50% a Gaussian value
(near the middle). */
p6(re2) ra(10 .25 0 .25 1 .5 [g 0 1])
p7(in) se(T 1. [1 2 3 4 5]) ;select different wave-form function #s
}
The output is:
f1 0 16384 10 1 ;sine wave f2 0 16384 10 1 0 .5 0 .25 0 .125 0 .0625 ;odd partials (dec.) f3 0 16384 10 1 .5 .25 .125 .0625 ;all w/ decreasing strength f4 0 16384 10 1 1 1 1 1 ;pulse f5 0 16384 10 1 0 1 0 1 ;odd f82 0 16385 20 2 1 ;grain envelope ;I-block #1 (i1): i1 0.000 0.200 0.000 3000.000 0.00 3 i1 0.010 0.200 0.063 2673.011 0.79 3 i1 0.020 0.199 0.253 2468.545 1.00 2 i1 0.030 0.199 0.553 2329.545 1.00 5 i1 0.040 0.198 1.033 2223.527 1.00 2 i1 0.050 0.198 1.550 2160.397 0.50 4 ........ ........ ........ i1 9.970 0.100 127.785 2342.706 0.48 1 i1 9.980 0.100 64.851 3200.637 1.00 1 i1 9.990 0.100 0.000 3847.285 1.00 2 e
nGen for Mac, Windows and Linux can be downloaded here
AthenaCL
The athenaCL system is a software tool for creating musical structures. Music is rendered as a polyphonic event list, or an EventSequence object. This EventSequence can be converted into diverse forms, or OutputFormats, including scores for the Csound synthesis language, Musical Instrument Digital Interface (MIDI) files, and other specialized formats. Within athenaCL, Orchestra and Instrument models provide control of and integration with diverse OutputFormats. Orchestra models may include complete specification, at the code level, of external sound sources that are created in the process of OutputFormat generation.
The athenaCL system features specialized objects for creating and manipulating pitch structures, including the Pitch, the Multiset (a collection of Pitches), and the Path (a collection of Multisets). Paths define reusable pitch groups. When used as a compositional resource, a Path is interpreted by a Texture object (described below).
The athenaCL system features three levels of algorithmic design. The first two levels are provided by the ParameterObject and the Texture. The ParameterObject is a model of a low-level one-dimensional parameter generator and transformer. The Texture is a model of a multi-dimensional generative musical part. A Texture is controlled and configured by numerous embedded ParameterObjects. Each ParameterObject is assigned to either event parameters, such as amplitude and rhythm, or Texture configuration parameters. The Texture interprets ParameterObject values to create EventSequences. The number of ParameterObjects in a Texture, as well as their function and interaction, is determined by the Texture's parent type (TextureModule) and Instrument model. Each Texture is an instance of a TextureModule. TextureModules encode diverse approaches to multi-dimensional algorithmic generation. The TextureModule manages the deployment and interaction of lower level ParameterObjects, as well as linear or non-linear event generation. Specialized TextureModules may be designed to create a wide variety of musical structures.
The third layer of algorithmic design is provided by the Clone, a model of the multi-dimensional transformative part. The Clone transforms EventSequences generated by a Texture. Similar to Textures, Clones are controlled and configured by numerous embedded ParameterObjects.
Each Texture and Clone creates a collection of Events. Each Event is a rich data representation that includes detailed timing, pitch, rhythm, and parameter data. Events are stored in EventSequence objects. The collection all Texture and Clone EventSequences is the complete output of athenaCL. These EventSequences are transformed into various OutputFormats for compositional deployment.
AthenaCL can be downloaded here.
Common Music
Common Music is a music composition system that transforms high-level algorithmic representations of musical processes and structure into a variety of control protocols for sound synthesis and display. It generates musical output via MIDI, OSC, CLM, FOMUS and CSOUND. Its main user application is Grace (Graphical Realtime Algorithmic Composition Environment) a drag-and-drop, cross-platform app implemented in JUCE (C++) and S7 Scheme. In Grace musical algorithms can run in real time, or faster-than-real time when doing file-based composition. Grace provides two coding languages for designing musical algorithms: S7 Scheme, and SAL, an easy-to-learn but expressive algol-like language.
Some of the features:
- Runs on Mac, Windows and Linux
- Two coding languages for designing algorithms: S7 Scheme and SAL (an easy-to-learn alternate)
- Data visualization
Common Music 3 can be downloaded here.
GLOSSARY
control cycle, control period or k-loop is a pass during the performance of an instrument, in which all k- and a-variables are renewed. The time for one control cycle is measured in samples and determined by the ksmps constant in the orchestra header. If your sample rate is 44100 and your ksmps value is 10, the time for one control cycle is 1/4410 = 0.000227 seconds. See the chapter about Initialization And Performance Pass for more information.
control rate or k-rate (kr) is the number of control cycles per second. It can be calculated as the relationship of the sample rate sr and the number of samples in one control period ksmps. If your sample rate is 44100 and your ksmps value is 10, your control rate is 4410, so you have 4410 control cycles per second.
dummy f-statement see f-statement
f-statement or function table statement is a score line which starts with a "f" and generates a function table. See the chapter about function tables for more information. A dummy f-statement is a statement like "f 0 3600" which looks like a function table statement, but instead of generating any table, it serves just for running Csound for a certain time (here 3600 seconds = 1 hour).
FFT Fast Fourier Transform is a system whereby audio data is stored or represented in the frequency domain as opposed to the time domain as amplitude values as is more typical. Working with FFT data facilitates transformations and manipulations that are not possible, or are at least more difficult, with audio data stored in other formats.
GEN rountine a GEN (generation) routine is a mechanism within Csound used to create function tables of data that will be held in RAM for all or part of the performance. A GEN routine could be a waveform, a stored sound sample, a list of explicitly defined number such as tunings for a special musical scale or an amplitude envelope. In the past function tables could only be created only in the Csound score but now they can also be created (and deleted and over-written) within the orchestra.
GUI Graphical User Interface refers to a system of on-screen sliders, buttons etc. used to interact with Csound, normally in realtime.
i-time or init-time or i-rate signify the time in which all the variables starting with an "i" get their values. These values are just given once for an instrument call. See the chapter about Initialization And Performance Pass for more information.
k-loop see control cycle
k-time is the time during the performance of an instrument, after the initialization. Variables starting with a "k" can alter their values in each ->control cycle. See the chapter about Initialization And Performance Pass for more information.
k-rate see control rate
opcode the code word of a basic building block with which Csound code is written. As well as the opcode code word an opcode will commonly provide output arguments (variables), listed to the left of the opcode, and input arguments (variables). listed to the right of the opcode. An opcode is equivalent to a 'ugen' (unit generator) in other languages.
orchestra as in the Csound orchestra, is the section of Csound code where traditionally the instruments are written. In the past the 'orchestra' was one of two text files along with the 'score' that were needed to run Csound. Most people nowadays combine these two sections, along with other optional sections in a .csd (unified) Csound file. The orchestra will also normally contain header statements which will define global aspects of the Csound performance such as sampling rate.
p-field a 'p' (parameter) field normally refers to a value contained within the list of values after an event item with the Csound score.
performance pass see control cycle
score as in the Csound score, is the section of Csound code where note events are written that will instruct instruments within the Csound orchestra to play. The score can also contain function tables. In the past the 'score' was one of two text files along with the 'orchestra' that were needed to run Csound. Most people nowadays combine these two sections, along with other optional sections in a .csd (unified) Csound file.
time stretching can be done in various ways in Csound. See sndwarp, waveset, pvstanal mincer, pvsfread, pvsdiskin and the Granular Synthesis opcodes.
widget normally refers to some sort of standard GUI element such as a slider or a button. GUI widgets normally permit some user modifications such as size, positioning colours etc. A variety options are available for the creation of widgets usable by Csound, from it own built-in FLTK widgets to those provided by front-ends such as CsoundQT, Cabbage and Blue.
LINKS
Downloads
Csound FLOSS Manual Files: http://files.csound-tutorial.net/floss_manual/
Csound: http://csound.com/download.html
Csound source code: http://github.com/csound/csound
Csound's User Defined Opcodes: http://www.csounds.com/udo/ and http://github.com/csudo/csudo
CsoundQt: http://github.com/CsoundQt/CsoundQt/releases
WinXound: http://mnt.conts.it/winxound/
Blue: http://blue.kunstmusik.com/
Cabbage: http://cabbageaudio.com/
Most recent (unstable/develop) Csound installer: https://ci.appveyor.com/project/csound/csound/build/artifacts
Most recent (unstable/develop) CsoundQt version: https://github.com/CsoundQt/CsoundQt/releases
Community
Csound's info page on github is a good collection of links and basic infos.
The Csound Journal is a main source for different aspects of working with Csound.
Mailing Lists and Bug Tracker
Main place for questions and informations is the Csound Mailing List. To subscribe to the Csound User Discussion List, go to https://listserv.heanet.ie/cgi-bin/wa?A0=CSOUND. After subscribing, put questions at csound@listserv.heanet.ie. You can search in the list archive at nabble.com.
To subscribe to the CsoundQt User Discussion List, go to https://lists.sourceforge.net/lists/listinfo/qutecsound-users. You can browse the list archive here.
Csound Developer Discussions: https://listserv.heanet.ie/cgi-bin/wa?A0=CSOUND-DEV
Blue: http://sourceforge.net/mail/?group_id=74382
Cabbage http://forum.cabbageaudio.com/
Please report any bug you experienced in Csound at http://github.com/csound/csound/issues, and a CsoundQt related bug at http://sourceforge.net/tracker/?func=browse&group_id=227265&atid=1070588. Every bug report is an important contribution.
Tutorials
A Beginning Tutorial is a short introduction from Barry Vercoe, the "father of Csound".
An Instrument Design TOOTorial by Richard Boulanger (1991) is another classical introduction, still very worth to read.
Introduction to Sound Design in Csound also by Richard Boulanger, is the first chapter of the famous Csound Book (2000).
Virtual Sound by Alessandro Cipriani and Maurizio Giri (2000)
A Csound Tutorial by Michael Gogins (2009), one of the main Csound Developers.
Video Tutorials
A playlist as overview by Alex Hofmann:
http://www.youtube.com/view_play_list?p=3EE3219702D17FD3
CsoundQt (QuteCsound)
QuteCsound: Where to start?
http://www.youtube.com/watch?v=0XcQ3ReqJTM
First instrument:
http://www.youtube.com/watch?v=P5OOyFyNaCA
Using MIDI:
http://www.youtube.com/watch?v=8zszIN_N3bQ
About configuration:
http://www.youtube.com/watch?v=KgYea5s8tFs
Presets tutorial:
http://www.youtube.com/watch?v=KKlCTxmzcS0
http://www.youtube.com/watch?v=aES-ZfanF3c
Live Events tutorial:
http://www.youtube.com/watch?v=O9WU7DzdUmE
http://www.youtube.com/watch?v=Hs3eO7o349k
http://www.youtube.com/watch?v=yUMzp6556Kw
New editing features in 0.6.0:
http://www.youtube.com/watch?v=Hk1qPlnyv88
New features in 0.7.0:
https://www.youtube.com/watch?v=iytVlxMILyw
New features in 0.9.2:
https://youtu.be/q_1SUT1wD6o
Csoundo (Csound and Processing)
http://csoundblog.com/2010/08/csound-processing-experiment-i/
Open Sound Control in Csound
http://www.youtube.com/watch?v=JX1C3TqP_9Y
Csound and Inscore
http://vimeo.com/54160283 (installation)
http://vimeo.com/54160405 (examples)
german versions:
http://vimeo.com/54159567 (installation)
http://vimeo.com/54159964 (beispiele)
Csound Conferences
See the list at http://csound.com/community.html
Example Collections
Csound Realtime Examples by Iain McCurdy is one of the most inspiring and up-to-date collections.
The Amsterdam Catalog by John-Philipp Gather is particularily interesting because of the adaption of Jean-Claude Risset's famous "Introductory Catalogue of Computer Synthesized Sounds" from 1969.
Books
The Csound Book (2000) edited by Richard Boulanger is still the compendium for anyone who really wants to go in depth with Csound.
Virtual Sound by Alessandro Cipriani and Maurizio Giri (2000)
Signale, Systeme, und Klangsysteme by Martin Neukom (2003, german) has many interesting examples in Csound.
The Audio Programming Book edited by Richard Boulanger and Victor Lazzarini (2011) is a major source with many references to Csound.
Csound Power! by Jim Aikin (2012) is a perfect up-to-date introduction for beginners.
Csound — A Sound and Music Computing System (2016) by Victor Lazzarini and others is the new Csound Book, covering all parts of the Csound audio programming language in depth.
